【徹底解説】数検1級合格へのロードマップ

本稿では，数学検定1級の取得を目指される方に向けて，試験の攻略方法をお伝えします。前半パートでは数検1級の概要と1次試験の出題傾向を体系立ててまとめ，後半パートでは2次試験の傾向と対策やおすすめの参考書を紹介します。

当サイトでは，数検1級で問われる各論を網羅的にまとめています。以下の目次ページをご参照ください。

はじめに

数学検定は数学・算数の実用的な技能を測定する記述式の検定で，日本数学検定協会が主催しています。数学領域である1級〜5級を「数学検定」と呼び，算数領域である6級〜11級，及びかず・かたち検定までを「算数検定」と呼びます。1〜5級は計算技能を問う1次試験と数理技能を問う2次試験に分かれ，両試験は同日に実施されます。どの級にも受験資格は存在せず，1級から取得することも可能です。合格後の更新という概念もなく，一度該当級の検定の合格すれば失効することはありません。本稿では，数学検定のうち1級の攻略方法についてお伝えします。

概要

概要		詳細	一言
レベル感		大学教養レベル	大学教養90%・特有問題10%
出題数	1次	7問	全問必須で解く順番も大切
	2次	2問必須＋5問中2問選択	微積/線形/微分方程式が必須になりがち
合格基準	1次	70％程度	7問中5問以上の正解が必要
	2次	60％程度	4問中2.5問以上の正解が必要
検定時間	1次	60分	確実に時間との戦い
	2次	120分	時間は余裕だが問題のチョイスが重要
検定日		A日程の年3回（4月/7月/10月）	数検1級では団体受験ができない
検定料		数検1級概要ページよりご確認ください	最近値上げ傾向にある

1次試験は60分で7題を解き切る必要があり，「計算技能」を問うだけあって時間との戦いになります。数検1級界隈では有名ですが，2次試験よりも1次試験の方が合格することが難しい試験であるとも言われてます。1次試験では計算力はもちろんのこと，問題文をパッと見て直感的に答えを概算する能力や自分の出した答えが妥当かどうかを判断するための検算能力など，60分で7題を解き切るための多角的な能力が問われます。一方，2次試験では定規・コンパス・電卓（一般的な電卓に加え関数電卓とグラフ電卓を利用可能）が持ち込み可能となっており，計算技能ではなく深い思考能力（数理技能）が問われます。定義と諸定理の正確な理解を前提にした問題が多く，数学的な背景として発展的なテーマが問われることもあります。

数検1級に合格するためには1次試験と2次試験を同日に合格する必要はなく，片方の試験に落ちたとしても後日片方の試験だけを受験することが可能です。公式ページではこの仕組みを免除申請と呼んでおり，1次試験・2次試験いずれの免除においても検定料が1,000円引きになります。

あまり知られていませんが，希望者には同日英語版での受験が可能になっています。ただし，英語版の実施がない受験日もあるため注意してください。

試験範囲

数検1級の試験範囲は概要ページに記載されています。

試験範囲とは別に，技能の概要として下記のような記述があります。

情報科学社会の発展や地球環境の保全あるいは経済活動などを自立的，協働的に推進するために必要な数学技能
1. 自然科学に密着した数学上の諸技法を駆使し，諸法則を活用することができる。
2. 抽象的な思考ができる。
3. 身の回りの事象について，数学的に推論ができる。

数検1級の概要ページより

数学検定協会としては，純粋数学への理解よりも実用上大切になる技能を問うていることが伺えます。数学検定であるのにコンピュータという試験範囲があることからも，情報科学社会における数学の位置付けを意識していることが強く伝わってきます。微積分や固有値は実用のための超基本的なツールという位置付けであり，例えば過去にはピエール=フランソワ・フェルフルストが人口増加について論じた中で出てくる微分方程式をテーマにした出題もありました。他にも，ニュートン法による数値計算やグラフ理論が問われることもありますが，共通しているのは「定義と諸定理を正確に理解して活用することができるか」です。問題演習一辺倒になってもいけないですし，教科書を読んだだけで分かった気になってもいけないのです。

傾向と対策

数検1級には明確に出題傾向があります。この傾向を掴まなければ，数学に精通している専門家であっても足元をすくわれる可能性が高いです。筆者は数検1級の過去問題集から対策本まで関連書籍を買い漁り，問われやすい知識を体形立てました。まずは1次試験の出題傾向を眺めていきましょう。

代数学

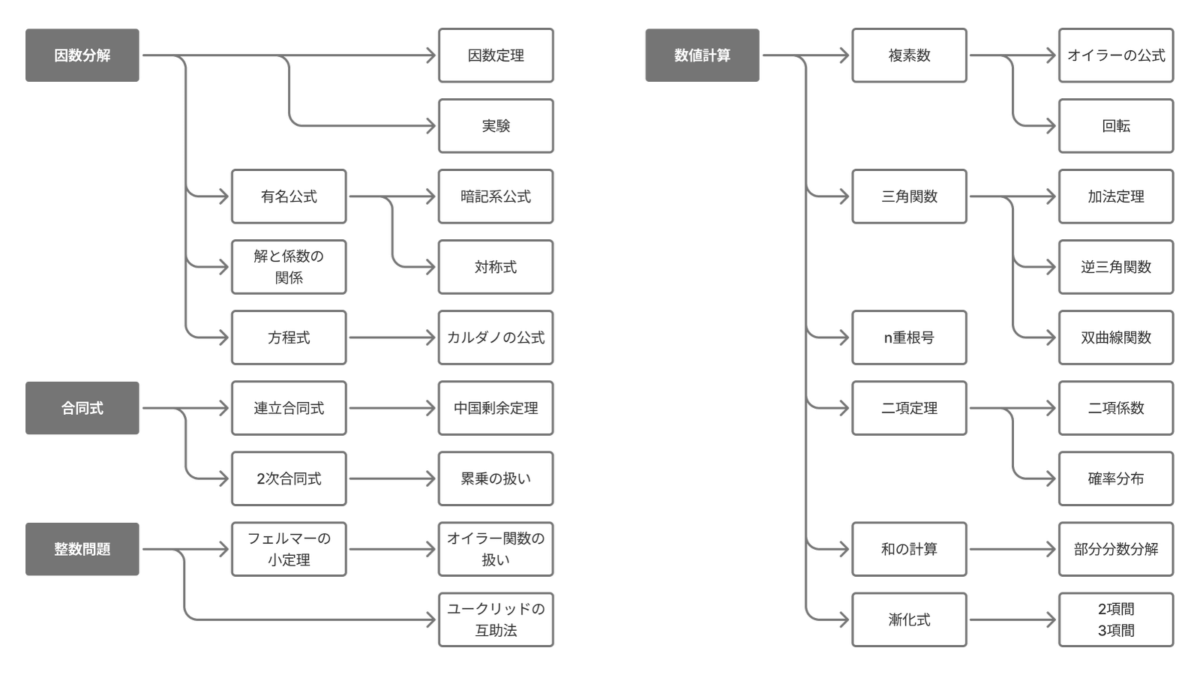
代数学は主に大問1〜2で出題されます。基本的には2問の出題となります。

因数定理を用いた因数分解は必ず押さえなければならず，因数の候補として取り得る値が「$\pm$定数項/最高次数の係数」であることを利用する問題が頻出です。他にも対称式を用いた式変形やカルダノの公式を用いた一般的な$3$次方程式の解法もよく問われます。

合同式も頻出で，特に連立一次合同式は押さえるべきでしょう。汎用的な解法として中国剰余定理を押さえておけると安心ですが，まずは法を揃えた上で合同式の性質を用いて式変形することにより$x\equiv\cdots$という形を出現させる定番の解法をマスターしましょう。

大きな数を用いた累乗の計算が問われることも多いです。これはフェルマーの小定理やオイラーの定理を利用するとうまく解くことができますが，例えば$2025$年度の出題であれば$(2000+25)^{n}$のような形で二項展開を利用しても解くことができる問題も狙われやすいです。いずれにしてもオイラーの定理を押さえておけば，まず間違いないでしょう。

数値計算系の出題はバリエーションに富んでいます。複素数を絡める問題では，オイラーの公式を用いて有名角の三角関数に帰着させる問題が頻出です。たまに幾何的に回転を伴う問題が狙われます。逆三角関数は非常によく問われ，逆三角関数の加法定理のような形や双曲線関数の計算が狙われます。二重根号を外す問題は対称式・解と係数の関係に帰着させる問題が頻出です。コンビネーション記号の和の計算は二項展開を利用しても解くことができる問題と上手く解くことができますが，たまにベータ関数などの確率分布を持ち出すとエレガントに解ける問題が出題されます。級数の計算においては，部分分数分解によりテレスコーピング和として処理する問題が頻出です。式変形の結果，漸化式の知識が必要になる問題もたまに出題されます。

Pell方程式とその解法は頻出ではないためスコープアウトしました。

線形代数学

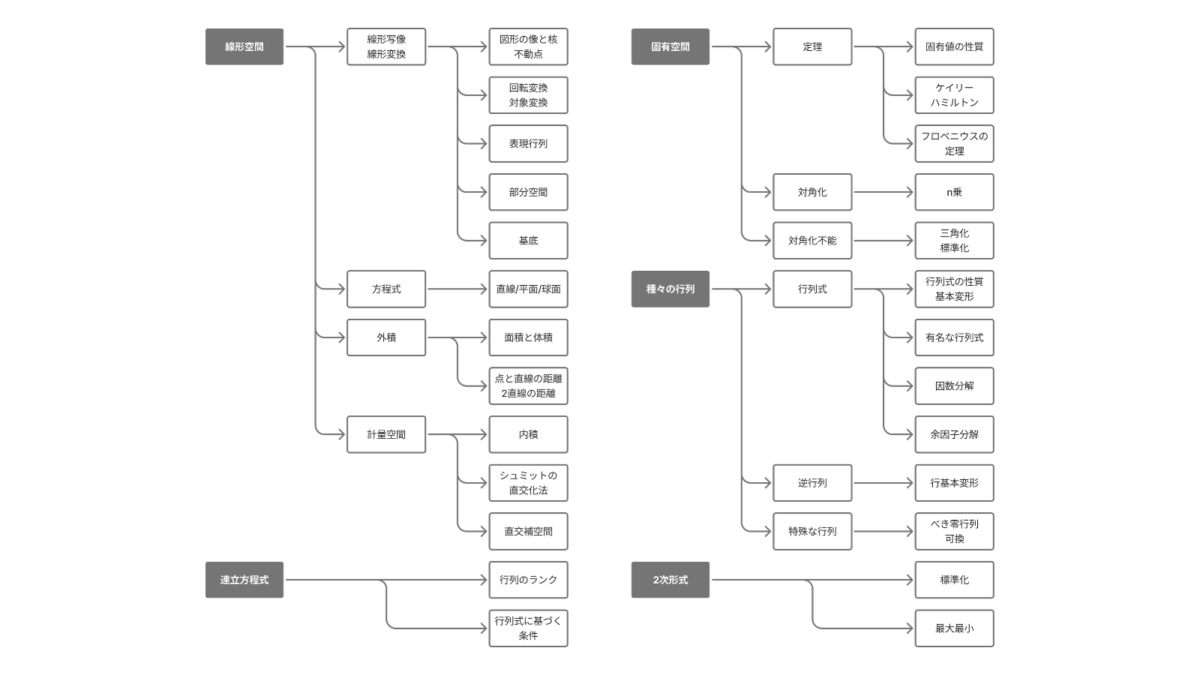
線形代数学は主に大問3〜6で出題されます。基本的には1問もしくは2問の出題となります。

線形写像や線形空間については，特に回転行列や表現行列がよく問われます。回転行列は幾何的にある点を回転させる問題として問われることが多く，表現行列は変換を表す行列$A$，変換前の基底$\vv$，変換後の基底$\vw$とおいたときに$A\vv=\vw P$と定義される$P$であると理解できているかを問う問題が頻出です。

直線・平面の方程式も超頻出です。ある直線を含む平面や点と平面の距離，ねじれの位置にある2直線の距離が特に問われやすいトピックです。直線・平面の方程式と絡めて外積の定義を性質が問われることも多く，2つの方向ベクトルに垂直なベクトルを求めるために外積を利用します。計量空間について問われることはほぼありませんが，シュミットの直交化法を用いて直交行列を作らなければ解けない問題が出題されることもあります。

複雑な連立方程式が出題されることもあります。加減法で解くこともできるのですが，1問10分未満というスピードが求められる数検1次試験においては拡大係数行列の行基本変形を用いて迅速に解くことが求められます。

固有空間については，固有値とケイリー・ハミルトンの定理がとにかく頻出です。純粋に「固有値を求めなさい」という出題になることもあれば，行列の$n$乗を求めるために固有方程式を求めてケイリー・ハミルトンの定理により次数下げを行う問題になることもあります。三角化やジョルダン標準形はほぼ問われないものと思ってよいでしょう。

行列の演算系については，行列式の計算と逆行列の導出が頻出です。行列式の計算はブロック行列の性質を利用する問題か基本変形と余因子展開を利用する流れが定番です。逆行列は掃き出し法を利用して導出するのが一番手っ取り早いでしょう。たまにべき零行列と可換行列の性質を利用して行列を二項展開する問題が問われます。2次形式を標準化する問題が出題されることもありますが，頻出ではないためそこまでアンテナを張りすぎる必要はないでしょう。

二次曲線と二次曲面は頻出ではないためスコープアウトしました。

解析学

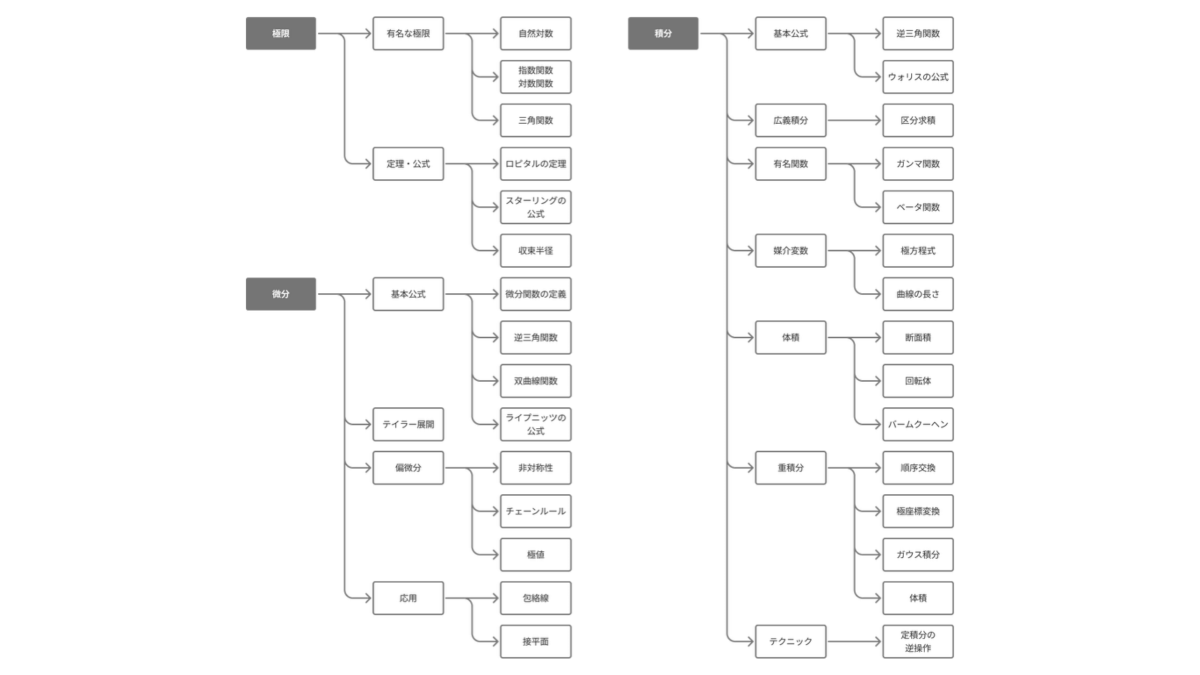
解析学は主に大問4〜7で出題されます。基本的には2問の出題となります。問7は重積分の問題か微分方程式の問題になることが多く，1次の問7で重積分が出題されれば2次の問7で微分方程式が出題され，1次の問7で微分方程式が出題されれば2次の問7で重積分が出題されるケースが多いです。

極限の問題では自然対数の定義を利用するベーシックな出題から，ロピタルの定理やスターリングの公式を利用する出題まで幅広いです。特にダランベールの公式やコーシーの公式を利用して収束半径を求める問題が頻出です。これらの判定法では端点は個別に収束判定する必要がある点に十分注意してください。

逆三角関数の微分や双曲線関数の微分が問われやすいです。それぞれ三角関数の定義と双曲線関数の定義から容易に導くことができるため，暗記に頼るよりは毎回導出した方が脳のメモリを圧迫せずに済むでしょう。シンプルな関数の積になっている関数のマクローリン展開もよく問われます。代表例は$\tan x$のマクローリン展開ですが，これは$\sin x$のマクローリン展開と$\cos x$のマクローリン展開を用いて解くことができます。たまに合成関数の偏微分や接平面が問われることがあります。

結果が逆三角関数となる不定積分も問われやすいです。これは微分とは異なり「微分したら逆三角関数になる」ことから天下り的に形を決めつけてしまう積分の手法として位置付けられます。複雑な積分計算を，ベータ関数やガンマ関数に帰着させて階乗の性質を利用する問題も出題されます。媒介変数を用いて表される関数の重積分もよく問われますが，これは本質的には「積分順序の交換と領域の作り方」「ヤコビアンの導出方法」あたりが問われる印象があります。極形式を用いて表される図形の面積はあまり出題頻度は高くありません。

重心は頻出ではないためスコープアウトしました。

確率統計

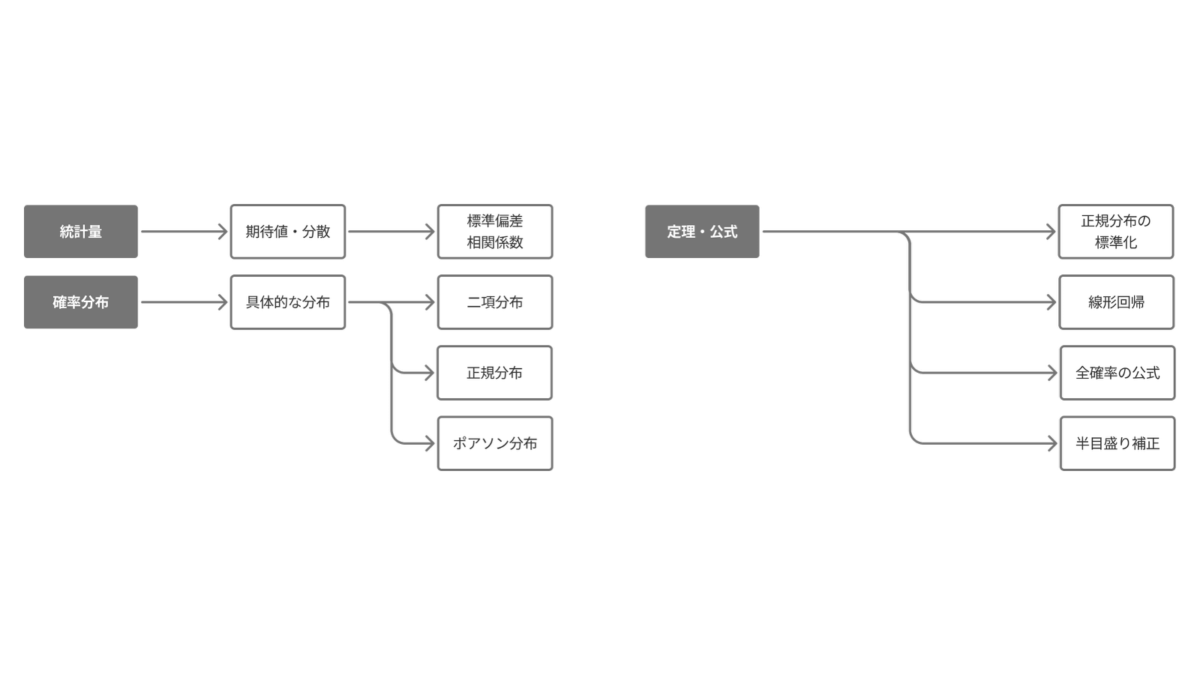
確率統計は主に大問4〜6で出題されます。基本的には1問の出題となります。

期待値や分散を定義から求める問題が超頻出です。定義域全体で積分すると$1$になることから与えられた定数を求める問題も頻出です。具体的な確率分布としては二項分布・正規分布・ポアソン分布を押さえておけばよいでしょう。たまに幾何分布が問われることもあります。線形回帰は2次試験で問われやすいですが，1次試験においては共分散や相関係数を求めさせる問題が頻出です。

微分方程式

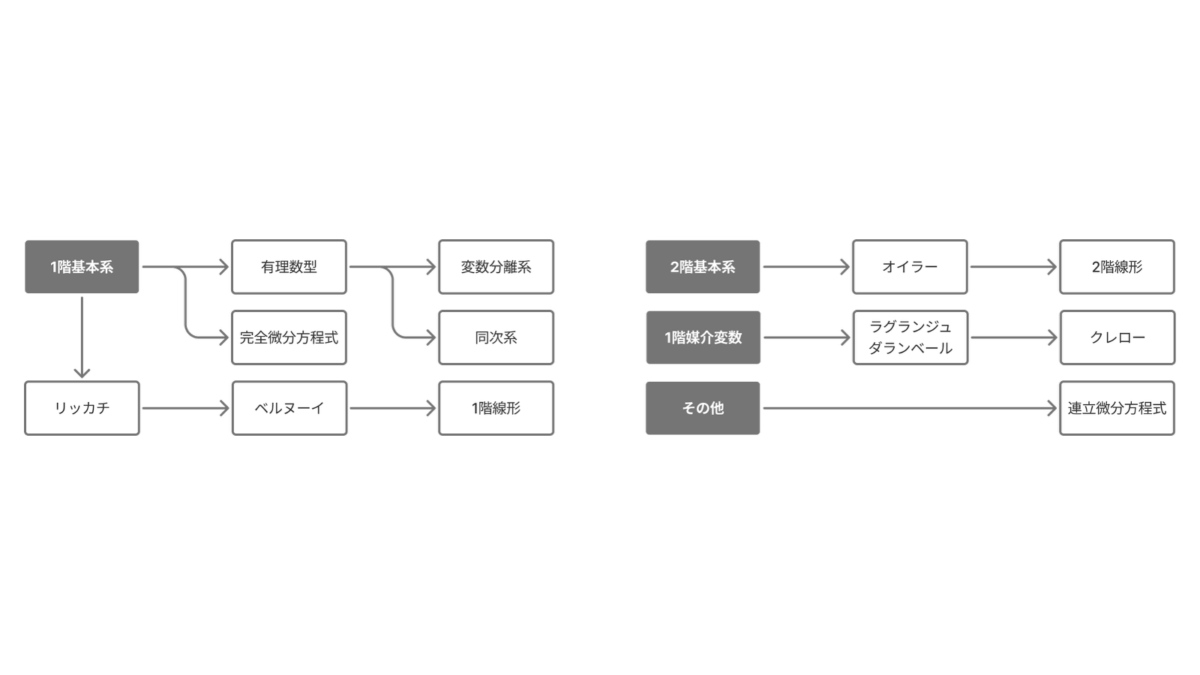
微分方程式は主に大問7で出題されます。基本的には1問の出題もしくは出題がない回もあります。上述しましたが，問7は重積分の問題か微分方程式の問題になることが多く，1次の問7で重積分が出題されれば2次の問7で微分方程式が出題され，1次の問7で微分方程式が出題されれば2次の問7で重積分が出題されるケースが多いです。

ベーシックなパターンとして変数分離系・同次系・線形微分方程式・有理関数型は非常によく問われます。非同次線形微分方程式については右辺の形はシンプルになることが多く，左辺の特性方程式の解空間とも一致しないパターンが多いでしょう。これが一致する問題は2次試験のレベルになるイメージです。和と差を取るだけで基本的な$1$元の微分方程式に帰着させられる連立微分方程式が問われることもあります。

線形微分方程式の級数解法は頻出ではないためスコープアウトしました。

おすすめ参考書

数検1級取得を目指す上では，まず大前提として高校数学はマスターしている必要があります。その上で，大学数学を始めて学ぶ方を想定しておすすめの参考書を挙げていきます。数検1級対策の参考書は大きく以下の分類に分けられます。

• 分野俯瞰型
• 科目特化型
• テクニック型
• 過去問演習型

大学数学が初めての方は分野俯瞰型の参考書で一通り全体の流れを掴むとよいでしょう。1周目は分からない箇所があっても気にせず読み進めてください。2周目はもう少し精密に読んでいきますが実際に手はまだ動かさなくてもよいです。3周目で実際に手を動かしながら証明を追ったり演習問題を解いたりしてみてください。

口うるさく言われていることですが，数学は手を動かさないと本当にできるようになりません。参考書を目で追うだけの勉強よりも，最終的には必ず手を動かすことは意識しましょう。余裕がある方は科目特化型やテクニック型で知識をチューニングし，過去問演習型の参考書を利用して「どのようなテクニックを利用してもよいので時間内に解き切る練習」をします。

分野俯瞰型

大学数学初学者が分野を俯瞰できるタイプの参考書を紹介します。

準拠テキスト

日本数学検定協会の公式HPでも紹介されている準拠テキストです。微分方程式を除きよく網羅されています。まずはこのテキストを読んでみて，各分野ごとにキャッチーな学習が必要そうと感じれば，以下で紹介する「マセマシリーズ」「弱点克服シリーズ」のいずれかを利用するとよいでしょう。

合格ナビ

分野が一通りまとまっていますが，定義や定理の細切れ紹介に終始してストーリー化されていないため，初学者という観点ではあまりおすすめできるものではありません。上で紹介した準拠テキストか，以下で紹介する「マセマシリーズ」「弱点克服シリーズ」のいずれかを利用するとよいでしょう。管理人は知識の上塗りのためにこのテキストを利用していました。

マセマシリーズ

定番のマセマシリーズです。なぜかナメられがちですが，本質的な内容をキャッチーに学ぶことができます。実際のページは少しごちゃごちゃしていて視覚的に見にくい部分もありますが，行間が詰まっていない参考書よりはマシでしょう。マセマシリーズでは解説編と演習編の両方に取り組むことをおすすめします。

弱点克服シリーズ

線形代数・微分積分・微分方程式は上で紹介した準拠テキストの作者である江川先生の著書です。準拠テキストとの親和性も高いですし，大学の定期試験対策でも重宝するシリーズになっています。

科目特化型

微分方程式は科目特化型で鍛えられるとベターです。ここで紹介している2冊はいずれも微分方程式の本質を学びやすい書籍です。「基礎解析学コース 微分方程式」はかなり薄いのでサクッと読み進められます。「微分方程式 理工学の原点」はストーリー性があって読み物として読み進められる書籍です。

明解演習シリーズは既にある程度の素養がある方に向けた分野特化型の演習書です。文章に旧字が使われているなど歴史を感じられる書籍ですが，大ロングセラーとして本質的な内容をミニマムで学ぶことができる良質な演習書です。

テクニック型

これらの3冊は数検1級対策に特化した書籍ですが，正直かなりレベルが高いです。「完全ガイド！数学検定1級 出題パターン徹底研究」と「ためせ実力！数学検定1級 実践演習」は準拠テキストの作者である中村先生の書籍ですが，数検1級の中でも難しい問題もかなり扱っており，これらの問題集から入ると数検1級が非常に高い壁に見えてしまうと思います。「数検1級をめざせ 大学初年級問題解法の手引き」は数学界では有名な一松先生による著書で，一松先生が数検1級の採点に関わっていた頃の実話を交えながら出題傾向や数学への向き合い方を記された読み物になっています。2025年6月に改装版が出版されましたが，これだけでは1級合格は難しいでしょう。これらの3冊はいずれも余裕がある方向けの書籍になっています。

過去問演習型

数検1級の過去問題集はいくつか発売されていますが，最新のものは上記の「発見」となります。全7回分の1次試験と2次試験が収録されており，解説も充実しているため必読書といってもよいでしょう。ただし，収録されている過去問は発売当時から直近の試験を連続で抜き出しているものと思われるため，過去問から厳選された良質な過去問演習を行えるとは限らない点に注意してください。

2次試験の概要と対策

2次試験では主に以下のような出題傾向があります。

任意科目から2科目を選択し，必須科目の2科目と合わせて合計4科目を解くことになります。上でもお伝えしたとおり，1次試験はスピード勝負で2次試験は思考力勝負になります。

必須科目の線形代数では，固有値・固有ベクトルの定義を押さえずにパターン化して暗記しているだけでは解けない問題や，表現行列の定義に関する問題が頻出です。必須科目の微分積分では，重積分を計算する問題や体積や立体を求積する問題が頻出です。微分方程式は必須科目の問7もしくは任意科目として出題されることもあります。

それでは，任意科目としてはどの問題を解くべきなのでしょうか。昔から言われていることは「任意科目は確率統計を選び，必ず1点を確保する。必須科目の線形代数と微分積分で1.5点を確保する。合計2.5点が取れれば合格できる。」というものですが，筆者もこの方針に賛成しています。2次試験において確率統計の問題はある程度パターン化されており，有名な区間推定と検定，及び線形回帰を押さえておけば，電卓が使用可能であることからまず満点が取れます。

問1の代数系の証明問題は非常に対策が難しく，ユークリッドの互助法やオイラーの定理をマスターするだけでは太刀打ちできない問題が出題されます。問2の解析系の証明問題 or 微分方程式はかなり狙い目ですが，連続性の議論など高度な内容を問われる場合があるため注意が必要です。問3の幾何問題は絶望的に難しく，数学オリンピックのような問題が出題されます。問5の独自問題の傾向は予測不能です。分野にとらわれない総合型の問題が出題されることが多く，例えば$n$進数を使えば簡単に解ける問題やコンパスを用いる作図問題も出題されます。

2次試験では関数電卓が使用可能なので，できる限り高性能な関数電卓を利用するようにしましょう。CASIOの関数電卓は昔から定番ですが，最近初学者にも扱いやすいClassWizシリーズが新発売されました。fx-JP{数字}CWという型番で，数字の部分には500,700,900が入って数字が大きいほど高性能になります。詳しくはCASIOの公式HPに記載がありますが，行列演算が可能な700もしくは900を選ぶとよいでしょう。

数学検定協会にCASIOのfx-JP700CWとfx-JP900CWが利用可能か問い合わせたところ，「具体的な機種に対する使用可否はお答えしかねます。通信機能または印刷機能がついていないものであれば関数電卓の使用が可能です。」という回答が返ってきました。機種ごとに使用可否を判断していては数学検定協会側の負荷が高いため回答できないということだと思います。いずれも通信機能や印刷機能はついていないので利用可能と判断できます。

おわりに

数検1級は1次試験が関門になり，2次試験は1次試験で出題され得る分野を広く押さえた上で確率統計の区間推定・検定・線形回帰を押さえられれば合格することができる試験だと思います。日本数学検定協会も明記していますが，1次試験は計算技能を見極める試験なので，持ち合わせている知識で解答を先回りする能力や数値を概算する能力，導出された結果が本当に正しいのか検算する能力などが問われることになります。

「1次試験は数学ではない。2次試験で問われる思考力こそが数学である。」という意見も散見されますが，1次試験で問われる能力も十分に数学の範疇だと思います。純粋数学なのかと問われると違うと思うのですが，実用検定という位置付けをしている以上，現実世界での応用を見据えないと検定が成り立たなくなってしまいます。1次試験はパターンで解くことができる問題は多いですが，そのパターンを適用するにも計算ミス等が頻発する世界ではあります。総合的な知識によって唯一の解答に自分の思考プロセスを収束させていく営みこそが，1次試験で問われる数学力であると筆者は考えています。知識で武装すればするほど解答への収束スピードが早まるので，1次試験の問題演習では複数の別解を考えてみたり，検算の方法を考えてみたりする対策が有効であると考えられます。

つらつらと書きましたが，数検1級は非常に楽しいものです。作問者の意図を汲み取って解答を導く面白さ，絶対に予想していなかったであろう解き方でねじ伏せる快感，武装した知識を活かすことができるゲーム感覚，色々な魅力が数学検定には詰まっています。ぜひ皆さんも楽しんで数学検定1級を取得しましょう。

Appendix

数検には様々な表彰制度があります。詳しくは公式HPに記載がありますが，個人賞としては

• 文部科学大臣賞（最優秀賞）
• グランプリ金賞（優秀賞）
• グランプリ会長賞（家族や年長者向け）
• 生涯学習功労賞（指導者向け）

といった賞が用意されています。文部科学大臣賞とグランプリ金賞の基準は公開されていませんが，1次試験と2次試験で満点を取ればいずれかの賞を受賞することができるのではないでしょうか。筆者もいつか取れるように継続的な学習を心掛けます。