本記事では,数学検定1級で頻出のトピックについてまとめていきます。
初学者の分かりやすさを優先するため,多少正確でない表現が混在することがあります。もし致命的な間違いがあればご指摘いただけると助かります。
定義
逆三角関数は名前の通り三角関数の逆関数です。単射でなければ,逆関数は存在しません。なぜなら,$y=f(x)$の関数$f$が単射でなければ,ある$y$の値に関して複数の$x$が対応してしまうからです。三角関数は,1つの$y$に対して複数の$x$が対応しますので,単射ではありません。このままでは逆関数を定義することはできません。
そこで,三角関数の定義域を絞ってあげることで,三角関数を単射にしてあげます。具体的には,以下のような定義域を考えます。
- $\sin x$:$-\pi / 2 \leq x \leq \pi / 2$
- $\cos x$:$0 \leq x \leq \pi$
- $\tan x$:$-\pi / 2 \leq x \leq \pi / 2$
こうすることで,それぞれの三角関数が単射になります。このとき,逆三角関数は以下のように定義されます。
- $\sin x\;(-\pi / 2 \leq x \leq \pi / 2)$の逆関数$\sin^{-1}x\;(-1 \leq x \leq 1)$を$\arcsin x$と書く
- $\cos x\;(0 \leq x \leq \pi)$の逆関数$\cos^{-1}x\;(-1 \leq x \leq 1)$を$\arccos x$と書く
- $\tan x\;(-\pi / 2 \leq x \leq \pi / 2)$の逆関数$\tan^{-1}x\;(-\infty \leq x \leq \infty)$を$\arctan x$と書く
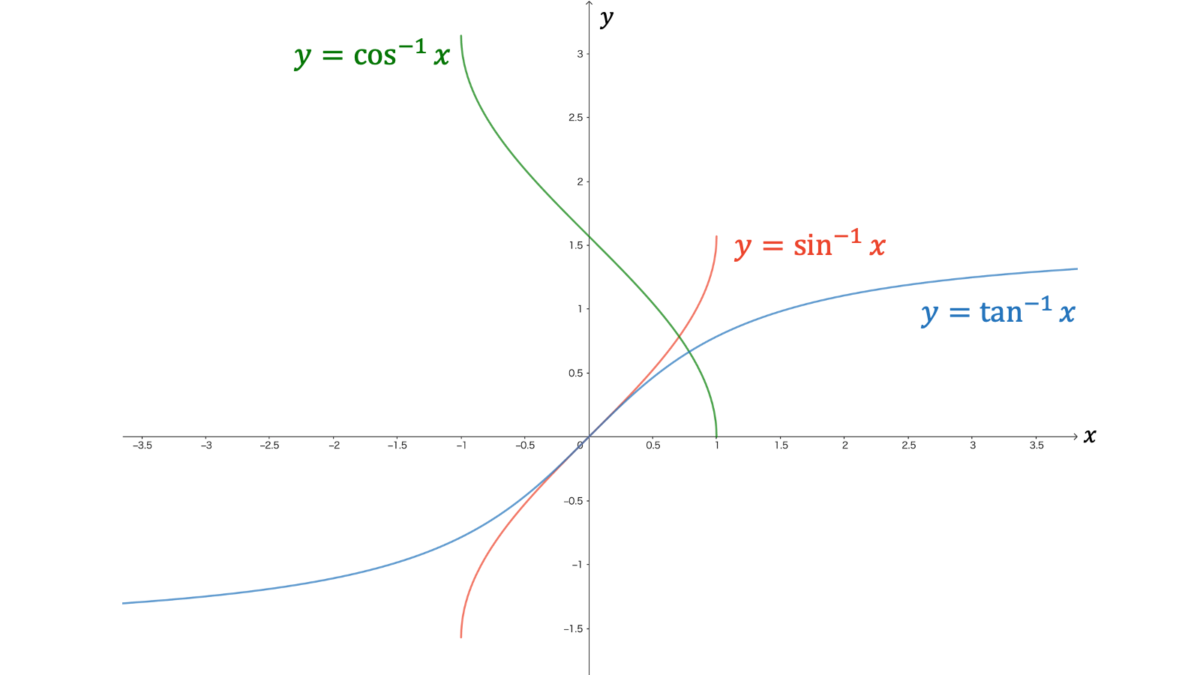
グラフ
逆関数のグラフは元の関数を$y=x$に関して折り返したようなグラフになります。
微分
\left( \arcsin x \right)^{\prime} &= \frac{1}{\sqrt{1 - x^2}} \\[0.7em]
\left( \arccos x \right)^{\prime} &= -\frac{1}{\sqrt{1 - x^2}} \\[0.7em]
\left( \arctan x \right)^{\prime} &= \frac{1}{1 + x^{2}}
\end{align}
逆三角関数の微分は覚える必要はありません。簡単に導出できるからです。ただし,定義域だけには注意する必要があります。先ほどお伝えしたように,三角関数を単射にするために定義域を絞りましたから,その値域(つまり逆関数の定義域)も絞られています。
さて,実際に逆三角関数の導関数を求めてみましょう。まずは,$\arcsin x$から求めていきます。$y = \sin^{-1}x$ですので,以下のように式変形することができます。
x &= \sin y \\[0.7em]
\frac{dx}{dy} &= \cos y \\[0.7em]
\end{align}
すると,$\cos y$は
\cos y &= \pm \sqrt{1 - \sin^2 y} \\[0.7em]
&= \pm \sqrt{1 - x^2}
\end{align}
となります。先ほどもお伝えした通り,逆三角関数の定義域は三角関数の値域に対応していますから,$-\pi / 2 \leq y \leq \pi / 2$となります。したがって,$\cos y$の候補のうち正の値が採用されて
\cos y &= \sqrt{1 - x^2}
\end{align}
となりますので,$dy/dx$は以下のように求められます。
\frac{dy}{dx} &= \frac{1}{\cos y} \\
&= \frac{1}{\sqrt{1 - x^2}}
\end{align}
$\arccos x$と$\arctan x$も同様にして求められます。
積分
\int \arcsin x dx &= x\arcsin x + \sqrt{1 - x^2} + C \\[0.7em]
\int \arccos x dx &= x\arccos x - \sqrt{1 - x^2} + C \\[0.7em]
\int \arctan x dx &= x\arctan x - \frac{\ln(x^2 + 1)}{2} + C
\end{align}
逆三角関数自体の積分は部分積分法を利用します。$\arcsin x$を例にとって計算してみましょう。
\int \arcsin x dx &= \int (x)^{\prime} \arcsin x dx \\[0.7em]
&= x \arcsin x - \int x (\arcsin x)^{\prime} dx \\[0.7em]
&= x \arcsin x - \int \frac{x}{\sqrt{1-x^2}} dx \\[0.7em]
&= x \arcsin x + \sqrt{1-x^2} + C
\end{align}
$\arccos x$と$\arctan x$に関しても同様の計算で求めることができます。他にも,逆三角関数にまつわる積分もあります。「微分するとこの形になる関数は逆三角関数だよね」という発想です。
\int \frac{1}{\sqrt{a^2 - x^2}} dx &= \arcsin \frac{x}{a} + C \\[0.7em]
\int \frac{1}{a^2 + x^2} dx &= \frac{1}{a}\arctan \frac{x}{a} + C
\end{align}
これらは,先ほど示した逆三角関数の導関数の結果を用いて示すことができます。定数項$a$が付いていますが,本質的な操作は変わりません。


コメント