本記事は「これなら分かる!はじめての数理統計学」シリーズに含まれます。
不適切な内容があれば,記事下のコメント欄またはお問い合わせフォームよりご連絡下さい。
正規分布
f_{X}(x) &= \frac{1}{\sqrt{2\pi\sigma^2}}\exp\left\{ -\frac{1}{2\sigma^2} (x-\mu)^2 \right\} \\[0.7em]
M_{X}(t) &= \exp \left( \mu t + \frac{1}{2}\sigma^2t^2 \right) \\[0.7em]
E[X] &= \mu \\[0.7em]
V[X] &= \sigma^2
\end{align}
二項分布$\Bin (n, p)$において,$p$を一定に保ったまま$n$と$x$を大きくしていくと,正規分布
\N (\mu, \sigma^2)
\end{align}
が得られます。正規分布に従う確率変数$X$に対し,実現値は
x \in \bbR
\end{align}
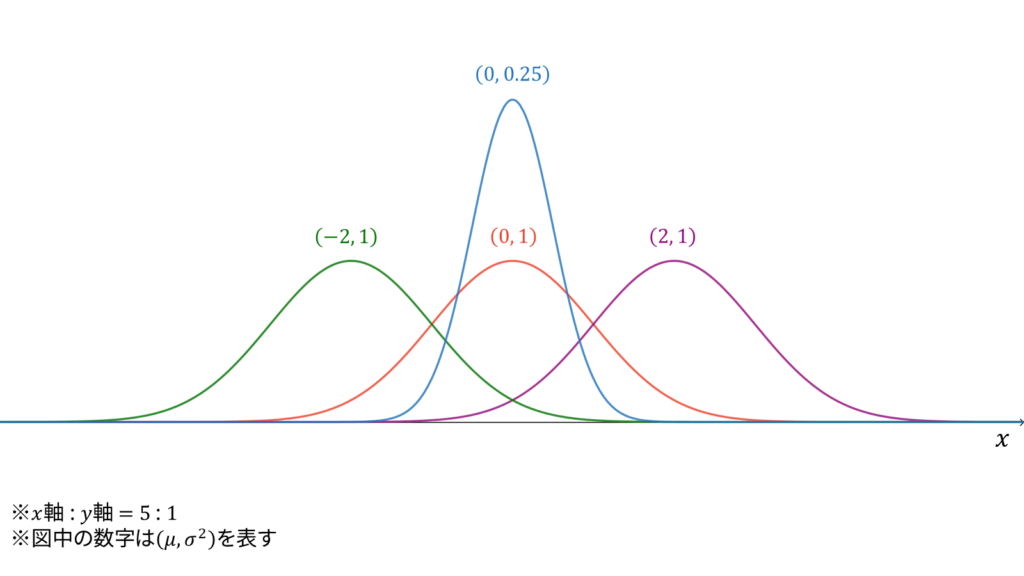
であり,モーメント母関数の変数は$t \in \bbR$とします。正規分布は再生性を持ち,ロードマップ中では二項分布とポアソン分布の極限に相当します。同時に,正規分布は「正規系」の源流となる分布です。直感的には,二項分布の連続拡張が正規分布です。
確率密度関数
椎名 [1] によると,正規分布には七つの導出方法があります。これらの中でも,大学の講義などでよく採用される方法は以下の二つです。
- 二項分布の極限としての証明
- 誤差の公理に基づくガウスの証明
二項分布の極限としての証明では,ある程度数学的な厳密性を担保しながら正規分布の確率密度変数を導出できます。一方で,誤差の公理に基づくガウスの証明では,正規分布の意味を解釈するという意味で非常に効果的です。そこで,歴史上数多く提案されてきた正規分布の導出方法のうち,本節では特によく扱われる上記二つの方法に着目して解説を行っていきます。
二項分布の極限としての証明
本パートでは,二項分布の極限として正規分布の確率密度関数を導出していきます。流れは以下の通りです。
- 二項分布の確率質量関数の対数を取り$g(x)$とおく
- $g(x)$を$\mu$のまわりにテーラー展開する
- 第三項目以降は無視する
- スターリングの近似を用いる
- 定数項を求める
まず,二項分布の対数を取ります。これは,確率質量関数は対数領域で計算した方が簡単になることが多いからです。テーラー展開が出てくるのは,離散分布である二項分布を連続分布に拡張するために,多項式近似を行って極限を取る(今回はスターリングの近似で代用する)という方針を採用するからです。$\mu$の周りでテーラー展開するのは,$x$が$\mu$の近くにたくさん存在するという気持ちを近似に反映させたいからです。
「なぜ第三項目以降目を無視するのか」という疑問に対しては「そうすると綺麗に導出できるから」としか答えられません。逆に言えば,$\mu$のまわりのテーラー展開において,第三項目以降を無視した場合に正規分布は導出されるとも捉えられます。スターリングの近似が出てくるのは,$n$が十分大きい状態であることを前提とすることで連続性を表すと同時に,二項分布の確率質量関数に出現する階乗の形を簡単にするためです。最後に,正規分布が確率密度関数の定義を満たすように定数倍を調整すれば証明完了です。
正規分布発見の歴史については,文献 [2] が詳しいです。二項分布の極限として正規分布を発見したのは,ド・モアブルと言われています。この発見をもとに,ラプラス変換でも知られているラプラスは,離散変数に対する中心極限定理の厳密な証明を与えました。その後,チェビシェフやマルコフらが中心極限定理の一般的な場合への拡張を試み,連続変数に対する中心極限定理の厳密な証明はLindebergとLevyらによって与えられたとされています。実際,中心極限定理を満たす母集団の性質を記述する定理はLindeberg条件と呼ばれています。正規分布の別名はガウス分布ですが,これはガウスが天文学的な観点から正規分布を導出したことに由来しています。後述しますが,ガウスは誤差の公理と微分方程式を利用して正規分布を導出しました。
早速,二項分布の極限としての正規分布を導出していきたいと思います。まずは,二項分布の確率質量関数の対数を取ったものを$g(x)$とおきます。
g(x) &= \log {}_n C_{x} p^x q^{n-x} \\[0.7em]
&= \log \left\{ \frac{n!}{x! (n-x)!} p^x q^{n-x} \right\} \\[0.7em]
&= \log n!-\log x!-\log (n-x)! + x\log p + (n-x)\log q
\end{align}
続いて,$g(x)$を$\mu$のまわりにテーラー展開して第3項以降を無視します。
g(x) &= g(\mu) + \frac{g'(\mu)}{1!} (x-\mu) + \frac{g^{''}(\mu)}{2!} (x-\mu)^2 + \cdots \\[0.7em]
&\simeq g(\mu) + \frac{g'(\mu)}{1!} (x-\mu) + \frac{g^{''}(\mu)}{2!} (x-\mu)^2
\end{align}
以下では,$g^{\prime}(\mu)$と$g^{\prime\prime}(\mu)$を求めたいと思います。計算を簡単にするため,$g(x)$をシンプルな形で書き換えておきましょう。今回は,スターリングの公式を利用して,階乗を除去しておきます。
十分大きい$n$に対し,
\log n! \simeq n\log n-n
\end{align}
が成り立つ。
最終的にはサンプル数$n$が多い場合を考えますので,スターリングの公式が成り立つものとしてOKです。
g(x) &= \log n!-\log x!-\log (n-x)! + x\log p + (n-x)\log q \\[0.7em]
&\simeq (n\log n-n)-(x\log x-x) \notag \\[0.7em]
&\quad-\left\{ (n-x)\log(n-x)-(n-x) \right\} + x\log p + (n-x)\log q \\[0.7em]
&= n\log n-x\log x-(n-x)\log (n-x) + x\log p + (n-x) \log q
\end{align}
さて,$g^{\prime}(x)$と$g^{\prime\prime}(x)$を求めていきましょう。
g'(x) &= -(\log x+1)-\left\{ -\log(n-x)-1 \right\} + \log p-\log q \\[0.7em]
&= \log (n-x)-\log x + \log p-\log q \\[0.7em]
&= \log \frac{p(n-x)}{qx} \\[0.7em]
g^{''}(x) &= -\frac{1}{n-x}-\frac{1}{x} \\[0.7em]
&= -\frac{n}{x(n-x)}
\end{align}
したがって,$g'(\mu)$と$g^{''}(\mu)$は以下のようになります。
g'(\mu) &= \log \frac{p(n-\mu)}{q\mu} \\[0.7em]
&= \log \frac{p(n-np)}{npq} \\[0.7em]
&= \log \frac{npq}{npq} \\[0.7em]
&= 0\\[0.7em]
g^{''}(x) &= -\frac{n}{\mu (n-\mu)} \\[0.7em]
&= -\frac{n}{np(n-np)} \\[0.7em]
&= -\frac{1}{npq} \\[0.7em]
&= -\frac{1}{\sigma^2}
\end{align}
ただし,二項分布の分散が$npq$となることを利用しました。したがって,テーラー展開による二項分布の近似式は以下のようになります。
g(x) &= g(\mu)-\frac{1}{2\sigma^2} (x-\mu)^2
\end{align}
ここで,$g(\mu)$は定数ですので,$C=g(\mu)$と置いてしまいましょう。
g(x) &= \log e^{C} + \log \exp \left\{ -\frac{1}{2\sigma^2} (x-\mu)^2 \right\} \\[0.7em]
&= \log \left[ e^{C} \cdot \exp \left\{ -\frac{1}{2\sigma^2} (x-\mu)^2 \right\} \right]
\end{align}
正規分布の確率密度関数を$f(x)$とおくと,
g(x) &= \log f(x) \\[0.7em]
&= \log \left[ c \cdot \exp \left\{ -\frac{1}{2\sigma^2} (x-\mu)^2 \right\} \right]
\end{align}
となります。ただし,$c=e^{C}$と置きました。したがって,正規分布の確率密度関数は以下のように表されます。
f(x) &= c \cdot \exp \left\{ -\frac{1}{2\sigma^2} (x-\mu)^2 \right\}
\end{align}
後は,$c$を求めれば正規分布の確率密度関数を完全に求めることができます。一般に,確率密度関数は積分して$1$になりますので,定数$c$は
\int_{-\infty}^{\infty} c \cdot \exp \left\{ -\frac{1}{2\sigma^2}(x-\mu)^2\right\} dx &= 1 \label{eq_def_pdf}
\end{align}
を満たすように定めます。$e^{-x^2}$の形が出現しているため,以下のガウス積分に持ち込むことを考えます。
\int_{-\infty}^{\infty} e^{-x^{2}} d x=\sqrt{\pi}
\end{align}
ガウス積分の形に近づけるため,指数部分をまとめて$u$とおいてしまいましょう。
u &= \frac{x-\mu}{\sqrt{2 \sigma^2}} \\[0.7em]
dx &= \sqrt{2 \sigma^2} du
\end{align}
結局,式($\ref{eq_def_pdf}$)は以下のように表されます。
\int_{-\infty}^{\infty} c \cdot e^{-u^2} \sqrt{2 \sigma^2} du
&= \sqrt{2 \sigma^2} c \int_{-\infty}^{\infty} e^{-u^2} du \\[0.7em]
&= \sqrt{2 \sigma^2} c \cdot \sqrt{\pi} \\[0.7em]
&= 1
\end{align}
したがって,定数部分が求められました。
c &= \frac{1}{\sqrt{2\pi \sigma^2}}
\end{align}
以上をまとめると,正規分布の確率密度関数は
f(x) &= \frac{1}{\sqrt{2\pi \sigma^2}} \exp \left\{ -\frac{1}{2\sigma^2}(x-\mu)^2\right\}
\end{align}
となり,導出が完了しました。
ガウスによる証明
天文学者であったガウスは,測定誤差に関する研究を行っていました。1809年当時,天文学の分野では装置や人間に起因する誤差が発生することが多く,測定誤差を数学的に扱いたいというモチベーションが存在していたのです。経験的には,できるだけ多くの測定値を手に入れて,それらの平均を取ることで誤差が「均される」という共通認識はあったものの [3] ,まだ理論的な裏付けがないような状況でした。
このような背景の下,ガウスは星の軌道計算を非線形関数に当てはめる趣旨の論文 [3-5] を発表しました。本論文の中で,正規分布の確率密度関数が導かれています。具体的には,以下の仮定を置きます。
- 標本平均は真の値の最尤推定値となる
- 誤差の分布は対称形となる
※本稿では,これらを「ガウスの仮定」と表すことにします。
文献 [5] よりガウスの言葉を借用すると,1.は「全ての観測値の相加平均は,絶対的な厳密さでないまでも,少なくとも最確値に非常に近い値を与えることは,普通は公理として扱われる仮説である。すなわち,この方法を採用することはいつももっとも安全であるとみなされる。」と表現されています。当時は最尤推定法が理論として確立されている訳ではありませんでしたので,このような婉曲表現になっています。また,2.は「おのおのの観測に際し,同じ大きさの誤差は同程度に確からしいとみなす」と表現されています。
なお,多くの書籍では以下をガウスの公理と表しています。
- 小さな誤差は大きな誤差より起こりやすい
- 大きさの等しい正と負の誤差は等しい確率で生じる
- ある限界値より大きな誤差はほとんど起こらない
文献 [5] よりガウスの言葉を借用すると,1.は「誤差が大きくなれば確率は小さくなるという法則」と表現されています。円錐曲線で太陽のまわりを回る天体の運動理論に関する論文 [4] で正規分布の確率密度関数が導出された背景も,「この法則と確からしい軌道との関連について,我々は今後よい大きな一般性のもとでこの研究に取組むつもりであり,それは決して利益のない投機とみなすべきではないだろう」と表現されています。2.は先ほどと同様に「おのおのの観測に際し,同じ大きさの誤差は同程度に確からしいとみなす」と表現されています。3.は「最大の誤差をとるかまたはそれより大きい値をとるときは$0$になることは保証される」と表現されています。ただし,ガウスは3.に関して,本来は誤差の分布としては離散型確率分布を考えるべきだとしていますが,連続分布で3.を表現するためには無限大の誤差を考えたときに漸近的に$0$に収束するべきだとしています。
加えて,多くの書籍では以下をガウスによる仮定と表しています。
- 標本平均は真の値の最尤推定値となる
つまり,本稿では一般的なガウスの公理のうち「大きさの等しい正と負の誤差は等しい確率で生じる」を「誤差の分布は対称形となる」として用いることに加え,「標本平均は真の値の最尤推定値となる」という仮定に基づくことで,正規分布の確率密度関数を導出していきます。
上述の一般的なガウスの公理に基づくことでも正規分布の確率密度は導出されますが,本稿では二つの仮定のみを考える最もシンプルな方法を採用します。なお,「小さな誤差は大きな誤差よりも起こりやすい」は「標本平均は真の値の最尤推定値となる」で代用可能であり,「ある限界値より大きな誤差はほとんど起こらない」は「確率密度関数の積分が$1$になる」という定義で代用可能です。
いま,真の重さが$\mu$であるゴルフボールを製造している工場で,製品の重さを$n$回計測する試行を考えましょう。各試行で得られる標本値(実現値)を$x_i$,誤差を$\varepsilon_i$,誤差が従う確率密度関数を$f$と置きます。我々の目的は,誤差の従う分布$f$を求めることです。
まず,定義を確認しましょう。誤差は標本値と真の値の差として定義されます。
\varepsilon_i &= x_i-\mu \label{eq:epsilon}
\end{align}
誤差は正にも負にもなります。式($\ref{eq:epsilon}$)の定義に従えば,標本値の方が大きければ正に,真の値の方が大きければ負になります。
今回は,$n$サンプルの製品を独立に抽出することを考えますので,同時確率密度関数$g$は以下のように各試行の積で表されます。
g(\varepsilon_1,\ldots, \varepsilon_n) &= \prod_{i=1}^{n} f(\varepsilon_i)
\end{align}
ここで,ガウスは最尤推定の考え方を利用します。すなわち,得られた観測値$x_1, \ldots, x_n$を定数として,母数$\mu$をパラメータとして推定するという考え方です。ガウスの公理の一つ目に基づけば,母数$\mu$の最尤推定値は標本平均になります。言い換えると,$g$を$\mu$の関数と捉えたときに,$g$を最大にする$\mu$は標本平均になるということです。そこで,まずは誤差の定義($\ref{eq:epsilon}$)を用いて,$g$を$\mu$の関数として捉えましょう。
g(\mu) &=\prod_{i=1}^{n} f(x_i-\mu)
\end{align}
さらにガウスの公理の一つ目を言い換えると,標本平均は$g$の導関数を$0$にする必要があるということになります。したがって,標本平均を
\ox &= \frac{1}{n} \sum_{i=1}^{n} x_i
\end{align}
とおくと,ガウスの公理の一つ目は以下のように表されます。
\left. \frac{\partial}{\partial \mu} g(\mu) \right|_{\mu=\ox} &= 0 \label{g_prime_0}
\end{align}
導関数が$0$であってもその点が最大値を取る保証はありませんので,式($\ref{g_prime_0}$)はあくまでも必要条件になります。しかし,必要性や十分性の精密な議論は趣旨と逸れるため,本稿では行いません。
$g$の導関数は以下のように計算されます。
\frac{\partial g}{\partial \mu} &=-\left\{ f^{\prime}(x_1-\mu)f(x_2-\mu)\cdots f(x_n-\mu) \right\}\ldots-\left\{ f(x_1-\mu)\cdots f^{\prime}(x_n-\mu) \right\} \\[0.7em]
&=-g(\mu)\cdot \left\{ \frac{f^{\prime}(x_1-\mu)}{f(x_1-\mu)}\ldots+ \frac{f^{\prime}(x_n-\mu)}{f(x_n-\mu)} \right\} \\[0.7em]
&=-g(\mu) \sum_{i=1}^{n} h(x_i-\mu)
\end{align}
ただし,$i=1,\ldots,n$に対して,
h(x_i-\mu) &= \frac{f^{\prime}(x_i-\mu)}{f(x_i-\mu)}
\end{align}
と置きました。したがって,式($\ref{g_prime_0}$)は以下のように変形できます。
\left. \frac{\partial}{\partial \mu} g(\mu) \right|_{\mu=\ox} &=-g(\ox) \sum_{i=1}^{n} h(x_i-\ox) \\[0.7em]
&= 0 \label{eq:g=0}
\end{align}
ここで,変数を$\mu$から$x_i$にシフトします。同時確率密度関数$g(\ox)$が$0$となるのは,全ての測定値$x_i$が真の値$\mu$と等しいときですが,そのようなケースは今回は範疇外とします。よって,$g(\ox)\neq 0$とすることができます。すると,式($\ref{eq:g=0}$)より
\sum_{i=1}^{n} h(x_i-\ox) &= 0 \label{eq:ff}
\end{align}
が導かれます。ここで,やや天下りなのですが,任意の確率変数$Y$とその実現値$y$に対し,測定結果$x_1,\ldots,x_n$が以下を満たすとします。
x_1 &= \mu \label{eq:x_1}\\[0.7em]
x_2 &= \mu-ny \label{eq:x_2} \\[0.7em]
&\vdots \notag \\[0.7em]
x_n &= \mu-ny \label{eq:x_n}
\end{align}
一番の引っかかりポイントだと思います。$f$が誤差の確率分布である限り,観測値が式($\ref{eq:x_1}$)-($\ref{eq:x_n}$)のような状況も許容しなくてはならないことを利用します。これらの十分条件が唐突に思われるかもしれませんが,後に微分方程式を解きやすい形で手に入れるための伏線であると理解しておきましょう。なお,上でもお伝えした通り,本稿では必要性や十分性の精密な議論は行いません。
観測値が式($\ref{eq:x_1}$)-($\ref{eq:x_n}$)を満たすとき,標本平均は以下のように表されます。
\ox &= \frac{1}{n} \sum_{i=1}^{n} x_i \\[0.7em]
&= \frac{1}{n} \left\{ \mu + \sum_{i=2}^{n}\left(\mu-ny\right) \right\} \\[0.7em]
&= \frac{1}{n} \left\{ \mu + (n-1)\mu-n(n-1)y \right\} \\[0.7em]
&= \mu-(n-1)y
\end{align}
これらを式($\ref{eq:ff}$)に代入すると,以下が得られます。
&h(x_1-\ox) + \sum_{i=2}^{n} h(x_i-\ox) \notag \\[0.7em]
&= h\left(\mu-\mu+(n-1)y\right) + \sum_{i=2}^{n} h\left(\mu-ny-\mu+(n-1)y\right) \\[0.7em]
&= h\left((n-1)y\right) + \sum_{i=2}^{n} h(-y) \\[0.7em]
&= h\left((n-1)y\right) + (n-1)h(-y) \\[0.7em]
&= 0
\end{align}
すなわち,以下が得られます。
h\left((n-1)y\right) &=-(n-1)h(-y) \label{eq:caucy_before}
\end{align}
ここで,ガウスの公理の$2$つ目に注目しましょう。誤差の分布が左右対称であることから,以下が成り立ちます。
f(-x) &= f(x) \\[0.7em]
f^{\prime}(-x) &=-f^{\prime}(x)
\end{align}
したがって,$h(x)$は以下のように奇関数であることが分かります。
h(-x) &= \frac{f^{\prime}(-x)}{f(-x)} \\[0.7em]
&=-\frac{f^{\prime}(x)}{f(x)} \\[0.7em]
&=-h(x) \label{eq:h_odd}
\end{align}
式($\ref{eq:h_odd}$)を式($\ref{eq:caucy_before}$)に代入しましょう。
h\left((n-1)y\right) &=(n-1)h(y) \label{eq:caucy_after}
\end{align}
ここで,式($\ref{eq:caucy_after}$)が定数倍に関する関数方程式の形をしていることに注目します。
$\alpha\in \bbR$としたとき,定数倍に関する以下の関数方程式
f(\alpha x) &= \alpha f(x)
\end{align}
を満たす連続関数$f$は$f(x)=ax$のみである。ただし,$a\in \bbR$とする。
式($\ref{eq:x_1}$)-($\ref{eq:x_n}$)は,ここで定数倍に関する関数方程式を手に入れるための十分条件だったのです。
したがって,式($\ref{eq:caucy_after}$)を満たす連続関数$h$も$h(x)=ax$のみになります。$h(x)$の定義に注意すると,以下の微分方程式が得られます。
\frac{f^{\prime}(x)}{f(x)} &= ax
\end{align}
左辺が対数関数の微分形であることに注意すれば,
\log f(x) &= \frac{1}{2}ax^2 + C
\end{align}
と解くことができます。すなわち,以下が得られます。
f(x) &= c \cdot \exp\left(\frac{1}{2}ax^2\right)
\end{align}
ただし,$e^C=c$とおきました。ここで,$f$が確率密度関数であることに注意すると,$a$は負でなければなりません。なぜなら,$a$が正であると仮定すると,以下の積分
\int_{-\infty}^{\infty} f(x) dx &= \int_{-\infty}^{\infty} c \cdot \exp\left(\frac{1}{2}ax^2\right) dx
\end{align}
が発散してしまい,確率密度関数の定義を満たさなくなってしまうからです。そこで,$a=-a$と新たに置き換えることにし,$a>0$とします。
f(x) &= c \exp\left(-\frac{1}{2}ax^2\right)
\end{align}
改めて,$f$は確率密度関数の定義を満たしますので,
\int_{-\infty}^{\infty} c \exp\left(-\frac{1}{2}ax^2\right) dx &= 1
\end{align}
が成り立ちます。積分はガウス分布の形をしています。
\int_{-\infty}^{\infty} e^{-ax^2/2} d x=\sqrt{\frac{2\pi}{a}}
\end{align}
したがって,以下が成り立ちます。
c &= \sqrt{\frac{a}{2\pi}} \label{正規分布:連立1}
\end{align}
ここで,$\sigma^2$が分散を表していることに注意すると,分散の定義と部分積分を用いて以下のように式変形できます。
\sigma^2 &= \int_{-\infty}^{\infty} x^{2} f(x) dx \\[0.7em]
&=\int_{-\infty}^{\infty} x^{2} c \cdot \exp \left(-\frac{a}{2} x^{2}\right) dx \\[0.7em]
&=c\int_{-\infty}^{\infty} x^2 \left\{-\frac{1}{ax} \exp \left(-\frac{a}{2} x^{2}\right) \right\}^{\prime} dx \\[0.7em]
&=-\frac{c}{a}\left\{\left[x\exp \left(-\frac{a}{2} x^{2}\right)\right]_{-\infty}^{\infty}-\int_{-\infty}^{\infty} \exp \left(-\frac{a}{2} x^{2}\right) dx \right\}
\end{align}
第一項目は$0$となりますが,第二項目で先ほどのガウス積分を利用します。
\frac{c}{a}\int_{-\infty}^{\infty} \exp \left(-\frac{a}{2} x^{2}\right) dx
&=\frac{c}{a} \sqrt{\frac{2 \pi}{a}} \\[0.7em]
&= \sqrt{\frac{a}{2\pi}} \cdot \frac{1}{a} \cdot \sqrt{\frac{2\pi}{a}} \\[0.7em]
&= \frac{1}{a}
\end{align}
したがって,$a$は分散の逆数であることが分かりました。
a &= \frac{1}{\sigma^2}
\end{align}
以上から,$f$の形が得られました。
f(x) &= c \cdot \exp\left(\frac{1}{2}ax^2\right) \\[0.7em]
&= \frac{1}{\sqrt{2\pi \sigma^2}} \exp\left(-\frac{x^2}{2 \sigma^2}\right)
\end{align}
全体を$\mu$だけ平行移動させた関数を改めて$f(x)$とおけば,正規分布の確率密度関数が得られます。
f(x) &= f(x-\mu) \\[0.7em]
&=\frac{1}{\sqrt{2\pi \sigma^2}} \exp\left\{-\frac{(x-\mu)^2}{2 \sigma^2}\right\}
\end{align}
これだけシンプルに定式化できることからも分かる通り,多くの研究では慣習として誤差に正規分布を仮定します。一方で,どんな状況でも誤差に正規分布を仮定できる訳ではなく,代替手段としてチェビシェフの不等式やCamp-Meidellの不等式が用いられます [6]。ただし,正規分布を仮定しない手法は正規分布を仮定する手法と比べて不便で,確定的な情報が得にくくなります [7-9]。
モーメント母関数
モーメント母関数の定義に従って計算していきます。
M_{X}(t) &= E[e^{tX}] \\[0.7em]
&= \int_{-\infty}^{\infty} \frac{1}{\sqrt{2\pi \sigma^2}} \exp\left\{-\frac{(x-\mu)^2}{2 \sigma^2} + tx\right\} dx \\[0.7em]
&= \frac{1}{\sqrt{2\pi \sigma^2}} \int_{-\infty}^{\infty}\exp\left\{-\frac{1}{2\sigma^2}\left( x^2 + -2\mu x + 2\sigma^2tx + \mu^2 \right) \right\} dx \\[0.7em]
&= \frac{1}{\sqrt{2\pi \sigma^2}} \int_{-\infty}^{\infty}\exp\left[-\frac{1}{2\sigma^2}\left\{ x-(\mu + \sigma^2t)\right\}^2 + \mu t + \frac{\sigma^2 t^2}{2} \right] dx \\[0.7em]
&= \exp\left(\mu t + \frac{\sigma^2 t^2}{2} \right)\frac{1}{\sqrt{2\pi \sigma^2}} \int_{-\infty}^{\infty}\exp\left[-\frac{1}{2\sigma^2}\left\{ x-(\mu + \sigma^2t)\right\}^2 \right] dx \\[0.7em]
&= \exp\left(\mu t + \frac{\sigma^2 t^2}{2} \right)
\end{align}
ただし,最終行では正規分布の確率密度関数の積分が$1$となることを利用しました。
平均・分散
連続分布の平均と分散を求めるためには,モーメント母関数の性質を利用します。まず,一次モーメント,すなわち期待値を求めます。
E[X] &= \left. \frac{d M_{X}(t)}{d t} \right|_{t=0} \\[0.7em]
&= \left. \left( \mu + \sigma^2 t \right) \exp\left(\mu t + \frac{\sigma^2 t^2}{2} \right) \right|_{t=0}\\[0.7em]
&= \mu
\end{align}
続いて,二次モーメントを求めます。
E[X^2] &= \left. \frac{d^2 M_{X}(t)}{d t^2} \right|_{t=0} \\[0.7em]
&= \left. \sigma^2\exp\left(\mu t + \frac{\sigma^2 t^2}{2} \right) \right|_{t=0} + \left. \left( \mu + \sigma^2 t \right)^2 \exp\left(\mu t + \frac{\sigma^2 t^2}{2} \right) \right|_{t=0}\\[0.7em]
&= \sigma^2 + \mu^2
\end{align}
最後に,一次モーメントと二次モーメントから分散を求めます。
V[X] &= E[X^2]-E[X]^2\\[0.7em]
&= \sigma^2 + \mu^2-\mu^2 \\[0.7em]
&= \sigma^2
\end{align}
正規分布の導出を逆に追っているイメージです。ガウスによる証明では,分散が$\sigma^2$となるように定数項を定めましたよね。
再生性
再生性を示すためには,再生性を示したい分布に従う独立な二つの確率変数を考え,その和のモーメント母関数を計算したときに,パラメータが和の形になっていることを示します。いま,二つの独立な確率変数
X &\sim \N(\mu_x, \sigma^2_x) \\[0.7em]
Y &\sim \N(\mu_y, \sigma^2_y)
\end{align}
を考えます。このとき,$X+Y$のモーメント母関数を計算します。
M_{X+Y}(t) &= M_{X}(t) \cdot M_{Y}(t) \\[0.7em]
&= \exp\left(\mu_x t + \frac{\sigma^2_x t^2}{2} \right) \cdot \exp\left(\mu_y t + \frac{\sigma^2_y t^2}{2} \right)\\[0.7em]
&= \exp\left\{\left(\mu_x + \mu_y \right) t + \frac{\left(\sigma^2_x + \sigma^2_y \right) t^2}{2} \right\}
\end{align}
これは,$X+Y$のモーメント母関数が正規分布のモーメント母関数であることを示しています。つまり,
X+Y &\sim \calN(\mu_x + \mu_y, \sigma^2_x + \sigma^2_y)
\end{align}
であり,正規分布の再生性を示しています。
ロードマップ
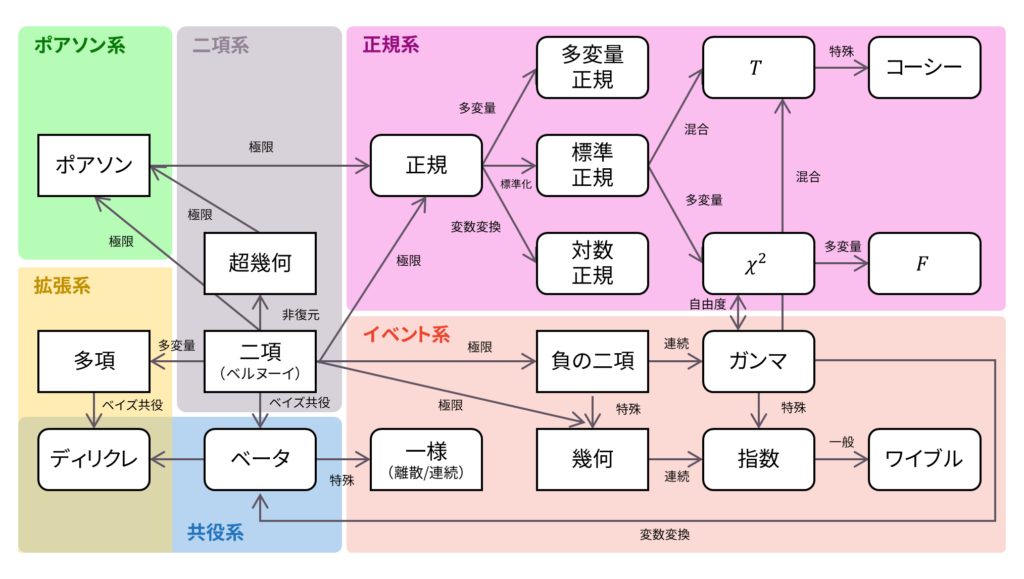
さて,ロードマップに戻りましょう。 正規分布は二項分布の極限として導出できました。ガウスの仮定に基づけば,誤差の分布が正規分布で表されることも分かりました。本稿の「正規系」は,この正規分布を出発点としますのでよくおさえておいて下さい。以下の内容も参考になるでしょう。
参考文献
本稿の執筆にあたり参考にした文献は,以下でリストアップしております。
なお,本記事における文献番号は以下です。
[1] 椎名乾平: "七つの正規分布." 日本心理学会, 2011.
[2] H. Fischer: "A History of the Central Limit Theorem: from Classical to Modern Probability Theory." Springer, 2010.
[3] C. F. Gauss: "Theoria motus corporum coelestium in sectionibus conicis solem ambientium." 1809.
[4] Translated by C.H. Davis : "Theory of the motion of the heavenly bodies moving about the Sun in conic sections." Little Brown, 1963.
[5] C. F. Gauss (原著), 飛田武幸, 石川耕春 (訳): "誤差論." 紀伊國屋書店, 1981.
[6] 兵藤申一: "物理学実験者のための13章." 東京大学出版会, 1989.
[7] ウィリアム・フェラー: "確率論とその応用 I." 紀伊國屋書店, 1960.
[8] 河田 竜夫, 国沢 清典: "現代統計学." 広川書店, 1956.
[9] R.A. フィッシャー (原著), 遠藤 健児, 鍋谷 清治 (訳): "研究者のための統計的方法 POD版." 森北出版, 2013.


コメント