本記事は「これなら分かる！はじめての数理統計学」シリーズに含まれます。
不適切な内容があれば，記事下のコメント欄またはお問い合わせフォームよりご連絡下さい。
目次
幾何分布
\begin{align}
f_{X}(x) &= p(1-p)^x \\[0.7em]
G_{X}(s) &= \frac{p}{1-(1-p)s} \\[0.7em]
E[X] &= \frac{1-p}{p}\\[0.7em]
V[X] &= \frac{1-p}{p^2}
\end{align}
f_{X}(x) &= p(1-p)^x \\[0.7em]
G_{X}(s) &= \frac{p}{1-(1-p)s} \\[0.7em]
E[X] &= \frac{1-p}{p}\\[0.7em]
V[X] &= \frac{1-p}{p^2}
\end{align}
無限に続くベルヌーイ試行において，成功するまでの失敗の回数$X$は幾何分布に従います。幾何分布に従う確率変数$X$に対し，実現値は
\begin{align}
x\in\{0, \ldots, n\}
\end{align}
x\in\{0, \ldots, n\}
\end{align}
であり，確率母関数の変数は$|s|\leq 1$とします。幾何分布は再生性を持たず，ロードマップ中では負の二項分布の特殊な場合に相当します。
確率密度関数
幾何分布はコイントスで「初めて表が出るまでの失敗の回数」を確率変数とする分布です。この定義から，以下の確率密度関数は自然に導かれます。
\begin{align}
f_{X}(x) &= p(1-p)^x\quad
\end{align}
f_{X}(x) &= p(1-p)^x\quad
\end{align}
確率母関数
確率母関数の定義に従って計算していきます。等比級数の公式を利用します。
\begin{align}
G_{X}(s) &= E[s^x]\\[0.7em]
&= \sum_{x=0}^{\infty} s^x\cdot p(1-p)^x\\[0.7em]
&= p\cdot \frac{1}{1-s(1-p)}\\[0.7em]
&= \frac{p}{1-(1-p)s}
\end{align}
G_{X}(s) &= E[s^x]\\[0.7em]
&= \sum_{x=0}^{\infty} s^x\cdot p(1-p)^x\\[0.7em]
&= p\cdot \frac{1}{1-s(1-p)}\\[0.7em]
&= \frac{p}{1-(1-p)s}
\end{align}
平均・分散
離散分布の平均と分散を求めるためには，確率母関数の性質を利用します。
\begin{align}
E[X] &= \left.\frac{d G_{X}(s)}{d s}\right|_{s=1}\\[0.7em]
&= \left. \frac{p(1-p)}{\left\{1-(1-p)s\right\}^2 } \right|_{s=1}\\[0.7em]
&= \frac{1-p}{p}\\[0.7em]
E[X(X-1)] &= \left.\frac{d^2 G_{X}(s)}{d s^2}\right|_{s=1}\\[0.7em]
&= \left. \frac{2p(1-p)^2}{\left\{1-(1-p)s\right\}^3 } \right|_{s=1}\\[0.7em]
&= \frac{2(1-p)^2}{p^2}\\[0.7em]
V[X] &= E[X^2] - E[X]^2\\[0.7em]
&= E[X(X-1)] + E[X] - E[X]^2\\[0.7em]
&= \frac{2(1-p)^2}{p^2} + \frac{1-p}{p} - \frac{(1-p)^2}{p^2}\\[0.7em]
&= \frac{1-p}{p^2}
\end{align}
E[X] &= \left.\frac{d G_{X}(s)}{d s}\right|_{s=1}\\[0.7em]
&= \left. \frac{p(1-p)}{\left\{1-(1-p)s\right\}^2 } \right|_{s=1}\\[0.7em]
&= \frac{1-p}{p}\\[0.7em]
E[X(X-1)] &= \left.\frac{d^2 G_{X}(s)}{d s^2}\right|_{s=1}\\[0.7em]
&= \left. \frac{2p(1-p)^2}{\left\{1-(1-p)s\right\}^3 } \right|_{s=1}\\[0.7em]
&= \frac{2(1-p)^2}{p^2}\\[0.7em]
V[X] &= E[X^2] - E[X]^2\\[0.7em]
&= E[X(X-1)] + E[X] - E[X]^2\\[0.7em]
&= \frac{2(1-p)^2}{p^2} + \frac{1-p}{p} - \frac{(1-p)^2}{p^2}\\[0.7em]
&= \frac{1-p}{p^2}
\end{align}
再生性
再生性を示すためには，再生性を示したい分布に従う独立な二つの確率変数を考え，その和の確率母関数を計算したときに，パラメータが和の形になっていることを示します。
幾何分布は再生性をもちません。なぜなら，幾何分布が「初めて表が出るまでの回数」であるのに対し，「$r$回表が出るまでの失敗の回数」まで拡張した分布は負の二項分布となり，幾何分布に従う独立な二つの変数の和は$r=2$の負の二項分布に従うからです。確率変数の和が別の確率分布に従うときは，再生性を持つとは表現されません。
ロードマップ
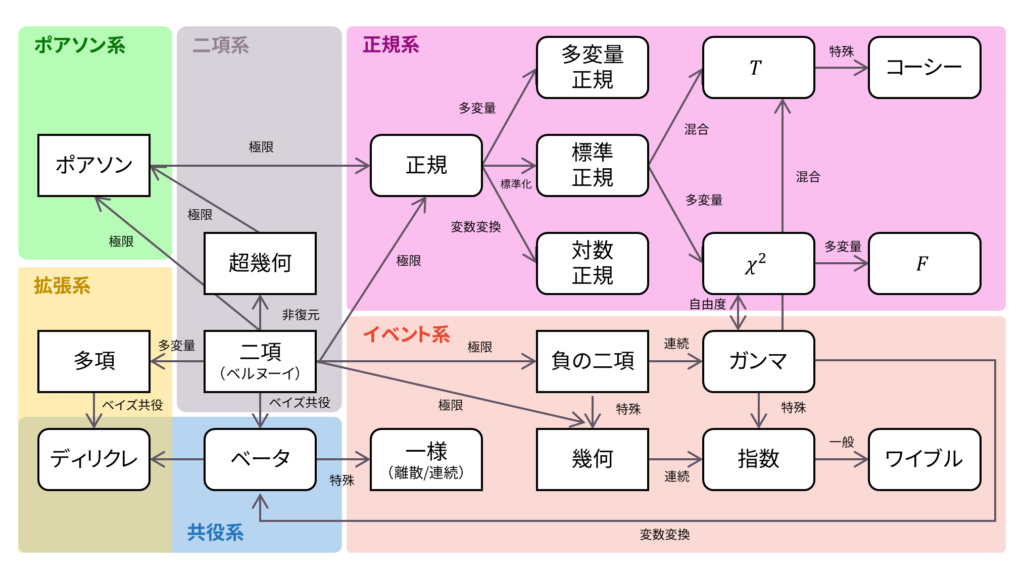
さて，ロードマップに戻りましょう。 幾何分布は，無限に続くベルヌーイ試行として定義されました。以下の内容も参考になるでしょう。
参考文献
本稿の執筆にあたり参考にした文献は，以下でリストアップしております。
コメント