本記事は「これなら分かる!はじめての数理統計学」シリーズに含まれます。
不適切な内容があれば,記事下のコメント欄またはお問い合わせフォームよりご連絡下さい。
本記事の流れ
本書のロードマップに登場する確率分布を総まとめします。
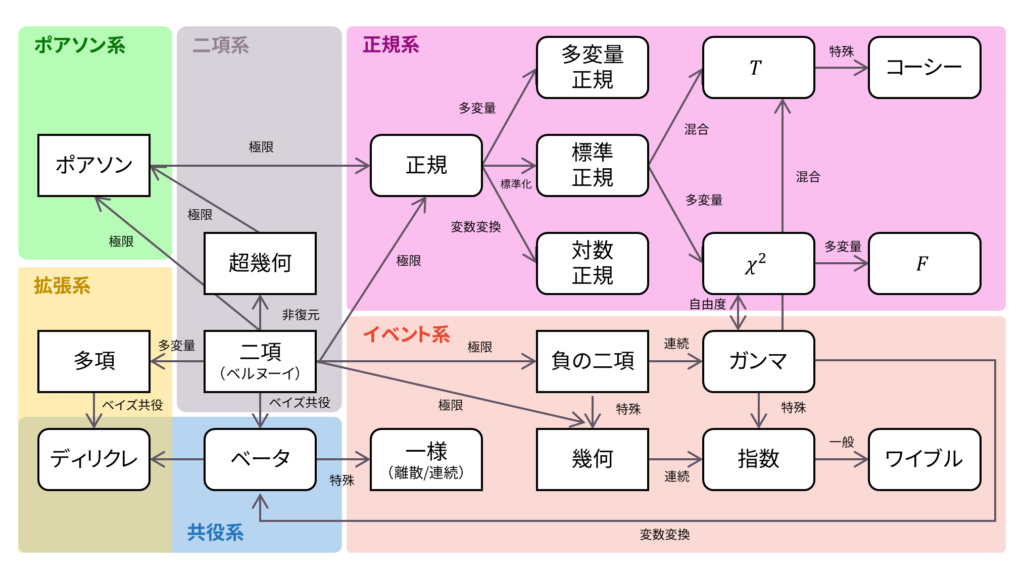
具体的には,以下の特徴をまとめていきます。証明は別ページで行っていきます。
- 確率質量関数/確率密度関数
- 確率母関数/モーメント母関数
- 平均
- 分散
- 再生性
本ページでは,以下の形で確率分布の詳細をお伝えしていきます。
雛形
- 確率質量関数/確率密度関数
- 確率母関数/モーメント母関数
- 期待値
- 分散
[確率分布の説明]
離散一様分布
f_{X}(x) &= \frac{1}{n} \\[0.7em]
G_X(s) &=
\begin{cases}
\displaystyle\frac{s(1-s^{n})}{n(1-s)} & |s| < 1 \\
1 & s = 1
\end{cases} \\[0.7em]
E[X] &= \frac{n + 1}{2} \\[0.7em]
V[X] &= \frac{n^2-1}{12}
\end{align}
全ての事象の起こる確率が等しい分布を一様分布と呼びます。特に,確率変数が離散型の場合は離散一様分布と呼びます。離散一様分布に従う確率変数$X$に対し,実現値は
x \in \{0, \ldots, n\}
\end{align}
であり,確率母関数の変数は$|s|\leq1$とします。離散一様分布は再生性を持たず,ロードマップ中ではベータ分布の特殊な場合に相当します。
ベルヌーイ分布
f_{X}(x) &= p^x(1-p)^{1-x} \\[0.7em]
G_{X}(s) &= ps + 1-p \\[0.7em]
E[X] &= p \\[0.7em]
V[X] &= p(1-p)
\end{align}
取り得る結果が成功・失敗の$2$つである試行の結果を表す確率分布をベルヌーイ分布と呼びます。成功する確率を$p \in (0,1)$とおくと,ベルヌーイ分布は以下のように表されます。
\mathrm{Bernoulli}(p)
\end{align}
ベルヌーイ分布に従う確率変数$X$に対し,実現値は
x \in \{0, 1\}
\end{align}
であり,$0$が失敗,$1$が成功を表しているものとします。 また,確率母関数の変数は$|s|\leq 1$とします。ベルヌーイ分布は再生性を持ち,ロードマップ中では二項分布において試行回数が$1$回という特殊な場合に相当します。
二項分布
f_{X}(x) &= {}_n C _x~p^x(1-p)^{n-x} \\[0.7em]
G_{X}(s) &= (ps + 1-p)^n \\[0.7em]
E[X] &= np \\[0.7em]
V[X] &= np(1-p)
\end{align}
取り得る結果が成功・失敗の$2$つである独立な試行を繰り返したとき,成功する回数を表す確率分布を二項分布と呼びます。独立なベルヌーイ試行の繰り返しは二項分布に従いますので,独立な確率変数$Y_1,\ldots,Y_n$が$p\in(0,1)$で指定される同一ベルヌーイ分布に従っているとき,確率変数
X &= Y_1+\cdots+Y_n
\end{align}
の従う分布が二項分布であり,
\Bin(n, p)
\end{align}
と書きます。 二項分布に従う確率変数$X$に対し,実現値は
x \in \{0, \ldots, n \}
\end{align}
であり,確率母関数の変数は$|s|\leq 1$とします。二項分布は再生性を持ち,ロードマップ中ではあらゆる分布の出発点に相当します。
ポアソン分布
f_{X}(x) &= \frac{\lambda^x}{x!}e^{-\lambda} \\[0.7em]
G_{X}(s) &= e^{\lambda(s-1)} \\[0.7em]
E[X] &= \lambda \\[0.7em]
V[X] &= \lambda
\end{align}
二項分布$\Bin(n,p)$において,$np=\lambda>0$を一定に保ったまま$n$を大きくしていくとポアソン分布
\Po (\lambda)
\end{align}
が得られます。ポアソン分布に従う確率変数$X$に対し,実現値は
x &\in \{0, \ldots, n \}
\end{align}
であり,確率母関数の変数は$|s|\leq1$とします。ポアソン分布は再生性を持ち,ロードマップ中では二項分布の極限に相当します。
超幾何分布
f_{X}(x) &= \frac{{}_M \tilde{\C}_{x} \times {}_{N-M} \tilde{\C}_{n-x}}{{}_N \C_n} \\[0.7em]
E[X] &= np \\[0.7em]
V[X] &= \frac{N-n}{N-1} np(1-p)
\end{align}
ただし,$p=M/N$であり,$\tilde{C}$は二項係数を拡張した記号である。
{}_N \tilde{C} _x &=
\begin{cases}
{}_N \C_x & (x=0,\cdots,n)\\[0.7em]
0 & (\text{その他})
\end{cases}
\end{align}
アタリが$M$個,ハズレが$N-M$個入っているくじ引きから$n$個を引くとき,アタリの個数$X$は超幾何分布に従います。超幾何分布に従う確率変数$X$に対し,実現値は
x \in \{0, \ldots, n\}
\end{align}
であり,確率母関数の変数は$|s|\leq 1$とします。超幾何分布は再生性を持たず,ロードマップ上では二項分布を非復元抽出として拡張した場合に相当します。なお,超幾何分布の確率母関数は計算が面倒なので割愛されることが多く,本稿もそれに従います。
幾何分布
f_{X}(x) &= p(1-p)^x \\[0.7em]
G_{X}(s) &= \frac{p}{1-(1-p)s} \\[0.7em]
E[X] &= \frac{1-p}{p}\\[0.7em]
V[X] &= \frac{1-p}{p^2}
\end{align}
無限に続くベルヌーイ試行において,成功するまでの失敗の回数$X$は幾何分布に従います。幾何分布に従う確率変数$X$に対し,実現値は
x\in\{0, \ldots, n\}
\end{align}
であり,確率母関数の変数は$|s|\leq 1$とします。幾何分布は再生性を持たず,ロードマップ中では負の二項分布の特殊な場合に相当します。
負の二項分布
f_{X}(x) &= {}_{x+r-1} C_{x}\;p^r (1-p)^{x} \\[0.7em]
G_{X}(s) &= \left\{ \frac{p}{1-(1-p)s} \right\}^r \\[0.7em]
E[X] &= r\frac{1-p}{p} \\[0.7em]
V[X] &= r \frac{1-p}{p^2}
\end{align}
無限に続くベルヌーイ試行において,$r$回成功するまでの失敗の回数$X$は負の二項分布
\NB (r, p)
\end{align}
に従います。ただし,$r \in \bbN$,$p \in [0, 1]$とします。負の二項分布に従う確率変数$X$に対し,実現値は
x_k \in \{0, 1, \ldots \}
\end{align}
であり,確率母関数の変数は$|s_k|\leq 1$とします。負の二項分布は再生性を持ち,ロードマップ中では負の二項分布は二項分布の極限に相当します。なお,負の二項分布はポアソン分布の混合分布としても定義されます。
多項分布
f_{\mX}(\vx) &= \frac{n!}{x_1!\cdots x_K!}~p_1^{x_1}\cdots p_K^{x_K} \\[0.7em]
G_{\mX}(\vs) &= (p_1s_1 + \cdots + p_{K-1}s_{K-1} + p_K)^n \\[0.7em]
E[X_i] &= np_i \\[0.7em]
V[X_i] &= np_i(1-p_i)
\end{align}
二項分布を複数のカテゴリに拡張した分布を多項分布と呼びます。ただし,毎回の試行で各カテゴリーの発生確率を$p_1,\cdots,p_K$とし,これらは
p_1+\cdots+p_K &= 1
\end{align}
を満たします。$K-1$個の確率が決まった時点であと$1$つの確率も決まってしまうため,自由に定められる確率変数は$X_1,\ldots, X_{K-1}$の$K-1$個になります。また,多項分布では実現値$x$と確率母関数の変数$s$も$K-1$個用意しなくてはなりません。簡単のため,確率質量関数と確率母関数は,以下の長さ$K$のベクトルを用いて表します。
\mX &= [ X_1, \ldots, X_K ] \\[0.7em]
\vx &= [x_1, \ldots, x_K] \\[0.7em]
\vs &= [s_1, \ldots, s_K]
\end{align}
ただし,自由度は$K-1$であることに注意してください。多項分布に従う確率変数$X_k$に対し,実現値は
x_k \in \{0, \ldots, n\}
\end{align}
であり,確率母関数の変数は$|s_k|\leq 1$とします。多項分布は再生性を持たず,ロードマップ中では二項分布の多変量拡張に相当します。
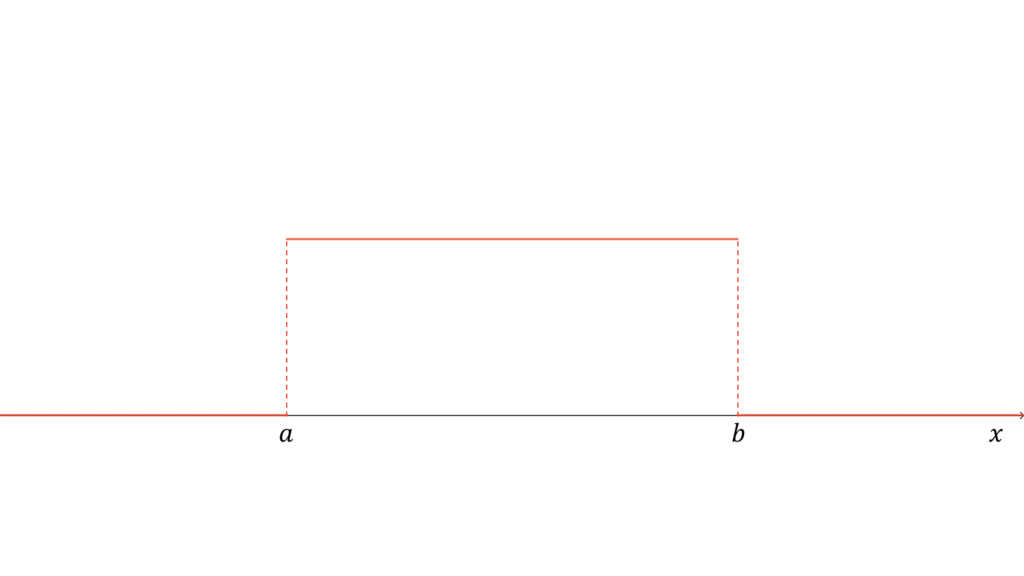
連続一様分布
f_{X}(x) &= \frac{1}{b-a} \\[0.7em]
M_{X}(t) &=
\begin{cases}
\displaystyle \frac{e^{tb}-e^{ta}}{t(b-a)} & t \neq 0 \\[0.7em]
1 & t = 0
\end{cases} \\[0.7em]
E[X] &= \frac{b+a}{2}\\[0.7em]
V[X] &= \frac{(b-a)^2}{12}
\end{align}
全ての事象の起こる確率が等しい分布を一様分布と呼びます。特に,確率変数が連続型の場合は連続一様分布と呼び,
U(a, b)
\end{align}
と表します。ただし,$a \in \bbR$,$b \in \bbR$,$a \neq b$とします。連続一様分布に従う確率変数$X$に対し,実現値は
x \in [a, b]
\end{align}
であり,モーメント母関数の変数は$t \in \bbR$とします。連続一様分布は再生性を持たず,ロードマップ中ではベータ分布の特殊な場合に相当します。
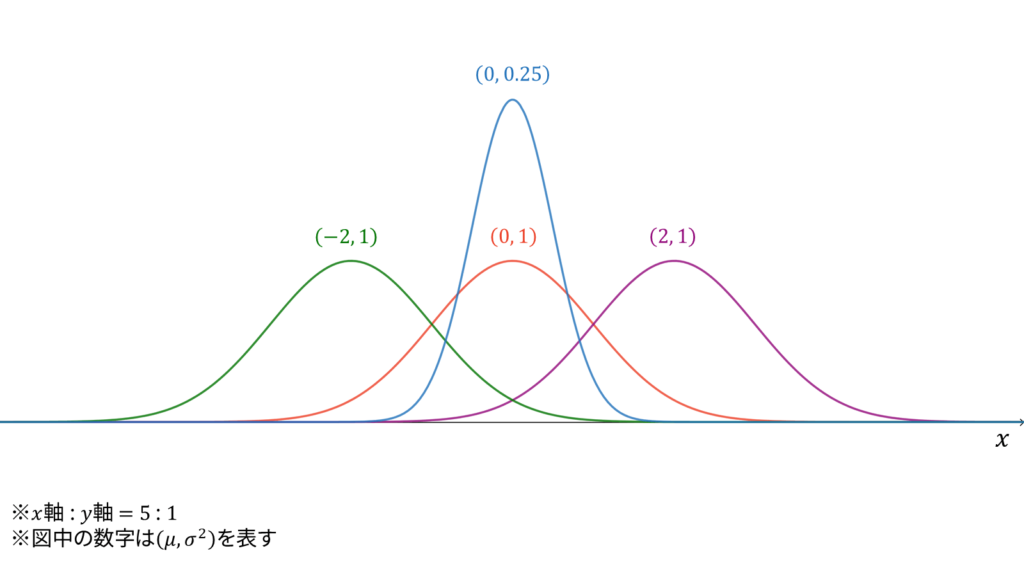
正規分布
f_{X}(x) &= \frac{1}{\sqrt{2\pi\sigma^2}}\exp\left\{ -\frac{1}{2\sigma^2} (x-\mu)^2 \right\} \\[0.7em]
M_{X}(t) &= \exp \left( \mu t + \frac{1}{2}\sigma^2t^2 \right) \\[0.7em]
E[X] &= \mu \\[0.7em]
V[X] &= \sigma^2
\end{align}
二項分布$\Bin (n, p)$において,$p$を一定に保ったまま$n$と$x$を大きくしていくと,正規分布
\N (\mu, \sigma^2)
\end{align}
が得られます。正規分布に従う確率変数$X$に対し,実現値は
x \in \bbR
\end{align}
であり,モーメント母関数の変数は$t \in \bbR$とします。正規分布は再生性を持ち,ロードマップ中では二項分布とポアソン分布の極限に相当します。同時に,正規分布は「正規系」の源流となる分布です。直感的には,二項分布の連続拡張が正規分布です。
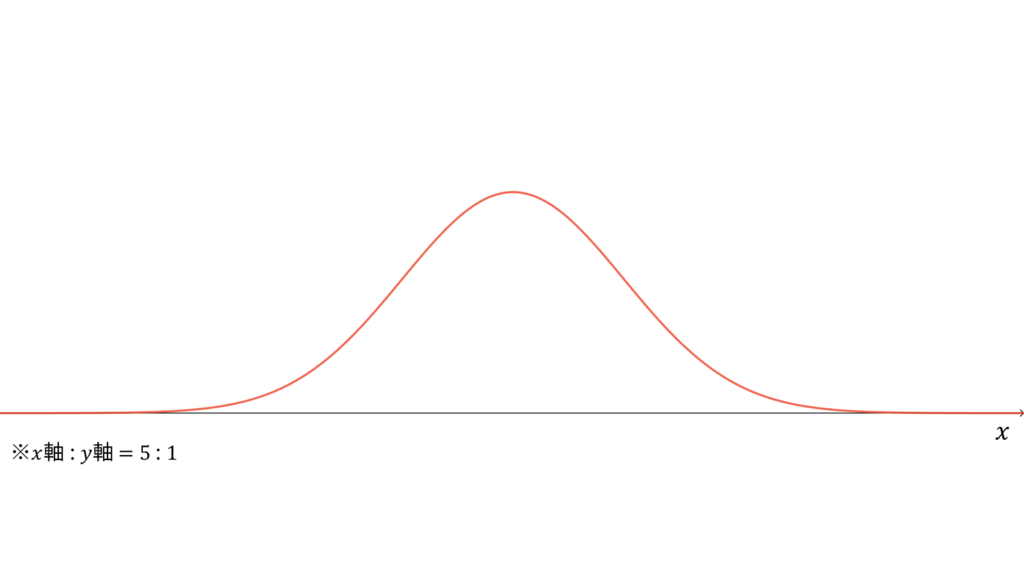
標準正規分布
f_{X}(x) &= \frac{1}{\sqrt{2\pi}}\exp\left( -\frac{1}{2} x^2 \right) \\[0.7em]
M_{X}(t) &= \exp \left(\frac{1}{2}t^2 \right) \\[0.7em]
E[X] &= 0 \\[0.7em]
V[X] &= 1
\end{align}
正規分布$\N (\mu, \sigma^2)$に従う確率変数$X$対して,
Z &= \frac{X-\mu}{\sigma}
\end{align}
が従う分布$\N (0, 1)$を標準正規分布と呼びます。標準正規分布に従う確率変数$X$に対し,実現値は
x \in \bbR
\end{align}
であり,モーメント母関数の変数は$t \in \bbR$とします。標準分布は再生性を持ち,ロードマップ中では正規分布を標準化したもの相当します。
対数正規分布
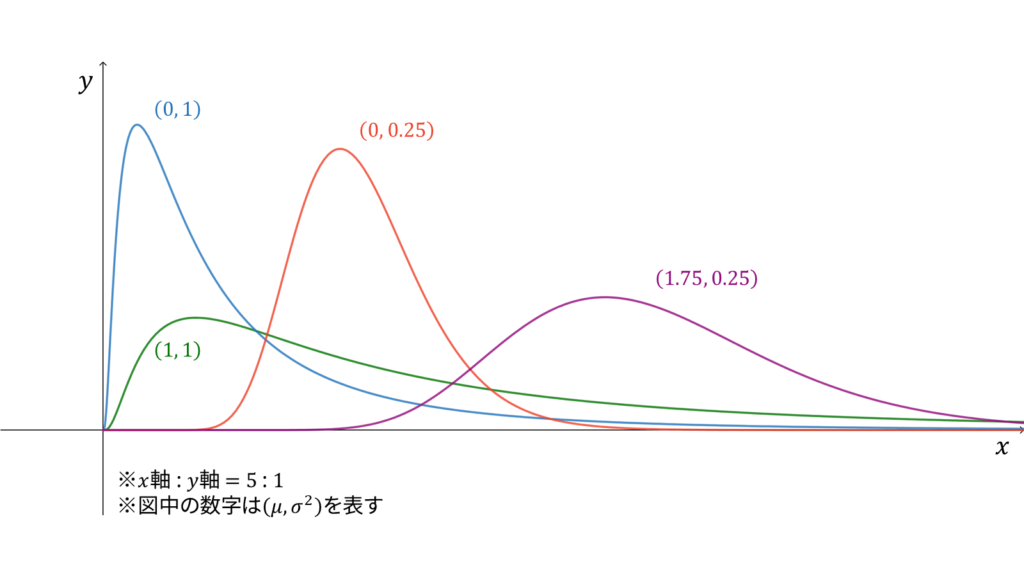
f_{X}(x) &= \frac{1}{\sqrt{2\pi\sigma^2}}\frac{1}{x}\exp\left\{ -\frac{1}{2\sigma^2} (\log x-\mu)^2 \right\} \\[0.7em]
E[X] &= e^{\mu + \sigma^2/2} \\[0.7em]
V[X] &= e^{2\mu + \sigma^2}\left( e^{\sigma^2}-1 \right)
\end{align}
正規分布$\N (\mu, \sigma^2)$に従う確率変数$Y$対して,
X &= e^{Y}
\end{align}
が従う分布を対数正規分布と呼びます。$\log X$が正規分布に従うことが名前の由来になっています。対数正規分布に従う確率変数$X$に対し,実現値は
x \in \bbR_{+}
\end{align}
であり,モーメント母関数は存在しません。対数正規分布は再生性を持たず,ロードマップ中では正規分布からの変数変換に相当します。注意点として,確率密度関数中の$\mu$と$\sigma^2$は正規分布とは異なり,それぞれ平均と分散には対応しません。
多変量正規分布
f_{\mX}(\vx) &= \frac{1}{(2\pi)^{D/2}|\Sigma|^{1/2}}\exp \left\{ -\frac{1}{2}(\vx-\vmu)^T \Sigma^{-1}(\vx-\vmu) \right\} \\[0.7em]
M_{\mX}(\vt) &= \exp\left( \vmu^T\vt + \frac{1}{2}\vt^T\Sigma\vt \right) \\[0.7em]
E[\mX] &= \vmu \\[0.7em]
V[\mX] &= \Sigma
\end{align}
多変量正規分布は正規分布を$D$次元に多変量化した確率分布であり,以下のベクトル
\mX &= [X_{1}, \ldots, X_{D}] \\[0.7em]
\vmu &= [\mu_{1}, \ldots, \mu_{D}]
\end{align}
と,分散共分散行列$\Sigma \in \bbR^{D \times D}$を用いて定義されます。多変量正規分布に従う確率変数$\mX$に対し,実現値は
\vx \in \bbR^{D}
\end{align}
であり,モーメント母関数の変数は$\vt \in \bbR^{D}$とします。多変量正規分布は再生性を持ち,ロードマップ中では正規分布の多変量化に相当します。
指数分布
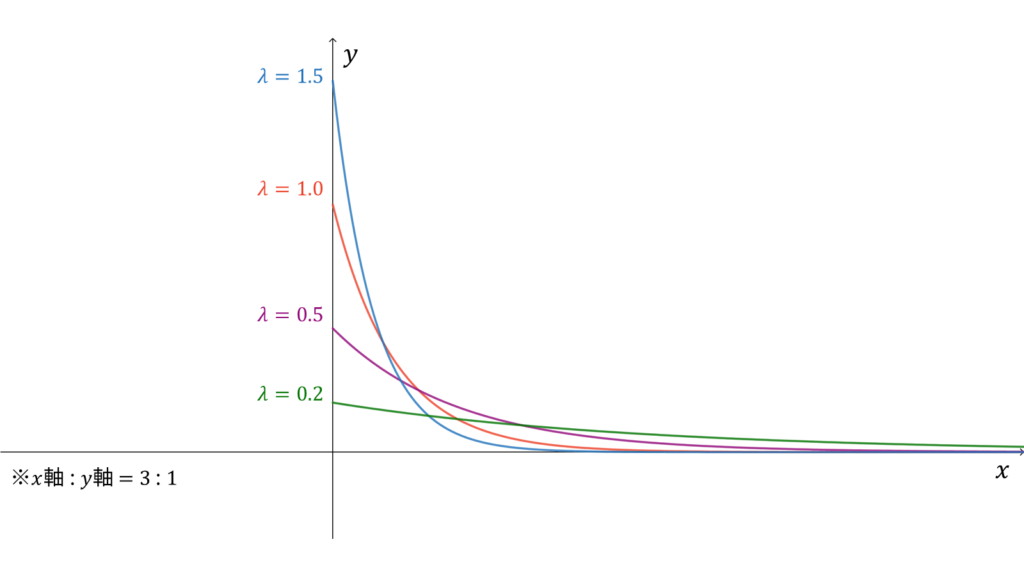
f_{X}(x) &= \lambda e^{-\lambda x} \\[0.7em]
M_{X}(t) &= \frac{1}{1-t/\lambda} \\[0.7em]
E[X] &= \frac{1}{\lambda} \\[0.7em]
V[X] &= \frac{1}{\lambda^2}
\end{align}
指数分布は事象の生起間隔の確率を与え,
\Exp (\lambda)
\end{align}
と表されます。ただし,$\lambda > 0$とします。指数分布に従う確率変数$X$に対し,実現値は
x \in \bbR_{+}
\end{align}
であり,モーメント母関数の変数は$t \in \bbR$とします。指数分布は再生性を持たず,ロードマップ中ではガンマ分布の特殊ケース$\Ga (1, \lambda)$に相当します。
ガンマ分布
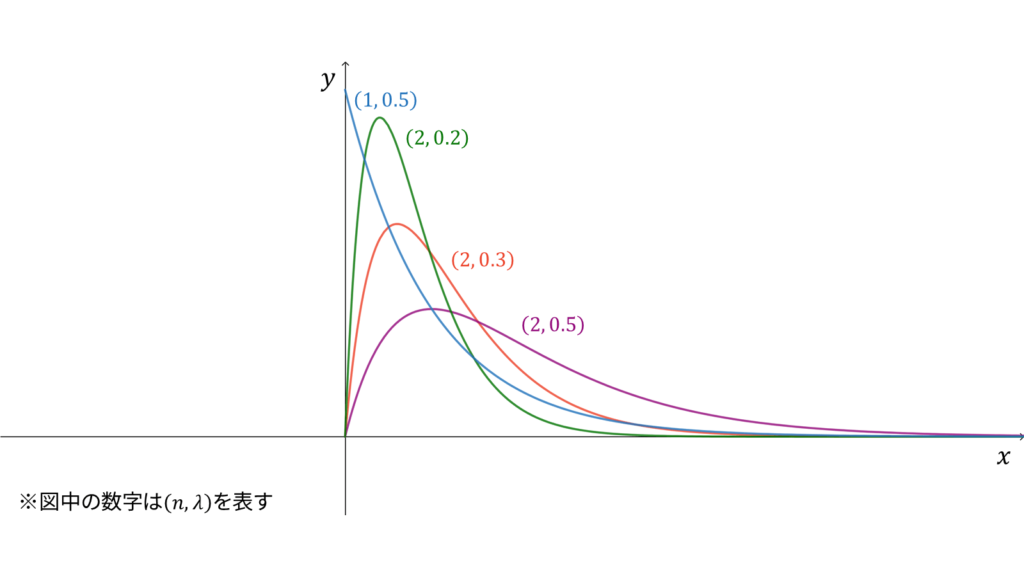
f_{X}(x) &= \frac{\lambda^{n}}{\Gamma(n)}x^{n-1} e^{-\lambda x} \\[0.7em]
M_{X}(t) &= \left( \frac{1}{1-t/\lambda} \right)^{n} \\[0.7em]
E[X] &= \frac{n}{\lambda} \\[0.7em]
V[X] &= \frac{n}{\lambda^2}
\end{align}
ただし,$\Gamma(\cdot)$はガンマ関数を表す。
\Gamma(n) &= \int_0^{\infty}t^{n-1}e^{-t}dt
\end{align}
指数分布に独立に従う確率変数の和が従う分布をガンマ分布と呼び,
\Ga (n, \lambda)
\end{align}
と表します。ただし,$\lambda > 0$とします。ガンマ分布に従う確率変数$X$に対し,実現値は
x \in \bbR_{+}
\end{align}
であり,モーメント母関数の変数は$t < \lambda$とします。ガンマ分布は再生性を持ち,ロードマップ中では指数分布の和に相当すると同時に,負の二項分布の連続拡張に相当します。
ベータ分布
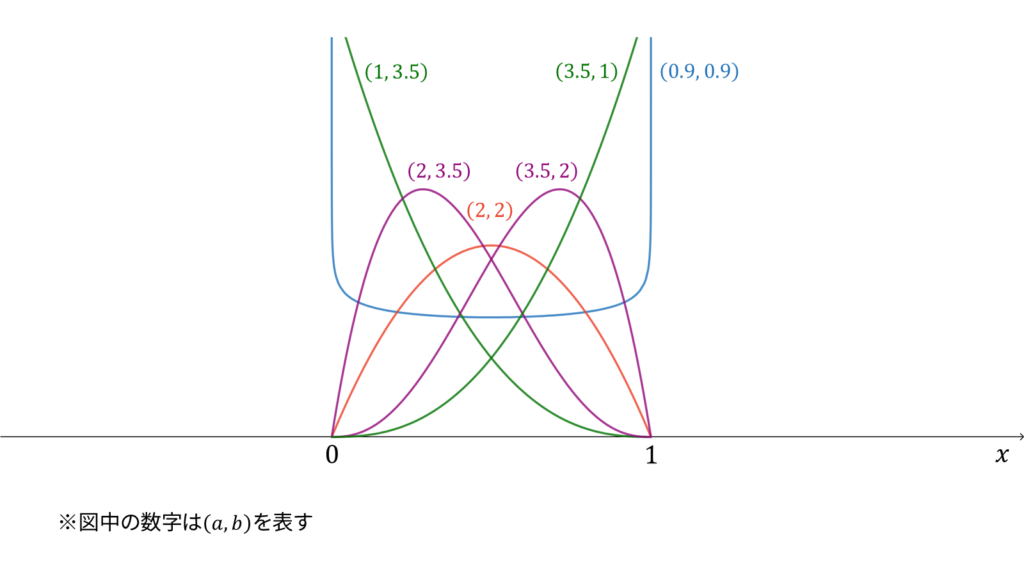
f_{X}(x) &= \frac{1}{B(a, b)}x^{a-1}(1-x)^{b-1} \\[0.7em]
E[X] &= \frac{a}{a+b} \\[0.7em]
V[X] &= \frac{ab}{(a+b)^2(a+b+1)}
\end{align}
ただし,$B(\cdot)$はベータ関数を表す。
B(a, b) &= \int_0^1 x^{a-1}(1-x)^{b-1}dx
\end{align}
ベータ分布は二項分布の共役事前分布として導入され,
\Be (a, b)
\end{align}
と表します。ベータ分布に従う確率変数$X$に対し,実現値は
x \in [0, 1]
\end{align}
であり,モーメント母関数の変数は$t \in \bbR$とします。ベータ分布は再生性を持たず,ロードマップ中では二項分布のベイズ共役に相当しています。ベータ分布は,ガンマ分布に従う確率変数の変数変換を利用しても導くことができます。なお,ベータ分布のモーメント母関数は存在しますが,利用されることが少ないためここでは割愛することにします。
ディリクレ分布
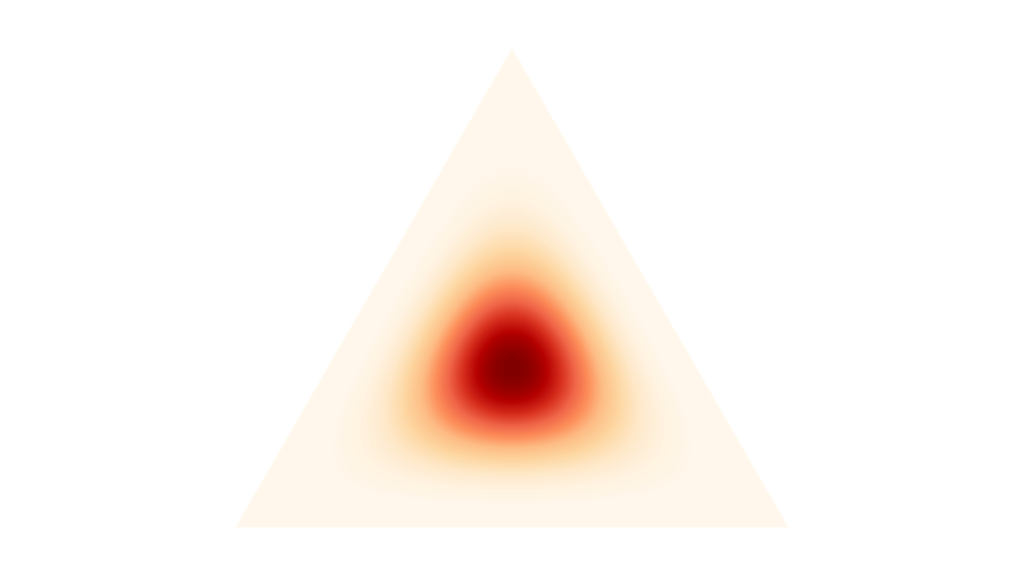
f_{\mX}(\vx) &= \frac{1}{B(\valpha)} \prod_{k=1}^{K} x_{k}^{\alpha_{k}-1} \\[0.7em]
E[X_k] &= \frac{\alpha_k}{\sum_{l=1}^{K} \alpha_l} \\[0.7em]
V[X_k] &= \frac{\alpha_k\left(\sum_{l=1}^{K} \alpha_l-\alpha_k\right)}{\left(\sum_{l=1}^{K} \alpha_l + 1\right)\left(\sum_{l=1}^{K} \alpha_l\right)^2}
\end{align}
ただし,$B(\cdot, \cdot)$はベータ関数を表す。
B(a, b) &= \int_0^1 x^{a-1}(1-x)^{b-1}dx
\end{align}
ディリクレ分布はベータ分布の多カテゴリ拡張であり,
\Dir (\valpha)
\end{align}
と表され,以下のベクトル
\mX &= [X_1, \ldots, X_K] \\[0.7em]
\vx &= [x_1, \ldots, x_K] \\[0.7em]
\valpha &= [\alpha_1, \ldots, \alpha_K]
\end{align}
を用いて定義されます。ただし,$\alpha_k-1\geq 0$は各カテゴリの発生回数を表し,確率変数$\mX$の実現値$\vx$は
\sum_{k=1}^{K} x_k &= 1
\end{align}
を満たします。モーメント母関数は複雑な形をしているため,あまり利用されません。ディリクレ分布は再生性を持たず,ロードマップ中ではベータ分布の多変量化に相当します。すなわち,多項分布の共役事前分布に相当します。
標準コーシー分布
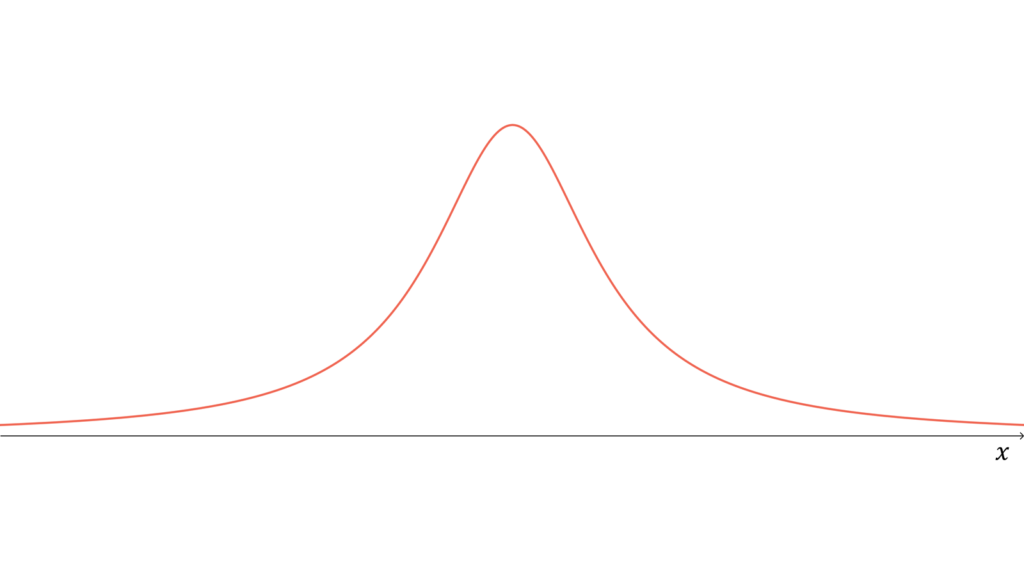
f_{X}(x) &= \frac{1}{\pi}\frac{1}{x^2 + 1} \\[0.7em]
\phi_X(t) &= e^{-|t|}
\end{align}
連続一様分布に従う確率変数
Y \sim U(-\pi/2, \pi/2)
\end{align}
に対して,以下の変数変換
X &= \tan Y
\end{align}
を考えたとき,$X$が従う分布を標準コーシー分布と呼びます。標準コーシー分布に従う確率変数$X$に対し,実現値は
x \in \bbR
\end{align}
であり,期待値・分散・モーメント母関数が定義されません。ただし,特性関数は存在します。標準コーシー分布は再生性を持たず,ロードマップ中では$T$分布の特殊な場合(自由度$1$)に相当します。ただし, 独立に標準コーシー分布に従う確率変数の算術平均に関しては再生性を持ちます。なお,標準コーシー分布は正規分布よりも裾が重い分布として有名です。
ワイブル分布
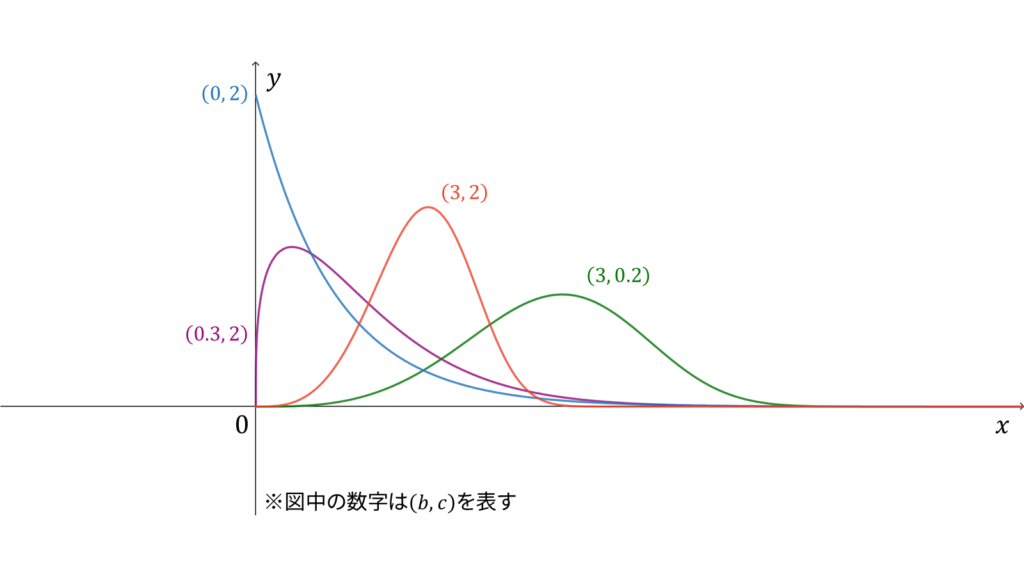
f_{X}(x) &= cx^b \exp \left( -\frac{cx^{b+1}}{b+1} \right) \\[0.7em]
E[X] &= m\Gamma(1 + \kappa) \\[0.7em]
V[X] &= m^2 \left\{ \Gamma(1 + 2\kappa)-\Gamma^2(1+\kappa) \right\}
\end{align}
ただし,$\Gamma(\cdot)$はガンマ関数を表し,
m &= \left( \frac{b+1}{c}\right)^{\kappa}
\end{align}
と置いた。
危険率が$ct^b$となる確率分布をワイブル分布と呼びます。他には,以下で導入される確率変数
Y &= \frac{X^{b+1}}{b+1} \\[0.7em]
&= \kappa X^{\kappa^{-1}}
\end{align}
が指数分布$\Exp (c)$に従うときに,$X$が従う分布がワイブル分布になります。ただし,$\kappa = (b + 1)^{-1}$と置きました。ワイブル分布に従う確率変数$X$に対し,実現値は
x \in \bbR_{+}
\end{align}
であり,モーメント母関数は$e^x$のテイラー展開とガンマ関数の定義を用いて導出されます。ただし,平均と分散は指数分布からの変数変換を用いて求められますので,今回はモーメント母関数は割愛します。ワイブル分布は再生性を持たず,ロードマップ中では指数分布の一般化に相当します。
カイ二乗分布
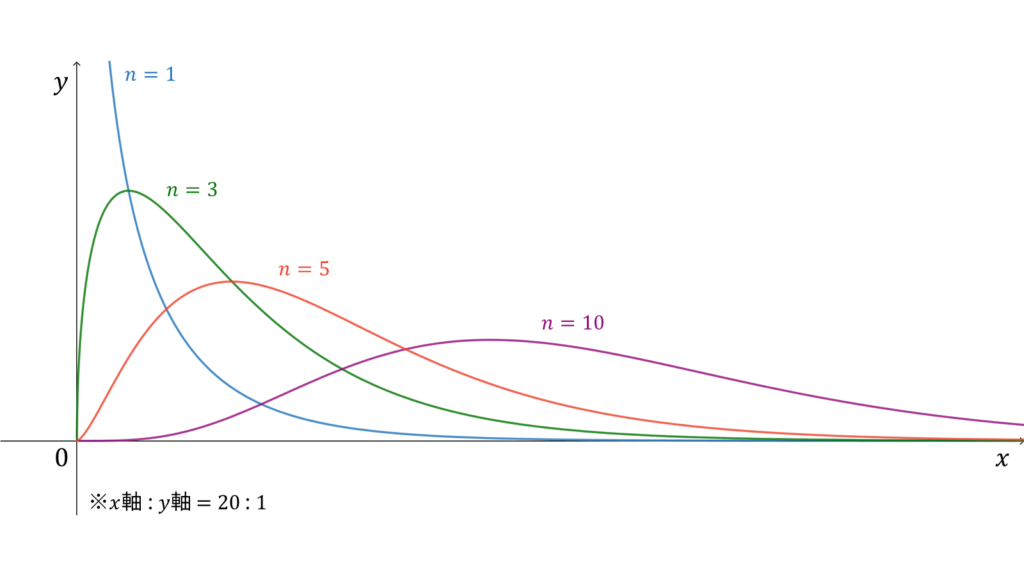
f_{X}(x) &= \frac{x^{n/2-1}e^{-x/2}}{2^{n/2}\Gamma\left( n/2 \right)} \\[0.7em]
M_{X}(t) &= \left( \frac{1}{1-2t} \right)^{n/2} \\[0.7em]
E[X] &= n \\[0.7em]
V[X] &= 2n
\end{align}
ただし,$\Gamma(\cdot)$はガンマ関数を表す。
\Gamma(n) &= \int_0^{\infty}t^{n-1}e^{-t}dt
\end{align}
$Y_1,\ldots,Y_n$が独立に$N(0,1)$に従っているとします。このとき,
X &= Y_1^2 + \cdots + Y_n^2
\end{align}
が従う分布を自由度$n$のカイ二乗分布($\chi^2$分布)と呼び,
\chi^2(n)
\end{align}
と表します。カイ二乗分布に従う確率分布$X$に対し,実現値は
x \in \bbR_{+}
\end{align}
であり,モーメント母関数の変数は$t < 1/2$とします。カイ二乗分布は再生性を持ち,ロードマップ中では標準正規分布の多変量化に相当します。同時に,カイ二乗分布はガンマ分布の特殊な場合にも相当します。
F分布
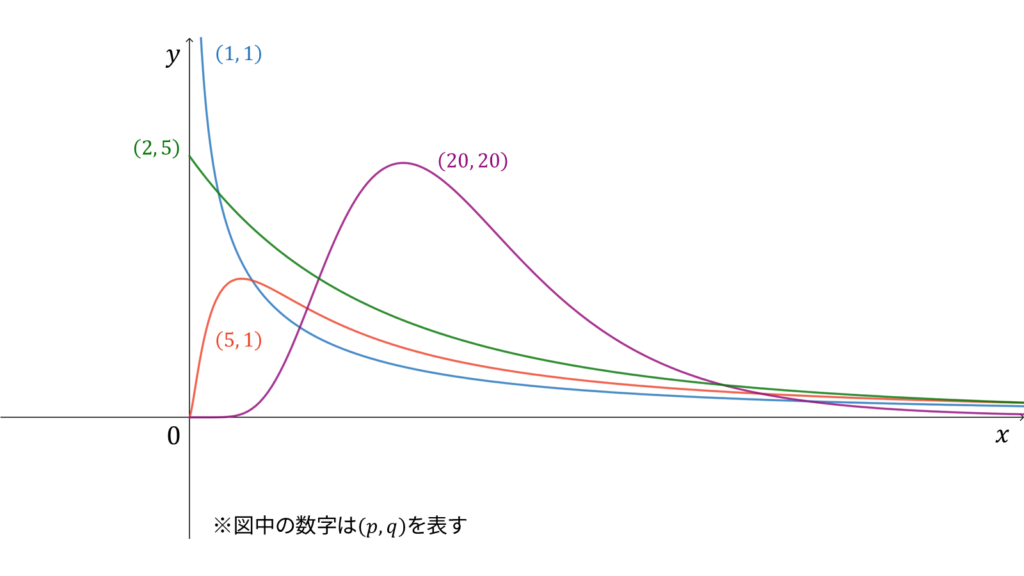
f_{X}(x) &= \frac{p^{p/2}q^{q/2}}{B(p/2, q/2)}\frac{x^{p/2-1}}{(px+q)^{(p+q)/2}} \\[0.7em]
E[X] &= \frac{q}{q-2} \\[0.7em]
V[X] &= 2 \left( \frac{q}{q-2} \right)^2\frac{p+q-2}{p(q-4)}
\end{align}
ただし,$B(\cdot)$はベータ関数を表す。
B(a, b) &= \int_0^1 x^{a-1}(1-x)^{b-1}dx
\end{align}
以下で定義される独立な確率変数
U\sim \chi^2(p) \\[0.7em]
V\sim \chi^2(q)
\end{align}
に対し,確率変数
X &= \frac{U/p}{V/q}
\end{align}
が従う確率分布を自由度$(p,q)$の$F$分布と呼び,
F(p, q)
\end{align}
と表します。$F$分布に従う確率変数$X$に対し,実現値は
x \in \bbR_{+}
\end{align}
であり,モーメント母関数は存在しません。$F$分布は再生性を持たず,ロードマップ中ではカイ二乗分布の多変量化に相当します。
t分布
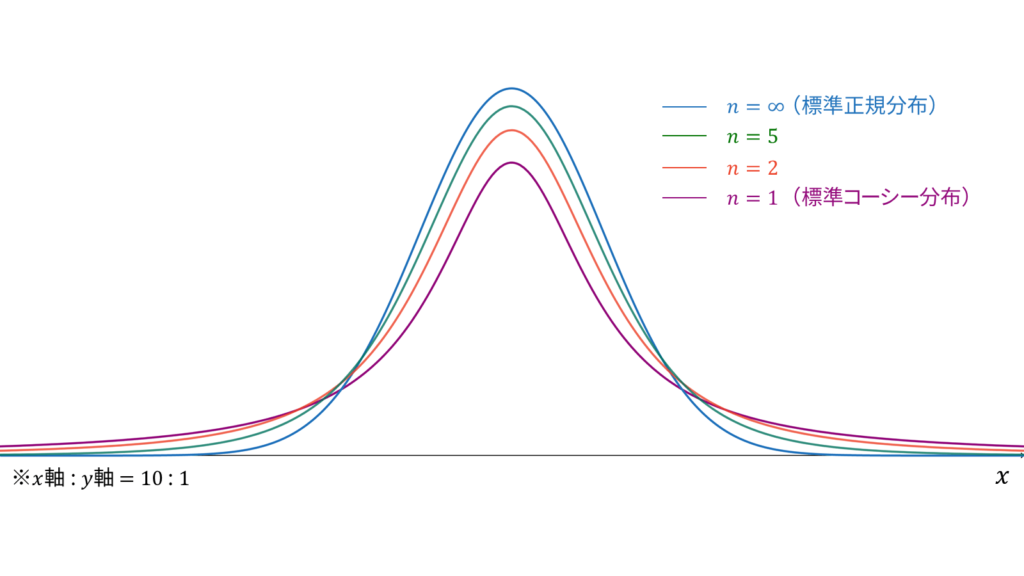
f_{X}(x) &= \frac{1}{\sqrt{n}B(n/2, 1/2)}\left( 1+\frac{x^2}{n} \right)^{-(n+1)/2} \\[0.7em]
E[X] &= 0 && (n > 1)\\[0.7em]
V[X] &= \frac{n}{n-2}&&(n > 2)
\end{alignat}
ただし,平均は$n>1$のときに限り存在し,分散は$n>2$のときに限り存在する。また,$B(\cdot)$はベータ関数を表す。
B(a, b) &= \int_0^1 x^{a-1}(1-x)^{b-1}dx
\end{align}
以下で定義される独立な確率変数
Z &\sim N(0,1) \\[0.7em]
W &\sim \chi^2(n)
\end{align}
に対し,確率変数
X &= \frac{Z}{\sqrt{W/n}}
\end{align}
が従う分布を自由度$n$のt分布と呼び,
t(n)
\end{align}
と表します。t分布に従う確率変数$X$に対し,実現値は
x \in \bbR
\end{align}
であり,モーメント母関数は存在しません。t分布は再生性を持たず,ロードマップ中では標準正規分布とカイ二乗分布の混合分布に相当します。
ロードマップ外の確率分布
惜しくもロードマップに含めることができなかった主な確率分布を紹介します。
標準ロジスティック分布
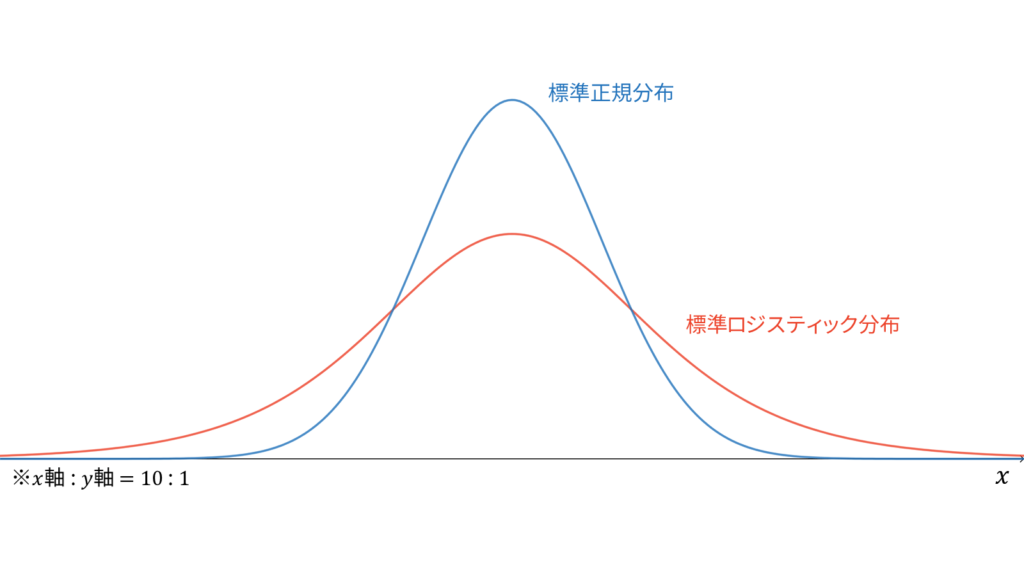
f_{X}(x) &= \frac{e^{-x}}{\left(1+e^{-x}\right)^2} \\[0.7em]
M_{X}(t) &= \Gamma(1+t) \Gamma(1-t) \\[0.7em]
E[X] &= 0 \\[0.7em]
V[X] &= \frac{\pi^2}{3}
\end{align}
ただし,$\Gamma(\cdot)$はガンマ関数を表す。
\Gamma(n) &= \int_0^{\infty}t^{n-1}e^{-t}dt
\end{align}
標準ロジスティック分布は,累積分布関数が標準シグモイド関数となる確率分布として定式化されます。標準ロジスティック分布に従う確率変数$X$に対し,実現値は
x \in \bbR
\end{align}
であり,モーメント母関数の変数は$|t|<1$とします。正規分布とよく似た形をしていますが,より裾の長い分布になっています。
ゴンぺルツ分布
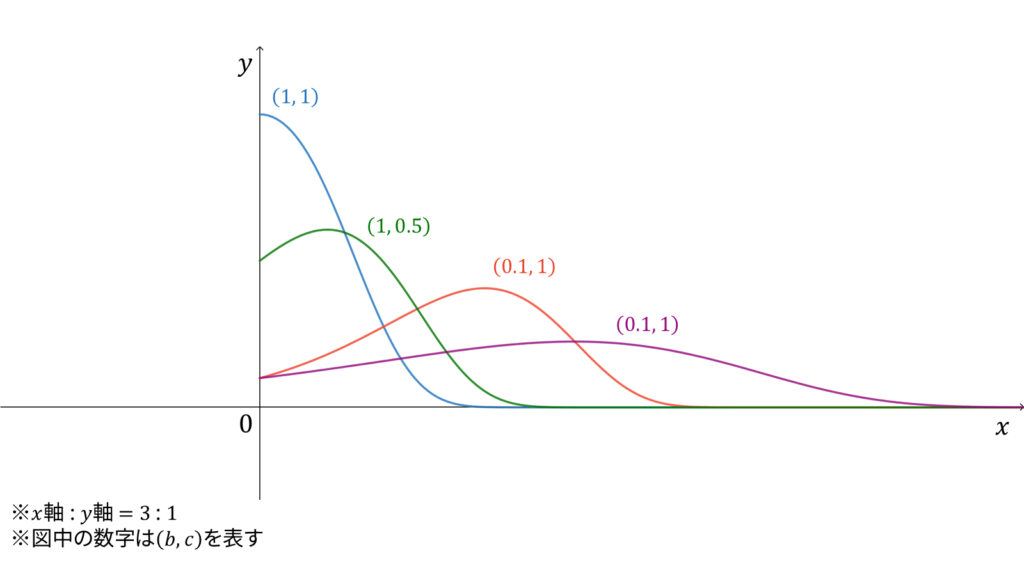
f_{X}(x) &= c\exp\left( bx-\frac{c}{b}e^{bx} + \frac{c}{b} \right)
\end{align}
ゴンぺルツ(Gompertz)分布は,危険率が$ce^{bx}$である確率分布として導入されます。ゴンぺルツ分布に従う確率変数$X$に対し,実現値は
x \in \bbR_{+}
\end{align}
であり,モーメント母関数・平均・分散は複雑なので割愛します。
ラプラス分布
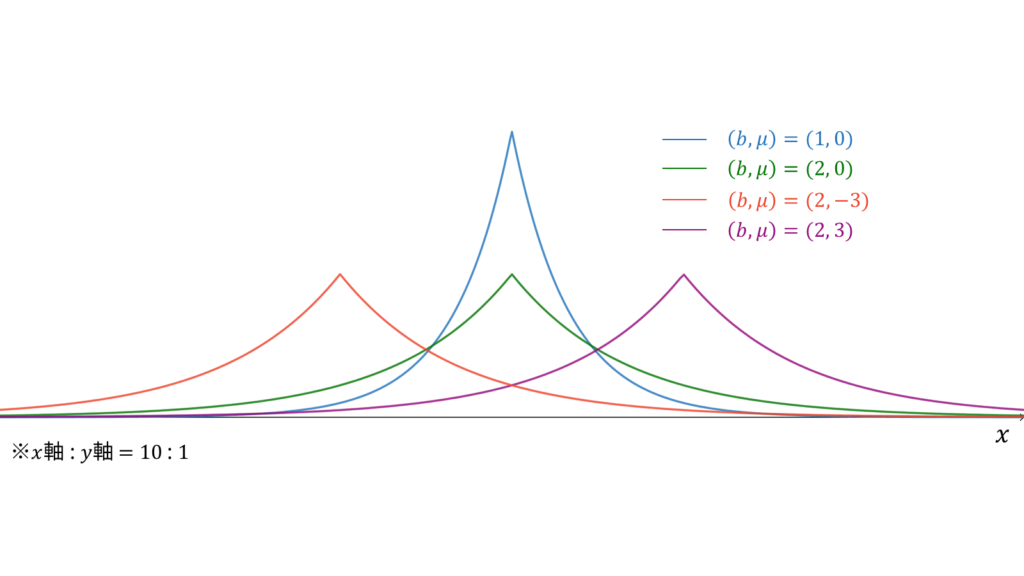
f_{X}(x) &= \frac{1}{2b} \exp\left( -\frac{|x-\mu|}{b} \right) \\[0.7em]
M_{X}(t) &= \frac{e^{\mu t}}{1-b^2 t^2} \\[0.7em]
E[X] &= \mu \\[0.7em]
V[X] &= 2b^2
\end{align}
ラプラス分布は両側(二重)指数分布とも呼ばれ,指数分布を$y$軸に関して対称に貼り付けたような確率密度関数を持ちます。ラプラス分布に従う確率変数$X$に対し,実現値は
x \in \bbR
\end{align}
であり,モーメント母関数の変数は$|t| < 1/b$とします。概形は正規分布に似ていますが,頂点が正規分布よりも尖っています。
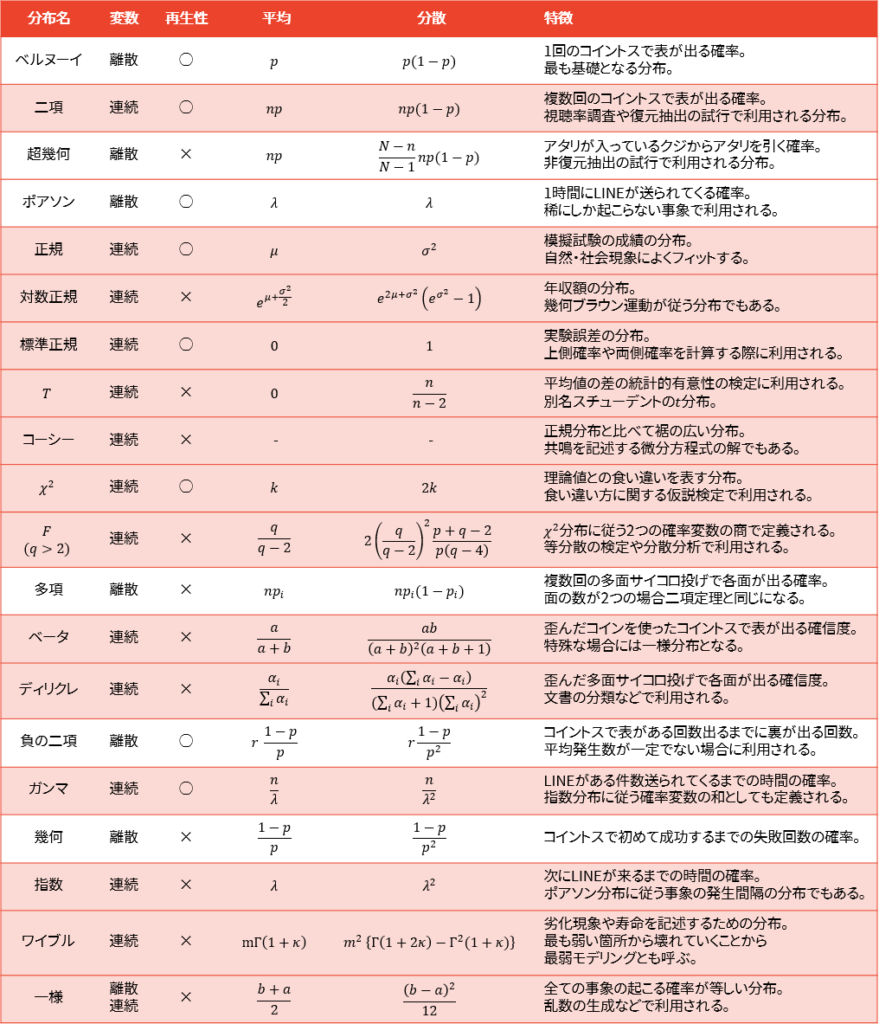
一覧表
最後に一覧表を確認します。赤く塗られている行は連続型確率変数をとる分布を表しています。
参考文献
本稿の執筆にあたり参考にした文献は,以下でリストアップしております。


コメント
コメント一覧 (4件)
ポアソン分布は、イベント系の分布だと考えているのですが、どうのような見解でしょうか。
また、数式では連続していませんが、サンプル数が増えるにつれ、二項分布、ポアソン分布、ワイブル分布、正規分布と変化すると考えています。
これらの境界となるサンプル数を決める事は可能でしょうか。
安原様
ご質問ありがとうございます。
>ポアソン分布は、イベント系の分布だと考えているのですが、どうのような見解でしょうか。
まず前提として、確率分布の「意味」は排反ではないため、綺麗に区分けすることは不可能です。確率分布の区分けを可視化することにネガティブな意見を持たれる方もいます。私が作成した図は、あくまでも確率分布間の関係性の一部を切り取ったものに過ぎません。このような背景から、ポアソン分布はイベント系に区分けされるという考えもあると思います。私個人としては、コイントスという試行と稀にしか起こらない事象は分けたいという考えがありました。逆に言うと、一様分布がイベント系なのも合理的な説明は難しいです。
>数式では連続していませんが、サンプル数が増えるにつれ、二項分布、ポアソン分布、ワイブル分布、正規分布と変化すると考えています。これらの境界となるサンプル数を決める事は可能でしょうか。
恐れ入りますが,私の勉強不足で明確な解答ができません。ご質問の内容は,統計学で非常に重要なトピックです。特に,中心極限定理を認める立場を取る場合,サンプルサイズをどの程度担保すれば正規分布で近似できるのか,というのは多くの人にとって興味のあるトピックだと思っております。一般的には$n=30$や$n=100$と言われることが多い印象がありますが,これらの値を安直に受け入れるべきではありません。統計学の漸近性に関する理論に関しては,今後当サイトにて解説を追加する予定ですので,私の勉強時間も含め,今しばらくお待ちいただけますと幸いです。
p.s.
サンプル数ではなくサンプルサイズのことを意図していると勝手に解釈してしまいました。
分かりやすい記事を書いてくださり、ありがとうございます。特にロードマップにより全体像が把握できるので、理解したものを頭に入れやすいです。
ロードマップによると、「二項分布→(極限)負の二項分布」とあるので、二項分布を負の二項分布に近似できると思うのですが、どのようにするのでしょうか?
星波様
ご質問ありがとうございます。二項分布と負の二項分布の関係性に関しては,下記記事の再生性に関する部分をご覧ください。
https://academ-aid.com/statistics/neg-bin
これでも疑問が晴れなければ,またご質問下さい。よろしくお願いします。