本記事は「これなら分かる!はじめての数理統計学」シリーズに含まれます。
不適切な内容があれば,記事下のコメント欄またはお問い合わせフォームよりご連絡下さい。
目次
ゴンぺルツ分布
\begin{align}
f_{X}(x) &= c\exp\left( bx-\frac{c}{b}e^{bx} + \frac{c}{b} \right)
\end{align}
f_{X}(x) &= c\exp\left( bx-\frac{c}{b}e^{bx} + \frac{c}{b} \right)
\end{align}
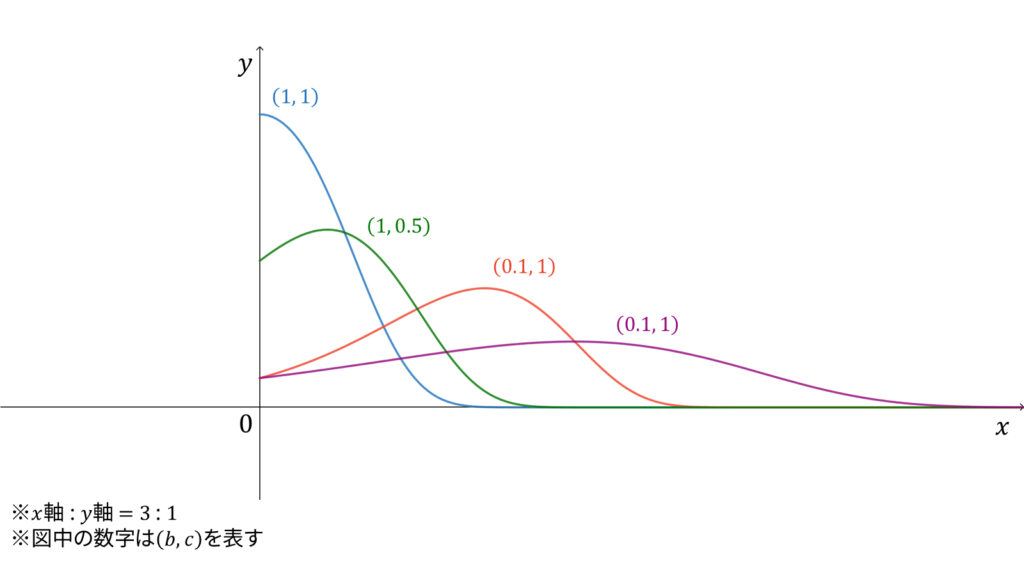
ゴンぺルツ(Gompertz)分布は,危険率が$ce^{bx}$である確率分布として導入されます。ゴンぺルツ分布に従う確率変数$X$に対し,実現値は
\begin{align}
x \in \bbR_{+}
\end{align}
x \in \bbR_{+}
\end{align}
であり,モーメント母関数・平均・分散は複雑なので割愛します。
確率密度関数
ゴンぺルツ分布は,危険率が$l(t)=ce^{bt}$で与えられる確率分布として定式化されます。危険率に基づく確率密度関数の導出より,危険率を$l(\cdot)$とおくと,確率密度関数$f$は以下のように表されるのでした。
\begin{align}
f(t) &= -\frac{d}{dt} \exp\left(-\int_{0}^{t}l(u)du \right)
\end{align}
f(t) &= -\frac{d}{dt} \exp\left(-\int_{0}^{t}l(u)du \right)
\end{align}
$l(t)=ce^{bt}$を代入します。
\begin{align}
f(t) &= -\frac{d}{dt} \exp\left(-\int_{0}^{t} ce^{bu} du \right)\\[0.7em]
&= -\frac{d}{dt} \exp\left(-\frac{c}{b}e^{bt} + \frac{c}{b} \right) \\[0.7em]
&= -\frac{d}{dt}\left( -\frac{c}{b}e^{bt} \right)\cdot \exp\left(-\frac{c}{b}e^{bt} + \frac{c}{b}\right) \\[0.7em]
&= c\exp\left( bt - \frac{c}{b}e^{bt} + \frac{c}{b} \right)
\end{align}
f(t) &= -\frac{d}{dt} \exp\left(-\int_{0}^{t} ce^{bu} du \right)\\[0.7em]
&= -\frac{d}{dt} \exp\left(-\frac{c}{b}e^{bt} + \frac{c}{b} \right) \\[0.7em]
&= -\frac{d}{dt}\left( -\frac{c}{b}e^{bt} \right)\cdot \exp\left(-\frac{c}{b}e^{bt} + \frac{c}{b}\right) \\[0.7em]
&= c\exp\left( bt - \frac{c}{b}e^{bt} + \frac{c}{b} \right)
\end{align}
モーメント母関数
ゴンぺルツ分布のモーメント母関数は複雑な形をしているため,割愛します。
平均・分散
ゴンぺルツ分布の平均・分散は複雑な形をしているため,割愛します。
再生性
再生性を示すためには,再生性を示したい分布に従う独立な二つの確率変数を考え,その和のモーメント母関数を計算したときに,パラメータが和の形になっていることを示します。上でお伝えした通り,ゴンぺルツ分布のモーメント母関数は複雑な形をしており,モーメント母関数の積を考えても同じ関数の形に帰着しないため,ゴンぺルツ分布に再生性はありません。
ロードマップ
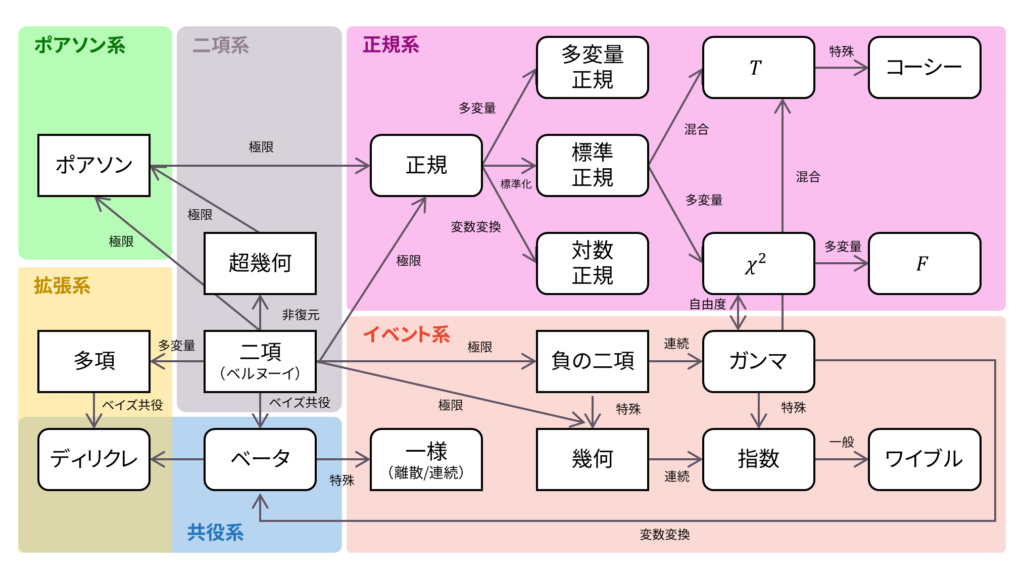
ゴンぺルツ分布はロードマップには含まれていませんが,危険率が$ce^{bt}$となる確率分布として導出されました。以下の内容も参考になるでしょう。
参考文献
本稿の執筆にあたり参考にした文献は,以下でリストアップしております。


コメント