本記事は「これなら分かる!はじめての数理統計学」シリーズに含まれます。
不適切な内容があれば,記事下のコメント欄またはお問い合わせフォームよりご連絡下さい。
マクロな視点
統計学の勉強をしていると,たいていの人は出てくる確率分布の多さに嫌気がさしてしまうと思います。挙げ句の果てには$F$分布の定義などを覚えさせられて,確率分布などよく理解しないままに検定パートに突入です。本資料では,そのような事態を避けるべく,まずはマクロな視点で種々の確率分布を眺めてみたいと思います。
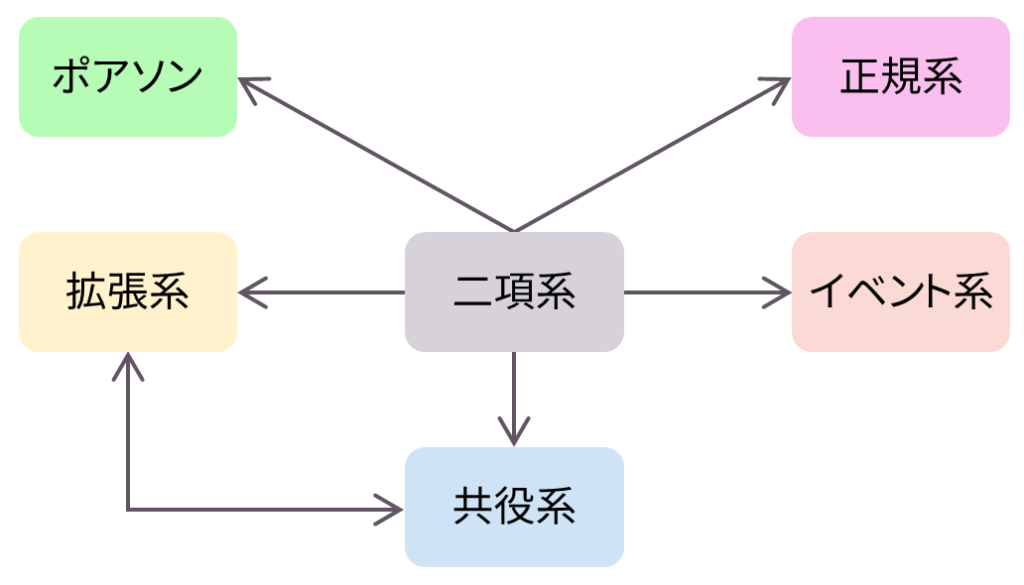
まず,大事な観点として「二項分布から出発させる」というものがあります。種々の確率分布を統一的にまとめる方法は流派がありますが,筆者は二項分布を源流としてそこから流れる川を考えていく方法が最も理解しやすいと感じています。具体的には,上図のようなマクロな視点で二項分布からの流れを捉えてください。
真ん中に位置する「二項系」には,コイントスやなどの試行を表すような確率分布が含まれます。そこから,サイコロ投げなどに「拡張」する流れ,事前分布として「ベイズ共役」を考える流れ,滅多に起こらない事象に対して「ポアソン分布」を考える流れ,自然界によく起こる「正規分布」を持ち出す流れ,そしてある「イベント」の発生に関する分布を考える流れがあります。以下で説明するように,実際には「拡張系」と「共役系」の共通領域に相当する確率分布もあります。
ミクロな視点
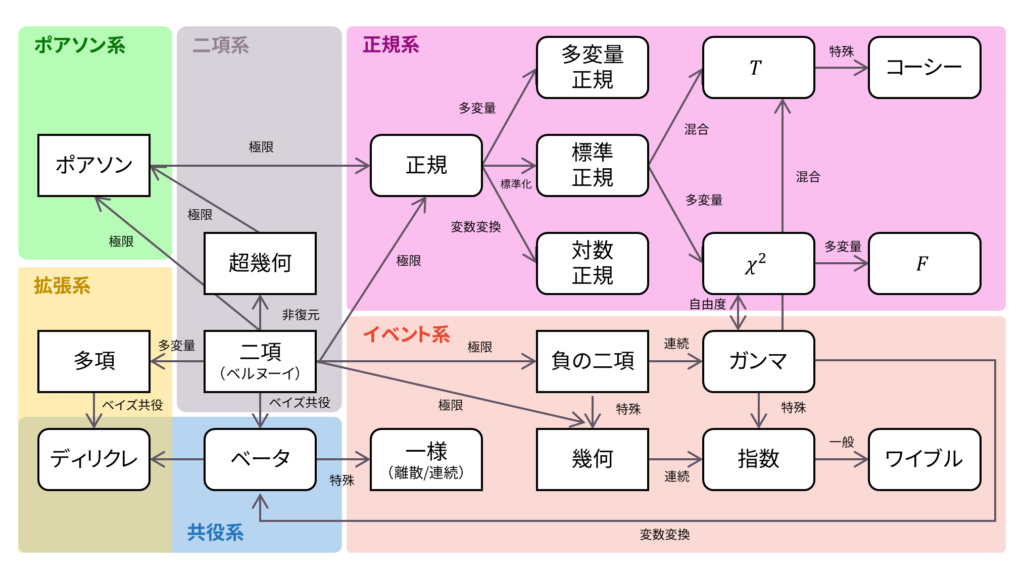
さて,もう少し具体的に中身をみていきましょう。上図はマクロな視点で見たときの箱に,それぞれどのような確率分布が格納されているのかを表しています。角が尖っている四角は離散型確率変数をとる分布,角が丸い四角は連続型確率変数をとる分布です。一様分布は離散型確率変数も連続型確率変数もとるため,少しいびつな四角になっています。矢印の添字は,どのようにして矢印の先の分布が導かれるのかを表しています。
「非復元」は続けて抽出する試行,「極限」は何らかの条件下である変数に対して極限を取るような操作,「多変量」は変数を拡張する操作,「ベイズ共役」は共役事前分布,「特殊」は矢印の先が矢印の元の分布の特殊なケースであること,「一般」は逆に矢印の先が矢印の元の分布の一般形であること,「混合」は複数の分布に従う確率変数を混合する操作,「変数変換」や「標準化」は変数を定義し直す操作,「連続」は変数を連続型確率変数とみなす操作,「自由度」はある特定のパラメータの違いであることを表しています。なお,上図は必ずしも全ての確率分布同士の関係性を網羅できているわけではないため,注意してください。
参考文献
本稿の執筆にあたり参考にした文献は,以下でリストアップしております。


コメント