本記事は「これなら分かる!はじめての数理統計学」シリーズに含まれます。
不適切な内容があれば,記事下のコメント欄またはお問い合わせフォームよりご連絡下さい。
離散一様分布
f_{X}(x) &= \frac{1}{n} \\[0.7em]
G_X(s) &=
\begin{cases}
\displaystyle\frac{s(1-s^{n})}{n(1-s)} & |s| < 1 \\
1 & s = 1
\end{cases} \\[0.7em]
E[X] &= \frac{n + 1}{2} \\[0.7em]
V[X] &= \frac{n^2-1}{12}
\end{align}
全ての事象の起こる確率が等しい分布を一様分布と呼びます。特に,確率変数が離散型の場合は離散一様分布と呼びます。離散一様分布に従う確率変数$X$に対し,実現値は
x \in \{1, \ldots, n\}
\end{align}
であり,確率母関数の変数は$|s|\leq1$とします。離散一様分布は再生性を持たず,ロードマップ中ではベータ分布の特殊な場合に相当します。
確率質量関数
離散一様分布は全ての事象の起こる確率が等しい分布ですので,確率質量関数は直感的に導かれます。
f_{X}(x) &= P(X=x) \\[0.7em]
&= \frac{1}{n}
\end{align}
ただし,$x=1,\cdots,n$とします。
確率母関数
確率母関数の定義に従って計算していきます。
G_{X}(s) &= E[s^{x}] \\[0.7em]
&= \sum_{x=1}^{n}P(X=x)\cdot s^{x} \\[0.7em]
&= \frac{1}{n} \sum_{x=1}^{n} s^{x}
\end{align}
ここで,高校数学の等比級数の公式を利用します。確率母関数の定義より$|s| \leq 1$であるため,まずは$|s| < 1$を考えます。
\frac{1}{n} \sum_{x=1}^{n} s^{x} &= \frac{1}{n}\cdot \frac{s(1-s^n)}{1-s} \\[0.7em]
&= \frac{s}{n} \frac{1-s^{n}}{1-s}
\end{align}
$s=1$のときは,以下のように計算されます。
\frac{1}{n} \sum_{x=1}^{n} s^{x} &= \frac{1}{n} \cdot n \\[0.7em]
&= 1
\end{align}
平均・分散
離散分布の平均と分散を求めるためには,確率母関数の性質を利用します。しかし,離散一様分布の場合は確率母関数を利用するとかえって煩雑な計算になってしまうため,平均・分散の定義に従って求めていきます。こちらも高校数学の和の公式や二乗和の公式を利用します。まずは,一次モーメント,すなわち期待値を求めましょう。
E[X] &= \sum_{x=1}^{n}\frac{1}{n}\cdot x \\[0.7em]
&= \frac{1}{n}\cdot\frac{1}{2}n(n+1) \\[0.7em]
&= \frac{n+1}{2}
\end{align}
次に,二次モーメントを求めましょう。
E[X^2] &= \sum_{x=1}^{n}\frac{1}{n}\cdot x^2 \\[0.7em]
&= \frac{1}{n}\cdot\frac{1}{6}n(n+1)(2n+1) \\[0.7em]
&= \frac{1}{6}(n+1)(2n+1)
\end{align}
したがって,分散は以下のように求められます。
V[X] &= E[X^2] - E[X]^2 \\[0.7em]
&= \frac{1}{6}(n+1)(2n+1) - \frac{(n+1)^2}{4} \\[0.7em]
&= \frac{n^2-1}{12}
\end{align}
再生性
再生性を示すためには,再生性を示したい分布に従う独立な二つの確率変数を考え,その和の確率母関数を計算したときに,パラメータが和の形になっていることを示します。
確率母関数の形からも推測される通り,離散一様分布は再生性を持ちません。実際に計算してみても,二つの確率変数の和の確率母関数のパラメータは和の形になっていませんので,再生性は持ちません。
G_{X+Y}(s) &= G_{X}(s) \cdot G_{Y}(s) \\[0.7em]
&= \frac{s}{m} \frac{1-s^{m}}{1-s} \cdot \frac{s}{n} \frac{1-s^{n}}{1-s} \\[0.7em]
&\neq \frac{s}{m + n} \frac{1-s^{m + n}}{1-s}
\end{align}
ロードマップ
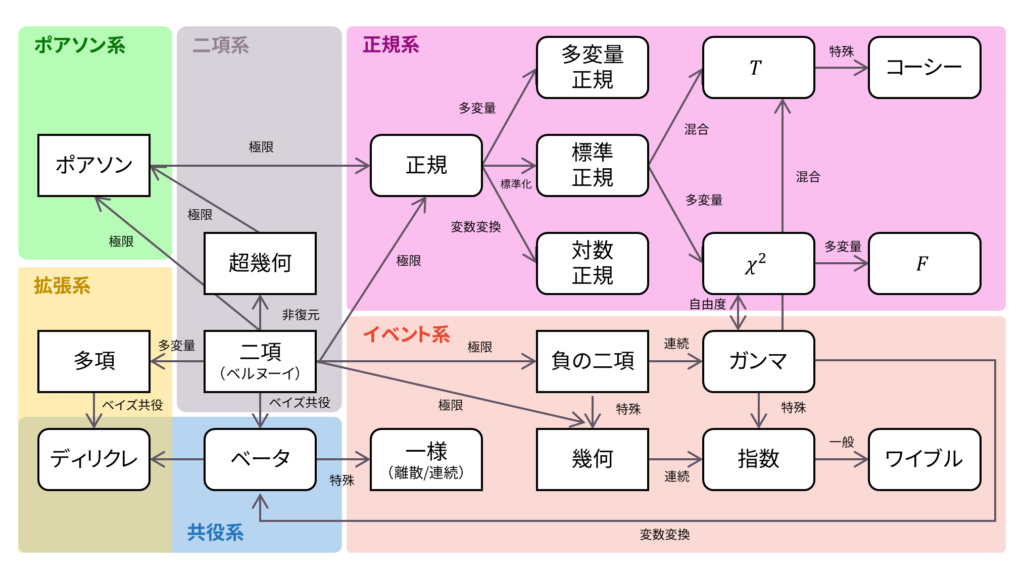
さて,ロードマップに戻りましょう。一様分布は,ロードマップの中での位置付けというのはさほど重要ではなく,情報を持たない確率分布としてベイズ統計で利用されています。以下の内容も参考になるでしょう。
情報を持たない確率分布は「情報を持たないという情報を持つ」確率分布と捉えることもできます。
参考文献
本稿の執筆にあたり参考にした文献は,以下でリストアップしております。


コメント