本記事は「これなら分かる!はじめての数理統計学」シリーズに含まれます。
不適切な内容があれば,記事下のコメント欄またはお問い合わせフォームよりご連絡下さい。
ラプラス分布
f_{X}(x) &= \frac{1}{2b} \exp\left( -\frac{|x-\mu|}{b} \right) \\[0.7em]
M_{X}(t) &= \frac{e^{\mu t}}{1-b^2 t^2} \\[0.7em]
E[X] &= \mu \\[0.7em]
V[X] &= 2b^2
\end{align}
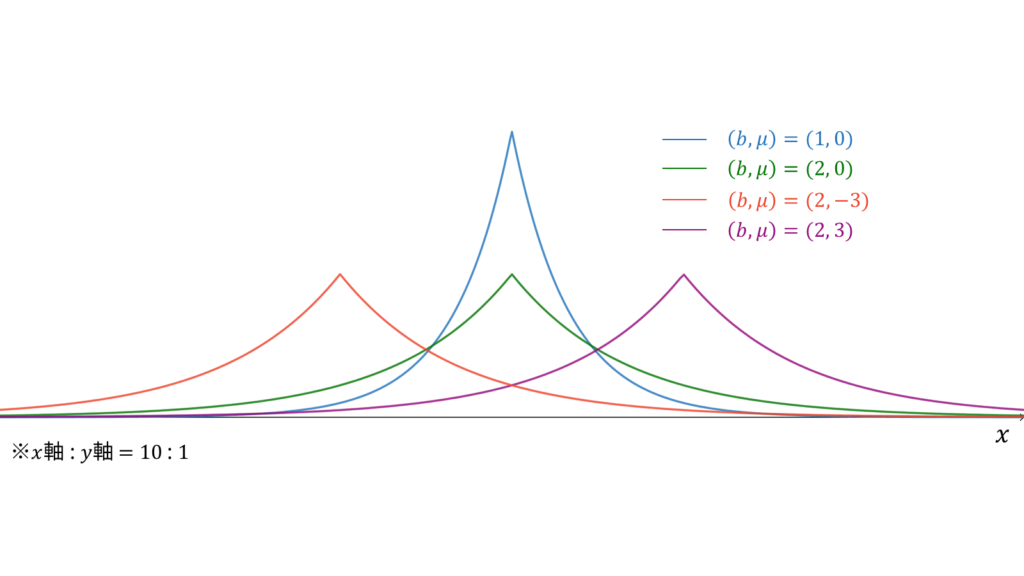
ラプラス分布は両側(二重)指数分布とも呼ばれ,指数分布を$y$軸に関して対称に貼り付けたような確率密度関数を持ちます。ラプラス分布に従う確率変数$X$に対し,実現値は
x \in \bbR
\end{align}
であり,モーメント母関数の変数は$|t| < 1/b$とします。概形は正規分布に似ていますが,頂点が正規分布よりも尖っています。
確率密度関数
定義より,ラプラス分布は指数分布を$y$軸に対して対称に貼り付けた分布ですので,以下の形になります。
f_{X}(x) &= C\cdot \exp\left( -\frac{|x-\mu|}{b} \right) \label{予想}
\end{align}
ただし,指数部は指数関数のように$\lambda$を用いるのではなく,正規分布のように平均$\mu$と尺度母数$b$を用いて表しました。指数部を正規分布と揃えて$|x-\mu|/\sigma^2$としないのは,$\sigma^2$が分散と一致しなくなってしまうからです。そのため,単に分布の形状を決定するパラメータという意味で「尺度母数」である$b$を持ち出しました。
さて,ラプラス分布($\ref{予想}$)は確率分布ですので,積分して$1$となるように$C$を定めましょう。
\frac{1}{C} &= \int_{-\infty}^{\infty} \exp\left( -\frac{|x-\mu|}{b} \right)dx \\[0.7em]
&= 2\int_{\mu}^{\infty} \exp\left( -\frac{x-\mu}{b} \right)dx \\[0.7em]
&= 2\left[ -b\exp\left( -\frac{x-\mu}{b} \right)\right]_{\mu}^{\infty} \\[0.7em]
&= 2b \label{C}
\end{align}
式($\ref{C}$)を式($\ref{予想}$)に代入すると,ラプラス分布の確率密度関数が得られます。
f_{X}(x) &= \frac{1}{2b} \exp\left( -\frac{|x-\mu|}{b} \right)
\end{align}
モーメント母関数
モーメント母関数の定義に従って計算していきます。
M_{X}(t) &= E[e^{tx}] \\[0.7em]
&= \int_{-\infty}^{\infty} e^{tx}\cdot \frac{1}{2b} \exp\left( -\frac{|x-\mu|}{b} \right) dx \label{置換前}
\end{align}
ここで,
y &= \frac{x-\mu}{b}
\end{align}
と置きます。すると,式($\ref{置換前}$)は以下のように変形できます。
M_{X}(t) &= \frac{1}{b}\int_{-\infty}^{\infty} e^{ t(by+\mu)-|y|} \cdot b\cdot dy \\[0.7em]
&= \frac{e^{\mu t}}{2}\int_{-\infty}^{\infty} e^{ tby-|y|} dy \\[0.7em]
&= \frac{e^{\mu t}}{2}\left\{\int_{-\infty}^{0} e^{(1+bt)y} dy+\int_{0}^{\infty} e^{-(1-bt)y} dy \right\}
\end{align}
第一項目の積分が収束するためには$1+bt > 0$が必要です。この条件下において,第一項目の積分は
\int_{-\infty}^{0} e^{(1+bt)y} dy &= \frac{1}{1+bt}\left[e^{(1+bt)y}\right]_{-\infty}^{0} \\[0.7em]
&= \frac{1}{1+bt}
\end{align}
と計算されます。同様に,第二項目の積分が収束するためには$1-bt > 0$が必要です。この条件下において,第二項目の積分は
\int_{0}^{\infty} e^{-(1-bt)y} dy &= -\frac{1}{1-bt}\left[e^{-(1-bt)y}\right]_{0}^{\infty} \\[0.7em]
&= \frac{1}{1-bt}
\end{align}
と計算されます。以上より,$1+bt > 0$かつ$1-bt > 0$のとき,すなわち
|t| < \frac{1}{b}
\end{align}
のとき,モーメント母関数$M_{Y}(t)$は以下のように求められます。
M_{X}(t) &= \frac{e^{\mu t}}{2}\left( \frac{1}{1+bt}+\frac{1}{1-bt}\right) \\[0.7em]
&= \frac{e^{\mu t}}{1-b^2t^2} \label{モーメント母関数}
\end{align}
平均・分散
連続分布の平均と分散を求めるためには,モーメント母関数の性質を利用します。まず,一次モーメント,すなわち期待値を求めます。
E[X] &= \left.M^{\prime}_{X}(t) \right|_{t=0} \\[0.7em]
&= \left. \frac{\mu e^{\mu t}(1-b^2t^2)+2b^2 te^{\mu t}}{(1-b^2t^2)^2} \right|_{t=0} \\[0.7em]
&= \left. \left\{\mu M_{X}(t) + 2M_{X}(t)\frac{b^2 t}{1-b^2t^2} \right\}\right|_{t=0} \\[0.7em]
&= \mu M_{X}(0) \\[0.7em]
&= \mu
\end{align}
ただし,式($\ref{モーメント母関数}$)より$M_{X}(0)=1$を利用しました。続いて,二次モーメントを求めます。
E[X^2] &= \left.M^{\prime\prime}_{X}(t) \right|_{t=0} \\[0.7em]
&= \left. \frac{d}{dx}\left\{\mu M_{X}(t) + 2M_{X}(t)\frac{b^2 t}{1-b^2t^2} \right\}\right|_{t=0} \\[0.7em]
&= \left.\left\{\mu M^{\prime}_{X}(t)+2M^{\prime}_{X}(t)\frac{b^2 t}{1-b^2t^2}+2M_{X}(t)\frac{b^2(1-b^2t^2)+2b^4t^2 }{(1-b^2t^2)^2}\right\}\right|_{t=0} \\[0.7em]
&= \mu M^{\prime}_{X}(0)+2M_{X}(0)b^2 \\[0.7em]
&= \mu E[X]+2b^2 \\[0.7em]
&= \mu^2+2b^2
\end{align}
最後に,一次モーメントと二次モーメントから分散を求めます。
V[X] &= E[X^2] - E[X]^2 \\[0.7em]
&= \mu^2+2b^2 - \mu^2\\[0.7em]
&= 2b^2
\end{align}
再生性
再生性を示すためには,再生性を示したい分布に従う独立な二つの確率変数を考え,その和のモーメント母関数を計算したときに,パラメータが和の形になっていることを示します。ラプラス分布のモーメント母関数の積をとっても同じモーメント母関数の形が現れないため,ラプラス分布に再生性はありません。
ロードマップ
さて,ロードマップに戻りましょう。ラプラス分布はロードマップに記載がないものの,指数分布を$y$軸に対して対称に貼り付けた分布として導入されました。モーメント母関数や平均・分散は平易な部分積分を用いて計算することができました。
参考文献
本稿の執筆にあたり参考にした文献は,以下でリストアップしております。


コメント