本記事は「これなら分かる!はじめての数理統計学」シリーズに含まれます。
不適切な内容があれば,記事下のコメント欄またはお問い合わせフォームよりご連絡下さい。
指数分布
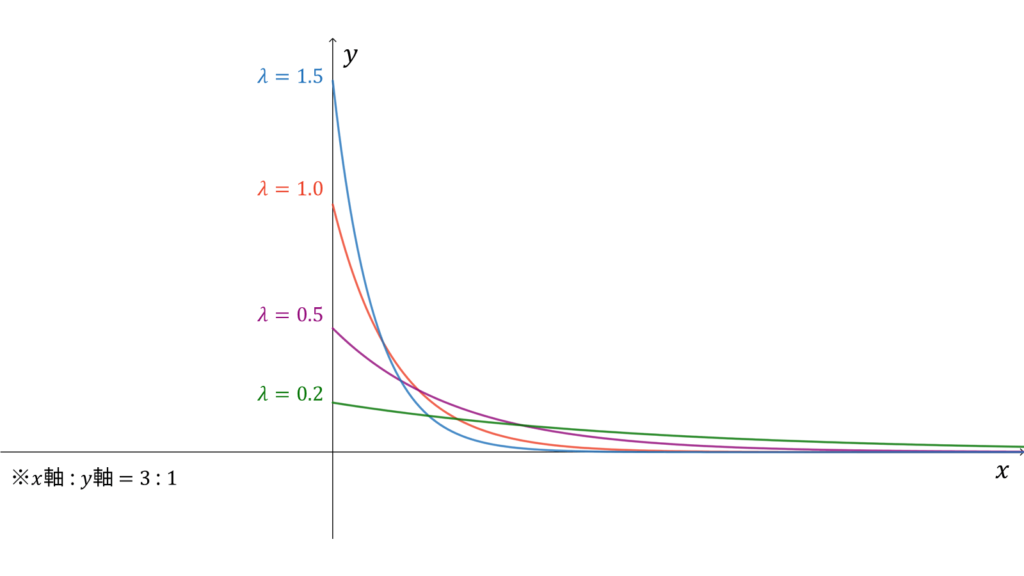
f_{X}(x) &= \lambda e^{-\lambda x} \\[0.7em]
M_{X}(t) &= \frac{1}{1-t/\lambda} \\[0.7em]
E[X] &= \frac{1}{\lambda} \\[0.7em]
V[X] &= \frac{1}{\lambda^2}
\end{align}
指数分布は事象の生起間隔の確率を与え,
\Exp (\lambda)
\end{align}
と表されます。ただし,$\lambda > 0$とします。指数分布に従う確率変数$X$に対し,実現値は
x \in \bbR_{+}
\end{align}
であり,モーメント母関数の変数は$t \in \bbR$とします。指数分布は再生性を持たず,ロードマップ中ではガンマ分布の特殊ケース$\Ga (1, \lambda)$に相当します。
確率密度関数
指数分布の確率密度関数の導出には,大きく分けて四つの方法があります。
- 幾何分布の連続拡張として導出
- 無記憶性の定義より導出
- 危険率が一定となる確率分布として導出
- ポアソン分布から導出
幾何分布の連続拡張として導出
時刻$t \in [0, \infty)$を長さ$1/n$の区間に分割して,各区間のインデックスを$k$とおきます。ポアソン分布の導出と同様に,各区間で事象$A$が起こる確率を,
p &= \frac{\lambda}{n}
\end{align}
で表し,$n \rightarrow \infty$を考えます。ただし,$\lambda > 0$とします。ここで,パラメータが$p$の幾何分布を考えると,インデックス$k$で初めて$A$が起こる確率は,
p\left(T=\frac{k}{n}\right) &= \left(1-p\right)^{k}\cdot p \\[0.7em]
&= \left(1-\frac{\lambda}{n}\right)^{k}\cdot \frac{\lambda}{n} \label{幾何分布}
\end{align}
となります。ただし,確率変数$T$は$A$が初めて起こる時刻を表し,$n,k,t$の定義から$t=k/n$となります。ここで,指数分布の確率密度関数を$f(t)$とおくと,確率密度関数の定義より$A$が微小区間$dt$の中で初めて起こる確率は以下のように表されます。
p(T\in dt) &= f(t)dt
\end{align}
$t=k/n$より$k=nt$となること,$n \rightarrow \infty$のとき区間$1/n$は微小量になることから$dt$と表されることに注意すると,式($\ref{幾何分布}$)の極限は以下のように計算できます。
f(t)dt &= \lim_{n\rightarrow \infty} p\left(T=\frac{k}{n}\right) \\[0.7em]
&=\lim_{n\rightarrow \infty} \left(1-\frac{\lambda}{n}\right)^{k} \frac{\lambda}{n} \\[0.7em]
&=\lim_{n\rightarrow \infty} \left(1-\frac{\lambda}{n}\right)^{nt}\lambda~dt \\[0.7em]
&=\lim_{n\rightarrow \infty} \lambda \left\{ \left(1-\frac{\lambda}{n}\right)^{-n/\lambda}\right\}^{-\lambda t} dt \\[0.7em]
&\rightarrow \lambda e^{-\lambda t} dt
\end{align}
ただし,ネイピア数$e$の定義を利用しました。以上より,指数分布の確率密度関数$f$は以下で表されることが分かりました。
f(t) &= \lambda e^{-\lambda t}
\end{align}
無記憶性の定義より導出
指数分布は,無記憶性を持つ連続型確率分布として導出されます。無記憶性の定義の左辺を条件付き確率の定義を用いて変形し,右辺を指数分布の累積密度関数$F$を用いて書き直すと,以下のようになります。
\frac{p\left(t \leq T<t+\Delta t,~T \geq t \right)}{p(T \geq t)} &= F(\Delta t) \label{無記憶性の定義}
\end{align}
ただし,上で述べた通り$q$が指数分布の累積密度関数そのものを表していることを利用しました。さて,左辺も$F$を用いて表すことで,式($\ref{無記憶性の定義}$)を$F$に関する方程式に仕上げましょう。まず,分母に関しては累積密度関数の余事象を用いて表すことができます。分子に関しても,累積密度関数の差で表すことができます。したがって,式($\ref{無記憶性の定義}$)は以下のように計算することができます。
\frac{F(t+\Delta t)-F(t)}{1-F(t)} &= F(\Delta t)
\end{align}
私たちの目標は,$F$を求めることでその導関数$f$を求めることです。左辺の分母が導関数の定義に似ていることに注目して,両辺を$\Delta t$で割ってみましょう。
\frac{F(t+\Delta t)-F(t)}{\Delta t}\cdot \frac{\Delta t}{1-F(t)} &= \frac{F(\Delta t)}{\Delta t} \\[0.7em]
&= \frac{F(0+\Delta t)-F(0)}{\Delta t} \label{極限前}
\end{align}
ただし,累積密度関数の定義より$F(0)=0$であることを用いました。続けて,式($\ref{極限前}$)の両辺で$\Delta \rightarrow 0$の極限を取りましょう。
\frac{f(t)}{1-F(t)} &= f(0) \label{極限後}
\end{align}
分かりやすさのため,$S(t)=1-F(t)$と置き,式($\ref{極限後}$)を微分方程式の形に書き直してみます。
\frac{-S^{\prime}(t)}{S(t)} &= -S^{\prime}(0) \label{微分方程式}
\end{align}
この微分方程式を,$F(0)=0$,$f(0)=\lambda$の初期条件で解きます。
初期条件の妥当性を確認しておきます。$F(0)=0$は,累積密度関数の定義より必ず成り立ちます。$f(0)=\lambda$は,危険率を用いて妥当性を確認することができますが,まとめて次のパートでお伝えすることにします。本パートでは,一旦微分方程式を解くための便宜上の仮定と理解しておいてください。
式($\ref{微分方程式}$)は変数分離形の微分方程式ですので,両辺を$t$で積分しましょう。
\log S(t) &= S^{\prime}(0)t + C
\end{align}
ただし,$C$は積分定数です。$S^{\prime}(0)=-f(0)$であることに注意すると,$S(t)$は以下のように表されます。
S(t) &= Ce^{-\lambda t}
\end{align}
ただし,定数はまとめて$C$と置きました。$S(t)=1-F(t)$と置きましたので,指数分布の累積密度関数および確率密度関数は以下で表されます。
F(t) &= 1-Ce^{-\lambda t} \\[0.7em]
f(t) &= F^{\prime}(t) \\[0.7em]
&= C \lambda e^{-\lambda t}
\end{align}
確率密度関数の定義より,以下が成り立ちます。
\int_{0}^{\infty} C\lambda e^{-\lambda t} &= 1
\end{align}
したがって,定数$C$は以下のように表されます。
C &=\left( \int_{0}^{\infty} \lambda e^{-\lambda t}\right)^{-1} \\[0.7em]
&= 1
\end{align}
以上より,指数分布の確率密度関数は以下のように表されることが分かりました。
f(t) &= \lambda e^{-\lambda t}
\end{align}
危険率が一定となる確率分布として導出
指数分布は,危険率が一定値$\lambda$となる確率分布として導入できます。危険率の定義より,以下が成り立ちます。
\lim_{\Delta \rightarrow 0} \frac{1}{\Delta} p(t \leq T < t+\Delta \mid T \geq t) &= \lambda
\end{align}
危険率の定義と無記憶性の定義が非常に似ていることに注意すると,先ほどまでの「無記憶性の定義より導出」のパートを流用できることが分かります。すなわち,式($\ref{極限前}$)の左辺が危険率における極限の対象を表していますので,式($\ref{極限後}$)より危険率は$f(0)$であることが分かります。
\lim_{\Delta \rightarrow 0} \frac{1}{\Delta} p(t \leq T < t+\Delta \mid T \geq t) &= \frac{f(t)}{1-F(t)} \\[0.7em]
&= f(0) \\[0.7em]
&= \lambda
\end{align}
危険率が一定値$\lambda$であるという仮定は,微分方程式の初期条件に$f(0)=\lambda$を与えることを意味していたのです。したがって,指数分布の確率密度関数の導出方法としては,無記憶性の定義に基づくものと危険率に基づくものは,本質的には同じ方針と捉えることができます。なお,ワイブル分布では危険率として定数以外を与えます。
ここからの計算は「無記憶性の定義より導出」と同様ですので割愛します。なお,危険率に基づく確率密度関数の導出に関する定理を用いれば,以下のように計算することも可能です。「無記憶性の定義より導出」と本質的な操作に変わりはありません。
f(t) &= -\frac{d}{dt} \exp\left\{-\int_{0}^{t}l(u)du \right\} \\[0.7em]
&= -\frac{d}{dt} \exp\left\{-\int_{0}^{t}\lambda du \right\} \\[0.7em]
&= -\frac{d}{dt} e^{-\lambda t} \\[0.7em]
&= \lambda e^{-\lambda t}
\end{align}
ポアソン分布から導出
ある一定時間における事象の起こる回数を$X$,事象の起こる回数の期待値を$\tau$とすれば,ポアソン分布の確率質量関数$g(x)$は以下のように表されます。
g(x) &= \frac{\tau^x}{x!} e^{-\tau} \label{ポアソン分布}
\end{align}
ここで,ある一定時間として$(0, t]$を考えます。単位時間における事象の起こる回数の期待値を$\lambda$とおけば,
\tau &= \lambda t
\end{align}
となりますので,先ほどのポアソン分布の確率質量関数($\ref{ポアソン分布}$)に代入します。
g(x) &= \frac{(\lambda t)^x}{x!}e^{-\lambda t}
\end{align}
ここで,事象が初めて起こるまでの待ち時間を表す確率変数$T$を導入します。すると,事象の起こる回数$X$を使って,時間$t$まで事象$X$が$1$回も起こっていない確率$p(T > t)$を記述することができます。
p(T > t) &= f(x=0) \\[0.7em]
&= e^{-\lambda t}
\end{align}
事象が起こるのは少なくとも時間$t$よりも長い時間待った後になることから,時間$t$まで事象が$1$回も起こらない確率が$p(T>t)$となります。
$p(T>t)$の余事象は
p(T \leq t) &= 1 - p(T > t) \\[0.7em]
&= 1 - e^{-\lambda t}
\end{align}
と表され,$1$回しか起こらない事象が初めて起こるために要する時間$t$の累積分布関数となります。したがって,事象が初めて起こるまでの待ち時間,すなわち指数分布の確率密度関数$f(t)$は以下のように求められます。
f(t) &= \frac{d}{dt} (1 - e^{-\lambda t}) \\[0.7em]
&= \lambda e^{-\lambda t}
\end{align}
モーメント母関数
モーメント母関数の定義に従って計算していきます。
M_{X}(t) &= E[e^{tx}] \\[0.7em]
&= \int_0^{\infty} e^{tx} \lambda e^{-\lambda x}dx \\[0.7em]
&= \int_0^{\infty} \lambda e^{(t -\lambda) x}dx \label{モーメント母関数}
\end{align}
式($\ref{モーメント母関数}$)の収束条件は$t-\lambda < 0$ですので,$t-\lambda \geq 0$の場合は指数分布のモーメント母関数は存在しません。しかし,モーメント母関数の定義より,$t$は$0$に限りなく近いものとしてOKですので,以下は$t-\lambda < 0$としてモーメント母関数の計算を進めていきます。
M_{D}(t) &= \left[\frac{\lambda}{t-\lambda} e^{(t-\lambda)x} \right]_0^{\infty} \\[0.7em]
&= \left( 1-\frac{t}{\lambda} \right)^{-1}
\end{align}
平均・分散
連続分布の平均と分散を求めるためには,モーメント母関数の性質を利用します。まず,一次モーメント,すなわち期待値を求めます。
E[X] &= \left.M^{\prime}_{X}(t) \right|_{t=0} \\[0.7em]
&= \left. \frac{1}{\lambda} \left( 1 - \frac{t}{\lambda} \right)^{-2} \right|_{t=0} \\[0.7em]
&= \frac{1}{\lambda}
\end{align}
続いて,二次モーメントを求めます。
E[X^2] &= \left.M^{\prime\prime}_{X}(t) \right|_{t=0} \\[0.7em]
&= \left. \frac{2}{\lambda^2} \left( 1 - \frac{t}{\lambda} \right)^{-3} \right|_{t=0} \\[0.7em]
&= \frac{2}{\lambda^2}
\end{align}
最後に,一次モーメントと二次モーメントから分散を求めます。
V[X] &= E[X^2] - E[X]^2 \\[0.7em]
&= \frac{2}{\lambda^2} - \frac{1}{\lambda^2}\\[0.7em]
&= \frac{1}{\lambda^2}
\end{align}
再生性
再生性を示すためには,再生性を示したい分布に従う独立な二つの確率変数を考え,その和のモーメント母関数を計算したときに,パラメータが和の形になっていることを示します。指数分布のモーメント母関数の積をとっても同じモーメント母関数の形が現れないため,指数分布に再生性はありません。
ロードマップ
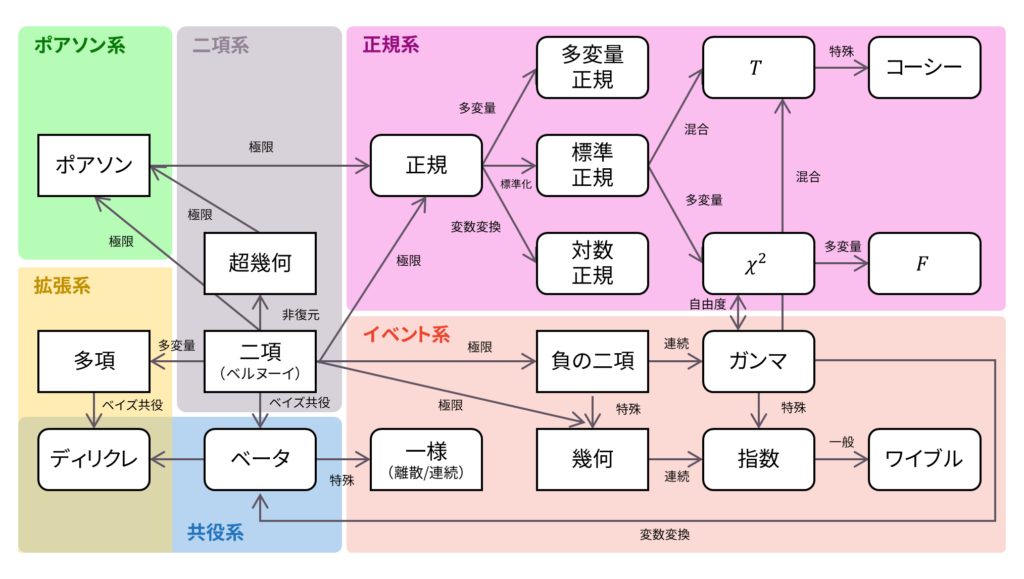
さて,ロードマップに戻りましょう。 指数分布は以下の四つの方針で導入されました。
- 幾何分布の連続拡張として導出
- 無記憶性の定義より導出
- 危険率が一定となる確率分布として導出
- ポアソン分布から導出
以下の内容も参考になるでしょう。
参考文献
本稿の執筆にあたり参考にした文献は,以下でリストアップしております。


コメント
コメント一覧 (6件)
すいません、今統計学の勉強をしているものです。
幾何分布の連続拡張として導出からの(14)から(15)にかけての証明で
"ネイピア数の定義を利用しました"というところがよくわかりません。。
{(1-λ/n)}^-n/λの式がネイピア数eになるのでしょうか。。
sunaga様
ご質問ありがとうございます。ネイピア数の定義
\begin{align}
e &= \lim_{x\rarr 0}(1+x)^{1/x}
\end{align}
で$x=-\lambda/n$を適用しています。
コメントありがとうございます。
あと、追記ですいません、(12)のλ/n が(13)では、nがなくなりλだけになっているのはどういうことでしょうか。。
本文にある「$n \rightarrow \infty$のとき区間$1/n$は微小量になることから$dt$と表されることに注意すると」の通りです。
あ、dt=1/nになったんですね。わかりました!
あと最後ですが、(14)の式にある累乗 (-λ/n) と{ }にある-λt ですが、-
累乗同士を掛けるとn/λ・-λt = ntになる。
nt を -( )^-n/λ・{ }^ -λt にわけたと考えてよかったですか?
はい。合ってます。定番の式変形なので必ずおさえてください。