本記事は「これなら分かる!はじめての数理統計学」シリーズに含まれます。
不適切な内容があれば,記事下のコメント欄またはお問い合わせフォームよりご連絡下さい。
標準コーシー分布
f_{X}(x) &= \frac{1}{\pi}\frac{1}{x^2 + 1} \\[0.7em]
\phi_X(t) &= e^{-|t|}
\end{align}
連続一様分布に従う確率変数
Y \sim U(-\pi/2, \pi/2)
\end{align}
に対して,以下の変数変換
X &= \tan Y
\end{align}
を考えたとき,$X$が従う分布を標準コーシー分布と呼びます。標準コーシー分布に従う確率変数$X$に対し,実現値は
x \in \bbR
\end{align}
であり,期待値・分散・モーメント母関数が定義されません。ただし,特性関数は存在します。標準コーシー分布は再生性を持たず,ロードマップ中では$T$分布の特殊な場合(自由度$1$)に相当します。ただし, 独立に標準コーシー分布に従う確率変数の算術平均に関しては再生性を持ちます。なお,標準コーシー分布は正規分布よりも裾が重い分布として有名です。
標準コーシー分布を単にコーシー分布と呼ぶ場合もあります。一般には,コーシー分布は位置母数と尺度母数を用いて定義されますが,標準コーシー分布が最もよく利用されることから表記が簡略化されたものと推測されます。本稿でも,以下では標準コーシー分布のことを「コーシー分布」と表記します。
確率密度関数
コーシー分布は$T$分布の特殊な場合ではありますが,確率密度関数を導出する際は異なるアプローチをとります。実は,連続一様分布$U(-\pi/2, \pi/2)$に従う確率変数$X$に対して,以下の変数変換
X &= \tan Y
\end{align}
を考えたとき,$X$が従う分布がコーシー分布になります。実際に確率密度変数を導出しましょう。逆変換$y=\arctan x$のヤコビアンは
\frac{dy}{dx} &= \frac{1}{x^2+1}
\end{align}
になるので,$x\in \mathbb{R}$において,コーシー分布の確率密度関数$f(x)$は以下のようになります。
f(x) &= \frac{1}{\pi}\frac{1}{x^2+1}
\end{align}
モーメント母関数・平均・分散
通常,モーメント母関数を求めるときはモーメント母関数の定義に従って計算していきます。しかし,実数領域ではコーシー分布の原点周りの一次モーメント,すなわち平均は定義されないため,モーメント母関数も定義されません。そこで,以下ではコーシー分布の期待値が存在しないことを示してみましょう。定義より,コーシー分布の平均は
E[X] &= \int_{-\infty}^{\infty} \frac{1}{\pi}\frac{x}{x^2+1} dx \\[0.7em]
&= \frac{1}{\pi}\left\{ \lim_{b\rightarrow\infty}\frac{1}{2}\log(1+b^2) - \lim_{a\rightarrow-\infty}\frac{1}{2}\log(1+a^2) \right\}
\end{align}
と表されます。期待値を計算すると広義積分が登場するため,期待値は定義されないのです。それゆえ,分散も存在しません。
ちなみに,大数の法則は期待値の存在を仮定しているために,コーシー分布では大数の法則が成り立ちません。同様に,中心極限定理も成り立ちません。実際,コーシー分布は外れ値をとる確率が高い分布として知られていて,この性質を「裾が重い」と呼びます。そのため,いくらサンプル数を増やしたからといって,期待値は特定の値に収束することはないのです。
再生性
再生性を示すためには,再生性を示したい分布に従う独立な二つの確率変数を考え,その和のモーメント母関数を計算したときに,パラメータが和の形になっていることを示します。コーシー分布は,算術平均に関して再生性を持ちます。証明には複素積分を必要とするため,付録にて証明を行っています。
コーシー分布は算術平均に関して再生性を持つため,ここでも中心極限定理が適用されないことが分かります。
ロードマップ
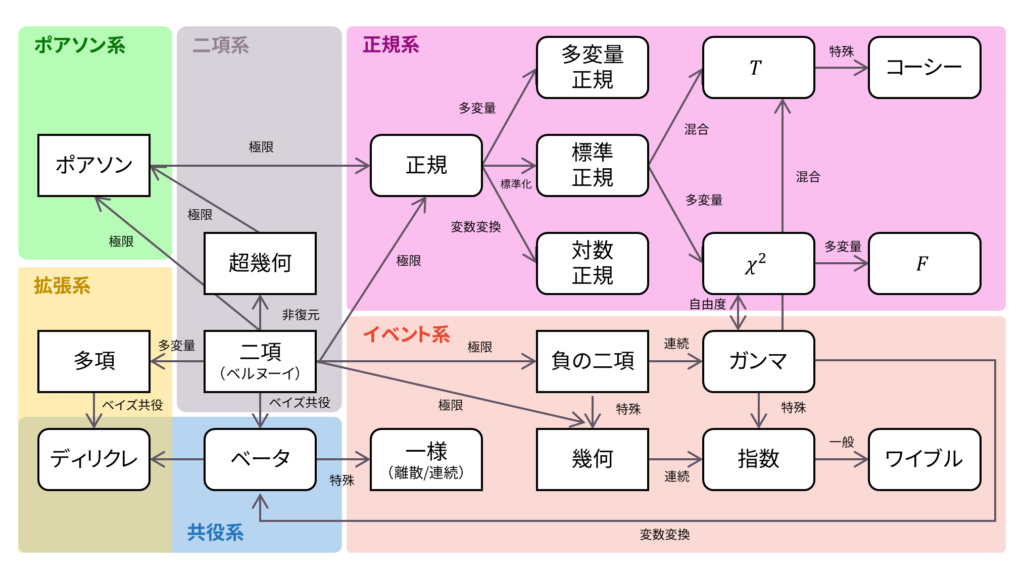
さて,ロードマップに戻りましょう。 コーシー分布は,一様分布に従う確率変数に対して変数変換を施すことで導出しました。以下の内容も参考になるでしょう。
参考文献
本稿の執筆にあたり参考にした文献は,以下でリストアップしております。


コメント