本記事は「これなら分かる!はじめての数理統計学」シリーズに含まれます。
不適切な内容があれば,記事下のコメント欄またはお問い合わせフォームよりご連絡下さい。
t分布
f_{X}(x) &= \frac{1}{\sqrt{n}B(n/2, 1/2)}\left( 1+\frac{x^2}{n} \right)^{-(n+1)/2} \\[0.7em]
E[X] &= 0 && (n > 1)\\[0.7em]
V[X] &= \frac{n}{n-2}&&(n > 2)
\end{alignat}
ただし,平均は$n>1$のときに限り存在し,分散は$n>2$のときに限り存在する。また,$B(\cdot)$はベータ関数を表す。
B(a, b) &= \int_0^1 x^{a-1}(1-x)^{b-1}dx
\end{align}
以下で定義される独立な確率変数
Z &\sim N(0,1) \\[0.7em]
W &\sim \chi^2(n)
\end{align}
に対し,確率変数
X &= \frac{Z}{\sqrt{W/n}}
\end{align}
が従う分布を自由度$n$のt分布と呼び,
t(n)
\end{align}
と表します。t分布に従う確率変数$X$に対し,実現値は
x \in \bbR
\end{align}
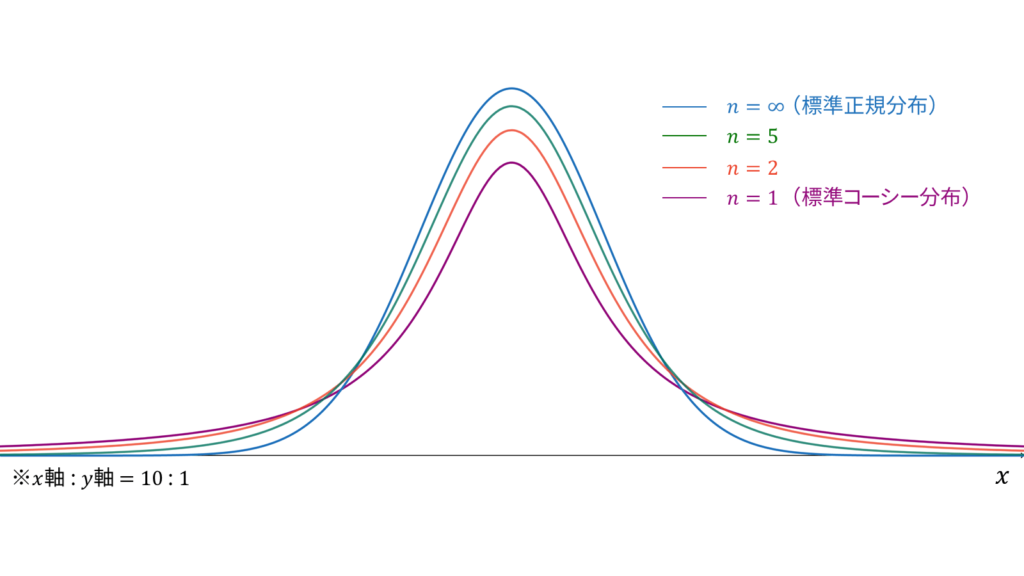
であり,モーメント母関数は存在しません。t分布は再生性を持たず,ロードマップ中では標準正規分布とカイ二乗分布の混合分布に相当します。
t分布はイギリスの統計学者ウィリアム・ゴセットによって発見されました。ゴセットは分散の推定値に標本分散を用いることの不当性に気付いたことをきっかけに,t分布を発見したと言われています。彼はアイルランドにあるビール会社ギネスの社員として働いており,秘密保持の観点から本名で論文を発表することができませんでした。そこで,彼はstudentという仮名で論文を発表したため,スチューデントのt分布と呼ばれることもあります。
確率密度関数
t分布の確率密度関数の導出には,大きく分けて二つの方法があります。
- 標準正規分布とカイ二乗分布に従う二つの確率変数の変数変換
- 正規分布とガンマ分布の混合
標準正規分布とカイ二乗分布に従う二つの確率変数の変換
先ほど導入した確率変数$X$が従う分布の確率密度関数を求めましょう。$Y=W$とおくと,逆変換は以下のようになります。
z &= x\sqrt{\frac{y}{n}} \\[0.7em]
w &= y
\end{align}
標準正規分布とカイ二乗分布の確率密度関数より,同時分布$g(z, w)$は以下のようになります。
g(z, w) &= \frac{1}{\sqrt{2\pi}} e^{-z^2/2}\frac{w^{n/2-1}e^{-w/2}}{2^{n/2}\Gamma(n/2)}
\end{align}
また,ヤコビアンは以下のように計算できます。
J
&= \abs\left(\left|
\begin{array}{cc}
\partial z/ \partial x & \partial z/\partial y \\[0.7em]
\partial w/ \partial x & \partial w/\partial y \\[0.7em]
\end{array}
\right|\right)\\[0.7em]
&= \abs\left(\left|
\begin{array}{cc}
\sqrt{y/n} & x/(2\sqrt{ny}) \\[0.7em]
0 & 1 \\[0.7em]
\end{array}
\right|\right)\\[0.7em]
&= \sqrt{\frac{y}{n}}
\end{align}
確率変数の変数変換に関する定理より,同時分布$f(x, y)$は以下のように求められます。
f(x, y) &= \frac{1}{\sqrt{2\pi}} e^{-x^2y/(2n)}\frac{y^{n/2-1}e^{-y/2}}{2^{n/2}\Gamma(n/2)}\sqrt{\frac{y}{n}} \label{同時}
\end{align}
我々が求めたいのは$X$が従う分布の確率密度関数ですので,式($\ref{同時}$)を$Y$に関して周辺化してあげます。$Y=W$の定義より定義域が$[0, \infty)$となることに注意して下さい。
f(x) &= \int_{0}^{\infty} f(x, y) dy \\[0.7em]
&= \int_{0}^{\infty} \frac{1}{\sqrt{2\pi}} e^{-x^2y/(2n)}\frac{y^{n/2-1}e^{-y/2}}{2^{n/2}\Gamma(n/2)}\sqrt{\frac{y}{n}} dy \\[0.7em]
&= \frac{1}{\sqrt{2\pi n}}\frac{1}{2^{n/2}\Gamma(n/2)}\int_{0}^{\infty} y^{(n+1)/2-1}e^{-y(1+x^2/n)/2} dy
\end{align}
ここで,
2^{-1}\left(1+\frac{x^2}{n}\right)y &= my \label{m}\\[0.7em]
&= s
\end{align}
と置きます。このとき,
dy &= m^{-1}ds
\end{align}
が成り立つことに注意すると,
f(x) &= \frac{1}{\sqrt{2\pi n}}\frac{1}{2^{n/2}\Gamma(n/2)}\int_{0}^{\infty} (m^{-1}s)^{(n+1)/2-1}e^{-s} m^{-1}ds \\[0.7em]
&= \frac{1}{\sqrt{2\pi n}}\frac{1}{2^{n/2}\Gamma(n/2)}m^{-(n+1)/2}\int_{0}^{\infty} s^{(n+1)/2-1}e^{-s} ds \label{1}\\[0.7em]
&= \frac{1}{\sqrt{2\pi n}}\frac{m^{-(n+1)/2}}{2^{n/2}\Gamma(n/2)}\Gamma\left(\frac{n+1}{2}\right) \label{2}\\[0.7em]
&= \frac{1}{\sqrt{2\pi n}}\frac{2^{(n+1)/2}}{2^{n/2}\Gamma(n/2)}\left(1+\frac{x^2}{n}\right)^{-(n+1)/2}\Gamma\left(\frac{n+1}{2}\right) \label{3}\\[0.7em]
&= \frac{1}{\sqrt{n}}\frac{\Gamma\left(n/2+1/2\right)}{\Gamma(n/2)\Gamma(1/2)}\left(1+\frac{x^2}{n}\right)^{-(n+1)/2} \label{4}\\[0.7em]
&= \frac{1}{\sqrt{n}B(n/2, 1/2)}\left( 1+\frac{x^2}{n} \right)^{-(n+1)/2}\label{t分布}
\end{align}
と計算できます。ただし,式($\ref{1}$)から式($\ref{2}$)はガンマ関数の定義,式($\ref{2}$)から式($\ref{3}$)は$m$の定義($\ref{m}$),式($\ref{3}$)から式($\ref{4}$)は$2^{(n+1)/2}$の約分,式($\ref{4}$)から式($\ref{t分布}$)はベータ関数とガンマ関数の関係を利用しました。
正規分布とガンマ分布の混合
t分布は正規分布$\N (0, 1/\theta)$を$\theta$についてガンマ分布$\Ga (m, \lambda)$で混合することでも得られます。ただし,$m$は先ほど定めた$m$とは異なり,新しくガンマ分布のパラメータとして導入しています。分布の混合を考えるときは,以下の設定を考えたときに同時分布の周辺分布を計算します。
X|\theta &\sim \N (0, 1/\theta) \\[0.7em]
\theta &\sim \Ga (m, \lambda)
\end{align}
実際に計算を進めてみます。
f(x) &= \int_{0}^{\infty} p(x|\theta)\cdot p(\theta)d\theta \\[0.7em]
&= \int_{0}^{\infty} \sqrt{\frac{\theta}{2\pi}}e^{-\theta x^2/2}\cdot \frac{\lambda^m}{\Gamma(m)}\theta^{m-1}e^{-\lambda \theta}d\theta \\[0.7em]
&= \frac{\lambda^m}{\sqrt{2\pi}~\Gamma(m)}\int_{0}^{\infty} \theta^{(m+1/2)-1}e^{-(\lambda+x^2/2) \theta} d\theta
\end{align}
先ほどと同様に,
\left(\lambda + \frac{x^2}{2}\right)\theta &= \omega \theta \\[0.7em]
&= \phi
\end{align}
と置きます。このとき,
d\theta &= \omega^{-1}d\phi
\end{align}
が成り立つことに注意すると,
f(x) &= \frac{\lambda^m}{\sqrt{2\pi}~\Gamma(m)}\int_{0}^{\infty} (\omega^{-1} \phi)^{(m+1/2)-1}e^{-\phi} \omega^{-1}d\phi \\[0.7em]
&= \frac{\lambda^m}{\sqrt{2\pi}~\Gamma(m)} \omega^{-(m+1/2)} \Gamma\left( m+\frac{1}{2} \right) \\[0.7em]
&= \frac{\lambda^m}{\sqrt{2\pi}~\Gamma(m)} \left(\lambda + \frac{x^2}{2}\right)^{-(m+1/2)} \Gamma\left( m+\frac{1}{2} \right) \\[0.7em]
&= \frac{\lambda^m}{\sqrt{2\pi}~\Gamma(m)} \left\{\lambda\left(1 + \frac{x^2}{2\lambda}\right)\right\}^{-(m+1/2)} \Gamma\left( n+\frac{1}{2} \right) \\[0.7em]
&= \frac{\Gamma(m+1/2)}{\sqrt{2\pi}\lambda^{1/2}~\Gamma(m)}\left(1 + \frac{x^2}{2\lambda}\right)^{-(m+1/2)}\\[0.7em]
&= \frac{\Gamma(m+1/2)}{\sqrt{2\lambda}~\Gamma(m)\Gamma(1/2)}\left(1 + \frac{x^2}{2\lambda}\right)^{-(m+1/2)}\\[0.7em]
&= \frac{1}{\sqrt{2\lambda}B(m, 1/2)}\left(1 + \frac{x^2}{2\lambda}\right)^{-(m+1/2)}
\end{align}
と計算できます。ここで,$m=\lambda=n/2$と置くと,
f(x) &= \frac{1}{\sqrt{n}B(n/2, 1/2)}\left( 1+\frac{x^2}{n} \right)^{-(n+1)/2}
\end{align}
となり,t分布の確率密度関数と一致します。
モーメント母関数
t分布のモーメント母関数は存在しません。
平均・分散
連続分布の平均と分散を求めるためには,モーメント母関数の性質を利用します。しかし,t分布にはモーメント母関数が存在しないため,少し工夫して平均と分散の導出を行いましょう。t分布の原点周りの一次モーメント,すなわち平均は被積分関数が奇関数であることに注目すれば,定義より簡単に求めることができます。
E[X] &= \int_{-\infty}^{\infty}x\cdot \frac{1}{\sqrt{n}B(n/2, 1/2)}\left( 1+\frac{x^2}{n} \right)^{-(n+1)/2} dx \\[0.7em]
&= C\int_{-\infty}^{\infty}h(x) dx \label{奇関数}
\end{align}
ただし,
h(x) &= x\left( 1+\frac{x^2}{n} \right)^{-(n+1)/2} \\[0.7em]
C &= \frac{1}{\sqrt{n}B(n/2, 1/2)}
\end{align}
と置きました。$h(-x)=-h(x)$となるため,$h(x)$は奇関数となります。したがって,被積分関数$h(x)$が収束するときに限り,積分($\ref{奇関数}$)は$0$となります。そこで,まずは$h(x)$の広義積分が収束する条件を考えましょう。
多くの書籍やWeb上の資料では,$h(x)$の収束性に関する議論がなされていないために,自由度に関わらずt分布の平均が存在することになっています。コーシー分布がt分布の特殊な場合であり,コーシー分布では平均が定義されないことを踏まえると,t分布でも平均が存在しない自由度がありますので十分に注意して下さい。
対称性より,$h(x)$の広義積分のうち定義域が正の部分のみを考えましょう。
\int_{-\infty}^{\infty}h(x) dx &= -\frac{n}{n+1} \lim_{a\rightarrow \infty}\left[\left( 1+\frac{x^2}{n} \right)^{-(n+1)/2}\right]_{0}^{a} \\[0.7em]
&= -\frac{n}{n+1} \left\{\lim_{a\rightarrow \infty}\left( 1+\frac{a^2}{n} \right)^{-(n+1)/2}-1\right\} \label{広義積分}
\end{align}
式($\ref{広義積分}$)における被極限関数の指数部分が$-1$より小さい,すなわち$1<n$のときに広義積分($\ref{広義積分}$)が存在することが分かります。以上より,t分布の自由度が$1<n$のときに原点周りの一次モーメント,すなわち平均が$0$となることが示せました。
続いて,原点周りの二次モーメントを求めます。多くの資料では,原点周りの一次モーメントと同様に定義に基づいて計算していますが,被積分関数が奇関数とならないため計算がやや複雑になってしまうという欠点があります。そこで,本稿ではt分布が複数の確率変数を組み合わせた変数変換により定義されている点に着目し,二次モーメントをベータ関数を用いて簡単に計算する方法をお伝えします。まず,t分布の確率密度関数($\ref{t分布}$)の形に着目し,以下の新しい確率変数を導入します。
U &= \left(1+\frac{X^2}{n}\right)^{-1} \label{U}
\end{align}
t分布とベータ分布の関係性で説明している通り,
U &\sim \Be(n/2,1/2)
\end{align}
となります。式($\ref{U}$)を変形すると,
X^2 &= nU^{-1}-n
\end{align}
となりますので,期待値の線形性に注意すると,原点周りの二次モーメントは以下のように計算されます。
E\left[ X^2\right] &= nE\left[U^{-1}\right]-n \label{二次モーメント}
\end{align}
ここで,$E[U^{-1}]$を定義から計算します。
E\left[U^{-1}\right] &= \frac{1}{B(n/2,~1/2)}\int_{0}^{1}\frac{1}{u}\cdot u^{n/2-1}(1-u)^{1/2-1}du \\[0.7em]
&= \frac{1}{B(n/2,~1/2)}\int_{0}^{1}u^{(n/2-1)-1}(1-u)^{1/2-1}du \\[0.7em]
&= \frac{1}{B(n/2,~1/2)}\cdot B(n/2-1,~1/2) \label{5}\\[0.7em]
&= \frac{\Gamma(n/2+1/2)}{\Gamma(n/2)\Gamma(1/2)}\cdot \frac{\Gamma(n/2-1)\Gamma(1/2)}{\Gamma(n/2-1/2)} \label{6}\\[0.7em]
&= \frac{n/2-1/2}{n/2-1} \label{7}\\[0.7em]
&= \frac{n-1}{n-2} \label{逆数}
\end{align}
ただし,式($\ref{5}$)から式($\ref{6}$)はベータ関数とガンマ関数の関係を利用し,式($\ref{6}$)から式($\ref{7}$)ではガンマ関数と階乗の関係を利用しました。また,ガンマ関数と階乗の関係を利用するため,$n>2$としました。
せっかく変数変換を用いて原点周りの二次モーメントを求める方針を採用したのに,定義から計算するフェーズが残されているのかと感じた方もおられるでしょう。しかし,上で計算した通り,ベータ関数に従う確率変数の逆数の期待値はベータ関数とガンマ関数の性質より非常に簡単に求めることができます。これは,ガンマ関数の階乗としての性質を利用することでうまく約分できることに起因しています。
式($\ref{逆数}$)を式($\ref{二次モーメント}$)に代入すると,
E\left[X^2\right] &= \frac{n}{n-2}
\end{align}
が得られます。したがって,t分布の分散が$n>2$において以下のように求められることが分かりました。
V[X] &= E\left[X^2\right]-E[X]^2 \\[0.7em]
&= \frac{n}{n-2}
\end{align}
再生性
再生性を示すためには,再生性を示したい分布に従う独立な二つの確率変数を考え,その和のモーメント母関数を計算したときに,パラメータが和の形になっていることを示します。t分布のモーメント母関数は存在せず,特性関数も複雑な形をしており積をとっても同じ関数の形が現れないため,t分布に再生性はありません。
ロードマップ
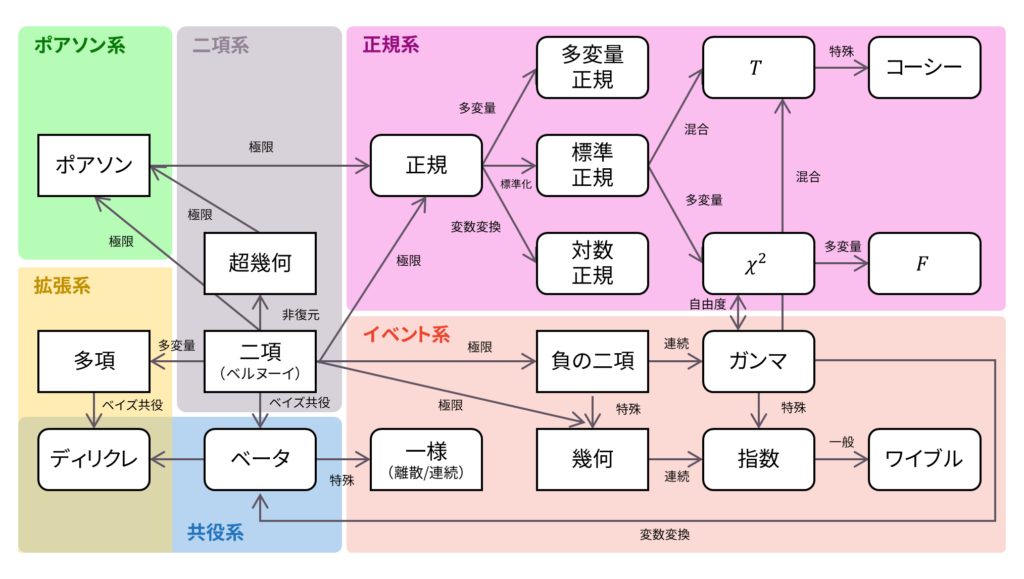
さて,ロードマップに戻りましょう。t分布は標準正規分布とカイ二乗分布に従う二つの確率変数の変数変換を用いて導出されるほか,正規分布とガンマ分布の混合によっても導出されました。以下の内容も参考になるでしょう。コーシー分布がt分布の特殊な場合であることは,別ページにて示します。
参考文献
本稿の執筆にあたり参考にした文献は,以下でリストアップしております。


コメント