本記事は「これなら分かる!はじめての数理統計学」シリーズに含まれます。
不適切な内容があれば,記事下のコメント欄またはお問い合わせフォームよりご連絡下さい。
ベータ分布
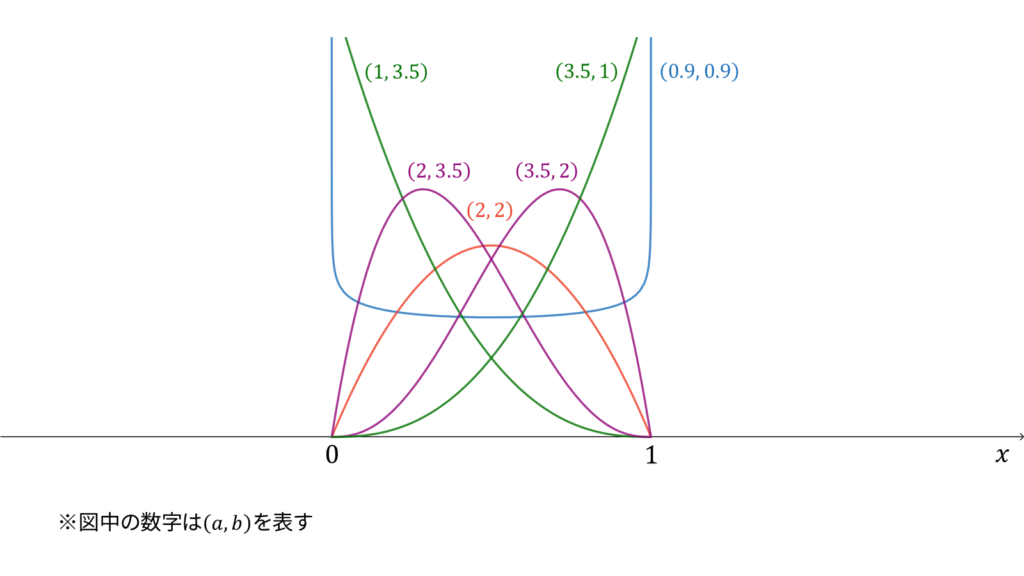
f_{X}(x) &= \frac{1}{B(a, b)}x^{a-1}(1-x)^{b-1} \\[0.7em]
E[X] &= \frac{a}{a+b} \\[0.7em]
V[X] &= \frac{ab}{(a+b)^2(a+b+1)}
\end{align}
ただし,$B(\cdot)$はベータ関数を表す。
B(a, b) &= \int_0^1 x^{a-1}(1-x)^{b-1}dx
\end{align}
ベータ分布は二項分布の共役事前分布として導入され,
\Be (a, b)
\end{align}
と表します。ベータ分布に従う確率変数$X$に対し,実現値は
x \in [0, 1]
\end{align}
であり,モーメント母関数の変数は$t \in \bbR$とします。ベータ分布は再生性を持たず,ロードマップ中では二項分布のベイズ共役に相当しています。ベータ分布は,ガンマ分布に従う確率変数の変数変換を利用しても導くことができます。なお,ベータ分布のモーメント母関数は存在しますが,利用されることが少ないためここでは割愛することにします。
確率密度関数
ベータ分布の確率密度関数の導出方法には,大きく分けて二つあります。
- 二項分布の共役事前分布として導入
- ガンマ分布に従う確率変数の変数変換を利用
二項分布の共役事前分布として導出
ベータ分布は,二項分布の共役事前分布として導入されます。共役事前分布というのは,尤度関数との積を計算したときに事後分布と形が同じになるような事前分布のことを指します。この場合,尤度関数である二項分布にかけ合わせることで同じ形が出現するような分布であることを意味しています。
(\text{ベータ分布}) \propto (\text{二項分布}) \times (\text{ベータ分布})
\end{align}
ここで,二項分布の形は分かっていますので,求めたいパラメータ$\mu$に関する部分のみ抽出して代入してみます。
(\text{ベータ分布}) \propto \mu^k (1-\mu)^{n-k} \times (\text{ベータ分布})
\end{align}
したがって,ベータ分布は以下のような形になっていれば都合が良いことが推測されます。
(\text{ベータ分布}) &= C \mu^a (1-\mu)^b
\end{align}
ただし,$C$は正規化項を表します。あとは,ベータ分布が確率密度関数の定義を満たすように,積分して$1$になるような正規化項$C$を求めてあげるだけです。さて,まずはベータ分布の形を決める部分を$\mu$に関して積分したものを$B(a+1, b+1)$とおきます。なお,$B(a,b)$はベータ関数と呼ばれています。なぜ$a+1$,$b+1$と中途半端な定数を用いているのかというと,後でベータ関数をガンマ関数で表す際に綺麗な形にするためです。差し当たりは定義として受け入れてください。
さて,ベータ関数を計算していきましょう。$\mu$の定義域は$[0,1]$ですので,ベータ関数の積分範囲も$[0,1]$になります。
B(a+1, b+1) &= \int_{0}^{1}\mu^a (1-\mu)^b d\mu
\end{align}
改めてベータ分布の積分を書き直すと,以下のように表されます。
\int_{0}^{1}(\text{ベータ分布})d\mu &= C\int_{0}^{1}\mu^a (1-\mu)^b d\mu \\[0.7em]
&= C B(a+1,b+1)
\end{align}
したがって,正規化定数をベータ関数を用いて表すことができます。
C &= \frac{1}{B(a+1, b+1)}
\end{align}
以下では,$B(a+1, b+1)$を計算していきます。結論から言うと,ベータ関数はガンマ関数の積を用いて表すことができます。
ベータ関数は,ガンマ関数を用いて以下のように表される。
B(a-1,b-1) &= \frac{\Gamma(a)\Gamma(b)}{\Gamma(a+b)}
\end{align}
したがって,ベータ分布の確率密度関数$f$は以下のようになります。
f(\mu) &= \frac{\Gamma(a+b)}{\Gamma(a)\Gamma(b)}
\mu^{a-1} (1-\mu)^{b-1} \label{ベータ分布}
\end{align}
モーメント母関数
通常,モーメント母関数はモーメント母関数の定義に従って計算していきます。しかし,ベータ分布のモーメント母関数は複雑な計算を要するため,あまり利用されていません。本稿でもそれに倣い,割愛することにします。
平均・分散
連続分布の平均と分散を求めるためには,モーメント母関数の性質を利用します。しかし,ベータ分布のモーメント母関数は複雑な形をしているため,ここでは平均と分散の定義に従って愚直に計算していきます。パズル問題的な感覚でスルスルと求めていく感覚を身に付けましょう。利用するのは以下の関係式のみです。
B(a,b) &= \frac{\Gamma(a)\Gamma(b)}{\Gamma(a+b)} \\[0.7em]
\Gamma(a+1) &= a\Gamma(a)
\end{align}
実際に計算していきます。まず,原点周りの一次モーメント,すなわち期待値を求めます。
E[X] &= \frac{1}{B(a, b)}\int_{0}^{1}x\cdot x^{a-1}(1-x)^{b-1} dx \\[0.7em]
&= \frac{1}{B(a, b)}\cdot B(a+1, b) \\[0.7em]
&= \frac{\Gamma(a+b)}{\Gamma(a)\Gamma(b)} \cdot
\frac{\Gamma(a+1)\Gamma(b)}{\Gamma(a+b+1)} \\[0.7em]
&= \frac{\Gamma(a+b)}{\Gamma(a)}\cdot
\frac{a\Gamma(a)}{(a+b)\Gamma(a+b)} \\[0.7em]
&= \frac{a}{a+b}
\end{align}
まさに,ガンマ関数を階乗的な感覚で次数を落としていって約分していくパズルです。
次に,原点周りの二次モーメントも求めていきます。
E[X^2] &= \frac{1}{B(a, b)}\int_{0}^{1}x^2\cdot x^{a-1}(1-x)^{b-1} dx \\[0.7em]
&= \frac{1}{B(a, b)}\cdot B(a+2, b) \\[0.7em]
&= \frac{\Gamma(a+b)}{\Gamma(a)\Gamma(b)} \cdot
\frac{\Gamma(a+2)\Gamma(b)}{\Gamma(a+b+2)} \\[0.7em]
&= \frac{\Gamma(a+b)}{\Gamma(a)}\cdot
\frac{(a+1)a\Gamma(a)}{(a+b+1)(a+b)\Gamma(a+b)} \\[0.7em]
&= \frac{(a+1)a}{(a+b+1)(a+b)}
\end{align}
最後に,原点周りの一次モーメントと原点周りの二次モーメントから分散を求めます。
V[X] &= E[X^2] - E[X]^2 \\[0.7em]
&= \frac{(a+1)a}{(a+b+1)(a+b)} - \left(\frac{a}{a+b}\right)^2 \\[0.7em]
&= \frac{ab}{(a+b)^2(a+b+1)}
\end{align}
再生性
再生性を示すためには,再生性を示したい分布に従う独立な二つの確率変数を考え,その和のモーメント母関数を計算したときに,パラメータが和の形になっていることを示します。しかし,ベータ分布のモーメント母関数は複雑な形をしており,積をとっても同じ形が出現しないため,ベータ分布は再生性を持ちません。
ロードマップ
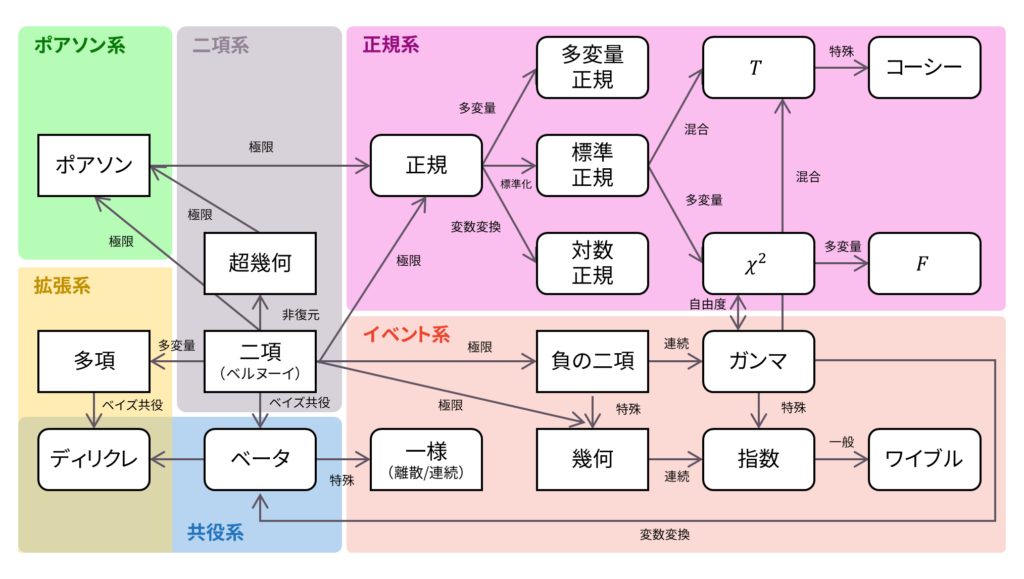
さて,ロードマップに戻りましょう。 ベータ分布は,二項分布の共役事前分布として導出できましたね。同時に,ガンマ分布に従う確率変数を利用した変数変換を通じても導出することができました。以下の内容も参考になるでしょう。
参考文献
本稿の執筆にあたり参考にした文献は,以下でリストアップしております。


コメント