本記事は「これなら分かる!はじめての数理統計学」シリーズに含まれます。
不適切な内容があれば,記事下のコメント欄またはお問い合わせフォームよりご連絡下さい。
多変量正規分布
f_{\mX}(\vx) &= \frac{1}{(2\pi)^{D/2}|\Sigma|^{1/2}}\exp \left\{ -\frac{1}{2}(\vx-\vmu)^T \Sigma^{-1}(\vx-\vmu) \right\} \\[0.7em]
M_{\mX}(\vt) &= \exp\left( \vmu^T\vt + \frac{1}{2}\vt^T\Sigma\vt \right) \\[0.7em]
E[\mX] &= \vmu \\[0.7em]
V[\mX] &= \Sigma
\end{align}
多変量正規分布は正規分布を$D$次元に多変量化した確率分布であり,以下のベクトル
\mX &= [X_{1}, \ldots, X_{D}] \\[0.7em]
\vmu &= [\mu_{1}, \ldots, \mu_{D}]
\end{align}
と,分散共分散行列$\Sigma \in \bbR^{D \times D}$を用いて定義されます。多変量正規分布に従う確率変数$\mX$に対し,実現値は
\vx \in \bbR^{D}
\end{align}
であり,モーメント母関数の変数は$\vt \in \bbR^{D}$とします。多変量正規分布は再生性を持ち,ロードマップ中では正規分布の多変量化に相当します。
確率密度関数
正規分布の確率密度関数の導出方法には,大きく二つの方法があります。
- 正規分布を多次元に拡張する
- 予め定義された多変量正規分布のモーメント母関数から導出する
正規分布の拡張
本節では,正規分布を多変量に拡張することで多変量正規分布の確率密度関数を導出していきます。正規分布を多次元に拡張するためには,スカラーであった確率変数をベクトルに拡張する必要があります。そこで,入力として以下のベクトルを考えます。
\mZ &= [Z_1, \cdots, Z_D]^T \\[0.7em]
\vz &= [z_1, \ldots, z_D]^T
\end{align}
ただし,$\mZ$を確率変数,$\vz$を実現値とします。私たちの目標は,$Z_1, \cdots, Z_D$がそれぞれ正規分布に従うときに$\mZ$が従う確率密度関数を導出することです。最初から一般の正規分布を扱うのは少し面倒なので,まずは母集団として独立な標準正規分布を考えた後に,確率変数の変数変換を用いて正規分布に一般化することにします。
$Z_1, \cdots, Z_D$がそれぞれ独立に標準正規分布に従うとします。すると,独立の定義より,$\mZ$の同時確率密度関数$g$は以下のようになります。
g(\vz) &= \prod_{d=1}^{D}g(z_d) \\[0.7em]
&= \frac{1}{(2\pi)^{D/2}}\exp \left( -\frac{1}{2}\sum_{d=1}^{D} z_{d}^2 \right)\\[0.7em]
&= \frac{1}{(2\pi)^{D/2}}\exp \left( -\frac{1}{2} \vz^T \vz \right)
\label{norm_gauss}
\end{align}
一般の正規分布に拡張するため,線形変換を用いて定義される確率変数$X$を導入します。
\mX &= A \mZ + \vmu \\[0.7em]
\vmu &= [\mu_1, \ldots, \mu_D]^T \\[0.7em]
\vx &= [x_1, \ldots, x_D]^T
\end{align}
ただし,$A \in \bbR^{D \times D}$は正則であり,$\vmu$は期待値を結合したベクトル,$\vx$は確率変数$\mX$の実現値を表すものとします。
確率変数$X$は線形変換$A$を用いて定義されていますので,$Z_1,\ldots,Z_D$の独立性は失われます。よく勘違いされるのですが,多変量正規分布に従う確率変数$X_1,\ldots,X_D$はそれぞれ独立ではありません。分散共分散行列が対角行列である場合にそれぞれの共分散が$0$となり,$X_1,\ldots,X_D$は独立になります。詳しくは独立と無相関の関係をご覧ください。
$A$は正則ですので,確率変数$\mZ$は以下のように表されます。
\mZ &= A^{-1}(\mX - \vmu)
\label{jacobian}
\end{align}
式($\ref{norm_gauss}$)に式($\ref{jacobian}$)を代入すれば一件落着かというと,そう甘くはありません。確率密度関数は積分を利用して定義されているため,ヤコビアンを利用して変換前後の辻褄を合わせなくてはいけないのです。ヤコビアンを求めるためには,逆変換($\ref{jacobian}$)に加えて$\mW=\mY$という恒等変換を持ち出すと分かりやすいです。
\begin{cases}
\mZ = h_1(\mX, \mY) = A^{-1}(\mX-\vmu) \\[0.7em]
\mW = h_2(\mX, \mY) = \mY
\end{cases}
\end{align}
実際にヤコビアンを求めていきましょう。
|J|
&=
\abs \left|
\begin{array}{cc}
\partial h_1(\mX, \mY) / \partial \mX & \partial h_1(\mX, \mY) / \partial \mY \\
\partial h_2(\mX, \mY) / \partial \mX & \partial h_2(\mX, \mY) / \partial \mY \\
\end{array}
\right| \\[0.7em]
&= \abs\left|
\begin{array}{cc}
A^{-1} & O_{D} \\
O_D & I_{D} \\
\end{array}
\right|
= \abs|A^{-1}|
= \abs|A|^{-1}
\end{align}
ただし,$\abs$は絶対値,$|\cdot|$は行列式を表し,逆行列の行列式は行列式の逆行列と等しくなることを利用しました。すると,確率変数の変数変換より以下が成り立ちます。
f(\vx) &= g(\vz) \cdot \abs |A|^{-1} \label{f_g}
\end{align}
式($\ref{f_g}$)に式(\ref{norm_gauss})と式($\ref{jacobian}$)を代入します。ただし,逆行列と転置が交換できること(\ref{inverse_transpose})と積の行列式の性質($\ref{product_inverse}$)を利用します。
(S^{-1})^{T} &= (S^{T})^{-1} \label{inverse_transpose} \\[0.7em]
(ST)^{-1} &= T^{-1} S^{-1} \label{product_inverse}
\end{align}
実際に計算を進めてみましょう。
f(\vx) &= \frac{1}{(2\pi)^{D/2}} \exp\left\{ -\frac{1}{2} (\vx - \vmu)^T (A^{-1})^T A^{-1}(\vx - \vmu) \right\}\cdot \abs |A|^{-1} \\[0.7em]
&= \frac{1}{(2\pi)^{D/2}} \exp\left\{ -\frac{1}{2} (\vx - \vmu)^T (A^{T})^{-1} A^{-1}(\vx - \vmu) \right\}\cdot\abs |A|^{-1}\\[0.7em]
&= \frac{1}{(2\pi)^{D/2}} \exp\left\{ -\frac{1}{2} (\vx - \vmu )^T ( A A^T)^{-1}(\vx - \vmu) \right\}\cdot \abs |A|^{-1} \label{before_gauss}
\end{align}
あと一歩です。$AA^T$と$\abs |A|^{-1}$を求めることができれば,$f(\vx)$の導出が完了します。まずは,$AA^T$の導出から始めましょう。
$AA^T$の導出
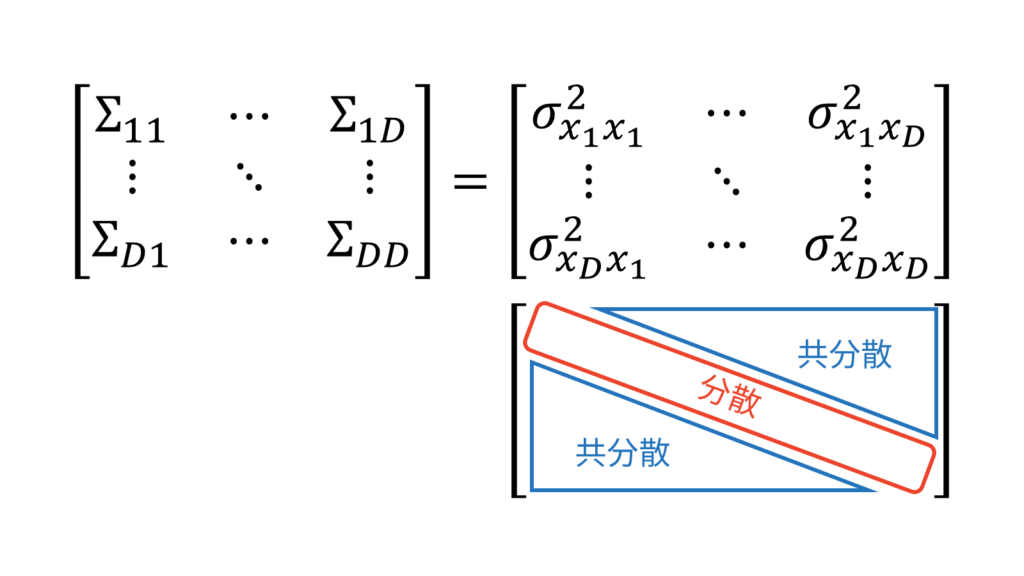
結論からお伝えすると,$AA^T$は$\mX$の分散共分散行列$\Sigma$と等しくなります。分散共分散行列というのは,複数の確率変数の分散と共分散をまとめて表すことのできる行列です。共分散は確率変数の順番に依存しませんので,分散共分散行列は対称半正定値行列になります。
やや天下り的ですが,分散の定義より以下が成り立つことに注目します。
V[\mX] &= E\left[(\mX-\vmu)(\mX-\vmu)^T\right]\\[0.7em]
&= E\left[A \mZ (A \mZ)^T\right]\\[0.7em]
&= E\left[A \mZ \mZ^T A^T\right] \\[0.7em]
&= A E\left[\mZ \mZ^T\right] A^T \label{V_X}
\end{align}
ただし,$A$の要素は定数であるため,期待値$E$の外に出せることに注意して下さい。すると,$E[\mZ \mZ^T]$を求める必要が出てきました。先ほど$V[\mX]$を持ち出したときと同様に,分散の定義から以下が成り立ちます。
V[\mZ] &= E\left[(\mZ-\vzero)(\mZ-\vzero)^T\right] \\[0.7em]
&= E\left[\mZ \mZ^T\right] \\[0.7em]
&\triangleq \Sigma_z \label{Sigma_z}
\end{align}
ただし,$\mZ$の分散共分散行列$V[\mZ] \in \bbR_{+}^{D \times D}$を$\Sigma_z$と定義しました。
$\triangleq$は定義を表す記号です。
$Z_1,\ldots,Z_D$はそれぞれ独立に標準正規分布に従うことに注意すると,$\Sigma_z$の共分散は$0$,分散は$1$となります。すると,$\Sigma_z$は$D$次元単位行列$I_{D}$となります。
\Sigma_z &= I_{D} \label{Sigma_z_I}
\end{align}
式($\ref{V_X}$)に式($\ref{Sigma_z}$)と式($\ref{Sigma_z_I}$)を代入します。ただし,$\Sigma_z$と同様に$\mX$の分散共分散行列を新しく$\Sigma$とおきます。
V[X] &= A E[\mZ \mZ^T] A^T \\[0.7em]
&= A \Sigma_z A^T \\[0.7em]
&= A A^T \\[0.7em]
&\triangleq \Sigma
\end{align}
以上より,$AA^T$が$\mX$の分散共分散行列と等しくなることが分かりました。
AA^T &= \Sigma \label{AA_transpose}
\end{align}
$\abs |A|^{-1}$の導出
最後に$\abs |A|^{-1}$を求めましょう。いま,私たちは$AA^T$が$\Sigma$と等しいことを知っていますので,とりあえず$\abs|AA^T|$を変形してみましょう。
\abs |\Sigma| &= |\Sigma| \\[0.7em]
&= \abs|A A^T|\\[0.7em]
&= \abs|A| \cdot \abs|A^T|\\[0.7em]
&= \abs|A| \cdot \abs|A|^T\\[0.7em]
&= \abs|A| \cdot \abs|A| \\[0.7em]
&= \left( \abs|A| \right)^2
\end{align}
ただし,積の行列式は行列式の積であることと,転置の行列式は行列式の転置であること,行列式はスカラーであること,さらに半正定値行列の行列式に関する以下の性質を利用しました。
対称行列$\Sigma$が半正定値ならば$|\Sigma|\geq 0$
すると,$\abs |A|$を求めることができます。
\abs |A| &= |\Sigma|^{1/2}
\end{align}
以上より,$\abs |A|^{-1}$が求められました。
\abs |A|^{-1} &= |\Sigma|^{-1/2} \label{abs_A}
\end{align}
式($\ref{AA_transpose}$)と式($\ref{abs_A}$)を式($\ref{before_gauss}$)に代入しましょう。
f(\vx) &= \frac{1}{(2\pi)^{D/2}} \exp\left\{ -\frac{1}{2} (\vx - \vmu )^T ( A A^T)^{-1}(\vx - \vmu) \right\} \cdot \abs |A|^{-1}\\[0.7em]
&= \frac{1}{(2\pi)^{D/2} |\Sigma|^{1/2}} \exp\left\{ -\frac{1}{2} (\vx - \vmu )^T \Sigma^{-1}(\vx - \vmu) \right\}
\end{align}
以上で,多変量正規分布の確率密度関数が導出できました。
モーメント母関数に基づく導出
本節では,予め定められたモーメント母関数に基づいて多変量正規分布の確率密度関数を導出していきます。
確率密度関数が与えられたもとでモーメント母関数を求める方法は,本項の下部に記載しております。
$X$が$D$次元正規分布に従うとは,ベクトル$\vmu \in \bbR^{D}$と対称半正定値行列$\Sigma \in \bbR_{+}^{D \times D}$が存在して,モーメント母関数が
M_{\mX}(\vt) &= E\left[\exp\left(\vt^T \mX\right)\right] \\[0.7em]
&= \exp\left( \vmu^T \vt + \frac{1}{2}\vt^T \Sigma \vt \right)
\label{多変量正規分布のモーメント母関数}
\end{align}
であることで定義され,以下のように表されます。
X &\sim \N (\vmu, \Sigma)
\end{align}
なお,モーメント母関数は以下の行列指数関数(\ref{定義:行列指数関数})を利用して冪級数で表されることもあります。
M_{\mX}(\vt)
&=1 +\left( \vmu^T\vt + \frac{1}{2}\vt^T\Sigma\vt\right)+\left(\vt^{T}\vmu\vmu^{T}\vt\right. + \cdots\\[0.7em]
\end{align}
行列$X \in \bbR^{D \times D}$の指数関数は,以下の冪級数で定義される。
e^{X} &= \sum_{d=0}^{\infty} \frac{1}{d!} X^{d} \label{定義:行列指数関数}
\end{align}
行列指数関数は複素行列に対しても同様に定義されます。
ここからは,モーメント母関数に基づく多変量正規分布の定義を用いて多変量正規分布の確率密度関数を導出しましょう。多変量正規分布の線形変換を用いて,多変量正規分布の独立性が成り立つ状況にうまく誘導することで,同時確率密度関数が$1$次元正規分布の確率密度関数の積となることを利用します。
多変量正規分布の独立性が成り立つ状況というのは,分散共分散行列を$D_1$次元と$D_2=D-D_1$次元の小行列に分解したときに,分散共分散行列が対角行列となるケースでした。そこで,$D_1=1,\ldots,D-1$に対して逐次的に多変量正規分布の独立性に関する定理を適用すると,分散共分散行列が対角行列のときに$D$個の確率変数がそれぞれ独立であることが分かります。
ここで,$\mX \sim \N(\vmu, \Sigma)$に対して,分散共分散行列$\Sigma$を対角行列にする方法を考えます。$1$次元正規分布の標準化の類推から,
\mZ &= \Sigma^{-1/2}(\mX-\vmu) \label{標準化} \\[0.7em]
&= \Sigma^{-1/2}\mX - \Sigma^{-1/2}\vmu
\end{align}
という線形変換を考えればよさそうです。実際に,多変量正規分布の線形変換に関する定理を利用すると,
\mZ &\sim \N\left( \Sigma^{-1/2}\vmu - \Sigma^{-1/2}\vmu, \Sigma^{-1/2}\Sigma \Sigma^{-1/2} \right)\\[0.7em]
&= \N\left( \vzero_D, I_D \right)
\end{align}
となります。ただし,$\vzero_D$は$D$次元縦ゼロベクトル,$I_D$は$D$次元単位行列を表します。すなわち,式($\ref{標準化}$)を用いることで,確率変数$\mX$が標準化されていることを確認できました。変換後の$\mZ$が従う多変量正規分布の分散共分散行列が対角行列になりましたので,$D$個の確率変数$Z_1,\ldots,Z_D$は独立になります。したがって,$\mZ$の従う確率密度関数は以下のように表されます。
g(\vz) &= \prod_{d=1}^{D} \frac{1}{\sqrt{2\pi}}\exp\left( -\frac{1}{2}z_d^2 \right) \\[0.7em]
&= \frac{1}{(2\pi)^{D/2}}\exp\left( -\frac{1}{2}\vz^T \vz \right)
\end{align}
ここからは,「正規分布を多次元に拡張する」方針における導出方法と同様です。変換($\ref{標準化}$)は既に逆変換を表していますので,ヤコビアンを求めましょう。ヤコビアンを求めるためには,変換($\ref{標準化}$)に加えて$\mW=\mY$という恒等変換を持ち出すと分かりやすいです。
\begin{cases}
\mZ = h_1(\mX, \mY) = \Sigma^{-1}(\mX-\vmu) \\[0.7em]
\mW = h_2(\mX, \mY) = \mY
\end{cases}
\end{align}
実際にヤコビアンを求めていきましょう。
|J|
&=
\abs \left|
\begin{array}{cc}
\partial h_1(\mX, \mY) / \partial \mX & \partial h_1(\mX, \mY) / \partial \mY \\
\partial h_2(\mX, \mY) / \partial \mX & \partial h_2(\mX, \mY) / \partial \mY \\
\end{array}
\right| \\[0.7em]
&= \abs\left|
\begin{array}{cc}
\Sigma^{-1/2} & O_{D} \\
O_D & I_{D} \\
\end{array}
\right|
= |\Sigma^{-1/2}|
= |\Sigma|^{-1/2}
\end{align}
ただし,$\abs$は絶対値,$|\cdot|$は行列式を表し,逆行列の行列式は行列式の逆行列と等しくなること,および対称行列が半正定値ならば行列式が非負となる性質を利用しました。すると,確率変数の変数変換より以下が成り立ちます。
f(\vx) &= g(\vz) \cdot |\Sigma|^{-1/2} \\[0.7em]
&= \frac{1}{(2\pi)^{D/2}|\Sigma|^{1/2}}\exp\left[ -\frac{1}{2}\left\{\Sigma^{-1/2}(\mX-\vmu)\right\}^T \Sigma^{-1/2}(\mX-\vmu) \right] \\[0.7em]
&= \frac{1}{(2\pi)^{D/2}|\Sigma|^{1/2}}\exp\left\{ -\frac{1}{2}(\mX-\vmu)^T \Sigma^{-1/2} \Sigma^{-1/2}(\mX-\vmu) \right\} \\[0.7em]
&= \frac{1}{(2\pi)^{D/2}|\Sigma|^{1/2}}\exp\left\{ -\frac{1}{2}(\mX-\vmu)^T \Sigma^{-1}(\mX-\vmu) \right\}
\end{align}
以上で,モーメント母関数に基づく多変量正規分布の定義を利用した確率密度関数の導出が完了しました。
平均・分散
連続分布の平均と分散を求めるためには,モーメント母関数の性質を利用します。しかし,今回は変数が多変量になっていますので,多変量モーメント母関数の性質を多変量正規分布のモーメント母関数に適用します。まず,一次モーメント,すなわち期待値を求めます。
E[\mX] &= M^{\prime}_{\mX}(\vzero) \\[0.7em]
&= \left. \vmu + \Sigma\vt + \cdots \right|_{\vt = \vzero} \\[0.7em]
&= \vmu \label{一次モーメント}
\end{align}
ただし,行列の微分に関する以下の公式を用いました。
\frac{\partial}{\partial \vx} \left(\va^T \vx\right) &= \va \\[0.7em]
\frac{\partial}{\partial \vx} \left(\vx^TA \vx\right) &= (A+A^T)\vx
\end{align}
続いて,二次モーメントを求めます。
E[\mX\mX^T] &= M^{\prime\prime}_{\mX}(\vzero) \\[0.7em]
&= \left. \Sigma + \vmu\vmu^T + \cdots \right|_{\vt = \vzero} \\[0.7em]
&= \Sigma + \vmu\vmu^T \label{二次モーメント}
\end{align}
最後に,一次モーメントと二次モーメントから分散共分散行列を求めます。
E\left[ \left( \mX - E[\mX] \right)\left( \mX - E[\mX] \right)^T \right]
&= E\left[\mX \mX^T\right] - E[\mX]E\left[\mX\right]^T \\[0.7em]
&= \Sigma + \vmu\vmu^T - \vmu\vmu^T \\[0.7em]
&= \Sigma
\end{align}
再生性
再生性を示すためには,再生性を示したい分布に従う独立な二つの確率変数を考え,その和のモーメント母関数を計算したときに,パラメータが和の形になっていることを示します。いま,二つの独立な確率変数
\mX &\sim \N(\mu_x, \Sigma_x) \\[0.7em]
\mY &\sim \N(\mu_y, \Sigma_y)
\end{align}
を考えます。このとき,$X+Y$のモーメント母関数を計算します。
M_{\mX+\mY}(t) &= M_{\mX}(\vt) \cdot M_{\mY}(\vt) \\[0.7em]
&= \exp\left( \vmu_x^T \vt + \frac{1}{2}\vt^T \Sigma_x \vt \right) \cdot \exp\left( \vmu_y^T \vt + \frac{1}{2}\vt^T \Sigma_y \vt \right)\\[0.7em]
&= \exp\left\{ \left( \vmu_x^T + \vmu_y^T\right) \vt + \frac{1}{2}\vt^T \left(\Sigma_x + \Sigma_y\right) \vt \right\}
\end{align}
これは,$\mX+\mY$のモーメント母関数が正規分布のモーメント母関数であることを示しています。つまり,
\mX+\mY\sim \N(\vmu_x + \vmu_y, \Sigma_x + \Sigma_y)
\end{align}
であり,多変量正規分布の再生性を示しています。
補足
多変量正規分布の確率密度関数からモーメント母関数を求めるためには,平方完成を利用します。モーメント母関数の定義より,
M_{X}(\vt) &= E[e^{\vt^{T}X}] = \frac{1}{(2\pi)^{D/2}|\Sigma|^{1/2}}\exp \left\{ \vt^{T}\vx -\frac{1}{2}(\vx-\vmu)^T \Sigma^{-1}(\vx-\vmu) \right\}\label{正規分布_モーメント母関数}
\end{align}
となります。指数部分だけに着目して平方完成すると,
&\vt^{T}\vx -\frac{1}{2}(\vx-\vmu)^T \Sigma^{-1}(\vx-\vmu)\notag\\[0.7em]
&= \vt^{T}\vx -\frac{1}{2}(\vx^{T}\Sigma^{-1}\vx-2\vmu^{T}\Sigma^{-1}\vx+\vmu^{T}\Sigma^{-1}\vmu)\\[0.7em]
&= -\frac{1}{2}\left\{\vx^{T}\Sigma^{-1}\vx-2(\vmu^{T}+\vt^{T}\Sigma)\Sigma^{-1}\vx+\vmu^{T}\Sigma^{-1}\vmu\right\}\\[0.7em]
&= -\frac{1}{2}\left\{\vx^{T}\Sigma^{-1}\vx-2(\vmu^{T}+(\Sigma\vt)^{T})\Sigma^{-1}\vx+\vmu^{T}\Sigma^{-1}\vmu\right\}\\[0.7em]
&= -\frac{1}{2}\left\{\vx^{T}\Sigma^{-1}\vx-2(\vmu+\Sigma\vt)^{T}\Sigma^{-1}\vx+\vmu^{T}\Sigma^{-1}\vmu\right\}\\[0.7em]
&= -\frac{1}{2}\left[\left\{\vx-(\vmu+\Sigma\vt)\right\}^{T}\Sigma^{-1}\left\{\vx-(\vmu+\Sigma\vt)\right\}-2\vt^{T}\vmu-\vt^{T}\Sigma\vt\right]\\[0.7em]
&=\vt^{T}\vmu+\frac{1}{2}\vt^{T}\Sigma\vt-\frac{1}{2}\left(\vx-\vmu-\Sigma\vt\right)^{T}\Sigma^{-1}\left(\vx-\vmu-\Sigma\vt\right)
\end{align}
が得られます。第三項目は多変量正規分布の指数部となっており,モーメント母関数の定義($\ref{正規分布_モーメント母関数}$)に代入すると$1$となるため,第一項目と第二項目が残ります。したがって,
M_{X}(\vt) &= \exp\left(\vt^{T}\vmu+\frac{1}{2}\vt^{T}\Sigma\vt\right)
\end{align}
が得られます。
ロードマップ
さて,ロードマップに戻りましょう。 多変量正規分布は正規分布を多変量化して得られる分布です。多変量化のプロセスとしては,標準正規分布を多変量化してから変数変換を施すのでした。多変量正規分布の導出には,モーメント母関数由来の定義もありましたね。以下の内容も参考になるでしょう。
参考文献
本稿の執筆にあたり参考にした文献は,以下でリストアップしております。


コメント
コメント一覧 (4件)
早々にご対応いただきましてありがとうございます。
(他のページでコメント入力してしまい、分かりにくくなってしまい申し訳ございませんでした。)
Y=YのところもW=Yと変更していただいたようですね。
また式'(17)でまとめていただき、より理解が深まりました。
変数変換 (X, Y) → (Z, W) ということですね。
多変量正規分布の確率密度関数を求めるための2つのアプローチですが
① AA^T(すなわち分散共分散行列)を使う方法
② モーメント母関数を使う方法
のいずれにおきましても、変数変換やヤコビアンの導出方法は同様でしょうか。
そうであれば式(60) (61) (62) の Z および δZ もそれぞれ X と δX
となりますでしょうか。
数理統計初学者さま
ご指摘ありがとうございます。
対応遅くなりました。
おっしゃる通りですので,本文を修正しました。
また何か違和感がある箇所があればお気軽にコメントください!
zukaさん
GW中にも関わらず、迅速な改訂ありがとうございます!
Academaidの全てのページに言えることだと思いますが、Webデザインが本当に素晴らしく、数式もとても見やすく美しいです。
$AA^T$の導出も他の教科書ではなかなか理解できずにいましたが、式(26)から式(38)の流れは線形代数もほぼ初学者(大学の教養で何とか単位を取れたレベルでその後学習歴なし)の小生にとりまして、まさに目から鱗でした。バイブルと言われる教科書でも、大学での線形代数の知識を前提としているせいか、式(28)=式(36)へといきなり記載されていることが多いのですが、本当に丁寧に解説していただいて感謝感謝です。
モーメント母関数を用いた解説でも、他の教科書では、つい流し読みしがちですが、しっかりと数式を追うことができました。本当にありがとうございます。
数理統計初学者 さま
嬉しいお言葉ありがとうございます。
引き続き記事の執筆活動は続けてまいりますので,ご愛読いただけますと幸いです。