【徹底解説】標準ロジスティック分布とは

2022年6月23日

本記事は「これなら分かる！はじめての数理統計学」シリーズに含まれます。

不適切な内容があれば，記事下のコメント欄またはお問い合わせフォームよりご連絡下さい。

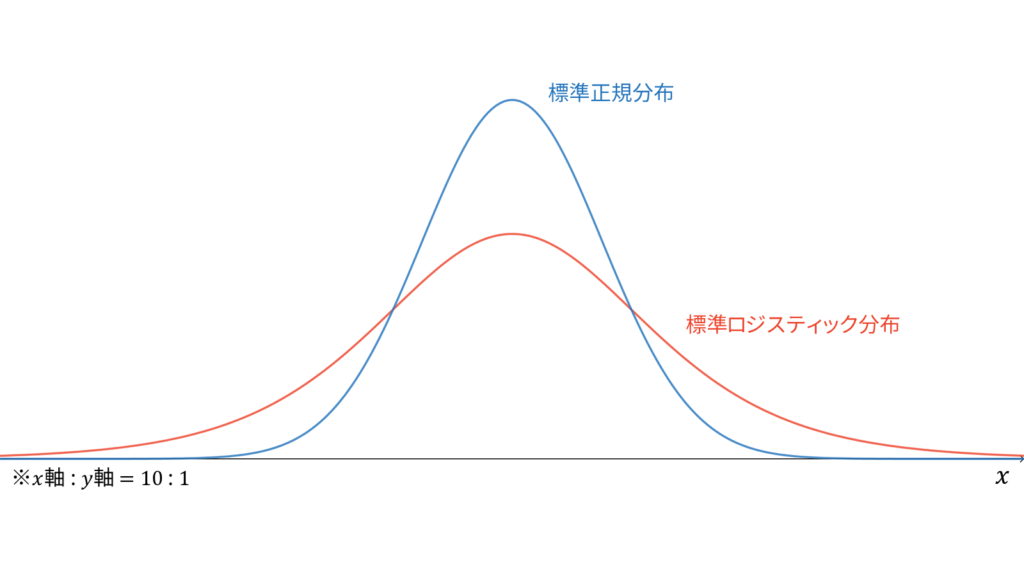
標準ロジスティック分布

\begin{align}
f_{X}(x) &= \frac{e^{-x}}{\left(1+e^{-x}\right)^2} \\[0.7em]
M_{X}(t) &= \Gamma(1+t) \Gamma(1-t) \\[0.7em]
E[X] &= 0 \\[0.7em]
V[X] &= \frac{\pi^2}{3}
\end{align}

ただし，$\Gamma(\cdot)$はガンマ関数を表す。

\begin{align}
\Gamma(n) &= \int_0^{\infty}t^{n-1}e^{-t}dt
\end{align}

標準ロジスティック分布は，累積分布関数が標準シグモイド関数となる確率分布として定式化されます。標準ロジスティック分布に従う確率変数$X$に対し，実現値は

\begin{align}
x \in \bbR
\end{align}

であり，モーメント母関数の変数は$|t|<1$とします。正規分布とよく似た形をしていますが，より裾の長い分布になっています。

確率密度関数

標準ロジスティック分布は，累積分布関数が標準シグモイド関数となる確率分布として定式化されます。

\begin{align}
F_{X}(x) &= \frac{1}{1+e^{-x}}
\end{align}

したがって，確率密度関数は以下のように導出されます。

\begin{align}
f_{X}(x) &= \frac{d}{dx} \left( \frac{1}{1+e^{-x}}\right) \\[0.7em]
&= \frac{e^{-x}}{\left(1+e^{-x}\right)^2}
\end{align}

モーメント母関数

モーメント母関数の定義に従って計算していきます。

\begin{align}
M_{X}(t) &= E\left[e^{tx}\right] \\[0.7em]
&= \int_{-\infty}^{\infty} e^{tx}\frac{e^{-x}}{\left(1+e^{-x}\right)^2} dx \label{モーメント母関数}
\end{align}

ここで，標準ロジスティック分布の累積分布関数が標準シグモイド関数であったことに着目しましょう。まず，以下のように置換します。

\begin{align}
u &= \frac{1}{1+e^{-x}} \label{置換}
\end{align}

これは，標準シグモイド関数を$u$と置くことを意味しています。後のために，$e^x$を$u$で表しておきましょう。

\begin{align}
e^{x} &= \frac{u}{1-u} \label{e^x}
\end{align}

また，標準シグモイド関数の性質としてよく知られているように，$u$を$x$で微分すると，

\begin{align}
\frac{du}{dx} &= u(1-u) \label{シグモイドの微分}
\end{align}

となります。式($\ref{シグモイドの微分}$)はベータ関数の被積分関数の形をしていますので，式($\ref{置換}$)の置換により標準ロジスティック分布のモーメント母関数($\ref{モーメント母関数}$)がベータ関数を用いて表せることを期待します。実際に，式($\ref{e^x}$)と式($\ref{シグモイドの微分}$)に注意すると，

\begin{align}
M_{X}(t) &= \int_{0}^{1} \left( \frac{u}{1-u} \right)^t du \label{1} \\[0.7em]
&= \int_{0}^{1} u^{(1+t)-1}(1-u)^{(1-t)-1} du \\[0.7em]
&= B(1+t, 1-t) \label{2}\\[0.7em]
&= \frac{\Gamma(1+t)\Gamma(1-t)}{\Gamma(2)} \label{3}\\[0.7em]
&= \Gamma(1+t)\Gamma(1-t)\label{4}
\end{align}

と計算できます。ただし，式($\ref{1}$)から式($\ref{2}$)はベータ関数の定義，式($\ref{2}$)から式($\ref{3}$)はベータ関数とガンマ関数の関係，式($\ref{3}$)から式($\ref{4}$)はガンマ関数と階乗の関係を利用しました。

平均・分散

連続分布の平均と分散を求めるためには，モーメント母関数の性質を利用します。まず，原点周りの一次モーメント，すなわち期待値を求めます。

\begin{align}
E[X] &= \left.M^{\prime}_{X}(t) \right|_{t=0} \\[0.7em]
&= \left.\left\{ \Gamma^{\prime}(1+t)\Gamma(1-t)-\Gamma(1+t)\Gamma^{\prime}(1-t) \right\}\right|_{t=0} \\[0.7em]
&= \Gamma^{\prime}(1)\Gamma(1)-\Gamma(1)\Gamma^{\prime}(1) \\[0.7em]
&= 0
\end{align}

続いて，原点周りの二次モーメントを求めます。

\begin{align}
E\left[X^2\right] &= \left.M^{\prime\prime}_{X}(t) \right|_{t=0} \\[0.7em]
&= \left.\left\{ \Gamma^{\prime\prime}(1+t)\Gamma(1-t)-2\Gamma^{\prime}(1+t)\Gamma^{\prime}(1-t)+\Gamma(1+t)\Gamma^{\prime\prime}(1-t) \right\}\right|_{t=0} \\[0.7em]
&= 2\left\{ \Gamma^{\prime\prime}(1)-\Gamma^{\prime}(1)\Gamma^{\prime}(1)\right\} \label{二次モーメント}
\end{align}

ただし，$\Gamma(1)=1$を利用しました。ここで，やや天下り的なのですが，式($\ref{二次モーメント}$)はポリガンマ関数の級数表示を用いて計算することができます。順を追って説明していきます。まず，ディガンマ関数$\psi(x)$は対数ガンマ関数の導関数として定義されます。

\begin{align}
\psi(x) &= \frac{d}{dx}\log \Gamma(x) \\[0.7em]
&= \frac{\Gamma^{\prime}(x)}{\Gamma(x)}
\end{align}

ポリガンマ関数は，ディガンマ関数の$m$回微分として定義されます。

\begin{align}
\psi^{(m)}(x) &= \frac{d^{m}}{dx^{m}}\psi(x)
\end{align}

$m=1$のポリガンマ関数を計算してみましょう。

\begin{align}
\psi^{(1)}(x) &= \frac{d}{dx}\left(\frac{\Gamma^{\prime}(x)}{\Gamma(x)}\right) \\[0.7em]
&= \frac{\Gamma^{\prime\prime}(x)\Gamma(x)-\left\{\Gamma^{\prime}(x)\right\}^2}{\left\{\Gamma(x)\right\}^2}
\end{align}

分子に式($\ref{二次モーメント}$)の形が出現しました。$x=1$を代入してみましょう。

\begin{align}
\Gamma^{\prime\prime}(1)-\Gamma^{\prime}(1)\Gamma^{\prime}(1)
&= \psi^{(1)}(1)\cdot \left\{\Gamma(1)\right\}^2 \\[0.7em]
&= \psi^{(1)}(1)\label{整理後}
\end{align}

ただし，$\Gamma(1)=1$を利用しました。ここで，ポリガンマ関数の級数表示を用いると，

\begin{align}
\psi^{(1)}(1) &= (-1)^{2}\cdot 1!\cdot \sum_{n=0}^{\infty}\frac{1}{(n+1)^2} \\[0.7em]
&= \zeta(2)
\end{align}

となります。ただし，$\zeta(s)$はリーマンゼータ関数を表します。$\zeta(2)$の値はバーゼル問題としても知られていて，オイラーによって値が求められました。証明は別ページで行うことにして，結果のみを用います。

\begin{align}
\psi^{(1)}(1) &= \frac{\pi^2}{6} \label{オイラー}
\end{align}

式($\ref{オイラー}$)を式($\ref{整理後}$)に代入し，その結果を式($\ref{二次モーメント}$)に代入すると，以下が得られます。

\begin{align}
E[X^2] &= \frac{\pi^2}{3}
\end{align}

最後に，一次モーメントと二次モーメントから分散を求めます。

\begin{align}
V[X] &= E[X^2] - E[X]^2 \\[0.7em]
&= \frac{\pi^2}{3}-0 \\[0.7em]
&= \frac{\pi^2}{3}
\end{align}

再生性

再生性を示すためには，再生性を示したい分布に従う独立な二つの確率変数を考え，その和のモーメント母関数を計算したときに，パラメータが和の形になっていることを示します。ロジスティック分布のモーメント母関数の積をとっても同じモーメント母関数の形が現れないため，ロジスティック分布に再生性はありません。

ロードマップ

ロジスティック分布はロードマップには含まれていませんが，累積分布関数が標準シグモイド関数となる確率分布として導出されました。

参考文献

本稿の執筆にあたり参考にした文献は，以下でリストアップしております。

参考文献リストへ

シェアはこちらからお願いします！