本記事は「これなら分かる!はじめての数理統計学」シリーズに含まれます。
不適切な内容があれば,記事下のコメント欄またはお問い合わせフォームよりご連絡下さい。
ディリクレ分布
f_{\mX}(\vx) &= \frac{1}{B(\valpha)} \prod_{k=1}^{K} x_{k}^{\alpha_{k}-1} \\[0.7em]
E[X_k] &= \frac{\alpha_k}{\sum_{l=1}^{K} \alpha_l} \\[0.7em]
V[X_k] &= \frac{\alpha_k\left(\sum_{l=1}^{K} \alpha_l-\alpha_k\right)}{\left(\sum_{l=1}^{K} \alpha_l + 1\right)\left(\sum_{l=1}^{K} \alpha_l\right)^2}
\end{align}
ただし,$B(\cdot, \cdot)$はベータ関数を表す。
B(a, b) &= \int_0^1 x^{a-1}(1-x)^{b-1}dx
\end{align}
ディリクレ分布はベータ分布の多カテゴリ拡張であり,
\Dir (\valpha)
\end{align}
と表され,以下のベクトル
\mX &= [X_1, \ldots, X_K] \\[0.7em]
\vx &= [x_1, \ldots, x_K] \\[0.7em]
\valpha &= [\alpha_1, \ldots, \alpha_K]
\end{align}
を用いて定義されます。ただし,$\alpha_k-1\geq 0$は各カテゴリの発生回数を表し,確率変数$\mX$の実現値$\vx$は
\sum_{k=1}^{K} x_k &= 1
\end{align}
を満たします。モーメント母関数は複雑な形をしているため,あまり利用されません。ディリクレ分布は再生性を持たず,ロードマップ中ではベータ分布の多変量化に相当します。すなわち,多項分布の共役事前分布に相当します。
確率密度関数
ディリクレ分布の確率密度関数の導出方法には,大きく分けて二つあります。
- 多項分布の共役事前分布
- ガンマ分布に従う確率変数の変数変換を利用
多項分布の共役事前分布
ディリクレ分布は,多項分布の共役事前分布です。多項分布は二項分布の多カテゴリ拡張でしたので,ディリクレ分布はベータ分布の多カテゴリ拡張になります。すなわち,ベータ分布ではコインを対象としていましたが,ディリクレ分布ではサイコロを対象とするということになります。
それでは,ベータ分布のときと同様にまずはディリクレ分布の形を求めてみましょう。
(\text{ディリクレ分布}) &\propto (\text{多項分布}) \times (\text{ディリクレ分布}) \\[0.7em]
&= x_1^{\alpha_1} x_2^{\alpha_2}\ldots x_K^{\alpha_K} \times (\text{ディリクレ分布})
\end{align}
ゆえに,ディリクレ分布の確率密度関数$f(\vx)$は以下のような形をとると都合が良いです。
f(\alpha_1,\ldots, \alpha_{n-1}) &= C x_1^{\alpha_1-1} x_2^{\alpha_2-1}\ldots x_K^{\alpha_K-1}
\end{align}
ただし,$C$は正規化定数を表し,後でガンマ分布をきれいな形で扱うため指数部分は$\alpha_i-1 \geq 0$を用いました。$\alpha_i-1$は各カテゴリの発生回数を表しますので,$\alpha_i$は各カテゴリの発生回数に$1$を足した値になります。ベータ分布の結果から類推するに,正規化定数$C$は以下のような形になることが予測されます。
C &= \frac{\Gamma(\alpha_1 + \ldots + \alpha_K)}{\Gamma(\alpha_1)\ldots \Gamma(\alpha_K)}
\label{ディリクレ分布の正規化定数}
\end{align}
式($\ref{ディリクレ分布の正規化定数}$)の証明は以下の形で行います。
\int_{0}^{\infty} x_1^{\alpha_1-1} x_2^{\alpha_2-1}\ldots x_K^{\alpha_K-1} dx_1\ldots dx_{K-1}
&= \frac{\Gamma(\alpha_1)\ldots \Gamma(\alpha_K)}{\Gamma(\alpha_1+\ldots+\alpha_K)} \label{ディリクレ分布で証明したい式}
\end{align}
以上より,ディリクレ分布の確率密度関数は以下のように表されます。
f(\alpha_1,\ldots,\alpha_{n-1}) &= \frac{\Gamma(\alpha_1 + \ldots + \alpha_K)}{\Gamma(\alpha_1)\ldots \Gamma(\alpha_K)}x_1^{\alpha_1-1} x_2^{\alpha_2-1}\ldots x_K^{\alpha_K-1} \\[0.7em]
&= \frac{1}{B(\alpha_1,\ldots,\alpha_K)}x_1^{\alpha_1-1} x_2^{\alpha_2-1}\ldots x_K^{\alpha_K-1} \\[0.7em]
&= \frac{1}{B(\valpha)}\prod_{k=1}^{K} x_k^{\alpha_k-1}
\end{align}
ただし,ベータ関数の定義を用いました。
ガンマ分布に従う確率変数の変数変換
ベータ分布を同時確率密度関数で導入したときと同様に,ディリクレ分布を求めてみましょう。$k=1,\ldots,K$に対し,$X_k$は独立かつ
X_k &\sim \Ga(a_k, b)
\end{align}
とします。いま,
Y_k &= \frac{X_k}{\sum_{l=1}^{K} X_l}
\end{align}
とするとき,$Y_1, \ldots, Y_{K-1}$の同時確率密度関数$f(y_1, \ldots, y_{K-1})$がディリクレ分布の確率密度関数と等価になることが知られています。なぜ$y_{K-1}$までの$K-1$個の同時確率分布なのかというと,以前の議論でもあったように,$Y_k$の定義から$\sum_{k=1}^{K}Y_k=1$が成り立ち,独立な変数は$K-1$個になるからです。
まず,$Y_k$の定義通り以下を考えます。
y_k &=\frac{x_k}{\sum_{l=1}^{K} x_l}
\end{align}
これらの逆変換は,以下のようになります。
x_k &= y_k \sum_{l=1}^{K} x_l = y_k z
\end{align}
ただし,見やすさのため,
z &= \sum_{l=1}^{K} x_l
\end{align}
と置きました。次に,ヤコビアンを計算します。
J &=
\abs \begin{vmatrix}
\partial x_1 / \partial y_1 & \ldots & \partial x_1 / \partial y_{K-1} & \partial x_1 / \partial z \\
\vdots & \ddots & \vdots & \vdots \\
\partial x_{K-1} / \partial y_1 & \ldots & \partial x_{K-1} / \partial y_{K-1} & \partial x_{K-1} / \partial z \\
\partial x_{K} / \partial y_1 & \ldots & \partial x_{K} / \partial y_{K-1} & \partial x_{K} / \partial z \
\end{vmatrix} \\[0.7em]
&=
\abs \begin{vmatrix}
z & \ldots & 0 & y_1 \\
\vdots & \ddots & \vdots & \vdots \\
0 & \ldots & z & y_{K-1} \\
-z & \ldots & -z & y_{K} \\
\end{vmatrix}\label{1}\\[0.7em]
&=
\abs \begin{vmatrix}
z & \ldots & 0 & y_1 \\
\vdots & \ddots & \vdots & \vdots \\
0 & \ldots & z & y_{K-1} \\
0 & \ldots & 0 & 1 \\
\end{vmatrix}\label{2}\\[0.7em]
&= z^{K-1}\label{3}
\end{align}
ただし,$|\cdot|$は行列式,$\abs$は絶対値を表します。式($\ref{1}$)から式($\ref{2}$)は,第一行から第$K-1$行を第$K$行に加えて$\sum_k y_k=1$を利用しました。式($\ref{2}$)から式($\ref{3}$)は,上三角行列の行列式が対角成分の積で表されることを利用し,$x_k \geq 0$より$z \geq 0$であることから絶対値を外しました。
$y_1,\ldots, y_{n-1}$の同時分布$f(y_1,\ldots, y_{n-1})$を求めます。これは,$y_1,\ldots, y_{n-1},z$の同時分布$f(y_1,\ldots, y_{n-1},z)$の$z$に関する周辺分布を求めればよいです。計算簡略化のため,正規化定数を除いた部分のみに注目していきます。確率変数の変数変換より,ヤコビアンが$z^{K-1}$であることに注目すると,以下のように周辺分布を計算することができます。
f(y_1,\ldots, y_{n-1})
&= \int_0^{\infty} f(y_1,\ldots, y_{n-1}, z) dz\\[0.7em]
&\propto \int_0^{\infty} \prod_{k=1}^{K} \left\{ \left(y_k z\right)^{a_k-1}e^{-y_k z} \right\} z^{K-1}dz\\[0.7em]
&= \left( \prod_{k=1}^{K}y_k^{a_k-1} \right) \cdot \int_{0}^{\infty} \left\{ z^{\sum_{k=1}^{K} a_k - K}e^{-\left(\sum_{k=1}^{K} y_k\right) z} \right\} z^{K-1} dz \\[0.7em]
&= \left( \prod_{k=1}^{K}y_k^{a_k-1} \right)
\cdot
\int_{0}^{\infty} z^{\sum_{k=1}^{K} a_k - 1} e^{-z} dz \label{4}\\[0.7em]
&\propto \prod_{k=1}^{K}y_k^{a_k-1} \label{5}
\end{align}
ただし,式($\ref{4}$)から式($\ref{5}$)は,ガンマ分布の確率密度関数の形をしていることから,積分は定数になることを利用しました。式($\ref{5}$)は,$y_1,\ldots, y_{n-1}$の同時分布$f(y_1,\ldots, y_{n-1})$がディリクレ分布の形をした確率密度関数となっていることを示しています。正規化定数は「多項分布の共役事前分布」で計算したときと同様に導出することができます。
モーメント母関数
通常,モーメント母関数はモーメント母関数の定義に従って計算していきます。しかし,ベータ分布同様,ディリクレ分布のモーメント母関数は複雑なため,あまり利用されません。
平均・分散
連続分布の平均と分散を求めるためには,モーメント母関数の性質を利用します。しかし,ベータ分布のモーメント母関数は複雑な形をしているため,ここではベータ分布と同様に平均と分散の定義に従って愚直に計算していきます。まず,原点周りの一次モーメント,すなわち期待値を求めます。
E[X_k] &=
C\int_{0}^{\infty} p_1^{x_1-1} \ldots p_k^{x_k}\ldots p_n^{x_n-1} dp_1\ldots dp_{n-1}\\[0.7em]
&= C\cdot\frac{\Gamma(x_1)\ldots\Gamma(x_k+1)\ldots \Gamma(x_n)}{\Gamma(x_1+\ldots+x_n+1)} \\[0.7em]
&= \frac{x_k}{(x_1+\ldots+x_n)}\cdot C \cdot\frac{\Gamma(x_1)\ldots\Gamma(x_k)\ldots \Gamma(x_n)}{\Gamma(x_1+\ldots+x_n)} \\[0.7em]
&= \frac{x_k}{(x_1+\ldots+x_n)}
\end{align}
ただし,$C$はディリクレ分布の正規化定数を表します。次に,原点周りの二次モーメントを求めます。
E[X_k^2] &=
C\int_{0}^{\infty} p_1^{x_1-1} \ldots p_k^{x_k+1}\ldots p_n^{x_n-1} dp_1\ldots dp_{n-1}\\[0.7em]
&= C\cdot\frac{\Gamma(x_1)\ldots\Gamma(x_k+2)\ldots \Gamma(x_n)}{\Gamma(x_1+\ldots+x_n+2)} \\[0.7em]
&= \frac{(x_k+1)x_k}{(x_1+\ldots+x_n+1)(x_1+\ldots+x_n)}\cdot C \cdot\frac{\Gamma(x_1)\ldots\Gamma(x_k)\ldots \Gamma(x_n)}{\Gamma(x_1+\ldots+x_n)} \\[0.7em]
&= \frac{(x_k+1)x_k}{(x_1+\ldots+x_n+1)(x_1+\ldots+x_n)}
\end{align}
最後に,原点周りの一次モーメントと原点周りのの二次モーメントから分散を求めます。
V[X_k] &=
E[X_k^2]-E[X_k]^2 \\[0.7em]
&=\left\{\frac{(x_k+1)x_k}{(x_1+\ldots+x_n+1)(x_1+\ldots+x_n)}\right\}
+ \left\{ \frac{x_k}{(x_1+\ldots+x_n)}\right\}^2 \\[0.7em]
&= \frac{x_k(x_1+\ldots+x_{k-1}+x_{k+1}+\ldots+x_n)}{(x_1+\ldots+x_n+1)(x_1+\ldots+x_n)^2} \\[0.7em]
&= \frac{x_k(\sum_l x_l - x_k)}{(\sum_l x_l + 1)(\sum_l x_l)^2}
\end{align}
再生性
再生性を示すためには,再生性を示したい分布に従う独立な二つの確率変数を考え,その和のモーメント母関数を計算したときに,パラメータが和の形になっていることを示します。ベータ分布同様,ディリクレ分布のモーメント母関数は複雑な形をしており,積をとっても同じ形が出現したいため再生性を持ちません。
ロードマップ
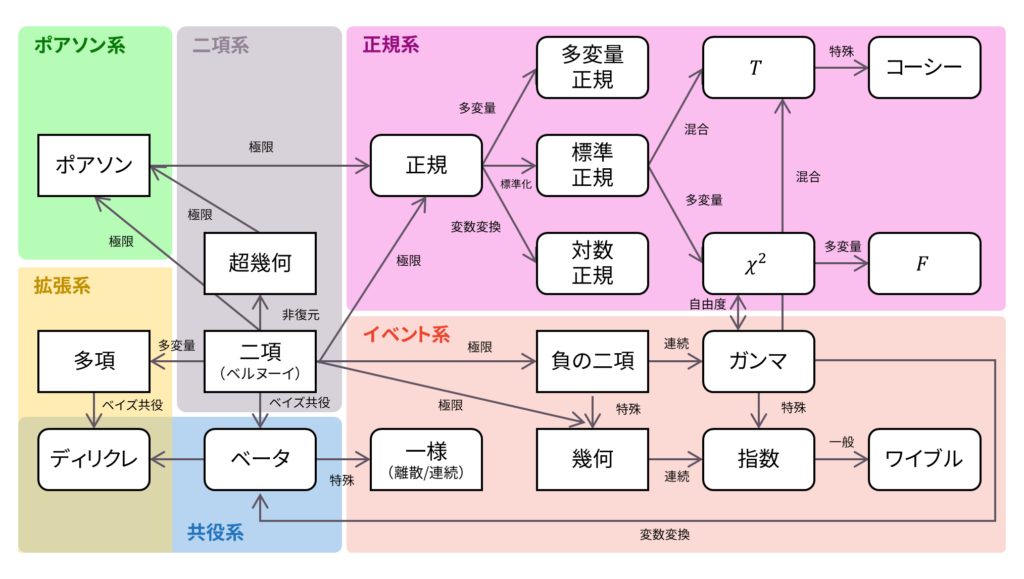
さて,ロードマップに戻りましょう。 ディリクレ分布は,ベータ分布の多変量拡張,すなわち多項分布の共役事前分布として導入されました。ベータ分布同様,ガンマ関数に従う確率変数の変数変換を用いて導入することもできました。以下の内容も参考になるでしょう。
参考文献
本稿の執筆にあたり参考にした文献は,以下でリストアップしております。


コメント