本記事は「これなら分かる!はじめての数理統計学」シリーズに含まれます。
不適切な内容があれば,記事下のコメント欄またはお問い合わせフォームよりご連絡下さい。
カイ二乗分布
f_{X}(x) &= \frac{x^{n/2-1}e^{-x/2}}{2^{n/2}\Gamma\left( n/2 \right)} \\[0.7em]
M_{X}(t) &= \left( \frac{1}{1-2t} \right)^{n/2} \\[0.7em]
E[X] &= n \\[0.7em]
V[X] &= 2n
\end{align}
ただし,$\Gamma(\cdot)$はガンマ関数を表す。
\Gamma(n) &= \int_0^{\infty}t^{n-1}e^{-t}dt
\end{align}
$Y_1,\ldots,Y_n$が独立に$N(0,1)$に従っているとします。このとき,
X &= Y_1^2 + \cdots + Y_n^2
\end{align}
が従う分布を自由度$n$のカイ二乗分布($\chi^2$分布)と呼び,
\chi^2(n)
\end{align}
と表します。カイ二乗分布に従う確率分布$X$に対し,実現値は
x \in \bbR_{+}
\end{align}
であり,モーメント母関数の変数は$t < 1/2$とします。カイ二乗分布は再生性を持ち,ロードマップ中では標準正規分布の多変量化に相当します。同時に,カイ二乗分布はガンマ分布の特殊な場合にも相当します。
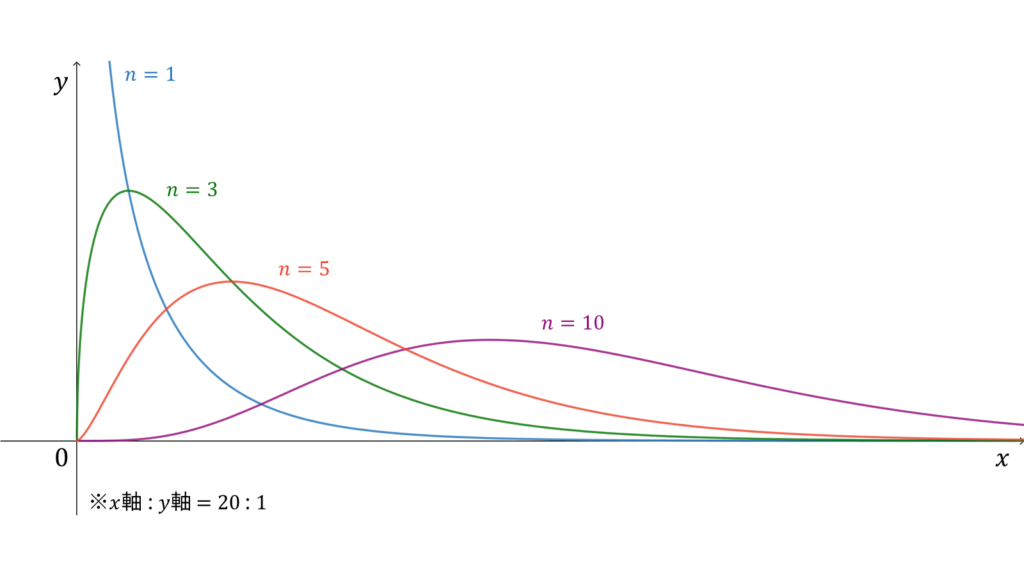
確率密度関数
カイ二乗分布は理論値とのズレに関する統計検定でよく利用され,確率密度関数はガンマ分布の特殊な場合に相当します。定義としては,それぞれ独立に標準正規分布$N(0,1)$に従う$X_1, \ldots, X_n$に対して,二乗和である
Y &= X_1^2 + \cdots + X_n^2 \label{二乗和}
\end{align}
が従う分布を自由度$n$のカイ二乗分布と呼びます。確率密度関数を導出しましょう。
方針としては,まずは自由度$1$のカイ二乗分布の確率密度関数を導出し,それがガンマ分布と等しくなることを示します。次に,ガンマ分布の再生性を利用して自由度$n$のカイ二乗分布の確率密度関数を求めていきたいと思います。改めて,
X &\sim N(0,1) \\[0.7em]
Y &= X^2 \label{Y}
\end{align}
と置きます。式($\ref{Y}$)より$Y\geq 0$であることに注意しましょう。$Y$から$X$を一意に定めることはできず,逆変換は存在しませんので,変数変換の定理を利用することはできません。そこで,今回は累積分布関数を微分することで確率密度関数を求めてみましょう。いま,累積分布関数は
P(X^2 \leq y)=P(-\sqrt{y}\leq X \leq \sqrt{y})
\end{align}
ですので,以下のようにカイ二乗分布の確率密度関数$g(y)$を計算することができます。ただし,標準正規分布の確率密度関数を$f$,原始関数の一つを$F$と書きます。
g(y) &= \frac{d}{dy} P(-\sqrt{y}\leq X \leq \sqrt{y}) \\[0.7em]
&= \frac{d}{dy} \int_{-\sqrt{y}}^{\sqrt{y}} f(x)dx \\[0.7em]
&= \frac{d}{dy} \left\{ F(\sqrt{y}) - F(-\sqrt{y}) \right\} \\[0.7em]
&= \frac{1}{2\sqrt{y}}f(\sqrt{y}) + \frac{1}{2\sqrt{y}}f(-\sqrt{y}) \label{1}\\[0.7em]
&= \frac{1}{2\sqrt{y}}f(\sqrt{y}) + \frac{1}{2\sqrt{y}}f(\sqrt{y}) \label{2}\\[0.7em]
&= \frac{1}{\sqrt{y}}f(\sqrt{y}) \\[0.7em]
&= \frac{1}{2^{1/2}\sqrt{\pi}}y^{-1/2}e^{-y/2}\label{3} \\[0.7em]
&= \frac{1}{2^{1/2}\Gamma(1/2)}y^{1/2-1}e^{-y/2} \label{4} \\[0.7em]
&= \mathrm{Ga}\left(\frac{1}{2}, \frac{1}{2}\right)
\end{alignat}
ただし,式($\ref{1}$)から式($\ref{2}$)は標準正規分布の確率密度関数が奇関数であることを利用し,式($\ref{3}$)から式($\ref{4}$)は
\sqrt{\pi} &= \Gamma\left(\frac{1}{2}\right)
\end{align}
であることを利用しました。したがって,自由度$1$のカイ二乗分布は$\mathrm{Ga}(1/2, 1/2)$と等しくなることが分かりました。ここで,ガンマ分布の再生性より,二乗和($\ref{二乗和}$)は$\mathrm{Ga}(n/2, 1/2)$に従います。つまり,自由度$n$のカイ二乗分布と$\mathrm{Ga}(n/2, 1/2)$は等価ということです。数学的な表記の厳密さを無視すると,以下のことが分かりました。
\chi^2(n) &= \mathrm{Ga}\left( \frac{n}{2}, \frac{1}{2} \right)
\end{align}
これが「カイ二乗分布がガンマ分布の特殊な場合に相当する」とされる所以です。ガンマ分布の確率密度関数より,カイ二乗分布の確率密度関数は以下のようになります。
f(x) &= \frac{1}{2^{n/2}\Gamma\left(n/2\right)}
x^{n/2-1}e^{-x/2}
\end{align}
ただし,$x\geq 0$です。
モーメント母関数
モーメント母関数の定義に従って計算していきます。
M_{X}(t) &= \int_0^{\infty} e^{tx} \frac{x^{n/2-1} e^{-x/2}}{2^{n/2}\Gamma(n/2)} dx\\[0.7em]
&= \int_0^{\infty} \frac{x^{n/2-1} e^{-1/2\cdot(1 - 2t)x}}{2^{n/2}\Gamma(n/2)} dx
\end{align}
ここで,変数変換を用いてカイ二乗分布の確率密度関数の形を再出現させて「確率密度関数を定義域全体で積分したら$1$になる」ことを利用しましょう。
-\frac{1}{2}\left( 1-2t \right) x &= - \frac{y}{2}
\end{align}
したがって,モーメント母関数は以下のようになります。
M_{X}(t) &= \int_0^{\infty} \frac{(1 - 2t)^{-n/2+1} y^{n/2-1} e^{-y/2}}{2^{n/2}\Gamma(n/2)} (1 - 2t)^{-1} dy \\[0.7em]
&= (1 - 2t)^{-n/2} \int_0^{\infty} \frac{y^{n/2-1} e^{-y/2}}{2^{n/2}\Gamma(n/2)} dy\\[0.7em]
&= (1 - 2t)^{-n/2}
\end{align}
平均・分散
連続分布の平均と分散を求めるためには,モーメント母関数の性質を利用します。まず,一次モーメント,すなわち期待値を求めます。
E[X] &= \left.M^{\prime}_{X}(t) \right|_{t=0} \\[0.7em]
&= \left. n(1-2t)^{-n/2-1} \right|_{t=0} \\[0.7em]
&= n
\end{align}
続いて,二次モーメントを求めます。
E[X^2] &= \left.M^{\prime\prime}_{X}(t) \right|_{t=0} \\[0.7em]
&= \left. n(n + 2)(1-2t)^{-n/2-2} \right|_{t=0} \\[0.7em]
&= n(n+2)
\end{align}
最後に,一次モーメントと二次モーメントから分散を求めます。
V[X] &= E[X^2] - E[X]^2 \\[0.7em]
&= n(n+2)-n^2\\[0.7em]
&= 2n
\end{align}
再生性
再生性を示すためには,再生性を示したい分布に従う独立な二つの確率変数を考え,その和のモーメント母関数を計算したときに,パラメータが和の形になっていることを示します。いま,二つの独立な確率変数
X &\sim \chi^2(n) \\[0.7em]
Y &\sim \chi^2(m)
\end{align}
を考えます。このとき,$X+Y$のモーメント母関数を考えます。
M_{X+Y}(t) &= M_{X}(t) \cdot M_{Y}(t) \\[0.7em]
&= (1 - 2t)^{-n/2} \cdot (1 - 2t)^{-m/2} \\[0.7em]
&= (1 - 2t)^{-(n + m)/2}
\end{align}
これは,$X+Y$のモーメント母関数が自由度$n + m$のカイ二乗分布のモーメント母関数であることを示しています。つまり,
X_1+X_2\sim \chi^2(n + m)
\end{align}
であり,カイ二乗分布の再生性を示しています。
ロードマップ
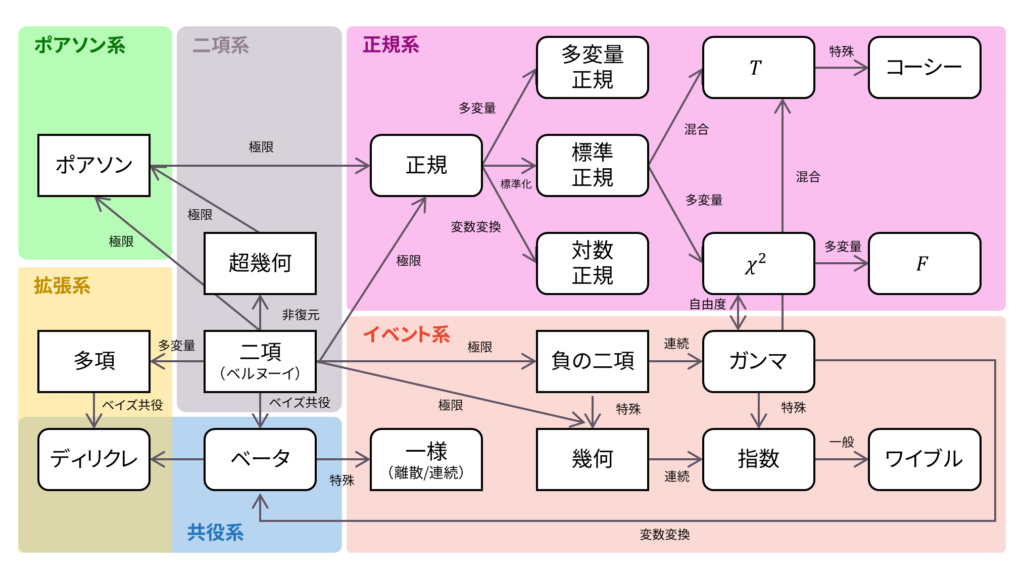
さて,ロードマップに戻りましょう。 カイ二乗分布は,標準正規分布に従う確率変数の二乗和として導入されました。また,その導出過程でカイ二乗分布がガンマ分布の特殊な場合であることも確認しました。さらに,モーメント母関数がシンプルな形をしており,再生性を持つことも確認しました。以下の内容も参考になるでしょう。
参考文献
本稿の執筆にあたり参考にした文献は,以下でリストアップしております。


コメント