本記事は「これなら分かる!はじめての数理統計学」シリーズに含まれます。
不適切な内容があれば,記事下のコメント欄またはお問い合わせフォームよりご連絡下さい。
ベルヌーイ分布
f_{X}(x) &= p^x(1-p)^{1-x} \\[0.7em]
G_{X}(s) &= ps + 1-p \\[0.7em]
E[X] &= p \\[0.7em]
V[X] &= p(1-p)
\end{align}
取り得る結果が成功・失敗の$2$つである試行の結果を表す確率分布をベルヌーイ分布と呼びます。成功する確率を$p \in (0,1)$とおくと,ベルヌーイ分布は以下のように表されます。
\mathrm{Bernoulli}(p)
\end{align}
ベルヌーイ分布に従う確率変数$X$に対し,実現値は
x \in \{0, 1\}
\end{align}
であり,$0$が失敗,$1$が成功を表しているものとします。 また,確率母関数の変数は$|s|\leq 1$とします。ベルヌーイ分布は再生性を持ち,ロードマップ中では二項分布において試行回数が$1$回という特殊な場合に相当します。
確率質量関数
一回のコイントスに関して表が出る確率を$p$とします。確率変数は$1$のとき表が出たという事象を,$0$のとき裏が出た事象を表します。このような状況を設定すれば,ベルヌーイ分布の確率質量関数は自然に導かれます。
f_{X}(x) &= p^x(1-p)^{1-x}
\end{align}
確率母関数
確率母関数の定義に従って計算していきます。
G_{X}(s) &= E[s^x] \\[0.7em]
&= \sum_{x=0}^{1}P(X=x)\cdot s^x \\[0.7em]
&= \sum_{x=0}^{1} (ps)^x(1-p)^{1-x} \\[0.7em]
&= 1-p+ps \\[0.7em]
&= ps+1-p
\end{align}
平均・分散
離散分布の平均と分散を求めるためには,確率母関数の性質を利用します。まず,確率母関数の一階微分から$E[X]$を求めます。
E[X] &= \left.\frac{d G_{X}(s)}{d s}\right|_{s=1} \\[0.7em]
&= p
\end{align}
続いて,確率母関数の二階微分から$E[X(X-1)]$を求めます。
E[X(X-1)] &= \left.\frac{d^2 G_{X}(s)}{d s^2}\right|_{s=1} \\[0.7em]
&= 0
\end{align}
最後に,分散の定義から分散を求めます。
V[X] &= E[X^2]-E[X]^2 \\[0.7em]
&= E[X(X-1)] + E[X]-E[X]^2 \\[0.7em]
&= 0 + p-p^2 \\[0.7em]
&= p(1-p)
\end{align}
再生性
再生性を示すためには,再生性を示したい分布に従う独立な二つの確率変数を考え,その和の確率母関数を計算したときに,パラメータが和の形になっていることを示します。しかし,ベルヌーイ分布には再生性がないことはすぐ分かります。なぜなら,ベルヌーイ分布に従う2つの確率変数の和は二項分布に従うからです。確率変数の和が別の確率分布に従うときは,再生性をもつとはいいません。
ロードマップ
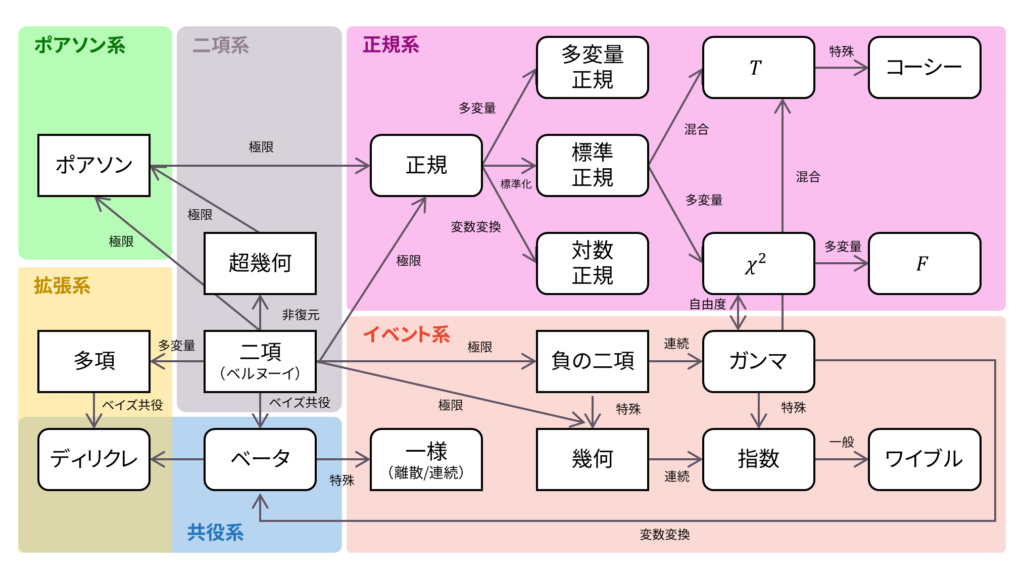
さて,ロードマップに戻りましょう。 ベルヌーイ分布は二項分布と同じ場所に属しています。これは,二項分布において各試行はベルヌーイ分布に従うからです。ロードマップは二項分布を中心に広がっていきますから,最も基本的な分布としてベルヌーイ分布をおさえておきましょう。以下の内容も参考になるでしょう。
参考文献
本稿の執筆にあたり参考にした文献は,以下でリストアップしております。


コメント