【徹底解説】対数正規分布とは

2023年10月28日

本記事は「これなら分かる！はじめての数理統計学」シリーズに含まれます。

不適切な内容があれば，記事下のコメント欄またはお問い合わせフォームよりご連絡下さい。

対数正規分布

\begin{align}
f_{X}(x) &= \frac{1}{\sqrt{2\pi\sigma^2}}\frac{1}{x}\exp\left\{ -\frac{1}{2\sigma^2} (\log x-\mu)^2 \right\} \\[0.7em]
E[X] &= e^{\mu + \sigma^2/2} \\[0.7em]
V[X] &= e^{2\mu + \sigma^2}\left( e^{\sigma^2}-1 \right)
\end{align}

正規分布$\N (\mu, \sigma^2)$に従う確率変数$Y$対して，

\begin{align}
X &= e^{Y}
\end{align}

が従う分布を対数正規分布と呼びます。$\log X$が正規分布に従うことが名前の由来になっています。対数正規分布に従う確率変数$X$に対し，実現値は

\begin{align}
x \in \bbR_{+}
\end{align}

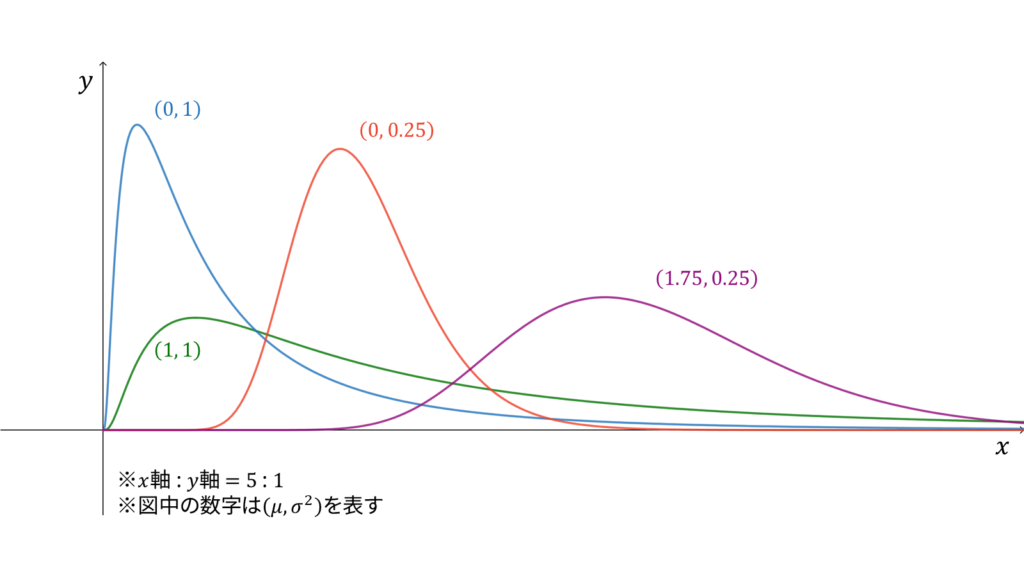
であり，モーメント母関数は存在しません。対数正規分布は再生性を持たず，ロードマップ中では正規分布からの変数変換に相当します。注意点として，確率密度関数中の$\mu$と$\sigma^2$は正規分布とは異なり，それぞれ平均と分散には対応しません。

確率密度関数

正規分布$\N (\mu, \sigma)$に従う確率変数$Y$に対し，

\begin{align}
X &= e^Y \\[0.7em]
Y &= \log X
\end{align}

の従う分布が対数正規分布になります。実際に計算していきましょう。

\begin{align}
\frac{dy}{dx} &= \frac{1}{x}
\end{align}

を踏まえれば，正規分布の確率密度関数を$f(x)$，対数正規分布の確率密度関数を$g(x)$とすると，以下が成り立ちます。

\begin{align}
f(x) dx &= g(y) dy \\[0.7em]
f(x) &= g(y) \frac{dy}{dx} \\[0.7em]
&= \frac{g(\log x)}{x}
\end{align}

従って，$f(x)$は以下のように表されます。

\begin{align}
f(x) &= \frac{1}{\sqrt{2\pi \sigma^2}x} \exp\left\{-\frac{(\log x - \mu)^2}{2 \sigma^2}\right\}
\end{align}

モーメント母関数

対数正規分布のモーメント母関数が存在しないことを確認します。モーメント母関数の定義に従って計算していきますが，$x > 0$に注意してください。

\begin{align}
M_{X}(t) &= E[e^{tX}] \\[0.7em]
&= \int_{0}^{\infty} \frac{1}{\sqrt{2\pi \sigma^2}x} \exp\left\{ -\frac{(\log x-\mu)^2}{2\sigma^2} + tx \right\} dx
\end{align}

さて，$x \rightarrow \infty$のときに右辺が発散することを示します。被積分関数のうち，$x$に関わりのない定数項を除いたものを$h$としたときに，その対数$\log h$は以下のようになります。

\begin{align}
\log h &= \log \frac{\exp\left\{ -\left( \log x \right)^2 + \log x + tx \right\}}{x} \\[0.7em]
&=-\left( \log x \right)^2 + \log x + (t-1)x
\end{align}

ここで，$x \geq \log x + 1$を利用して$h$を下からおさえます。分かりやすさのため，途中で$\log x = z$とおきます。

\begin{align}
h &\geq -\left( \log x \right)^2 + \log x + (t-1)(\log x + 1) \\[0.7em]
&= -z^2 + tz + (t-1)
\end{align}

右辺は上に凸の二次関数ですので，$z \rightarrow \infty$のとき発散します。$\log$関数を取る前後で増減が変わらないことから，$x \rightarrow \infty $のときも$h$は発散することが分かります。したがって，モーメント母関数の被積分関数が$ x \rightarrow \infty $で発散することが示せたため，モーメント母関数が存在しないことが確認できました。

平均・分散

対数正規分布の平均と分散は，正規分布のモーメント母関数を利用して美しく求めることができます。正規分布$\N (\mu, \sigma)$に従う確率変数$Y$に対し，$e^Y$が従う分布が対数正規分布でした。$Y$のモーメント母関数は以下の通りです。

\begin{align}
M_{Y}(t) &= E[e^{tY}] \\[0.7em]
&= \exp\left(\mu t + \frac{\sigma^2 t^2}{2} \right)
\end{align}

ここで，モーメント母関数が$t$の関数であることから，$Y$のモーメント母関数において$Y$を$\log X$に置き換えられることを利用します。

\begin{align}
E[e^{t\log X}] &= E[X^t] \\[0.7em]
&= \exp\left(\mu t + \frac{\sigma^2 t^2}{2} \right) \\[0.7em]
\end{align}

なんと，対数正規分布の$t$次モーメントが正規分布のモーメント母関数に対応していることが分かりました。つまり，$M_{Y}(n)$が$X$の$n$次モーメントになります。ですので，平均と分散は正規分布のモーメント母関数を利用して簡単に求められます。

\begin{align}
E[X] &= M_{Y}(1) \\[0.7em]
&= \exp\left(\mu + \frac{\sigma^2}{2} \right) \\[0.7em]
V[X] &= M_{Y}(2)-M_{Y}(1)^2 \\[0.7em]
&= \exp\left(2 \mu + 2 \sigma^2 \right) - \exp\left(2 \mu + \sigma^2 \right) \\[0.7em]
&= \exp\left(2 \mu + \sigma^2 \right) \left\{\exp\left( \sigma^2 \right)- 1 \right\}
\end{align}

再生性

再生性を示すためには，再生性を示したい分布に従う独立な二つの確率変数を考え，その和のモーメント母関数を計算したときに，パラメータが和の形になっていることを示します。モーメント母関数が存在しないことからも分かる通り，対数正規分布は再生性を持ちません。一方で，確率変数の積に対して対数正規分布は再生性を持ちます。正規分布の再生性から，

\begin{align}
S\sim \N (\mu_s, \sigma^2_s) \\[0.7em]
T\sim \N (\mu_t, \sigma^2_t)
\end{align}

に対して

\begin{align}
S+T &\sim \N (\mu_s+\mu_t, \sigma^2_s + \sigma^2_t)
\end{align}

が成り立つことを利用すると，

\begin{align}
\log X\sim \N (\mu_x, \sigma^2_x) \\[0.7em]
\log Y\sim \N (\mu_y, \sigma^2_y)
\end{align}

に対して，

\begin{align}
\log X + \log Y &= \log XY \\[0.7em]
&\sim \N (\mu_x+\mu_y, \sigma^2_x+\sigma^2_y) \label{logX+logY}
\end{align}

が成り立つことが分かります。$\log X$が正規分布に従うとき，$X$の従う分布が対数正規分布であることに注意すると，式($\ref{logX+logY}$)は対数正規分布の積に関する再生性を表しています。

ロードマップ

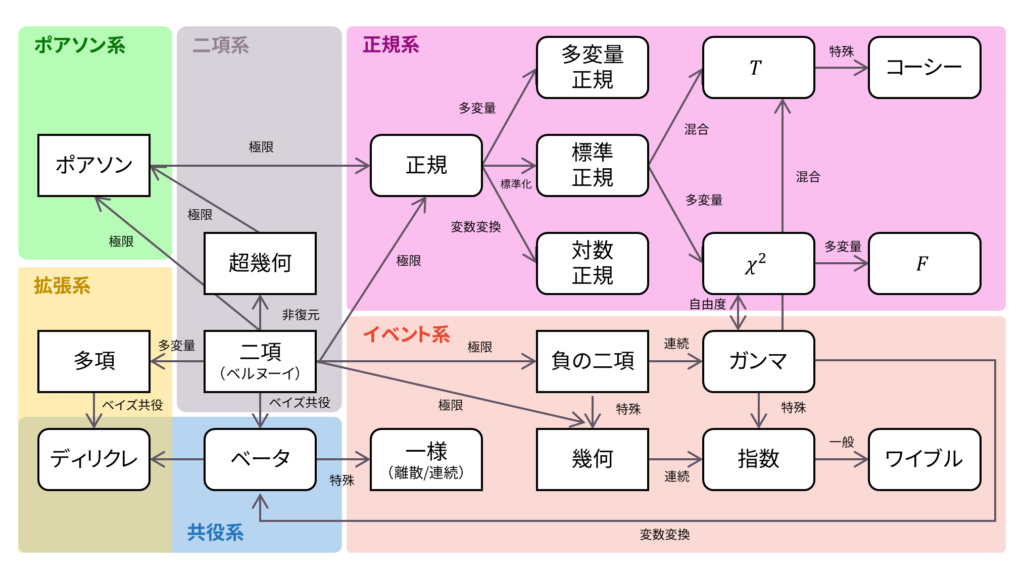
さて，ロードマップに戻りましょう。対数正規分布は，$\log X$が正規分布に従うときに$X$が従う分布でした。すなわち，対数正規分布は正規分布に従う確率変数の変数変換によって導出される確率分布です。以下の内容も参考になるでしょう。

正規分布とは

参考文献

本稿の執筆にあたり参考にした文献は，以下でリストアップしております。

参考文献リストへ

シェアはこちらからお願いします！