【徹底解説】負の二項分布とは

2022年6月23日

本記事は「これなら分かる！はじめての数理統計学」シリーズに含まれます。

不適切な内容があれば，記事下のコメント欄またはお問い合わせフォームよりご連絡下さい。

負の二項分布

\begin{align}
f_{X}(x) &= {}_{x+r-1} C_{x}\;p^r (1-p)^{x} \\[0.7em]
G_{X}(s) &= \left\{ \frac{p}{1-(1-p)s} \right\}^r \\[0.7em]
E[X] &= r\frac{1-p}{p} \\[0.7em]
V[X] &= r \frac{1-p}{p^2}
\end{align}

無限に続くベルヌーイ試行において，$r$回成功するまでの失敗の回数$X$は負の二項分布

\begin{align}
\NB (r, p)
\end{align}

に従います。ただし，$r \in \bbN$，$p \in [0, 1]$とします。負の二項分布に従う確率変数$X$に対し，実現値は

\begin{align}
x_k \in \{0, 1, \ldots \}
\end{align}

であり，確率母関数の変数は$|s_k|\leq 1$とします。負の二項分布は再生性を持ち，ロードマップ中では負の二項分布は二項分布の極限に相当します。なお，負の二項分布はポアソン分布の混合分布としても定義されます。

確率密度関数

負の二項分布は「$r$回表が出るまでの失敗の回数」を確率変数とする確率分布です。この定義から，確率密度関数は自然に導かれます。

\begin{align}
f_{X}(x) &= {}_{x+r-1} C_{x}\;p^r (1-p)^{x}
\end{align}

確率母関数

負の二項分布の確率母関数を求めるには，「$r$回表が出るまでの失敗の回数」を「$1$回表が出るまでの失敗の回数の和」として捉えると簡単です。つまり，幾何分布に従う$r$個の独立な確率変数$X_1,\cdots,X_r$の和$S_r$が負の二項分布に従います。したがって，確率母関数は以下のようになります。

\begin{align}
G_{S_r}(s) &= G_{X_1+\cdots X_r}(s) \\[0.7em]
&= G_{X_1}(s)\cdots G_{X_r}(s)\\[0.7em]
&= \left\{ \frac{p}{1-(1-p)s} \right\}^r
\end{align}

一般的な確率母関数の導出方法もご紹介しておきます。一般二項定理と呼ばれている以下のテイラー級数を利用します。

\begin{align}
(1-t)^{-r} &= \sum_{x=0}^{\infty} \frac{(r)_x}{x!}t^x \label{equation：一般二項定理}
\end{align}

ただし，超幾何分布で導入した記号と同様に，$N$から$n$個分の中途半端な階乗を$(N)_n$と表します。

\begin{align}
(N)_n &= N(N-1)\cdots (N-n+1)
\end{align}

さて，確率母関数の定義通りに計算していきます。

\begin{align}
E[s^x] &= \sum_{x=0}^{\infty} s^x {}_{x+r-1}\C_{x}p^r (1-p)^x\\[0.7em]
&= \sum_{x=0}^{\infty} s^x \frac{(x+r-1)!}{x! (r-1)!}p^r (1-p)^x\\[0.7em]
&= \sum_{x=0}^{\infty} \frac{(x+r-1)!}{x! (r-1)!}p^r \left\{ (1-p)s\right\}^x\\[0.7em]
&= p^r \sum_{x=0}^{\infty} \frac{(r)_x}{x!}\left\{ (1-p)s\right\}^x\\[0.7em]
&= p^r \left\{1 - (1-p)s\right\}^{-r}\\[0.7em]
&= \left\{ \frac{p}{1-(1-p)s} \right\}^r
\end{align}

平均・分散

離散分布の平均と分散を求めるためには，確率母関数の性質を利用します。

\begin{align}
E[S_r] &= E[X_1 + \cdots + X_r]\\[0.7em]
&= E[X_1] + \cdots + E[X_r]\\[0.7em]
&= r\frac{1-p}{p}\\[0.7em]
V[S_r] &= V[X_1 + \cdots + X_r]\\[0.7em]
&= V[X_1] + \cdots + V[X_r]\\[0.7em]
&= r\frac{1-p}{p^2}\\[0.7em]
\end{align}

ただし，分散の計算では$X_1, \ldots, X_r$がそれぞれ互いに独立であることを利用しました。

再生性

再生性を示すためには，再生性を示したい分布に従う独立な二つの確率変数を考え，その和の確率母関数を計算したときに，パラメータが和の形になっていることを示します。

確率母関数の形に注目すると，二項分布の再生性を示したときと全く同様にして再生性を示すことができます。そこで，二項分布と同様の式変形を行えるようにするため，負の二項分布を二項分布の形に変形してみましょう。この操作こそが，負の二項分布が「負の」二項分布と呼ばれている由来です。まずは，負の二項係数の定義を確認しましょう。

\begin{align}
{}_{-r}C_{x} &=\frac{(-r)(-r-1) \cdots\left\{ -r-(x-1)\right\}}{x !} \\[0.7em]
&=(-1)^{x} \frac{r(r+1) \cdots(r+x-1)}{x !} \\[0.7em]
&=(-1)^{x} {}_{x+r-1} C_{x}
\end{align}

二項定理の公式を負の二項定理に利用すると，以下の等式が成り立つことに注意しましょう。

\begin{align}
\sum_{k=0}^{n} {}_{n} C_{k} x^{k} y^{n-k}=(x+y)^{n} \label{equation：二項定理の和}
\end{align}

これらの式を使って確率母関数を計算します。

\begin{align}
E[s^x] &= \sum_{x=0}^{\infty} s^x {}_{x+r-1}C_{x}p^r (1-p)^x\\[0.7em]
&= p^r\sum_{x=0}^{\infty} s^x (-1)^x {}_{-r}C_{x} (1-p)^x\\[0.7em]
&= p^r\sum_{x=0}^{\infty} {}_{-r}C_{x} \left\{ -(1-p)s\right\}^x\\[0.7em]
&= p^r\sum_{x=0}^{\infty} {}_{-r}\mathrm{C}_{x} \left\{ -(1-p)s\right\}^x \cdot (1)^{-r-x}\\[0.7em]
&= p^r \left\{ 1-(1-p)s \right\}^{-r} \quad (\because \text{式(\ref{equation：二項定理の和})より})\\[0.7em]
&= \left\{ \frac{p}{1-(1-p)s} \right\}^r
\end{align}

ロードマップ

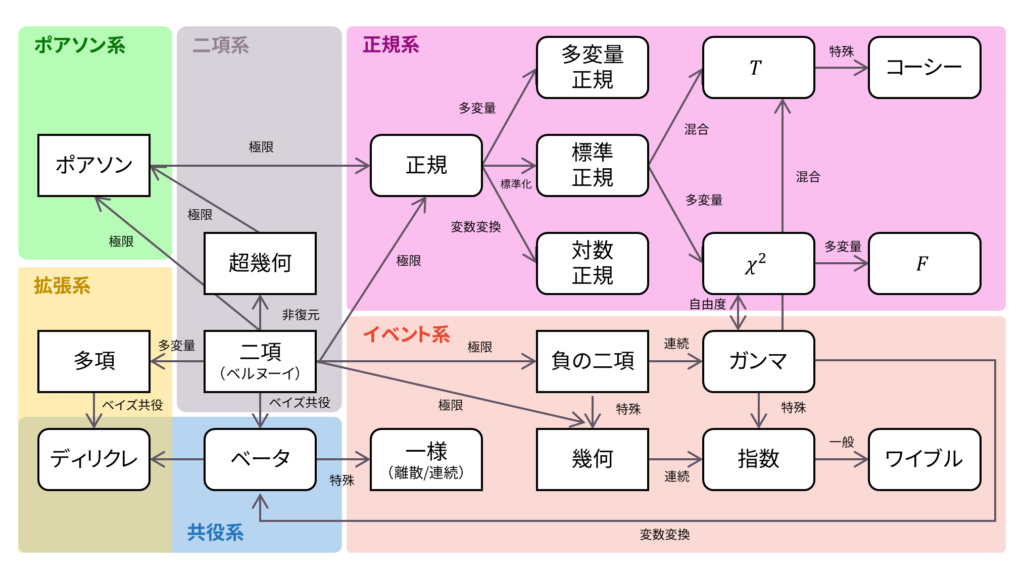
さて，ロードマップに戻りましょう。負の二項定理は二項定理を一般に拡張したテイラー級数を利用して母関数が求められました。また，幾何分布に従う確率変数の和としても定義できました。逆に言えば，負の二項分布において，$r=1$という特殊な場合が幾何分布に相当するということになります。以下の内容も参考になるでしょう。

参考文献

本稿の執筆にあたり参考にした文献は，以下でリストアップしております。

参考文献リストへ

シェアはこちらからお願いします！