本稿では,代表的な微分方程式の解法をお伝えします。
初学者の分かりやすさを優先するため,多少正確でない表現が混在することがあります。もし致命的な間違いがあればご指摘いただけると助かります。
宣伝
線形微分方程式を一瞬で解くことができる「必殺奥義」を解説しています。大学の定期試験や数学検定1級の対策として非常に有効な武器となりますので,ぜひ参考にしてください。
Academaid
【ぶっ壊れ解法】線形微分方程式を瞬殺する必殺奥義 | Academaid
線形微分方程式を一瞬で解くことができる「必殺奥義」である微分演算子法について解説します。本手法は大学の定期試験や数学検定1級の対策として非常に有効な武器となりま...
目次
変数分離形の微分方程式
\begin{align}
\frac{dy}{dx} &= \frac{y}{x(y+1)} \\[0.7em]
\frac{dy}{dx} &= (x + y)^2
\end{align}
\frac{dy}{dx} &= \frac{y}{x(y+1)} \\[0.7em]
\frac{dy}{dx} &= (x + y)^2
\end{align}
同次形の微分方程式
\begin{align}
(7x + 4y)\frac{dy}{dx} &= -8x -5y
\end{align}
(7x + 4y)\frac{dy}{dx} &= -8x -5y
\end{align}
有理関数型の微分方程式
\begin{align}
\frac{dy}{dx} &= f\left(\frac{ax+by+c}{px+qy+r}\right)
\end{align}
\frac{dy}{dx} &= f\left(\frac{ax+by+c}{px+qy+r}\right)
\end{align}
1階線形微分方程式
\begin{align}
(x^2 + a^2)y^{\prime} + xy &= 1
\end{align}
(x^2 + a^2)y^{\prime} + xy &= 1
\end{align}
ベルヌーイの微分方程式
\begin{align}
x\frac{dy}{dx} + y &= y^2 \log x
\end{align}
x\frac{dy}{dx} + y &= y^2 \log x
\end{align}
完全微分方程式
\begin{align}
(3x^2 + \cos y) dx &= (2y - x\sin y) dy \\[0.7em]
(y + \log x)dx + x\log x dy &= 0
\end{align}
(3x^2 + \cos y) dx &= (2y - x\sin y) dy \\[0.7em]
(y + \log x)dx + x\log x dy &= 0
\end{align}
2階同次線形微分方程式
\begin{align}
y^{\prime\prime} + 5y^{\prime} + 4y &= 0 \\[0.7em]
y^{\prime\prime} + 4y^{\prime} + 4y &= 0 \\[0.7em]
y^{\prime\prime} - 2y^{\prime} + 4y &= 0
\end{align}
y^{\prime\prime} + 5y^{\prime} + 4y &= 0 \\[0.7em]
y^{\prime\prime} + 4y^{\prime} + 4y &= 0 \\[0.7em]
y^{\prime\prime} - 2y^{\prime} + 4y &= 0
\end{align}
2階同次線形微分方程式については,下記の徹底解説記事もご参照ください。
Academaid
【ぶっ壊れ解法】線形微分方程式を瞬殺する必殺奥義 | Academaid
線形微分方程式を一瞬で解くことができる「必殺奥義」である微分演算子法について解説します。本手法は大学の定期試験や数学検定1級の対策として非常に有効な武器となりま...
2階非同次線形微分方程式
\begin{align}
y^{\prime\prime} + 5y^{\prime} + 4y &= x^{2}\\[0.7em]
y^{\prime\prime} + 5y^{\prime} + 4y &= \sin x\\[0.7em]
y^{\prime\prime} + 5y^{\prime} + 4y &= e^{x}\\[0.7em]
y^{\prime\prime} + 5y^{\prime} + 4y &= e^{x}x^{2}\\[0.7em]
y^{\prime\prime} + 5y^{\prime} + 4y &= e^{x} \sin x\\[0.7em]
y^{\prime\prime} + 5y^{\prime} &= x^{2}\\[0.7em]
y^{\prime\prime} &= x^{2}\\[0.7em]
y^{\prime\prime} + 5y^{\prime} + 4y &= e^{-x}\\[0.7em]
y^{\prime\prime} + 4y^{\prime} + 4y &= e^{-2x}\\[0.7em]
y^{\prime\prime} + 5y^{\prime} + 4y &= x^{2}e^{-x}\\[0.7em]
y^{\prime\prime} + 4y^{\prime} + 4y &= x^{2}e^{-2x}\\[0.7em]
y^{\prime\prime} + 2y^{\prime} + 4y &= e^{-x} \sin \sqrt{3}x
\end{align}
y^{\prime\prime} + 5y^{\prime} + 4y &= x^{2}\\[0.7em]
y^{\prime\prime} + 5y^{\prime} + 4y &= \sin x\\[0.7em]
y^{\prime\prime} + 5y^{\prime} + 4y &= e^{x}\\[0.7em]
y^{\prime\prime} + 5y^{\prime} + 4y &= e^{x}x^{2}\\[0.7em]
y^{\prime\prime} + 5y^{\prime} + 4y &= e^{x} \sin x\\[0.7em]
y^{\prime\prime} + 5y^{\prime} &= x^{2}\\[0.7em]
y^{\prime\prime} &= x^{2}\\[0.7em]
y^{\prime\prime} + 5y^{\prime} + 4y &= e^{-x}\\[0.7em]
y^{\prime\prime} + 4y^{\prime} + 4y &= e^{-2x}\\[0.7em]
y^{\prime\prime} + 5y^{\prime} + 4y &= x^{2}e^{-x}\\[0.7em]
y^{\prime\prime} + 4y^{\prime} + 4y &= x^{2}e^{-2x}\\[0.7em]
y^{\prime\prime} + 2y^{\prime} + 4y &= e^{-x} \sin \sqrt{3}x
\end{align}
2階非同次線形微分方程式については,下記の徹底解説記事もご参照ください。
Academaid
【ぶっ壊れ解法】線形微分方程式を瞬殺する必殺奥義 | Academaid
線形微分方程式を一瞬で解くことができる「必殺奥義」である微分演算子法について解説します。本手法は大学の定期試験や数学検定1級の対策として非常に有効な武器となりま...
オイラーの微分方程式
\begin{align}
x^2 \frac{d^2 y}{dx^2} - 3x\frac{dy}{dx}+ 4y &= x^2\log x
\end{align}
x^2 \frac{d^2 y}{dx^2} - 3x\frac{dy}{dx}+ 4y &= x^2\log x
\end{align}
クレローの微分方程式
\begin{align}
y &= xy^{\prime} + \left( y^{\prime}\right)^2
\end{align}
y &= xy^{\prime} + \left( y^{\prime}\right)^2
\end{align}
ラグランジュ(ダランベール)の微分方程式
\begin{align}
y &= (y^{\prime}+1)x + \left( y^{\prime}\right)^2
\end{align}
y &= (y^{\prime}+1)x + \left( y^{\prime}\right)^2
\end{align}
リッカチの微分方程式
\begin{align}
y^{\prime}&=e^x-y+e^{-x}y^2
\end{align}
y^{\prime}&=e^x-y+e^{-x}y^2
\end{align}
線形微分方程式の級数解法
\begin{align}
y^{\prime\prime}-\frac{x}{x-1}y^{\prime}+\frac{y}{x-1} &= x-1
\end{align}
y^{\prime\prime}-\frac{x}{x-1}y^{\prime}+\frac{y}{x-1} &= x-1
\end{align}
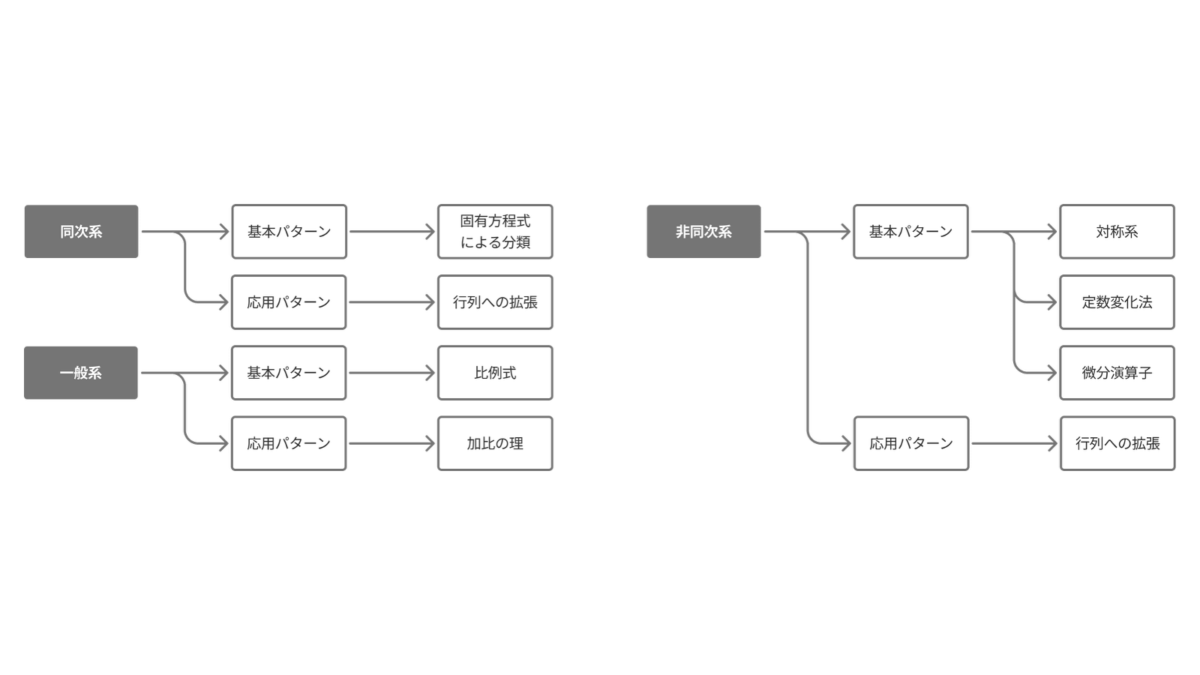
連立微分方程式


コメント