本稿では,代表的な微分方程式の解法をお伝えします。
初学者の分かりやすさを優先するため,多少正確でない表現が混在することがあります。もし致命的な間違いがあればご指摘いただけると助かります。
宣伝
線形微分方程式を一瞬で解くことができる「必殺奥義」を解説しています。大学の定期試験や数学検定1級の対策として非常に有効な武器となりますので,ぜひ参考にしてください。
連立微分方程式
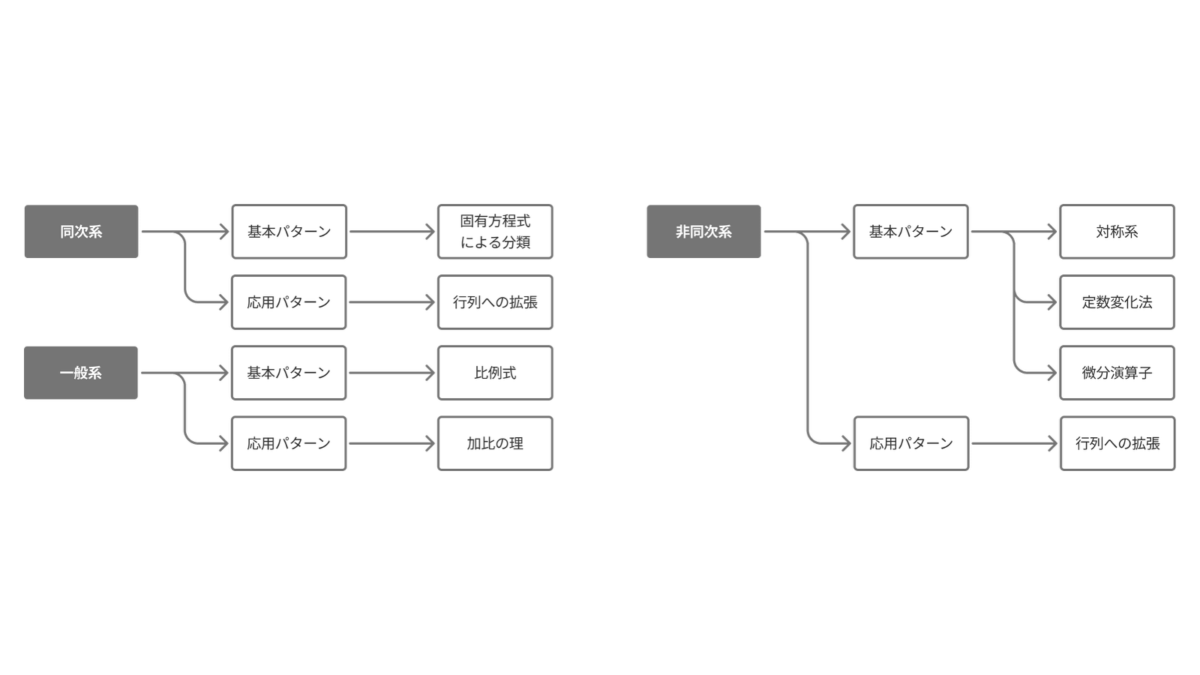
一口に連立微分方程式と言っても様々な種類が存在します。本稿では,連立微分方程式として押さえておくべきパターンを整理し,それぞれの解法をみていきます。
同次系
連立方程式として最も基本的なパターンは,以下の定数係数の連立同次線形微分方程式です。
\begin{cases}
y_{1}^{\prime}(t) = a_{11}y_{1}(t)+a_{12}y_{2}(t)+\cdots+a_{1n}y_{n}(t)\\[0.7em]
y_{2}^{\prime}(t) = a_{21}y_{1}(t)+a_{22}y_{2}(t)+\cdots+a_{2n}y_{n}(t)\\[0.7em]
\quad\vdots\\[0.7em]
y_{n}^{\prime}(t) = a_{n1}y_{1}(t)+a_{n2}y_{2}(t)+\cdots+a_{nn}y_{n}(t)
\end{cases}\label{同次系}
\end{align}
$\vy=(y_{1},y_{2},\ldots,y_{n})$,係数行列を$A$とおくと,式($\ref{同次系}$)は
\frac{d\vy}{dt} &= A\vy
\end{align}
と書くことができます。ここで,線形微分方程式を瞬殺する必殺奥義でお伝えした通り,$n$階線形微分方程式の解は$n$個の一次独立な解の一次結合として表されますので,仮に解が
\vy &= (k_{1}e^{\lambda t},k_{2}e^{\lambda t},\ldots,k_{n}e^{\lambda t})
\equiv \vk e^{\lambda t}
\label{同次系_解の仮定}
\end{align}
という形で表され,線形独立な解の一次結合で表すことができれば,式($\ref{同次系}$)の解として必要十分となります。式($\ref{同次系_解の仮定}$)を式($\ref{同次系}$)に代入すると,
\lambda \vk e^{\lambda t} &= A\vk e^{\lambda t}
\end{align}
となるため,両辺を$e^{\lambda t}\neq 0$で割ると$A\vk=\lambda\vk$という$A$の固有値問題が得られます。すなわち,$\vy(t)$が$\vzero$以外の解を持つためには$\det(A-\lambda I)=0$となりますので,固有方程式を解くことにより式($\ref{同次系}$)の解を得ることができます。固有方程式と線形微分方程式の関係は以下の記事で詳しく解説していますので,本稿では軽く流れだけを見ていきます。
固有方程式が異なる実数解を持つとき
\begin{cases}
x^{\prime}=x-z\\[0.7em]
y^{\prime}=x+2y+z\\[0.7em]
z^{\prime}=2x+2y+3z
\end{cases}
\end{align}
固有方程式は$\lambda=1,2,3$の解を持ち,それぞれの固有ベクトルは
- $\lambda=1$のとき:$(x,y,z)=(e^{t},-e^{t},0)$
- $\lambda=2$のとき:$(x,y,z)=(-2e^{2t},e^{t},2e^{t})$
- $\lambda=3$のとき:$(x,y,z)=(e^{3t},-e^{3t},-2e^{3t})$
となりますので,求める答えは
\begin{cases}
x = c_{1}e^{t}-2c_{2}e^{2t}+c_{3}e^{3t}\\[0.7em]
y = -c_{1}e^{t}+c_{2}e^{2t}-c_{3}e^{3t}\\[0.7em]
z = 2c_{2}e^{2t}-2c_{3}e^{3t}
\end{cases}
\end{align}
となります。
固有方程式が重複する実数解を持つとき
\begin{cases}
x^{\prime}=x-z\\[0.7em]
y^{\prime}=2x+2y+2z\\[0.7em]
z^{\prime}=2x+y+2z
\end{cases}
\end{align}
固有方程式は$\lambda=1,2$ (二重解) の解を持ち,それぞれの固有ベクトルは
- $\lambda=1$のとき:$(x,y,z)=(e^{t},-2e^{t},0)$
- $\lambda=2$のとき:$(x,y,z)=(e^{2t},-2e^{2t},-e^{2t})$
となります。$\lambda=2$は重解ですので,線形微分方程式を瞬殺する必殺奥義で説明している解の置き方に従い,
\begin{cases}
x=(k+t)e^{2t}\\[0.7em]
y=(l-2t)e^{2t}\\[0.7em]
z=(m-t)2^{2t}
\end{cases}
\end{align}
とおいて元の連立微分方程式に代入すると,
\begin{cases}
k+m=-1\\[0.7em]
2k+l=01
\end{cases}
\end{align}
が得られます。答えを単純にするため$k=0$とすれば,$(l,m)=(-1,-1)$となります。ゆえに,
- $\lambda=2$のとき:$(x,y,z)=(te^{2t},-(1+2t)e^{2t},-(1+t)e^{2t})$
も得られます。以上より,求める答えは
\begin{cases}
x = c_{1}e^{t}+(c_{2}+c_{3}t)e^{2t}\\[0.7em]
y = -2c_{1}e^{t}-(2c_{2}+c_{3}(1+2t))e^{2t}\\[0.7em]
z = -(c_{2}+c_{3}(1+t))e^{2t}
\end{cases}
\end{align}
となります。
3重解の場合でも同様の手続きに従います。
よくある誤解
連立でない微分方程式と同様のノリで,係数を全て$c_{1},c_{2},c_{3}$に吸収させて
\begin{cases}
x = c_{1}e^{t}+(c_{2}+c_{3}t)e^{2t}\\[0.7em]
y = c_{1}e^{t}+(c_{2}+c_{3}t)e^{2t}\\[0.7em]
z = (c_{2}+c_{3}t)e^{2t}
\end{cases}
\end{align}
としてはいけません。連立することにより,係数の比に関しても制約条件がありますので,必ず上述のように係数を求めるように注意してください。
固有方程式が複素解をもつとき
\begin{cases}
x^{\prime}=y+z\\[0.7em]
y^{\prime}=-z\\[0.7em]
z^{\prime}=-x+z
\end{cases}
\end{align}
固有方程式は$\lambda=1,\pm i$の解を持ち,それぞれの固有ベクトルは
- $\lambda=1$のとき:$(x,y,z)=(0,e^{t},-e^{t})$
- $\lambda=i$のとき:$(x,y,z)=((1-i)e^{it},ie^{it},e^{it})$
- $\lambda=-i$のとき:$(x,y,z)=((1+i)e^{-it},-ie^{-it},e^{-it})$
となりますので,求める答えは
\begin{cases}
x = c_{2}(1-i)e^{it}+c_{3}(1+i)e^{-it} = c_{2}^{\prime}(\sin t+\cos t)+c_{3}^{\prime}(\sin t-\cos t)\\[0.7em]
y = c_{1}^{\prime}e^{t}+c_{2}ie^{it}-c_{3}ie^{-it} = c_{1}^{\prime}e^{t}-c_{2}^{\prime}\sin t+c_{3}^{\prime}\cos t\\[0.7em]
z = -c_{1}^{\prime}e^{t}+c_{2}e^{it}+c_{3}e^{-it} = -c_{1}^{\prime}e^{t}+c_{2}^{\prime}\cos t+c_{3}^{\prime}\sin t
\end{cases}
\end{align}
となります。ただし,オイラーの公式を利用しました。
非同次系
連立非同次線形微分方程式は,次のような形をしています。
\begin{cases}
y_{1}^{\prime}(t) = a_{11}y_{1}(t)+a_{12}y_{2}(t)+\cdots+a_{1n}y_{n}(t)+f_{1}(t)\\[0.7em]
y_{2}^{\prime}(t) = a_{21}y_{1}(t)+a_{22}y_{2}(t)+\cdots+a_{2n}y_{n}(t)+f_{2}(t)\\[0.7em]
\quad\vdots\\[0.7em]
y_{n}^{\prime}(t) = a_{n1}y_{1}(t)+a_{n2}y_{2}(t)+\cdots+a_{nn}y_{n}+f_{n}(t)
\end{cases}\label{非同次系}
\end{align}
まず前提として,線形微分方程式を瞬殺する必殺奥義で説明している通り,非同次系の微分方程式の解は同次系の一般解と非同次系の特殊解の和として求められます。同次系の一般解の求め方は上で解説しましたので,ここでは非同次系の特殊解の求め方を確認します。対称系非同次系連立微分方程式の特殊解を求める方法には係数変化法と微分演算子によるアプローチがあり,対称系の場合は例外として少し違ったアプローチをします。まずは対称系から確認します。
対称系
$n=2$において,次の形の連立微分方程式は「和と差」を考えることで解くことができます。
\begin{cases}
x^{\prime} = px+qy+f_{1}(t)\\[0.7em]
y^{\prime} = qx+py+f_{2}(t)
\end{cases}
\end{align}
具体的な対称系の連立微分方程式として,次を考えてみましょう。
\begin{cases}
x^{\prime} = 2x+y+e^{-t}\\[0.7em]
y^{\prime} = x+2y+e^{2t}
\end{cases}
\end{align}
和と差を考えることで,
\begin{cases}
x^{\prime}+y^{\prime} = 3(x+y)+e^{-t}+e^{2t}\\[0.7em]
x^{\prime}-y^{\prime} = (x-y)+e^{-t}-e^{2t}
\end{cases}\label{和と差}
\end{align}
が得られます。同次系の連立微分方程式
\begin{cases}
x^{\prime}+y^{\prime} = 3(x+y)\\[0.7em]
x^{\prime}-y^{\prime} = (x-y)
\end{cases}
\end{align}
を考えると,いずれも単純に解くことができて,
\begin{cases}
x+y = Ae^{3t}\\[0.7em]
x-y = Be^{t}\\[0.7em]
\end{cases}
\end{align}
となります。非同次系の和
x^{\prime}+y^{\prime} = 3(x+y)+e^{-t}+e^{2t}
\end{align}
について,$e^{-t}+e^{2t}$も含めて「同次系のように」扱うため,
(x+y+\alpha e^{-t}+\beta e^{2t})^{\prime}=3(x+y+\alpha e^{-t}+\beta e^{2t})\label{和_alpha_beta}
\end{align}
と変形します。この形は先ほど解いた同次系の解と一致しますので,$\alpha$と$\beta$は求められれば
x+y+\alpha e^{-t}+\beta e^{2t}
&= Ae^{3t}\label{alpha_beta_解の求め方}
\end{align}
が得られます。式($\ref{和_alpha_beta}$)を展開すると
x^{\prime}+y^{\prime}
&= 3(x+y)+4\alpha e^{-t}+\beta e^{2t}
\end{align}
となるため,式($\ref{和と差}$)と係数を比較することにより$(\alpha,\beta)=(1/4,1)$が得られます。これらを式($\ref{alpha_beta_解の求め方}$)に代入することにより,
x+y+\frac{1}{4} e^{-t}+e^{2t}
&= Ae^{3t}\label{和}
\end{align}
が得られます。差に関しても同様に計算することにより,
x-y+\frac{1}{2} e^{-t}+e^{2t}
&= Be^{t}\label{差}
\end{align}
が得られます。式($\ref{和}$)と式($\ref{差}$)の和と差を考えることにより,
\begin{cases}
\displaystyle
x = c_{1}e^{3t}+c_{2}e^{t}-\frac{3}{8}e^{-t}-e^{2t}\\[0.7em]
\displaystyle
y = c_{1}e^{3t}-c_{2}e^{t}+\frac{1}{8}e^{-t}
\end{cases}
\end{align}
が得られます。ただし,$(c_{1},c_{2})=(A/2,B/2)$と置きました。
係数変化法
\begin{cases}
x^{\prime} = 2x-y+e^{2t}\\[0.7em]
y^{\prime} = 5x-4y+e^{-t}
\end{cases}
\end{align}
同次系の連立微分方程式
\begin{cases}
x^{\prime} = 2x-y\\[0.7em]
y^{\prime} = 5x-4y
\end{cases}
\end{align}
の固有方程式は$\lambda=-3,1$の解を持ち,それぞれの固有ベクトルは
- $\lambda=-3$のとき:$(x,y)=(e^{-3t},5e^{-3t})$
- $\lambda=1$のとき:$(x,y)=(e^{t},e^{t})$
となりますので,同次系の一般解$(x_{c},y_{c})$は
\begin{cases}
x_{c}=c_{1}e^{t}+c_{2}e^{-3t}\\[0.7em]
y_{c}=c_{1}e^{t}+5c_{2}e^{-3t}
\end{cases}\label{同次系_一般解}
\end{align}
となります。定数変化法では,同次系の一般解の係数を$t$の関数として置き直したものを連立微分方程式の解とみなすのでした。
\begin{cases}
x=u_{1}(t)e^{t}+u_{2}(t)e^{-3t}\\[0.7em]
y=u_{1}(t)e^{t}+5u_{2}(t)e^{-3t}
\end{cases}\label{定数変化法}
\end{align}
与えられた連立微分方程式に代入して整理すると
\begin{cases}
\displaystyle
u_{1}^{\prime}(t)=\frac{1}{4}\left(5e^{t}-e^{-2t}\right)\\[0.7em]
\displaystyle
u_{2}^{\prime}(t)=\frac{1}{4}\left(e^{2t}-e^{5t}\right)
\end{cases}
\end{align}
となるため,両辺を$t$で積分することにより,
\begin{cases}
\displaystyle
u_{1}(t)=\frac{1}{4}\left(5e^{t}+\frac{1}{2}e^{-2t}\right)+c_{1}\\[0.7em]
\displaystyle
u_{2}(t)=\frac{1}{4}\left(\frac{1}{2}e^{2t}-\frac{1}{5}e^{5t}\right)+c_{2}
\end{cases}
\end{align}
が得られます。式($\ref{定数変化法}$)に代入すれば
\begin{cases}
\displaystyle
x = c_{1}e^{t}+c_{2}e^{-3t}+\frac{6}{5}e^{2t}+\frac{1}{4}e^{-t}\\[0.7em]
\displaystyle
y = c_{1}e^{t}+5c_{2}e^{-3t}+e^{2t}+\frac{3}{4}e^{-t}
\end{cases}
\end{align}
となります。
微分演算子
定数変化法を用いた解法は,計算がやや煩雑になりがちです。そこで,線形微分方程式を瞬殺する必殺奥義で徹底解説している微分演算子法を用いることを考えます。先ほどの問題を微分演算子を用いて表します。
\begin{cases}
(D-2)x+y = e^{2t}\\[0.7em]
-5x+(D+4)y = e^{-t}
\end{cases}\label{微分演算子}
\end{align}
上式に$(D+4)$を掛けて$y$を消去すると,
(D-2)(D+4)x+5x &= 6e^{2t}-e^{-t}D^2+2D+3
\end{align}
が得られます。これに微分演算子法の指数関数に対する解法を適用すれば,$x$の特殊解$X$は
X
&= \frac{6}{(D+3)(D-1)}[e^{2t}]-\frac{1}{(D+3)(D-1)}[e^{-t}]
= \frac{6}{5}e^{2t}+\frac{1}{4}e^{-t}
\end{align}
となります。これを式($\ref{微分演算子}$)の上式に代入すれば,
Y
&= e^{2t}-(D-2)x\\[0.7em]
&= e^{2t}-\left(\frac{12}{5}e^{2t}-\frac{1}{4}e^{-t}\right)+\left(\frac{12}{5}e^{2t}+\frac{1}{2}e^{-t}\right)
= \frac{3}{4}e^{-t}
\end{align}
が得られます。これらと同次系の一般解($\ref{同次系_一般解}$)より,求める答えは
\begin{cases}
\displaystyle
x = x_{c} + X = c_{1}e^{t}+c_{2}e^{-3t}+\frac{6}{5}e^{2t}+\frac{1}{4}e^{-t}\\[0.7em]
\displaystyle
y = y_{c} + Y = c_{1}e^{t}+5c_{2}e^{-3t}+e^{2t}+\frac{3}{4}e^{-t}
\end{cases}
\end{align}
となります。
補足
一般に,非同次系の微分方程式を
\begin{cases}
P_{11}(D)y_{1}+P_{12}(D)y_{2}+\cdots+P_{1n}(D)y_{n}=f_{1}(t)\\[0.7em]
P_{21}(D)y_{1}+P_{22}(D)y_{2}+\cdots+P_{2n}(D)y_{n}=f_{2}(t)\\[0.7em]
\quad\vdots\\[0.7em]
P_{n1}(D)y_{1}+P_{n2}(D)y_{2}+\cdots+P_{nn}(D)y_{n}=f_{n}(t)
\end{cases}\label{非同次系_一般}
\end{align}
と書き,$(i,j)$成分を$P(ij)(D)$とする係数行列の行列式を$\Delta(D)$と置くと,
\Delta(D)=
\begin{vmatrix}
P_{11}(D)&\cdots&P_{1n}(D)\\
\vdots&\ddots&\vdots\\
P_{n1}(D)&\cdots&P_{nn}(D)
\end{vmatrix}
\end{align}
と表されます。$P_{ij}(D)$の余因子を$\Delta_{ij}(D)$と表すと,第一列の余因子展開より
\Delta(D)=\Delta_{11}(D)P_{11}(D)+\cdots+\Delta_{n1}(D)P_{n1}(D)
\end{align}
が得られます。ここで,行列式に同一の列が存在する場合行列式は$0$となるため,第二列を第一列にコピーした上で第一列の余因子展開を行うことにより,
0=\Delta_{11}(D)P_{12}(D)+\cdots+\Delta_{n1}(D)P_{n2}(D)
\end{align}
が得られます。同様に第$i$列を第一列にコピーして余因子展開を行うことにより,
\begin{cases}
\Delta_{11}(D)P_{11}(D)+\cdots+\Delta_{n1}(D)P_{n1}(D)=\Delta(D)\\[0.7em]
\Delta_{11}(D)P_{12}(D)+\cdots+\Delta_{n1}(D)P_{n2}(D)=0\\[0.7em]
\quad\vdots\\[0.7em]
\Delta_{11}(D)P_{1n}(D)+\cdots+\Delta_{nn}(D)P_{nn}(D)=0
\end{cases}
\end{align}
が得られます。式($\ref{非同次系_一般}$)において,第$i$式$\times\Delta_{1i}(D)$を考えることで,
\begin{cases}
\Delta(D)y_{1}=\Delta_{11}(D)f_{1}(t)+\cdots+\Delta_{n1}(D)f_{n}(t)\\[0.7em]
\Delta(D)y_{2}=\Delta_{12}(D)f_{1}(t)+\cdots+\Delta_{n2}(D)f_{n}(t)\\[0.7em]
\quad\vdots\\[0.7em]
\Delta(D)y_{n}=\Delta_{1n}(D)f_{1}(t)+\cdots+\Delta_{nn}(D)f_{n}(t)
\end{cases}\label{微分演算子_公式}
\end{align}
が得られます。これは「$y$は$f$に$D$の逆演算子を適用すれば求められる」ことを意味しています。すなわち,$y$は$\Delta(D)$の次数分だけ積分操作をすることにより得られるため,$y$の任意定数の個数は$\Delta(D)$の次数と等しくなります。例えば,$3$次行列において$\Delta(D)$の次数が$2$である場合,任意定数は$2$つとなりますので,任意定数を$c_{1},c_{2},c_{3}$と置いた場合には任意定数同士に関する条件が$1$つ得られるため,いずれかの任意定数を$1$つ削除する必要がある点に注意してください。次の具体例を通じて理解を促進しましょう。
\begin{cases}
Dx+(D+1)y=1\\[0.7em]
(D+2)x-(D-1)z=1\\[0.7em]
(D+1)y+(D+2)z=0
\end{cases}
\end{align}
まず$\Delta(D)$を計算すると,
\Delta(D)=
\begin{vmatrix}
D&D+1&0\\
D+2&0&-D+1\\
0&D+1&D+2
\end{vmatrix}
= -5D^{2}-9D-4
\end{align}
となるため,任意定数の個数は$2$つとなります。一方,式($\ref{微分演算子_公式}$)より
\begin{cases}
\Delta(D)[x]=(D-1)(D+1)[1]-(D+1)(D+2)[1]\\[0.7em]
\Delta(D)[y]=-(D+2)^{2}[1]+D(D+2)[1]\\[0.7em]
\Delta(D)[z]=(D+2)(D+1)[1]-D(D+1)[1]
\end{cases}
\end{align}
となるため,微分演算子法の指数関数に対する解法を適用すれば,
\begin{cases}
\displaystyle
x
=-\frac{D-1}{(5D+4)}[e^{0}]+\frac{D+2}{(5D+4)}[e^{0}]
=c_{1}e^{-(4/5)t}+\frac{3}{4}\\[0.7em]
\displaystyle
y=\frac{(D+2)^{2}}{(D+1)(5D+4)}[e^{0}]-\frac{D(D+2)}{(D+1)(5D+4)}[e^{0}]
=c_{2}e^{-t}+c_{3}e^{-(4/5)t}+1\\[0.7em]
\displaystyle
z
=-\frac{D+2}{5D+4}[e^{0}]+\frac{D}{5D+4}[e^{0}]
=c_{4}e^{-(4/5)t}-\frac{1}{2}
\end{cases}
\end{align}
が得られます。任意定数は$2$個で表されるため,$c_{1},c_{2},c_{3},c_{4}$のうち$2$つを削除しなくてはなりません。与えられた式の第一式に$x,y$を代入することにより,
\frac{1}{5}(c_{3}-4c_{1})e^{-(4/5)t}=0
\end{align}
が得られるため$c_{3}=4c_{1}$となります。同様に,与えられた式の第二式に$x,z$を代入することにより,
\frac{3}{5}(2c_{1}+3c_{4})e^{-(4/5)t}=0
\end{align}
が得られるため$\displaystyle c_{4}=-\frac{2}{3}c_{1}$となります。以上より,
\begin{cases}
\displaystyle
x
=c_{1}e^{-(4/5)t}+\frac{3}{4}\\[0.7em]
\displaystyle
y
=c_{2}e^{-t}+4c_{1}e^{-(4/5)t}+1\\[0.7em]
\displaystyle
z
=-\frac{2}{3}c_{1}e^{-(4/5)t}-\frac{1}{2}
\end{cases}
\end{align}
が得られます。
一般系
次の形の連立微分方程式を一般系と呼ぶことにします。
\frac{dx}{P(x,y,z)} = \frac{dy}{Q(x,y,z)} = \frac{dz}{P(x,y,z)}
\end{align}
一般系の連立微分方程式は解くことが難しいケースが多いですが,
\frac{dy}{dx} = \frac{Q(x,y,z)}{P(x,y,z)},\quad
\frac{dz}{dx} = \frac{R(x,y,z)}{P(x,y,z)},\quad
\frac{dz}{dy} = \frac{R(x,y,z)}{Q(x,y,z)}
\end{align}
がシンプルな形になる場合は,任意定数を$2$つ用いて解を求めることができます。
\frac{dx}{xy} = \frac{dy}{y} = \frac{dz}{z}
\end{align}
第一式と第二式より,
\frac{dx}{x} = dy
\end{align}
を得るため,両辺を積分して
\log|x| = y + c_{1}
\end{align}
となります。$\pm e^{c_{1}}$を改めて$c_{1}$とおくと,$x=c_{1}e^{y}$が得られます。同様に,第二式と第三式より$y=c_{2}z$となります。以上より,求める答えは
x=c_{1}e^{y},\quad y=c_{2}z
\end{align}
となります。一般系の連立微分方程式を解くことができるケースとして,本稿では比例式を用いる方法と加比の理を用いる方法の2つを紹介します。
比例式
比例式の考えを用いた一般系の連立微分方程式の解法では,
\frac{dx}{P(x,y,z)} = \frac{dy}{Q(x,y,z)} = \frac{dz}{P(x,y,z)} = dt
\end{align}
とおくことで,同次系の連立微分方程式に帰着させることができます。次の問題を考えます。
\frac{dx}{x+y-z} = \frac{dy}{z} = \frac{dz}{2y+z}
\end{align}
与式を$dt$とおくと,
\begin{cases}
x^{\prime} = x+y-z\\[0.7em]
y^{\prime} = z\\[0.7em]
z^{\prime} = dy+z
\end{cases}
\end{align}
という同次系の連立微分方程式が得られます。固有方程式は$\lambda=-1,1,2$の解を持ち,それぞれの固有ベクトルは
- $\lambda=-1$のとき:$(x,y,z)=(e^{-t},-e^{t},e^{-t})$
- $\lambda=1$のとき:$(x,y,z)=(e^{t},0,0)$
- $\lambda=2$のとき:$(x,y,z)=(e^{2t},-e^{2t},-2e^{2t})$
となりますので,
\begin{cases}
x = c_{1}e^{-t}+c_{2}e^{t}+c_{3}e^{2t}\\[0.7em]
y = -c_{1}e^{-t}-c_{3}e^{2t}\\[0.7em]
z = c_{1}e^{-t}-2c_{3}e^{2t}
\end{cases}
\end{align}
が得られます。$t$を削除するため
\begin{cases}
-3c_{1}e^{-t} = 2y-z\\[0.7em]
c_{2}e^{t} = x+y\\[0.7em]
-3c_{3}e^{2t} = y+z
\end{cases}
\end{align}
と変形すると,求める答えは
\begin{cases}
(2y-z)(x+y) = -3c_{1}c_{2} = c_{1}^{\prime}\\[0.7em]
(2y-z)^{2}(y+z)=-27c_{1}^{2}c_{3} = c_{2}^{\prime}
\end{cases}
\end{align}
となります。
加比の理
次の形をした微分方程式
\frac{df(d,y,z)}{f(x,y,z)}\label{加比の理_目標}
\end{align}
は,$\log$の微分より$\log|f(x,y,z)|$と簡単に解くことができます。連立微分方程式から式($\ref{加比の理_目標}$)の形を抽出する際に活躍するのが以下の加比の理と呼ばれる性質です。
一般に,式$a_{i},p_{i}(i=1,2,3)$に対して
\frac{a_{1}}{p_{1}}
= \frac{a_{2}}{p_{2}}
= \frac{a_{3}}{p_{3}}
= k
\end{align}
のとき,
\frac{la_{1}+ma_{2}+na_{3}}{lp_{1}+mp_{2}+np_{3}} = k
\end{align}
が成り立つ。
次の問題を通して具体的にみていきましょう。
\frac{dx}{2x-2y+2z} = \frac{dy}{x+y} = \frac{dz}{x+3y-2z}
\end{align}
式($\ref{加比の理_目標}$)と同じ形の
\frac{ldx+mdy+ndz}{\lambda(lx+my+nz)}
= \frac{d(lm+my+nz)}{\lambda(lx+my+nz)}\label{問題_目標}
\end{align}
を作ることができれば都合が良いのでした。与式を$k$とおくと,加比の理より
k
&= \frac{ldx}{l(2x-2y+2z)}
= \frac{mdy}{m(x+y)}
= \frac{ndz}{n(x+3y-2z)}\\[0.7em]
&= \frac{ldx+mdy+ndz}{l(2x-2y+2z)+m(x+y)+n(x+3y-2z)}\\[0.7em]
&= \frac{d(lx+my+nz)}{(2l+m+n)x+(-2l+m+2n)y+(2l-2n)z}
\end{align}
が成り立つため,これが式($\ref{問題_目標}$)の形となるような$l,m,n,\lambda$を求めることを考えます。式($\ref{問題_目標}$)との恒等式を立てれば$x,y,z$の係数比較により$3$つの条件が得られるため,$3$つの解が得られることを期待します。実際,
\frac{d(lx+my+nz)}{(2l+m+n)x+(-2l+m+2n)y+(2l-2n)z}
= \frac{d(lm+my+nz)}{\lambda(lx+my+nz)}
\end{align}
の係数比較により得られる
\begin{cases}
2l+m+n = \lambda l\\[0.7em]
-2l+m+3n = \lambda m\\[0.7em]
2l-2n = \lambda n
\end{cases}
\end{align}
を変形すると
\begin{pmatrix}
2&1&1\\
-2&1&3\\
2&0&-2
\end{pmatrix}
\begin{pmatrix}
l\\
m\\
n
\end{pmatrix}
\equiv Ax
= \lambda
\begin{pmatrix}
l\\
m\\
n
\end{pmatrix}
\end{align}
となるため,$A$の固有値問題に帰着します。実際に固有値と固有ベクトルを求めると
- $\lambda=-2$のとき:$(l,m,n)=(0,1,-1)t$
- $\lambda=1$のとき:$(l,m,n)=(3,-5,2)t$
- $\lambda=2$のとき:$(l,m,n)=(2,-1,1)t$
となるため,
k
= \frac{d(y-z)}{-2(y-z)}
= \frac{d(3x-5y+2z)}{3x-5y+2z}
= \frac{d(2x-y+z)}{2(2x-y+z)}
\end{align}
と表すことができました。第一式と第二式の両辺を積分すると
\log|y-z|+2\log|3x-5y+2z| = c_{1}^{\prime}
\end{align}
となるため,$c_{1}=\pm e^{c_{1}^{\prime}}$とおけば
(y-z)(3x-5y+2z)^{2} = c_{1}
\end{align}
が得られます。同様に,第一式と第三式の両辺を積分すると
\log|y-z|+\log|2x-y+z| = c_{2}^{\prime}
\end{align}
となるため,$c_{2}=\pm e^{c_{2}^{\prime}}$とおけば
(y-z)(2x-y+z) = c_{2}
\end{align}
が得られます。以上より,求める答えは
\begin{cases}
(y-z)(3x-5y+2z)^{2} = c_{1}\\[0.7em]
(y-z)(2x-y+z) = c_{2}
\end{cases}
\end{align}
となります。
行列への拡張
$n$次元正方行列$A$に対し,
e^{A}
&= E+\frac{1}{1!}A+\frac{1}{2!}A^{2}+\cdots+\frac{1}{k!}A^{k}+\cdots
\end{align}
で定義される行列を$A$の指数行列という。特に,$A=PBP^{-1}$のとき,
e^{PBP^{-1}}
&= E+\frac{1}{1!}PBP^{-1}+\frac{1}{2!}PB^{2}P^{-1}+\cdots+\frac{1}{k!}PB^{k}P^{-1}+\cdots\\[0.7em]
&= P(E+\frac{1}{1!}B+\frac{1}{2!}B^{2}+\cdots+\frac{1}{k!}B^{k}+\cdots)P^{-1}\\[0.7em]
&= Pe^{B}P^{-1}\label{指数行列_性質}
\end{align}
となる。
$A=PBP^{-1}$は$A$を$B$に対角化する操作,もしくはジョルダン標準形に変換する操作のことを指しています。
指数行列とその性質を利用して連立微分方程式を解くことができます。本稿では対角化可能な場合を扱いますが,対角化不能な場合の扱いは本稿最下部の参考書籍をご参照ください。
\begin{cases}
x^{\prime} = x-z\\[0.7em]
y^{\prime} = x+2y+z\\[0.7em]
z^{\prime} = 2x+2y+3z
\end{cases}
\end{align}
まず,
\vx =
\begin{pmatrix}
x(t)\\
y(t)\\
z(t)
\end{pmatrix},\quad
A =
\begin{pmatrix}
1 & 0 & -1\\
1 & 2 & 1\\
2 & 2 & 3
\end{pmatrix}
\end{align}
とおくと与式は$\vx^{\prime}=A\vx$と表され,この微分方程式の一般解は$\vc=(c_{1},c_{2},c_{3})^{T}$を用いて
\vx = e^{tA}\vc\label{指数行列_一般解}
\end{align}
と表されます。$A$の固有方程式を解いて対角化すると,
P=
\begin{pmatrix}
1 & -2 & 1\\
-1 & 1 & -1\\
0 & 2 & -2
\end{pmatrix},\quad
B=
\begin{pmatrix}
1 & 0 & 0\\
0 & 2 & 0\\
0 & 0 & 3
\end{pmatrix}
\end{align}
とおいて$A=PBP^{-1}$と表されるため,式($\ref{指数行列_性質}$)を用いて$P^{-1}\vc$を$\vc$と置き直すと式($\ref{指数行列_一般解}$)は
\vx
= e^{t(PBP^{-1})}\vc
= e^{P(tB)P^{-1}}\vc
= Pe^{tB}P^{-1}\vc
= Pe^{tB}\vc
\end{align}
となります。ここで,
e^{tB}
&= E+\frac{1}{1!}
\begin{pmatrix}
t & 0 & 0\\
0 & 2t & 0\\
0 & 0 & 3t
\end{pmatrix}
+\cdots+
\frac{1}{k!}
\begin{pmatrix}
t^{k} & 0 & 0\\
0 & (2t)^{k} & 0\\
0 & 0 & (3t)^{k}
\end{pmatrix}
+\cdots\\[0.7em]
&=
\begin{pmatrix}
\displaystyle\sum_{k=1}^{\infty}\frac{t^{k}}{k!} & 0 & 0\\
0 & \displaystyle\sum_{k=1}^{\infty}\frac{(2t)^{k}}{k!} & 0\\
\displaystyle
0 & 0 & \displaystyle\sum_{k=1}^{\infty}\frac{(3t)^{k}}{k!}
\end{pmatrix}
=
\begin{pmatrix}
e^{t} & 0 & 0\\
0 & e^{2t} & 0\\
0 & 0 & e^{3t}
\end{pmatrix}
\end{align}
に注意すると,
\vx
&=
\begin{pmatrix}
1 & -2 & 1\\
-1 & 1 & -1\\
0 & 2 & -2
\end{pmatrix}
\begin{pmatrix}
e^{t} & 0 & 0\\
0 & e^{2t} & 0\\
0 & 0 & e^{3t}
\end{pmatrix}
\begin{pmatrix}
c_{1}\\
c_{2}\\
c_{3}
\end{pmatrix}\\[0.7em]
&=
\begin{pmatrix}
c_{1}e^{t}-2c_{2}e^{2t}+c_{3}e^{3t}\\
-c_{1}e^{t}+c_{2}e^{2t}-c_{3}e^{3t}\\
2c_{2}e^{2t}-2c_{3}e^{3t}
\end{pmatrix}
\end{align}
が得られるため,求める答えは
\begin{cases}
x=c_{1}e^{t}-2c_{2}e^{2t}+c_{3}e^{3t}\\[0.7em]
y=-c_{1}e^{t}+c_{2}e^{2t}-c_{3}e^{3t}\\[0.7em]
z=2c_{2}e^{2t}-2c_{3}e^{3t}
\end{cases}
\end{align}
となります。
非同次系の連立微分方程式に対しても,指数行列による解法を利用することができます。
\begin{cases}
x^{\prime} = -y+t\\[0.7em]
y^{\prime} = -x+2
\end{cases}\quad
x(0)=0
y(0)=1
\end{align}
まず,
\vx =
\begin{pmatrix}
x(t)\\
y(t)
\end{pmatrix},\quad
A =
\begin{pmatrix}
0 & -1\\
-1 & 0
\end{pmatrix},\quad
\vb =
\begin{pmatrix}
t\\
2
\end{pmatrix}
\end{align}
とおくと与式は$\vx^{\prime}=A\vx+\vb$と表され,この微分方程式の一般解は$\vc=(c_{1},c_{2},c_{3})^{T}$を用いて
\vx = e^{tA}\left(\int e^{-tA}\vb~dt+\vc\right)
\label{指数行列_一般解_非同次}
\end{align}
と表されます。$A$の固有方程式を解いて対角化すると,
P=
\begin{pmatrix}
1 & 1\\
-1 & 1
\end{pmatrix},\quad
B=
\begin{pmatrix}
1 & 0\\
0 & -1
\end{pmatrix}
\end{align}
とおいて$A=PBP^{-1}$と表されるため,同次系のときと同様に
e^{tA}
&= Pe^{tB}P^{-1}
=
\begin{pmatrix}
1 & 1\\
-1 & 1
\end{pmatrix}
\begin{pmatrix}
e^{t} & 0\\
0 & e^{-t}
\end{pmatrix}
\frac{1}{2}
\begin{pmatrix}
1 & -1\\
1 & 1
\end{pmatrix}\\[0.7em]
&= \frac{1}{2}
\begin{pmatrix}
e^{t}+e^{-t} & -e^{t}+e^{-t}\\
-e^{t}+e^{-t} & e^{t}+e^{-t}
\end{pmatrix}
\end{align}
となります。いま,積分定数を省略すると
\int te^{t}dt = (t-1)e^{t},\quad
\int te^{-t}dt = (-t+1)e^{-t},\quad
\int -te^{-t}dt = (t+1)e^{-t}
\end{align}
となることに注意して式($\ref{指数行列_一般解_非同次}$)の積分を要素ごとに計算すると,
\int e^{-tA}\vb~dt
&= \frac{1}{2}\int
\begin{pmatrix}
e^{t}+e^{-t} & e^{t}-e^{-t}\\
e^{t}-e^{-t} & e^{t}+e^{-t}
\end{pmatrix}
\begin{pmatrix}
t\\
2
\end{pmatrix}
dt \\[0.7em]
&=
\frac{1}{2}\int
\begin{pmatrix}
(t+2)e^{t} + (t-2)e^{-t}\\
(t+2)e^{t} - (t-2)e^{-t}
\end{pmatrix}
dt\\[0.7em]
&=
\frac{1}{2}
\begin{pmatrix}
(t+1)e^{t} - (t-1)e^{-t}\\
(t+1)e^{t} + (t-1)e^{-t}
\end{pmatrix}
\end{align}
となるため,式($\ref{指数行列_一般解_非同次}$)は
\vx =
\frac{1}{2}
\begin{bmatrix}
e^{t}+e^{-t} & -e^{t}+e^{-t}\\
-e^{t}+e^{-t} & e^{t}+e^{-t}
\end{bmatrix}
\left(
\frac{1}{2}
\begin{bmatrix}
(t+1)e^{t} - (t-1)e^{-t}\\
(t+1)e^{t} + (t-1)e^{-t}
\end{bmatrix}
+
\begin{bmatrix}
c_{1}\\
c_{2}
\end{bmatrix}
\right)
\end{align}
となります。これに初期条件を代入すれば$(c_{1},c_{2})=(-1,1)$が得られるため,行列積を計算することにより
\begin{bmatrix}
x(t)\\
y(t)
\end{bmatrix}
&=
\frac{1}{4}
\begin{bmatrix}
e^{t}+e^{-t} & -e^{t}+e^{-t}\\
-e^{t}+e^{-t} & e^{t}+e^{-t}
\end{bmatrix}
\begin{bmatrix}
(t+1)e^{t} - (t-1)e^{-t}-2\\
(t+1)e^{t} + (t-1)e^{-t}+2
\end{bmatrix}\\[0.7em]
&=
\frac{1}{4}
\begin{bmatrix}
-2(t-1)-4e^{t}+2(t+1)\\
2(t-1)+4e^{t}+2(t+1)
\end{bmatrix}
=
\begin{bmatrix}
1-e^{t}\\
t+e^{t}
\end{bmatrix}
\end{align}
が得られます。
最後の行列積は煩雑な計算と思いきや,対称性があるため多くの項が相殺されます。




コメント