本稿では，代表的な微分方程式の解法をお伝えします。
初学者の分かりやすさを優先するため，多少正確でない表現が混在することがあります。もし致命的な間違いがあればご指摘いただけると助かります。
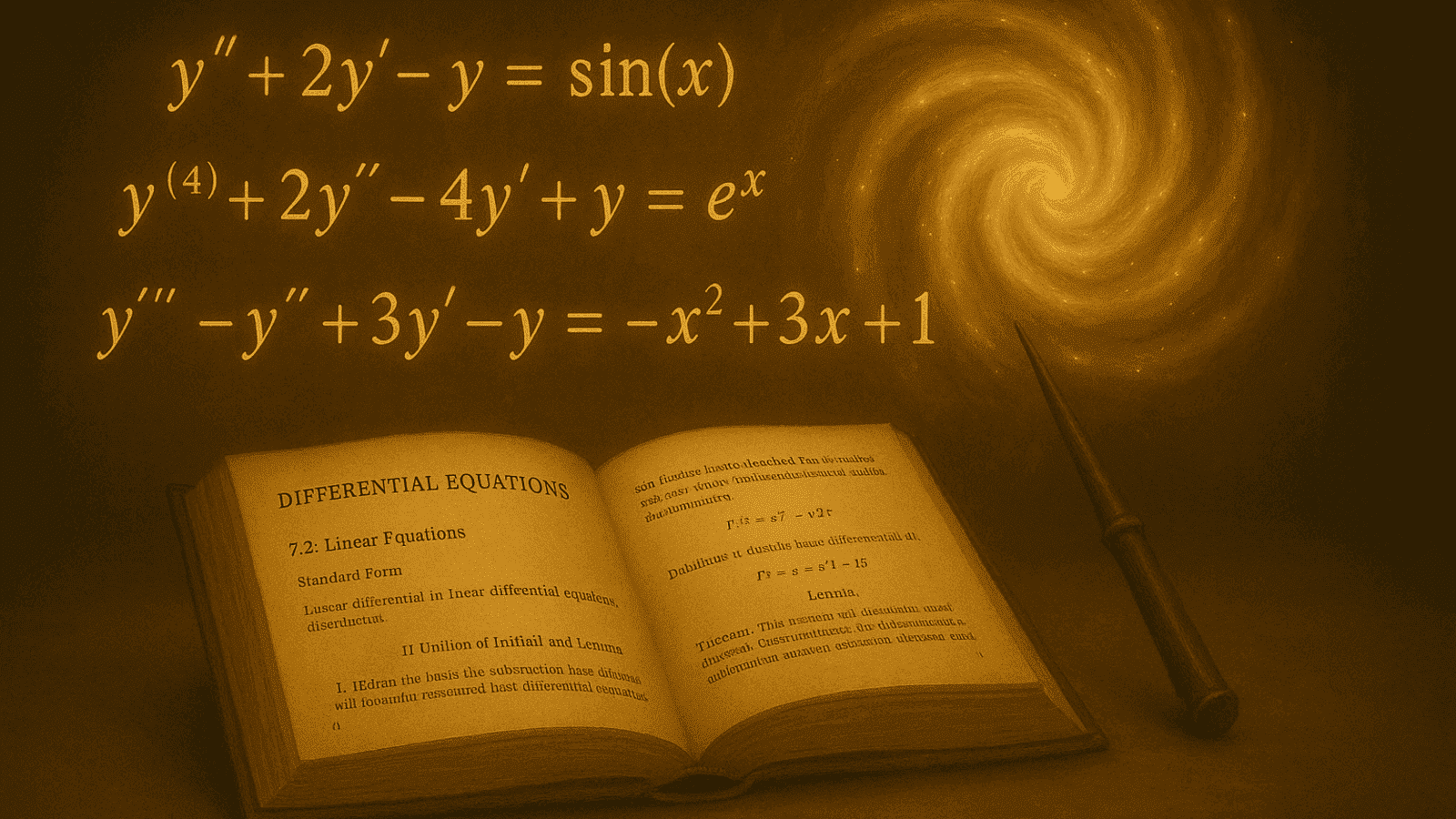
一階線形微分方程式
次の形をした微分方程式を，一階線形微分方程式と呼びます。
\frac{dy}{dx} + P(x)y &= Q(x) \label{主題}
\end{align}
一階線形微分方程式は一階非同次形微分方程式とも呼ばれます。この場合の「同次」は同次系の微分方程式とは異なる意味で同次という用語を用いているため注意が必要です。
解法
一階線形微分方程式は，二階線形微分方程式と同様に定数変化法でアプローチすることが可能です。しかし，多くの参考書では異なるアプローチをとり，本記事でもそれに従います。数検1級の範囲では「定数係数」の二階線形微分方程式が出題されることがほとんどだからです。仮に「変数係数」が出題されたとしてもオイラーの微分方程式の形をしていることがほとんどですので，定数変化法を用いてロンスキー行列を持ち出す必要はありません。
一方で，一階線形微分方程式では定数係数のケースはもちろん，変数係数のケースも出題されます。二階線形微分方程式の右辺は「多項式」「指数関数」「三角関数」の組み合わせで構成されることがほとんどですが，一階線形微分方程式の右辺はそれ以外の関数も出てきます。
このような一階線形微分方程式の解法として，素朴に考えると定数変化法を持ち出す必要がありますが，定数変化法を用いた一階線形微分方程式の対策は数検1級の文脈においてはオーバーキルです。二階微分方程式の一般的な解法である定数変化法を一階微分方程式に当てはめるという対策は，数検1級においては推奨されないと考えています。
ロンスキー行列を持ち出さずに，単に$C$を$C(x)$とみなす解法はおさえておいてもよいでしょう。
そこで，一階線形微分方程式特有の解法を身につけましょう。無理矢理「積の微分」の形を作ってあげるのです。具体的にみていきましょう。一階線形微分方程式は以下のような形をしていました。
\frac{dy}{dx} + P(x)y &= Q(x)
\end{align}
左辺を積の微分の形に近づけることが目標です。まず，左辺にある2つの項の両方に$y$が出現していることに注目します。第一項目は$y$を微分していて，第二項目は$y$がそのまま出現しています。これは，以下の積の微分
(yx)^{\prime} &= y^{\prime}x + x^{\prime}y
\end{align}
の形に似ていることに着目します。微分して$P(x)$が出てくるような関数を$x$として利用すればよさそうです。微分して$P(x)$が出てくるような関数には何があるでしょうか。ここでは，微分方程式で大活躍する指数関数$e^{x}$を利用します。天下り的ですが，$\exp{\int P(x) dx}$を考えると$x$で微分したときに肩の$P(x)$が前に出てきてくれます。$\exp{\int P(x) dx}$を両辺に掛けると，
\frac{dy}{dx}\cdot e^{\int P(x) dx} + P(x)\cdot ye^{\int P(x) dx} &= Q(x)e^{\int P(x) dx}
\end{align}
となり，左辺は
\left( ye^{\int P(x) dx} \right)^{\prime} &= Q(x) e^{\int P(x) dx}
\end{align}
のように積の微分の形に帰着します。
$\exp{\int P(x) dx}$は積分因子とも呼ばれます。
両辺を$x$で積分します。
\int \left( ye^{\int P(x) dx} \right)^{\prime} dx &= \int Q(x) e^{\int P(x) dx} dx \\[0.7em]
ye^{\int P(x) dx} &= \int Q(x) e^{\int P(x) dx} dx + C
\end{align}
したがって，一階線形微分方程式は
y &= e^{-\int P(x) dx} \left( \int Q(x) e^{\int P(x) dx} dx + C \right)
\end{align}
のように一般解を求めることができます。
この式を覚える必要はありません。一階線形微分方程式では，左辺を積の形に持っていくために指数関数を利用するということを理解してください。
例題
次の例題を解きましょう。ただし$a > 0$とし，初期条件は与えないため定数項はそのまま残してよいです。
(x^2 + a^2)y^{\prime} + xy &= 1
\end{align}
両辺を$x^{2}+a^{2}\neq 0$で割ると，
y^{\prime} + \frac{x}{x^2 + a^2}y &= \frac{1}{x^2 + a^2}
\end{align}
となります。左辺を積の微分の形に近づけるため，指数関数を利用します。
y^{\prime}\cdot e^{\int x/(x^2 + a^2) dx} + \frac{x}{x^2 + a^2}\cdot ye^{\int x/(x^2 + a^2) dx}
&= \frac{1}{x^2 + a^2}e^{\int x/(x^2 + a^2) dx} \\[0.7em]
\left(e^{\int x/(x^2 + a^2) dx}y \right)^{\prime} &= e^{\int x/(x^2 + a^2) dx} \frac{1}{x^2 + a^2} \\[0.7em]
e^{\int x/(x^2 + a^2) dx}y &= \int e^{\int x/(x^2 + a^2) dx} \frac{1}{x^2 + a^2} dx \label{積の微分後}\\[0.7em]
\end{align}
ここで，
e^{\int x/(x^2 + a^2) dx}
&= e^{\log (x^2 + a^2)/2}
= \sqrt{x^2 + a^2}
\end{align}
となるため，これを式($\ref{積の微分後}$)に代入すると，
\sqrt{x^2 + a^2}y &= \int \frac{1}{\sqrt{x^2 + a^2}} dx
\end{align}
が得られます。$x + \sqrt{x^2 + a^2} > 0$に注意して次の積分公式
\int \frac{1}{\sqrt{x^2 + a}} dx &= \log \left|x + \sqrt{x^2 + a}\right| + C \\[0.7em]
\end{align}
を用いると，
\sqrt{x^2 + a^2}y
&= \log |x + \sqrt{x^2 + a^2}| + C
= \log \left(x + \sqrt{x^2 + a^2}\right) + C
\end{align}
が得られます。したがって，求める答えは
y &= \frac{1}{\sqrt{x^2 + a^2}}\left\{ \log (x + \sqrt{x^2 + a^2}) + C \right\}
\end{align}
となります。
コメント