本記事は数学の徹底解説シリーズに含まれます。
初学者の分かりやすさを優先するため,多少正確でない表現が混在することがあります。もし致命的な間違いがあればご指摘いただけると助かります。
次元定理(階数・退化次数の定理)
次元定理は階数・退化次数の定理ともよばれます。
証明
次元定理の証明のキモは,上図における「平行マーク」と「長さが等しいマーク」です。すなわち,$V$の次元$n$から核の次元$s$を除いた$V$の次元$n-s$が線型変換$F$によって「保持」されることで$W^{\prime}$の次元も$n-s$になるという部分が最大のポイントです。
それでは,証明を始めます。はじめに,例外的なケースを除外しましょう。$F$が零写像,すなわち全ての像が$0$となるとき,$W^{\prime}=\{0\}$となり,核の定義より$V^{\prime}=V$となります。このとき,式($\ref{主題}$)は成り立ちます。したがって,以下では$F$が零写像以外のケースを考えます。
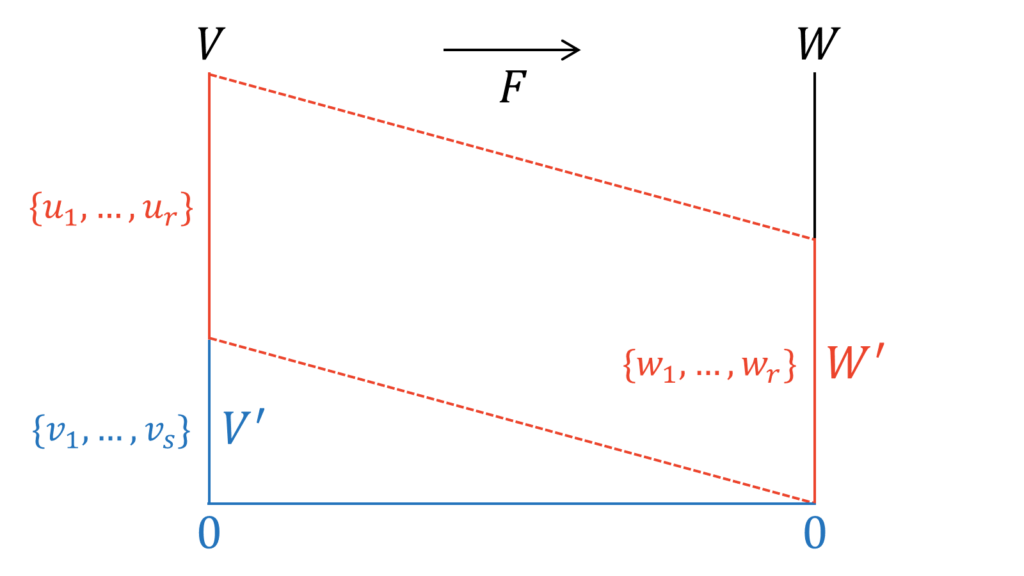
上図のように,$V^{\prime}$の一つの基底を$\vv=\{v_{1},\ldots,v_{s}\}$とします。すると,一次独立な元の集合と基底より,$V^{\prime}$の基底に$V$の元を加えることで$V$の残りの基底を作ることができるため,それらを$\vu=\{u_{1},\ldots,u_{r}\}$とおきます。ただし,$r=n-s$となります。さらに,$\vu$の$F$による像$F(\vu)$を$\vw=\{w_{1},\ldots,w_{r}\}$とおきます。いま,我々が示したいのは,$\vu$の次元と$\vw$の次元が等しくなることです。なぜなら,これらが等しくなること,すなわち$\dim W^{\prime}=r$となることで,
\dim W^{\prime} + \dim V^{\prime} &= r + s \\[0.7em]
&= (n-s) + s \\[0.7em]
&= n \\[0.7em]
&= \dim V
\end{align}
となり,式($\ref{主題}$)を示すことができるからです。したがって,以下では$\vu$の次元と$\vw$の次元が等しくなることを示します。基底の定義より,$\vu$の次元は$r$です。一方,現時点では$\vw$は$W^{\prime}$の基底となるとは限らないため,$\vw$の次元は$r$以下の値となります。逆に言えば,$\vw$が$W^{\prime}$の基底であることを示すことができれば,$\vw$の次元は$r$となり,式($\ref{主題}$)を示すことができます。したがって,以下では$\vw$が$W^{\prime}$の基底であることを示します。改めて基底の定義を再掲すると,$\vw$が以下を満たすことを示せばよいことになります。
- $W^{\prime}$の任意の元は$\vw$の一次結合で表される
- $\vw$は一次独立である
まずは,$W^{\prime}$の任意の元が$\vw$の一次結合で表されることを示します。先ほど,$\vv$を拡張して$V$の基底$\vu$を作ったことに注意すると,任意の実数$a_{1},\ldots,a_{s}$と$b_{1},\ldots,b_{r}$に対し,$V$の任意の元$v$は$\vv$と$\vu$の一次結合で表されます。
v &= a_{1}v_{1}+\cdots+a_{s}v_{s}+b_{1}u_{1}+\cdots+b_{r}u_{r}
\end{align}
このとき,$v$の$F$による像を考えます。$F$の線型性より,
F(v) &= F(a_{1}v_{1}+\cdots+a_{s}v_{s}+b_{1}u_{1}+\cdots+b_{r}u_{r}) \\[0.7em]
&= a_{1}F(v_{1})+\cdots+a_{s}F(v_{s})+b_{1}F(u_{1})+\cdots+b_{r}F(u_{r}) \\[0.7em]
&= b_{1}w_{1}+\cdots+b_{r}w_{r}
\end{align}
となります。したがって,$W^{\prime}$の任意の元$F(v)$は$\vw$の一次結合で表されることを示せました。次に,$\vw$が一次独立であることを示します。いま,実数$c_{1},\ldots,c_{r}$に対し
c_{1}w_{1}+\cdots+c_{r}w_{r} &= 0 \label{一次独立}
\end{align}
を考えます。このとき,$\vc$が全て$0$となることを示すことが目標です。$F$の線形性より,式($\ref{一次独立}$)の左辺は
c_{1}F(u_{1})+\cdots+c_{r}F(u_{r}) &= F(c_{1}u_{1}+\cdots+c_{r}u_{r})
\end{align}
となりますので,式($\ref{一次独立}$)は
F(c_{1}u_{1}+\cdots+c_{r}u_{r}) &= 0
\end{align}
と書き換えられます。すなわち,$c_{1}u_{1}+\cdots+c_{r}u_{r}$は$V$の核$V^{\prime}$に属しますので,実数$d_{1},\ldots,d_{s}$に対し,$\vv$の一次結合で表すことができます。
c_{1}u_{1}+\cdots+c_{r}u_{r} &= d_{1}v_{1}+\cdots+d_{s}v_{s}
\end{align}
両辺を整理すると,
(-d_{1})v_{1}+\cdots+(-d_{s})v_{s}+c_{1}u_{1}+\cdots+c_{r}u_{r} &= 0
\end{align}
となります。$\vv$と$\vu$はすべて一次独立ですので,$d_{1},\ldots,d_{s}$と$c_{1},\ldots,c_{r}$はすべて$0$でなければなりません。したがって,$\vw$は一次独立になります。以上で,$\vw$が$W^{\prime}$の基底であることを示せました。


コメント