【徹底解説】次元定理とは

本記事は数学の徹底解説シリーズに含まれます。

初学者の分かりやすさを優先するため，多少正確でない表現が混在することがあります。もし致命的な間違いがあればご指摘いただけると助かります。

次元定理（階数・退化次数の定理）

$V,W$をベクトル空間とし，$V$は有限次元であるとする。このとき，線型写像$F:~V\rightarrow W$の像を$W^{\prime}$，核を$V^{\prime}$とすれば，

\begin{align}
\dim W^{\prime} + \dim V^{\prime} &= \dim V \label{主題}
\end{align}

が成り立つ。すなわち，$F$の階数と$F$の退化次数の和は$V$の次元と等しくなる。

次元定理は階数・退化次数の定理ともよばれます。

証明

次元定理の証明のキモは，上図における「平行マーク」と「長さが等しいマーク」です。すなわち，$V$の次元$n$から核の次元$s$を除いた$V$の次元$n-s$が線型変換$F$によって「保持」されることで$W^{\prime}$の次元も$n-s$になるという部分が最大のポイントです。

それでは，証明を始めます。はじめに，例外的なケースを除外しましょう。$F$が零写像，すなわち全ての像が$0$となるとき，$W^{\prime}=\{0\}$となり，核の定義より$V^{\prime}=V$となります。このとき，式($\ref{主題}$)は成り立ちます。したがって，以下では$F$が零写像以外のケースを考えます。

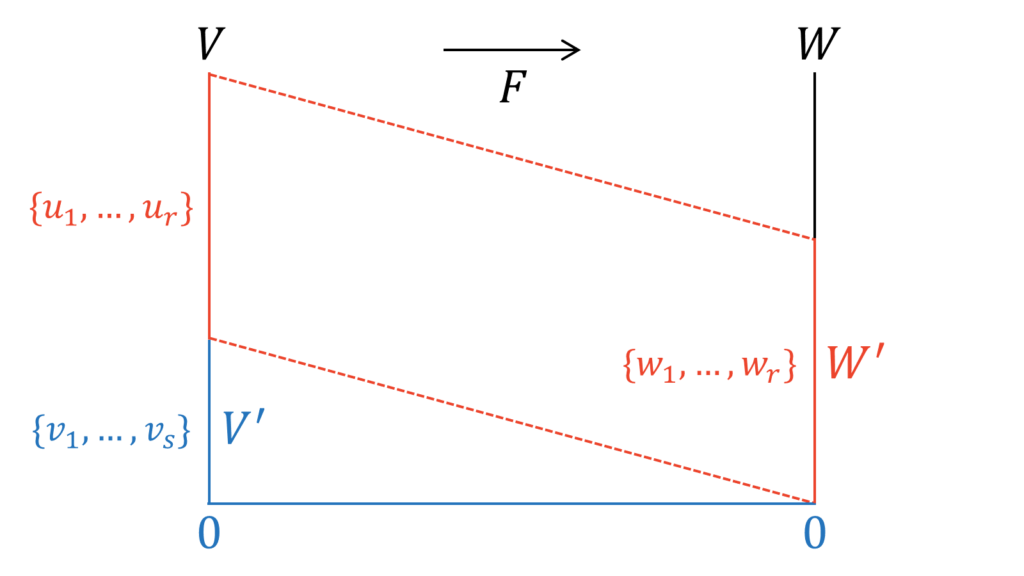
上図のように，$V^{\prime}$の一つの基底を$\vv=\{v_{1},\ldots,v_{s}\}$とします。すると，一次独立な元の集合と基底より，$V^{\prime}$の基底に$V$の元を加えることで$V$の残りの基底を作ることができるため，それらを$\vu=\{u_{1},\ldots,u_{r}\}$とおきます。ただし，$r=n-s$となります。さらに，$\vu$の$F$による像$F(\vu)$を$\vw=\{w_{1},\ldots,w_{r}\}$とおきます。いま，我々が示したいのは，$\vu$の次元と$\vw$の次元が等しくなることです。なぜなら，これらが等しくなること，すなわち$\dim W^{\prime}=r$となることで，

となり，式($\ref{主題}$)を示すことができるからです。したがって，以下では$\vu$の次元と$\vw$の次元が等しくなることを示します。基底の定義より，$\vu$の次元は$r$です。一方，現時点では$\vw$は$W^{\prime}$の基底となるとは限らないため，$\vw$の次元は$r$以下の値となります。逆に言えば，$\vw$が$W^{\prime}$の基底であることを示すことができれば，$\vw$の次元は$r$となり，式($\ref{主題}$)を示すことができます。したがって，以下では$\vw$が$W^{\prime}$の基底であることを示します。改めて基底の定義を再掲すると，$\vw$が以下を満たすことを示せばよいことになります。

まずは，$W^{\prime}$の任意の元が$\vw$の一次結合で表されることを示します。先ほど，$\vv$を拡張して$V$の基底$\vu$を作ったことに注意すると，任意の実数$a_{1},\ldots,a_{s}$と$b_{1},\ldots,b_{r}$に対し，$V$の任意の元$v$は$\vv$と$\vu$の一次結合で表されます。

このとき，$v$の$F$による像を考えます。$F$の線型性より，

となります。したがって，$W^{\prime}$の任意の元$F(v)$は$\vw$の一次結合で表されることを示せました。次に，$\vw$が一次独立であることを示します。いま，実数$c_{1},\ldots,c_{r}$に対し

を考えます。このとき，$\vc$が全て$0$となることを示すことが目標です。$F$の線形性より，式($\ref{一次独立}$)の左辺は

となりますので，式($\ref{一次独立}$)は

と書き換えられます。すなわち，$c_{1}u_{1}+\cdots+c_{r}u_{r}$は$V$の核$V^{\prime}$に属しますので，実数$d_{1},\ldots,d_{s}$に対し，$\vv$の一次結合で表すことができます。

両辺を整理すると，

となります。$\vv$と$\vu$はすべて一次独立ですので，$d_{1},\ldots,d_{s}$と$c_{1},\ldots,c_{r}$はすべて$0$でなければなりません。したがって，$\vw$は一次独立になります。以上で，$\vw$が$W^{\prime}$の基底であることを示せました。