本記事は「これなら分かる!はじめての数理統計学」シリーズに含まれます。
不適切な内容があれば,記事下のコメント欄またはお問い合わせフォームよりご連絡下さい。
ガンマ分布
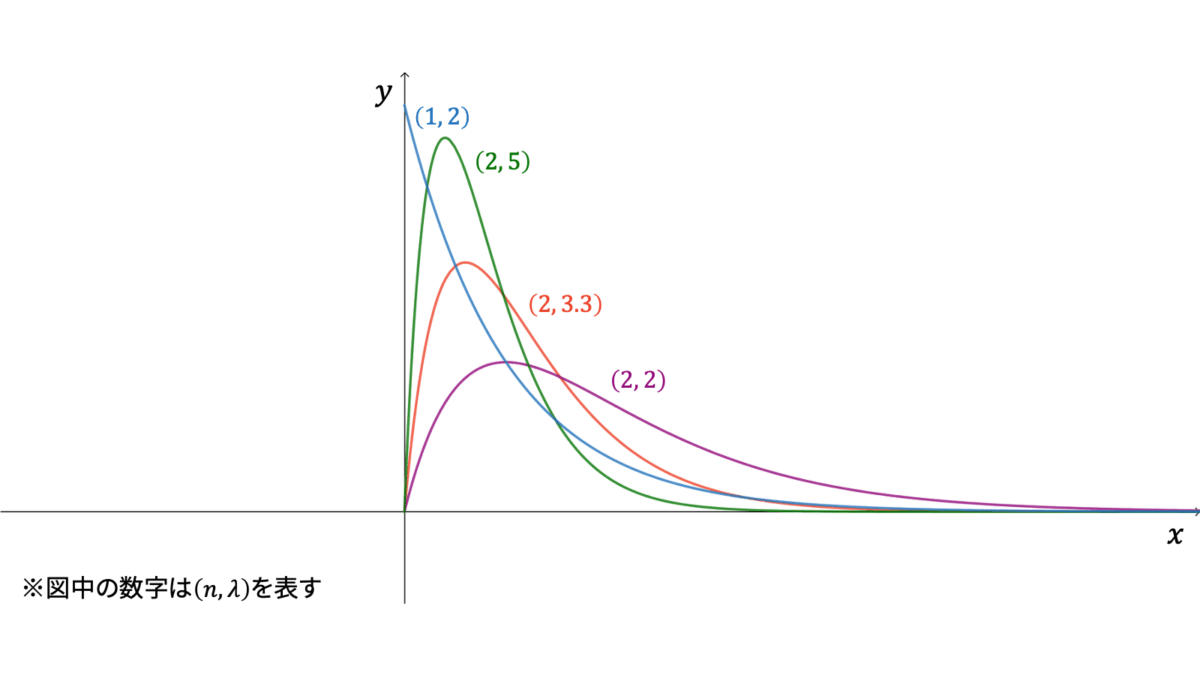
f_{X}(x) &= \frac{\lambda^{n}}{\Gamma(n)}x^{n-1} e^{-\lambda x} \\[0.7em]
M_{X}(t) &= \left( \frac{1}{1-t/\lambda} \right)^{n} \\[0.7em]
E[X] &= \frac{n}{\lambda} \\[0.7em]
V[X] &= \frac{n}{\lambda^2}
\end{align}
ただし,$\Gamma(\cdot)$はガンマ関数を表す。
\Gamma(n) &= \int_0^{\infty}t^{n-1}e^{-t}dt
\end{align}
指数分布に独立に従う確率変数の和が従う分布をガンマ分布と呼び,
\Ga (n, \lambda)
\end{align}
と表します。ただし,$\lambda > 0$とします。ガンマ分布に従う確率変数$X$に対し,実現値は
x \in \bbR_{+}
\end{align}
であり,モーメント母関数の変数は$t < \lambda$とします。ガンマ分布は再生性を持ち,ロードマップ中では指数分布の和に相当すると同時に,負の二項分布の連続拡張に相当します。
確率密度関数
ガンマ分布は,指数分布に独立に従う確率変数の和が従う分布として定義されます。そこで,$X_1, \ldots, X_{n}$がそれぞれ独立に指数分布$\mathrm{Exp}(\lambda)$に従っているとします。すると,$X_1+\ldots+X_{n}$のモーメント母関数は以下のようになります。
M_{X_1+\ldots+X_{n}}(t) &= M_{X_1}(t) \cdots M_{X_{n}}(t) \\[0.7em]
&= \left( 1-\frac{t}{\lambda} \right)^{-n} \\[0.7em]
&= \left( \frac{\lambda}{\lambda-t} \right)^{n} \label{モーメント母関数}
\end{align}
ただし,指数分布のモーメント母関数の条件より$t < \lambda$となります。ガンマ分布の確率密度関数を$f(x)$とおけば,モーメント母関数の定義より以下が成り立ちます。
\int_{0}^{\infty} e^{tx} f(x)dx &= \left( \frac{\lambda}{\lambda-t} \right)^{n} \label{gamma関数の形を定める式}
\end{align}
ここから先の方針は,大きく二つに分かれます。
- 天下り要素が多い方法
- 多変数から一変数への変数変換を用いる方法
天下り要素が多い方法
本パートでは,式($\ref{gamma関数の形を定める式}$)を満たす$f(x)$を天下り的に与え,それがしっかりと式($\ref{gamma関数の形を定める式}$)を満たすことを確認していくという方針を採用します。
この方法は,例えば「ガンマ分布の確率密度関数が$\ldots$で表されることを示せ」という問題に利用することができます。この類の問題ではガンマ分布の確率密度関数が天下り的に与えられていますから,モーメント母関数が式($\ref{gamma関数の形を定める式}$)で表されることを示すだけでOKということです。
かなり天下り的ですが,$f(x)$は以下のような形をしていれば式($\ref{gamma関数の形を定める式}$)を満たすことが知られています。
f(x) &= \frac{\lambda^{n}}{\Gamma(n)}x^{n-1} e^{-\lambda x} \label{ガンマ関数の確率密度関数}
\end{align}
ただし,$\Gamma(\alpha)$はガンマ関数と呼ばれていて,以下のような関数を表します。
\Gamma(n) &= \int_{0}^{\infty} t^{n-1} e^{-t} dt
\end{align}
さて,式($\ref{gamma関数の形を定める式}$)に式($\ref{ガンマ関数の確率密度関数}$)を代入してみましょう。
\int_{0}^{\infty} e^{tx} f(x)dx
&= \int_{0}^{\infty} e^{tx} \frac{\lambda^{n}}{\Gamma(n)} x^{n-1} e^{-\lambda x} dx \\[0.7em]
&= \frac{\lambda^{n}}{\Gamma(n)} \int_{0}^{\infty} x^{n-1} e^{-(\lambda-t)x} dx \label{変換前}
\end{align}
私たちの目標は,式($\ref{変換前}$)を計算して,ガンマ関数のモーメント母関数($\ref{モーメント母関数}$)と等しくなることを示すことです。積分の外側にガンマ関数が出現していますので,積分自体をガンマ関数で表すことを考えます。積分をガンマ関数の形に近づけるため,
(\lambda-t)x &= \nu
\end{align}
という変数変換を利用します。すると,
dx &= \frac{d\nu}{\lambda-t}
\end{align}
となりますので,式($\ref{変換前}$)は以下のように変形できます。
\frac{\lambda^{n}}{\Gamma(n)} \int_{0}^{\infty} x^{n-1} e^{-(\lambda-t)x} dx
&= \frac{\lambda^{n}}{\Gamma(n)} \int_{0}^{\infty} \left(\frac{\nu}{\lambda-t}\right)^{n-1} e^{-\nu} \left(\frac{d\nu}{\lambda-t}\right) \\[0.7em]
&= \left(\frac{\lambda}{\lambda-t}\right)^n \frac{1}{\Gamma(n)}\int_{0}^{\infty} \nu^{n-1} e^{-\nu} d\nu \\[0.7em]
&= \left(\frac{\lambda}{\lambda-t}\right)^n \frac{1}{\Gamma(n)} \Gamma(n) \\[0.7em]
&= \left(\frac{\lambda}{\lambda-t}\right)^n
\end{align}
以上から,$f(x)$を式($\ref{ガンマ関数の確率密度関数}$)のように定めれば($\ref{gamma関数の形を定める式}$)を満たしますので,ガンマ分布の確率密度関数が$f(x)$であることを示すことができました。
多変数から一変数への変数変換を用いる方法
上記方法は非常に簡潔ではあるものの,天下り要素が強すぎてガンマ関数の形に必然性を持たせられません。そこで,本パートでは実際に$Y=X_1+\ldots+X_n$の積分を実行してあげることで,ガンマ分布の形を導出する方法を採用しましょう。
具体的には,多変数から一変数への変数変換を利用します。今回は,$X$が従う分布として指数分布を用い,関数$g$として単純な和算を採用します。このとき,求める$f$がガンマ分布の確率密度関数になります。
f(y) &=\lambda^{n} \int_{R} \delta(y - x_1-\ldots-x_n)e^{-\lambda\left(x_{1}+\cdots+x_{n}\right)} d x_{1} \cdots d x_{n} \label{多変数から一変数}
\end{align}
ただし,$R$は$x_1,\ldots,x_n$の積分範囲を表します。ここで,$Y=x_1+\ldots+x_n$の関係性に注意すると,変換前の$n$個の変数のうち$n-1$個が定まれば,あと$1$つの変数も定まることが分かります。これはまさにディラックのデルタ関数が担っている制約そのものですから,$n-1$個の変数$x_2,\ldots,x_n$に関する積分を扱えば,式($\ref{多変数から一変数}$)からディラックのデルタ関数を取り除くことができます。同時に,ディラックのデルタ関数の制約より$x_1+\ldots +x_n$は必ず$y$と等しくなりますので,$y$と置き変えなくてはならないことに注意して下さい。
f(y) &= \lambda^{n}e^{-\lambda y} \int_{R} d x_{2} \cdots d x_{n} \label{ガンマ分布の積分計算}
\end{align}
ただし,$R$は$x_2,\ldots,x_n$の積分範囲を表します。$x_2$は指数分布に従っているため$x_2 \geq 0$となることに注意すると,
x_2 &= y - (x_3 + \ldots + x_{n}) \\[0.7em]
&\geq 0
\end{align}
が成り立ちます。したがって,$x_3$に関する条件として,
x_3 &\leq y - (x_4 + \ldots + x_{n})
\end{align}
が得られます。同様の変形を$x_4,\ldots,x_n$に適用していくことで,式(\ref{ガンマ分布の積分計算})は以下のように各変数に関する積分に分けることができます。
f(y)
&=\lambda^{n} e^{-\lambda y} \int_{0}^{y} d x_{n}\int_{0}^{y-x_n}dx_{n-1} \cdots \int_{0}^{y-(x_{3}+\cdots+x_{n})} d x_{2}
\label{バラした後のガンマ分布の積分}
\end{align}
式(\ref{バラした後のガンマ分布の積分})を計算していきましょう。一番右側の積分から注目していきます。
\int_{0}^{y-\left(x_{3}+\cdots+x_{n}\right)} d x_{2}=\left\{y-\left(x_{4}+\cdots+x_{n}\right)\right\}-x_{3}
\end{align}
この結果をすぐ左側の積分の中身に移動させます。
&\int_{0}^{y-\left(x_{4}+\cdots+x_{n}\right)}\left[\left\{y-\left(x_{4}+\cdots+x_{n}\right)\right\}-x_{3}\right] d x_{3} \notag \\[0.7em]
&= \left\{y-\left(x_{4}+\cdots+x_{n}\right)\right\}^{2} - \frac{1}{2}\left\{y-\left(x_{4}+\cdots+x_{n}\right)\right\}^{2} \\[0.7em]
&=\frac{1}{2}\left\{y-\left(x_{4}+\cdots+x_{n}\right)\right\}^{2} \\[0.7em]
&=\frac{1}{2}\left[\left\{y-\left(x_{5}+\cdots+x_{n}\right)\right\}-x_{4}\right]^{2}
\end{align}
これを次々に計算していくと,最終的に以下の積分を得ます。
\frac{1}{(n-2)!} \int_{0}^{y}\left(y-x_{n}\right)^{n-2} d x_{n}
&=\frac{1}{(n-1)!}\left[-\left(y-x_{n}\right)^{n-1}\right]_{0}^{y} \\[0.7em]
&=\frac{1}{(n-1)!} y^{n-1}
\end{align}
したがって,ガンマ分布の確率密度関数$f(x)$は以下のようになります。
f(y) &= \frac{\lambda^{n}}{(n-1) !} y^{n-1} e^{-\lambda y}
\end{align}
階乗の一般化としてのガンマ関数$(n-1)!=\Gamma(n)$を用いれば,ガンマ分布の確率密度関数($\ref{ガンマ関数の確率密度関数}$)を導出することができます。
モーメント母関数
先ほど導出したように,ガンマ分布のモーメント母関数は以下のようになります。
M_{X}(t) &= \left( \frac{\lambda}{\lambda - t} \right)^{n}
\end{align}
ただし,$t<\lambda$の条件下でないとガンマ分布のモーメント母関数は存在しません。なお,モーメント母関数の性質で微分演算を行いやすくするために,ガンマ分布のモーメント母関数として以下の同値な形を採用することもあります。
M_{X}(t) &= \left( \frac{1}{1-t/\lambda} \right)^{n} \\[0.7em]
&= \left( 1-\frac{t}{\lambda} \right)^{-n}
\end{align}
平均・分散
連続分布の平均と分散を求めるためには,モーメント母関数の性質を利用します。まず,原点周りの一次モーメント,すなわち期待値を求めます。
E[X] &= \left.M^{\prime}_{X}(t) \right|_{t=0} \\[0.7em]
&= \left. \frac{n}{\lambda} \left( 1-\frac{t}{\lambda} \right)^{-n-1} \right|_{t=0} \\[0.7em]
&= \frac{n}{\lambda}
\end{align}
続いて,原点周りの二次モーメントを求めます。
E[X^2] &= \left.M^{\prime\prime}_{X}(t) \right|_{t=0} \\[0.7em]
&= \left. \frac{n}{\lambda^2}(n+1) \left( 1-\frac{t}{\lambda} \right)^{-n-2} \right|_{t=0} \\[0.7em]
&= \frac{n}{\lambda^2}(n+1)
\end{align}
最後に,原点周りの一次モーメントと原点周りの二次モーメントから分散を求めます。
V[X]
&= E[X^2] - E[X]^2 \\[0.7em]
&= \frac{n}{\lambda^2}(n + 1) - \frac{n^2}{\lambda^2}\\[0.7em]
&= \frac{n}{\lambda^2}
\end{align}
再生性
再生性を示すためには,再生性を示したい分布に従う独立な二つの確率変数を考え,その和のモーメント母関数を計算したときに,パラメータが和の形になっていることを示します。いま,二つの独立な確率変数
X &\sim \Ga (n_x, \lambda) \\[0.7em]
Y &\sim \Ga (n_y, \lambda)
\end{align}
を考えます。このとき,$X+Y$のモーメント母関数を考えます。
M_{X+Y}(t) &= M_{X}(t) \cdot M_{Y}(t) \\[0.7em]
&= \left( \frac{\lambda}{\lambda - t} \right)^{n_x}
\cdot \left( \frac{\lambda}{\lambda - t} \right)^{n_y}\\[0.7em]
&= \left( \frac{\lambda}{\lambda - t} \right)^{n_x+n_y}
\end{align}
これは,$X+Y$のモーメント母関数がガンマ分布のモーメント母関数であることを示しています。つまり,
X+Y &\sim \Ga (n_x+n_y, \lambda)
\end{align}
であり,ガンマ分布の再生性を示しています。
ロードマップ
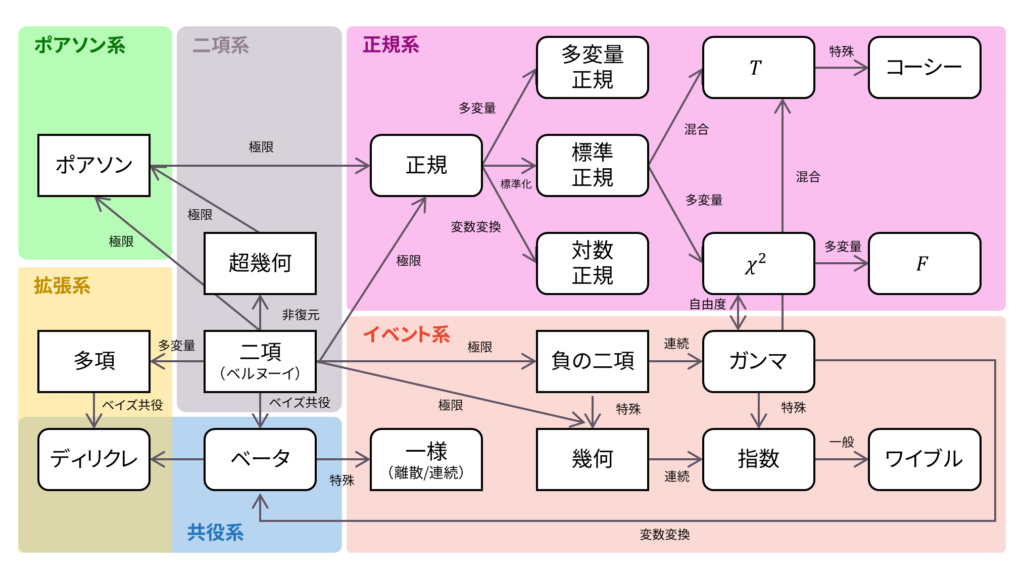
さて,ロードマップに戻りましょう。 ガンマ分布は,指数分布に独立に従う確率変数の和が従う分布として定義されました。確率密度関数の導出方法には,ガンマ分布を天下り的に持ち出す方法と,多変数から一変数への変数変換を用いる方法がありました。ガンマ分布と他の分布の関係性に関しては,以下でまとめています。
参考文献
本稿の執筆にあたり参考にした文献は,以下でリストアップしております。


コメント