【徹底解説】ワイブル分布とは

2023年10月28日

本記事は「これなら分かる！はじめての数理統計学」シリーズに含まれます。

不適切な内容があれば，記事下のコメント欄またはお問い合わせフォームよりご連絡下さい。

ワイブル分布

\begin{align}
f_{X}(x) &= cx^b \exp \left( -\frac{cx^{b+1}}{b+1} \right) \\[0.7em]
E[X] &= m\Gamma(1 + \kappa) \\[0.7em]
V[X] &= m^2 \left\{ \Gamma(1 + 2\kappa)-\Gamma^2(1+\kappa) \right\}
\end{align}

ただし，$\Gamma(\cdot)$はガンマ関数を表し，

\begin{align}
m &= \left( \frac{b+1}{c}\right)^{\kappa},\quad \kappa = (b + 1)^{-1}
\end{align}

と置いた。

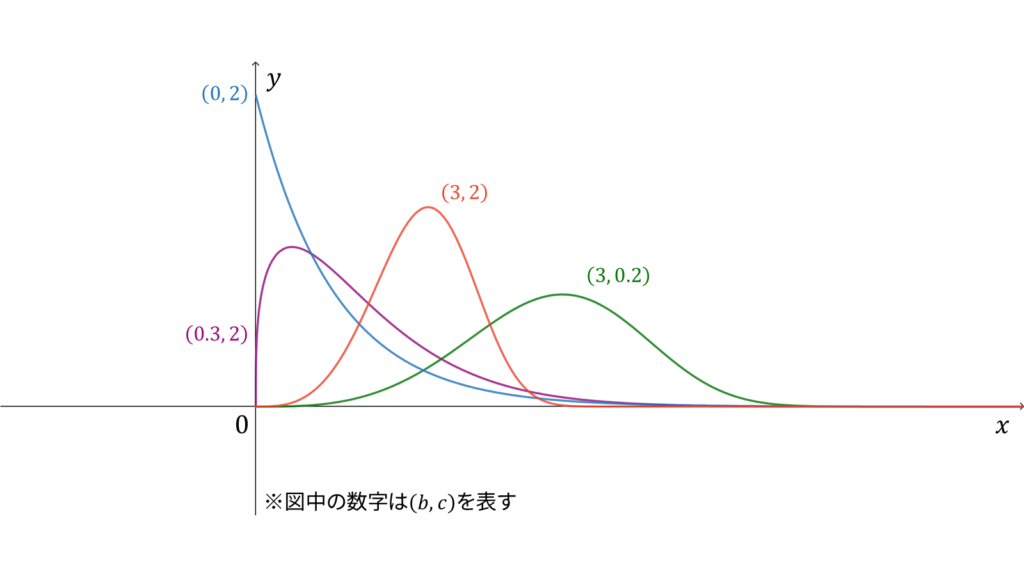
危険率が$ct^b$となる確率分布をワイブル分布と呼びます。他には，以下で導入される確率変数

\begin{align}
Y &= \frac{X^{b+1}}{b+1} \\[0.7em]
&= \kappa X^{\kappa^{-1}}
\end{align}

が指数分布$\Exp (c)$に従うときに，$X$が従う分布がワイブル分布になります。ただし，$\kappa = (b + 1)^{-1}$と置きました。ワイブル分布に従う確率変数$X$に対し，実現値は

\begin{align}
x \in \bbR_{+}
\end{align}

であり，モーメント母関数は$e^x$のテイラー展開とガンマ関数の定義を用いて導出されます。ただし，平均と分散は指数分布からの変数変換を用いて求められますので，今回はモーメント母関数は割愛します。ワイブル分布は再生性を持たず，ロードマップ中では指数分布の一般化に相当します。

確率密度関数

ワイブル分布は，危険率が$ct^b$で与えられる確率分布として定式化されます。危険率に基づく確率密度関数の導出より，危険率を$l(\cdot)$とおくと，確率密度関数$f$は以下のように表されるのでした。

\begin{align}
f(t) &= -\frac{d}{dt} \exp\left(-\int_{0}^{t}l(u)du \right)
\end{align}

証明へ

$l(t)=ct^b$を代入します。

\begin{align}
f(t) &= -\frac{d}{dt} \exp\left(-\int_{0}^{t} cu^b du \right)\\[0.7em]
&= -\frac{d}{dt} \exp\left(- \frac{ct^{b+1}}{b+1} \right)\\[0.7em]
&= ct^b \exp\left(- \frac{ct^{b+1}}{b+1} \right)
\end{align}

モーメント母関数

通常，モーメント母関数を求めるときはモーメント母関数の定義に従って計算していきます。しかし，ワイブル分布の平均と分散は指数分布からの変数変換を用いて求められますので，今回は割愛します。

ワイブル分布のモーメント母関数は$e^x$ののテイラー展開とガンマ関数の定義を用いて導出できます。

平均・分散

通常，連続分布の平均と分散を求めるためには，モーメント母関数の性質を利用します。しかし，ワイブル分布の平均と分散は，指数分布からの変数変換を用いることで簡単に求めることができます。指数分布の確率密度関数とワイブル分布の確率密度関数を見比べると，以下で定義される確率変数

\begin{align}
Y &= \frac{X^{b+1}}{b+1} \label{Y}
\end{align}

が指数分布$\mathrm{Exp}(c)$に従うときに，$X$が従う確率分布がワイブル分布であることが分かります。分かりやすさのため，

\begin{align}
\kappa &= (b+1)^{-1}
\end{align}

と置きましょう。まず，原点周りの一次モーメント，すなわち期待値から求めます。

\begin{align}
E[X]
&= E\left[\left\{ (b+1)Y \right\}^{\kappa}\right]\\[0.7em]
&= (b+1)^{\kappa} E\left[Y^{\kappa}\right]
\end{align}

ただし，式($\ref{Y}$)より，

\begin{align}
X &= \left\{ (b+1)Y \right\}^{\kappa}
\end{align}

を利用しました。$E[Y^{\kappa}]$は，期待値の定義より計算しましょう。

\begin{align}
E[Y^{\kappa}]
&= \int_{0}^{\infty} y^{\kappa} c e^{-cy} dy \\[0.7em]
&= c \int_{0}^{\infty} y^{\kappa} e^{-cy} dy \label{1}\\[0.7em]
&= c \cdot \frac{\Gamma(1+\kappa)}{c^{1+\kappa}} \label{2}\\[0.7em]
&= \frac{\Gamma(1+\kappa)}{c^{\kappa}}
\end{align}

ただし，式($\ref{1}$)から式($\ref{2}$)の変形にはガンマ分布とガンマ関数の関係性を利用しました。したがって，ワイブル分布の期待値は以下のようになります。

\begin{align}
E[X] &= (b+1)^{\kappa} E[Y^{\kappa}] \\[0.7em]
&= \left(\frac{b+1}{c}\right)^{\kappa} \Gamma(1+\kappa)
\end{align}

次に，原点周りの二次モーメントを求めてます。

\begin{align}
E[X^2] &= E\left[\left\{(b+1)Y\right\}^{2\kappa}\right]\\[0.7em]
&= (b+1)^{2\kappa} E[Y^{2\kappa}]
\end{align}

すると，先ほどと同様に

\begin{align}
E\left[Y^{2\kappa}\right]
&= \int_{0}^{\infty} y^{2\kappa} c e^{-cy} dy \\[0.7em]
&= c \int_{0}^{\infty} y^{2\kappa} e^{-cy} dy\\[0.7em]
&= c \cdot \frac{\Gamma(1+2\kappa)}{c^{1+2\kappa}} \\[0.7em]
&= \frac{\Gamma(1+2\kappa)}{c^{2\kappa}}
\end{align}

と計算できますので，原点周りの二次モーメントは以下のように求められます。

\begin{align}
E[X^2] &= \left(\frac{b+1}{c}\right)^{2\kappa} \Gamma(1+2\kappa)
\end{align}

最後に，原点周りの一次モーメントと原点周りの二次モーメントから分散を求めます。

\begin{align}
V[X] &= E[X^2] - E[X]^2 \\[0.7em]
&= \left(\frac{b+1}{c}\right)^{2\kappa} \Gamma(1+2\kappa) - \left(\frac{b+1}{c}\right)^{2\kappa} \Gamma^2(1+\kappa)\\[0.7em]
&= \left(\frac{b+1}{c}\right)^{2\kappa} \left\{\Gamma(1+2\kappa) - \Gamma^2(1+\kappa) \right\}
\end{align}

再生性

再生性を示すためには，再生性を示したい分布に従う独立な二つの確率変数を考え，その和のモーメント母関数を計算したときに，パラメータが和の形になっていることを示します。上でお伝えした通り，ワイブル分布のモーメント母関数は$e^x$のテイラー展開とガンマ関数の積になっています。それゆえ，モーメント母関数の積を考えても同じ関数の形に帰着しないため，ワイブル分布に再生性はありません。

ロードマップ

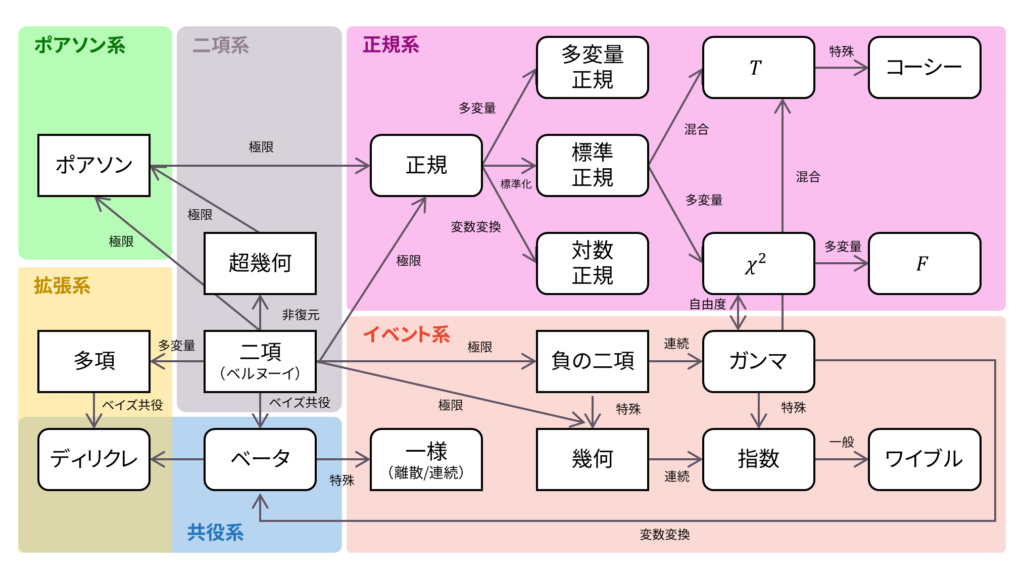
さて，ロードマップに戻りましょう。ワイブル分布は，危険率が$ct^b$となる確率分布として導出されました。また，ワイブル分布と指数分布の確率密度関数を比較することで，$X^{b+1}/(b+1)$が指数分布$\Exp (c)$に従うときに，$X$が従う確率分布としても導出できました。以下の内容も参考になるでしょう。

参考文献

本稿の執筆にあたり参考にした文献は，以下でリストアップしております。

参考文献リストへ

シェアはこちらからお願いします！