本記事は「これなら分かる!はじめての数理統計学」シリーズに含まれます。
不適切な内容があれば,記事下のコメント欄またはお問い合わせフォームよりご連絡下さい。
二項分布
f_{X}(x) &= {}_n C _x~p^x(1-p)^{n-x} \\[0.7em]
G_{X}(s) &= (ps + 1-p)^n \\[0.7em]
E[X] &= np \\[0.7em]
V[X] &= np(1-p)
\end{align}
取り得る結果が成功・失敗の$2$つである独立な試行を繰り返したとき,成功する回数を表す確率分布を二項分布と呼びます。独立なベルヌーイ試行の繰り返しは二項分布に従いますので,独立な確率変数$Y_1,\ldots,Y_n$が$p\in(0,1)$で指定される同一ベルヌーイ分布に従っているとき,確率変数
X &= Y_1+\cdots+Y_n
\end{align}
の従う分布が二項分布であり,
\Bin(n, p)
\end{align}
と書きます。 二項分布に従う確率変数$X$に対し,実現値は
x \in \{0, \ldots, n \}
\end{align}
であり,確率母関数の変数は$|s|\leq 1$とします。二項分布は再生性を持ち,ロードマップ中ではあらゆる分布の出発点に相当します。
確率質量関数
二項分布は,ベルヌーイ試行を$n$回繰り返すことを考えます。$n$回のコイントスのうち表の出る回数を$x$と置けば,二項分布$\Bin (n,p)$の確率質量関数は自然に導かれます。
f_{X}(x) &= {}_n C_x~p^x(1-p)^{n-x}
\end{align}
確率母関数
確率母関数の定義に従って計算していきます。ベルヌーイ分布の確率母関数を利用します。
G_{X}(s) &= E[s^{x}] \\[0.7em]
&= E[s^{(y_1 + \cdots + y_n)}] \\[0.7em]
&= E[s^{y_1}] \cdots E[s^{y_n}] \\[0.7em]
&= (ps + 1-p)^n
\end{align}
平均・分散
離散分布の平均と分散を求めるためには,確率母関数の性質を利用します。まず,確率母関数の一階微分から$E[X]$を求めます。
E[X] &= \left.\frac{d G_{X}(s)}{d s}\right|_{s=1}\\[0.7em]
&= \left. n(ps + 1-p)^{n-1}\cdot p \right|_{s=1}\\[0.7em]
&= np
\end{align}
次に,確率母関数の二階微分から$E[X(X-1)]$を求めます。
E[X(X-1)] &= \left.\frac{d^2 G_{X}(s)}{d s^2}\right|_{s=1}\\[0.7em]
&= \left. n(n-1)(ps + 1-p)\cdot p^2 \right|_{s=1}\\[0.7em]
&= n(n-1)p^2
\end{align}
最後に,分散の定義から分散を求めます。
V[X] &= E[X^2]-E[X]^2\\[0.7em]
&= E[X(X-1)] + E[X]-E[X]^2\\[0.7em]
&= n(n-1)p^2 + np-(np)^2\\[0.7em]
&= np(1-p)
\end{align}
再生性
再生性を示すためには,再生性を示したい分布に従う独立な二つの確率変数を考え,その和の確率母関数を計算したときに,パラメータが和の形になっていることを示します。いま,二つの独立な確率変数
X &\sim \Bin (n, p) \\[0.7em]
Y &\sim \Bin (m, p)
\end{align}
を考えます。このとき,$X+Y$の確率母関数を計算します。
G_{X+Y}(s) &= G_X(s) \cdot G_Y(s) \\[0.7em]
&= (ps + 1-p)^n \cdot (ps + 1-p)^m \\[0.7em]
&= (ps + 1-p)^{n+m}
\end{align}
これは,$X+Y$の確率母関数が$B(n+m, p)$の母関数であることを示しています。つまり,
X+Y \sim \Bin (n+m, p)
\end{align}
であり,二項分布の再生性を示しています。
ロードマップ
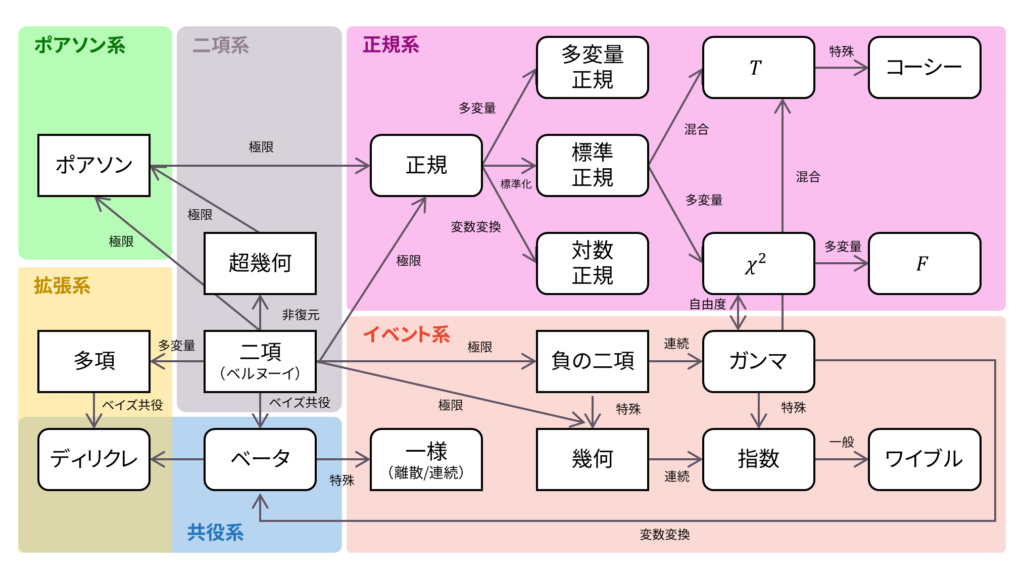
さて,ロードマップに戻りましょう。 二項分布はあらゆる分布の出発点ですので,しっかりとおさえておきたいです。以下の内容も参考になるでしょう。
参考文献
本稿の執筆にあたり参考にした文献は,以下でリストアップしております。


コメント
コメント一覧 (2件)
二項分布の確率質量関数(1)(8)式で、
(1-p) の n-x 乗と思うのですが、違いますでしょうか?
うえうえ様
ご指摘誠にありがとうございます。致命的な誤植でしたので,非常に助かります。本文を修正致しました。