本記事は「これなら分かる！はじめての数理統計学」シリーズに含まれます。
不適切な内容があれば，記事下のコメント欄またはお問い合わせフォームよりご連絡下さい。
コーシー分布の特性関数
コーシー分布の特性関数は，以下で表される。
\phi_X(t) &= e^{-|t|}
\end{align}
コーシー分布のモーメント母関数は存在しませんが，特性関数は存在します。それゆえ，実数領域で定義される期待値と分散は定義されませんが，算術平均に関して再生性を持つという不思議な性質を持ちます。
証明
特性関数の定義より，コーシー分布の特性関数は以下のように計算されます。
\phi_X(t) &= \int_{-\infty}^{\infty}e^{itx}\frac{1}{\pi}\frac{1}{x^2+1} dx \label{特性関数}
\end{align}
式($\ref{特性関数}$)は，複素平面上の積分です。複素関数論の世界では，複素平面上の積分は周回積分を用いて計算します。周回積分というのは，語弊に恐れずに言えば，積分領域が複素平面上において一周するような積分のことを指します。なぜ周回積分を利用するのかというと，後述する孤立特異点を含む周回積分には，以下の留数定理という非常に便利な定理を利用することができるからです。
閉曲線$C$と，$C$が囲む領域$D$を考える。$D$上で定義される関数$f(z)$が$D$内に孤立特異点$a_1, \ldots, a_n$をもち，それ以外で正則であるなら，
\oint_{C} f(z) d z=2 \pi i \sum_{i=1}^{n} \Res_{z=a_{i}} f(z)
\end{align}
が成り立つ。ただし，積分は$C$を反時計回りに進む方向に計算する。
いくつか未知語が出てきましたね。孤立特異点というのは，$f(z)$が正則でない点，つまり例えば$f(z)$が分数の場合に分母が$0$になるような$z$の値のことを指します。$\Res$というのは，以下で定義される留数を表します。
$f(z)$を孤立点$z=a$のまわりにローラン展開（テーラー展開の一般形）したときの$1/(z-a)$の係数を留数と呼び，$\mathrm{Res}_{z=a}f(z)$と書く。孤立点が一位の極のときは，留数は以下のように求められる。
\mathrm{Res}_{z=a} f(z) &= \lim_{z\rightarrow a}(z-a)f(z)
\end{align}
ただし，一位の極というのは，$f(z)=g(z)/(z-a)^n$における$n$を指す。
今回は孤立点が一位の極の場合のみを扱うため，二位以上の極の場合の求め方は割愛します。さて，準備は整いました。特性関数の積分の中身の関数を改めて$g(z)$とおきます。
\phi_X(t) &= \int_{-\infty}^{\infty}e^{itx}\frac{1}{\pi}\frac{1}{x^2+1} dx\\[0.7em]
&= \int_{-\infty}^{\infty}e^{itx}\frac{1}{\pi}\frac{1}{(x+i)(x-i)} dx\\[0.7em]
&= \int_{-\infty}^{\infty} g(z) dz
\end{align}
$g(z)$の形から，$g(z)$は孤立点$z=i$をもち，一位の極であることが分かります。特性関数の計算を，以下の直線$C_1$と曲線$C_2$で構成される閉曲線$C$に沿って行います。閉曲線の選び方はどのように選んでもよいのですが，$g(z)$の孤立点を含めなくては留数定理を利用することができない点に注意してください。$g(z)$の孤立点を含め，コーシー分布の特性関数の形が得られる閉曲線の中で，一番シンプルなものは以下の閉曲線でしょう。
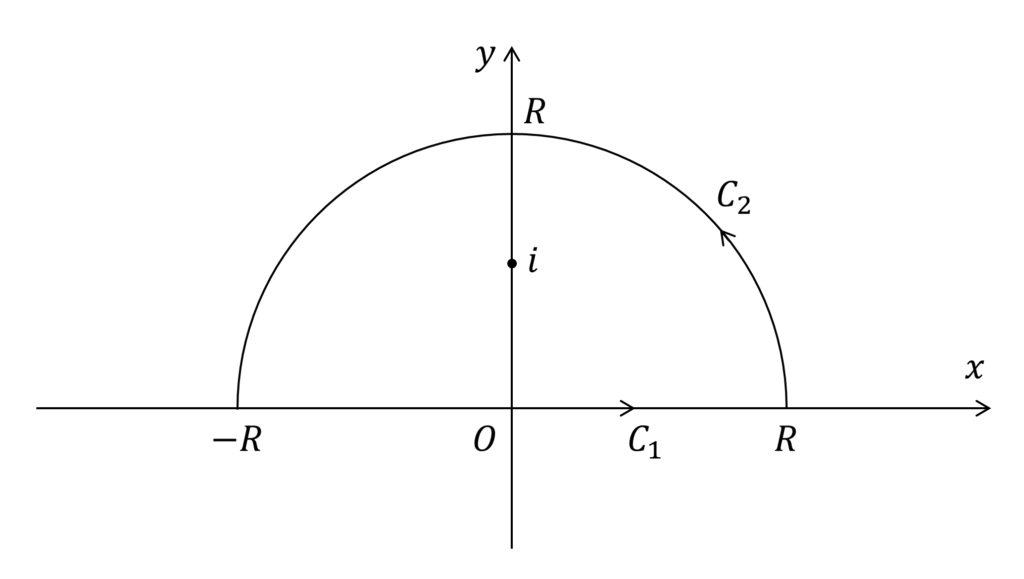
$R\rightarrow \infty$のとき，直線$C_1$に沿った積分が所望の特性関数になっています。$C_2$に沿った積分が$0$に収束することを示します。まずは，留数定理より，一周積分の値を求めておきます。
\oint_{C} f(z)dz &= 2\pi i \mathrm{Res}_{z=i}f(z)
\end{align}
$f(z)$は一位の極でしたから，留数は以下のように求められます。
\mathrm{Res}_{z=i}f(z) &= \lim_{z\rightarrow i}(z-i)f(z) \\[0.7em]
&= \frac{e^{-t}}{2\pi i}
\end{align}
したがって，一周積分は以下の値になります。
\oint_{C} f(z)dz &= e^{-t}
\end{align}
さて，一周積分を2つの積分に分解した後に，$R\rightarrow \infty$の極限をとりましょう。
\lim_{R\rightarrow \infty}\oint_{C} f(z)dz
&= \lim_{R\rightarrow \infty} \left(\int_{C_1} f(z)dz + \int_{C_2} f(z)dz \right)\\[0.7em]
&=\lim_{R\rightarrow \infty} \int_{-R}^{R} f(z)dz + \lim_{R\rightarrow \infty}\int_{C_2} f(z)dz
\end{align}
先ほどもお伝えした通り，第一項目は特性関数そのものです。そこで，第二項目の絶対値に関して不等式を用いることで，上から抑えて収束性を示したいと思います。曲線$C_2$は極座標表示で$z=Re^{i\theta}$かつ$0\leq\theta\leq\pi$と表せます。すると，第二項目の極限の中身は以下のように表されます。
\int_{C_2} f(z)dz
&= \int_0^{\pi}\frac{e^{itRe^{i\theta}}}{\pi (R^2e^{2i\theta}+1)} iRe^{i\theta}d\theta
\end{align}
ここで，$e^{itRe^{i\theta}}$に関する評価を行います。オイラーの公式$e^{i\theta}=\cos\theta + i\sin\theta$を用います。
e^{itRe^{i\theta}}
&= e^{itR(\cos\theta + i\sin\theta)}\\[0.7em]
&= e^{itR\cos\theta} + e^{-tR\sin\theta}\\[0.7em]
&\leq e^{-tR\sin\theta}
\end{align}
ただし，$e^{itR\cos\theta} \geq 0$であることを利用しました。十分大きい$R$に対して
|R^2e^{2i\theta}+1| &\geq R^2+1
\end{align}
となることに注意すれば，第二項目の絶対値は以下のように評価されます。
\left|\int_{C_2} g(z) d z\right| &=\left|\int_{0}^{\pi} \frac{e^{i t R e^{i \theta}}}{\pi\left(R^{2} e^{2 i \theta}+1\right)} i R e^{i \theta} d \theta\right| \\[0.7em]
& \leq \int_{0}^{\pi}\left|\frac{e^{i t R e^{i \theta}}}{\pi\left(R^{2} e^{2 i \theta}+1\right)} i R e^{i \theta}\right| d \theta \\[0.7em]
& \leq \int_{0}^{\pi} \frac{e^{-R t \sin \theta}}{\pi(R^{2}+1)} R d \theta \\[0.7em]
& \leq \frac{R}{\pi\left(R^{2}+1\right)} \int_{0}^{\pi} e^{-R t \sin \theta} d \theta \label{評価後}
\end{align}
式($\ref{評価後}$)を計算するため，指数部の符号で場合分けをします。$t>0$のときを先に考えます。$R>0$に注意すれば，$e^{-R t \sin \theta}\leq 1$より，
\lim_{R\rightarrow \infty}\left|\int_{C_2} g(z) d z\right|
&\leq \lim_{R\rightarrow \infty} \frac{R}{R^2-1}
\rightarrow 0
\end{align}
となります。したがって，$t>0$のときは
\phi_X(t) &= e^{-t}
\end{align}
となります。$t\leq0$のときは，特性関数の以下の性質を利用します。
特性関数の複素共役を利用すると，以下が成り立つ。
\overline{\phi_X(-t)}
&= \overline{E[e^{-itX}]} \\[0.7em]
&= E\left[\overline{e^{-itX}}\right] \notag \\[0.7em]
&= E\left[e^{itX}\right] \\[0.7em]
&= \phi_X(t) \label{特性関数の複素共役}
\end{align}
すると，
\phi_X(t) &= \overline{\phi_X(-t)} \\[0.7em]
&= \overline{e^{-(-t)}} \\[0.7em]
&= e^t
\end{align}
となります。以上をまとめると，コーシー分布の特性関数は以下のようになります。
\phi_X(t) &= e^{-|t|}
\end{align}
参考文献
本稿の執筆にあたり参考にした文献は，以下でリストアップしております。
コメント
コメント一覧 （2件）
式(16)と
(17)から(18)のしたがってが文脈的におかしい気がする
ご指摘ありがとうございます。修正前でも日本語としては正しいと思いますが、「したがって」を削除しました。