本記事は「これなら分かる!はじめての数理統計学」シリーズに含まれます。
不適切な内容があれば,記事下のコメント欄またはお問い合わせフォームよりご連絡下さい。
母関数と確率分布の一意性
$\bbR$上の確率密度関数$f$とその特性関数$\phi$が以下を満たすとする。
\int_{-\infty}^{\infty} |f(x)| dx < \infty ,\quad \int_{-\infty}^{\infty} |\phi(t)| dt < \infty \label{L1}
\end{align}
このとき,以下が成り立つ。
確率母関数もモーメント母関数も,複素数を導入して特性関数として扱うことで一意性を証明できます。なお,特性関数はフーリエ変換対,モーメント母関数はラプラス変換対の特殊なケースに相当します。
証明
全パターンの一意性証明において共通しているのは,母関数から確率関数を計算する反転公式を求めることで,母関数と確率関数が一対一対応していることを示すという方針です。早速,離散型確率変数の場合と連続型確率変数の場合に分けて証明していきましょう。
離散型確率変数の場合
先に結論からお伝えすると,確率質量関数を$p(\cdot)$とおくと,確率母関数$G_{X}(\cdot)$の反転公式は以下の形になります。
p(k) &= \frac{1}{2\pi} \int_{-\pi}^{\pi} G_{X}(e^{it})e^{-ikt} dt \label{確率母関数の反転公式}
\end{align}
ただし,$k$は整数とします。確率母関数の反転公式が式($\ref{確率母関数の反転公式}$)で表されることを証明していきましょう。確率母関数の変数である$s$を,以下のように複素平面上に拡張します。
s &= e^{it}
= \cos t + i\sin t
\end{align}
ただし,$-\pi \leq t < \pi$とします。
変換後の確率母関数は離散型の特性関数に相当します。
ここで,任意の整数$n$に対して以下が成り立つことに注目します。
\int_{-\pi}^{\pi} e^{int}dt &= \int_{-\pi}^{\pi} \cos nt~dt + i \int_{-\pi}^{\pi}\sin nt~dt \\[0.7em]
&=
\begin{cases}
0 & (n \neq 0) \\[0.7em]
2\pi & (n = 0)
\end{cases}
\end{align}
したがって,以下の計算が成り立ちます。
\frac{1}{2\pi} \int_{-\pi}^{\pi} G_{X}(e^{it}) e^{-ikt} dt
&= \frac{1}{2\pi} \int_{-\pi}^{\pi} \left\{ \sum_{j=0}^{\infty} e^{(j-k)it} p(j) \right\}dt\label{1} \\[0.7em]
&= \frac{1}{2\pi} \sum_{j=0}^{\infty} \left\{ \int_{-\pi}^{\pi} e^{(j-k)it} dt\cdot p(j)\right\} \label{2} \\[0.7em]
&= p(k)
\end{align}
ただし,式($\ref{1}$)から式($\ref{2}$)の変形は,被積分関数が$[-\pi, \pi]$上で連続かつその級数が一様収束していることから各項積分定理を利用しました。
数学的な厳密性を求めだすとキリがないです。ここでは,読者の皆さまが何も考えずに積分と総和を入れ替えないように,各項積分定理を利用する必要があることを明示的に記述しておきました。
以上より,確率母関数の反転公式が式($\ref{確率母関数の反転公式}$)で表されることが分かりました。すなわち,確率母関数と確率質量関数は一対一対応することが示されました。
連続型確率変数の場合
結論からお伝えすると,モーメント母関数の反転公式は以下のように表されます。
f(x) &= \frac{1}{2\pi}\int_{-\infty}^{\infty} M_{X}(\theta) e^{-\theta x} d\theta \label{モーメント母関数の反転公式}
\end{align}
特性関数の反転公式は以下のように表されます。
f(x) &= \frac{1}{2\pi}\int_{-\infty}^{\infty} \phi(t) e^{-itx} dt \label{特性関数の反転公式}
\end{align}
式($\ref{特性関数の反転公式}$)は式($\ref{確率母関数の反転公式}$)の連続拡張になっています。これは,モーメント母関数が確率母関数の連続拡張であることからも妥当な結果です。また,式($\ref{モーメント母関数の反転公式}$)と式($\ref{特性関数の反転公式}$)が非常に似ていることが分かります。実は,これらはフーリエ変換対とラプラス変換対に相当します。
本稿では「フーリエ変換対」と「ラプラス変換対」という言葉を利用します。そこまで一般的な言葉ではありませんが,変換対というのは「ある変換とその逆変換」を指すことにします。フーリエ変換対はフーリエ変換とフーリエ逆変換のセットを指し,ラプラス変換対はラプラス変換とラプラス逆変換を指します。
まずは,フーリエ変換とラプラス変換の関係を確認しておきましょう。
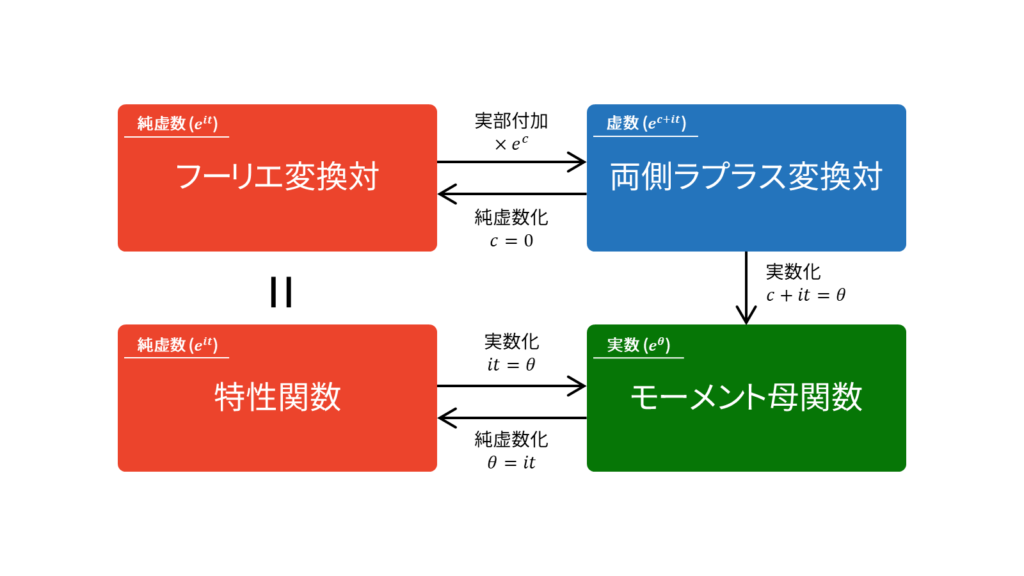
上図のように,フーリエ変換対と特性関数・反転公式は等価になります。両側ラプラス変換対はフーリエ変換対において実部$e^c$を付加したもので,モーメント母関数は両側ラプラス変換対において$(c+it)x$を$\theta x$と置き直して実数化したものになります。具体的には,特性関数・モーメント母関数とその反転公式は以下のように表されます。
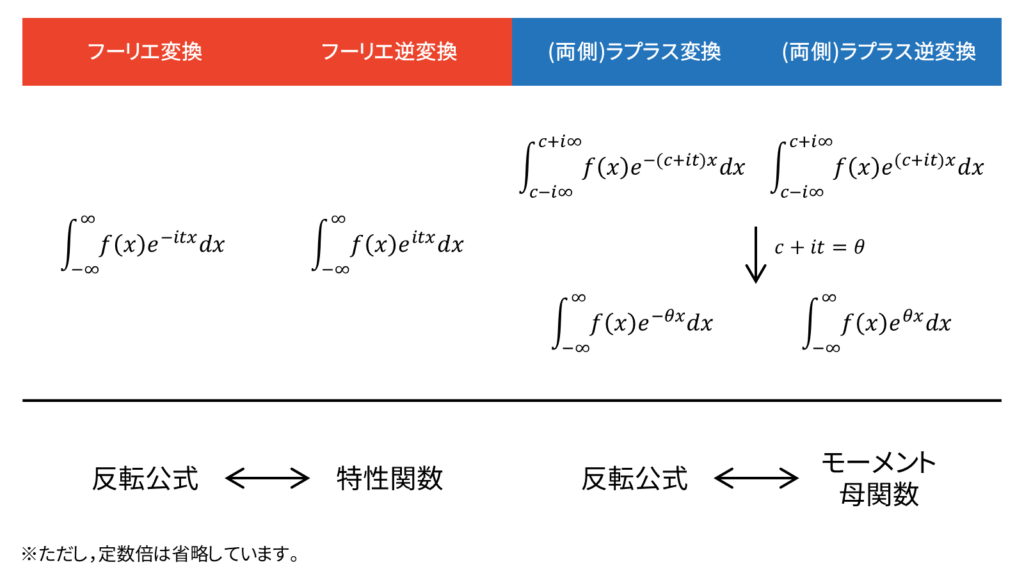
フーリエ変換とラプラス変換には様々な定義の流派がありますが,本稿では上図のように定義することにします。ただし,図中にもある通り,定数倍は省略しています。例えば,ラプラス逆変換では定数倍に虚数が必要ですが,分かりやすさのため省略しています。また,ラプラス逆変換は複素平面上の積分で,一般にブロムウィッチ積分と呼ばれています。
上図を見ると,フーリエ逆変換の定義が特性関数に一致していますので,フーリエ変換が特性関数の反転公式に相当しています。一般に,フーリエ変換対には一意性がありますので,特性関数と確率密度関数は一対一対応していることが分かります。
一方,両側ラプラス逆変換において$(c+it)x$を改めて$\theta x$と置き直すと,定数倍を除いてモーメント母関数の定義と一致します。すると,両側ラプラス変換において$(c+it)x$を改めて$\theta x$と置き直したものがモーメント母関数の反転公式に相当することが分かります。一般に,ラプラス変換対には一意性がありますので,モーメント母関数と確率密度関数は一対一対応していることが分かります。
フーリエ変換とラプラス変換の一意性については,数学的な厳密性を担保した議論が必要になります。少なくとも$L^{p}$空間に対する理解が必要になり,本稿の範囲を超えてしまうためここでは割愛します。
補足
一般には,特性関数が$\bbR$上で定義され,かつ式($\ref{L1}$)を満たすとは限りません。正規分布との畳み込みを用いると,これらの条件を仮定しない状況下において特性関数の一意性を証明することができ,この定理をLévyの反転公式と呼びます。しかし,Lévyの反転公式の証明は本稿の範囲を超えてしまうため,ここでは割愛することにします。
参考文献
本稿の執筆にあたり参考にした文献は,以下でリストアップしております。


コメント
コメント一覧 (2件)
(6)の計算結果は下記ではないでしょうか?
\begin{align}
\int_{-\pi}^{\pi}e^{inx}dx=\frac{2}{n}\sin(n\pi)~(n\neq 0)
\end{align}
ですので、$n≠0$のときゼロにならないと思うのですが、何か見落としあるでしょうか?
ペンネーム様
ご質問ありがとうございます。$\sin(n\pi)$は$n$が整数のときには$0$となることにご注意ください。なお、氏名の本名は編集してコメントを公開しておりますのでご安心ください。