本記事は「これなら分かる!はじめての数理統計学」シリーズに含まれます。
不適切な内容があれば,記事下のコメント欄またはお問い合わせフォームよりご連絡下さい。
F分布
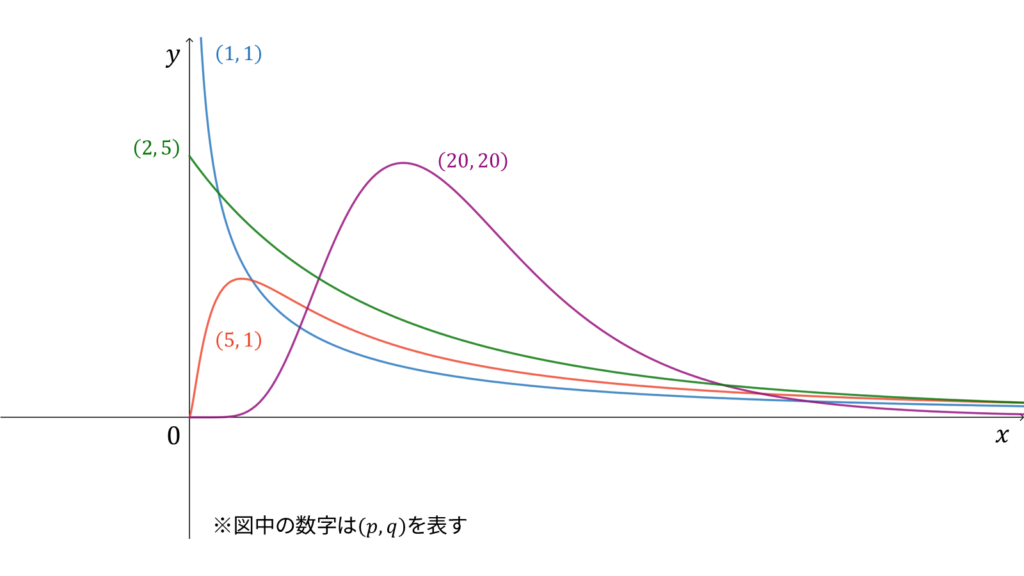
f_{X}(x) &= \frac{p^{p/2}q^{q/2}}{B(p/2, q/2)}\frac{x^{p/2-1}}{(px+q)^{(p+q)/2}} \\[0.7em]
E[X] &= \frac{q}{q-2} \\[0.7em]
V[X] &= 2 \left( \frac{q}{q-2} \right)^2\frac{p+q-2}{p(q-4)}
\end{align}
ただし,$B(\cdot)$はベータ関数を表す。
B(a, b) &= \int_0^1 x^{a-1}(1-x)^{b-1}dx
\end{align}
以下で定義される独立な確率変数
U\sim \chi^2(p) \\[0.7em]
V\sim \chi^2(q)
\end{align}
に対し,確率変数
X &= \frac{U/p}{V/q}
\end{align}
が従う確率分布を自由度$(p,q)$の$F$分布と呼び,
F(p, q)
\end{align}
と表します。$F$分布に従う確率変数$X$に対し,実現値は
x \in \bbR_{+}
\end{align}
であり,モーメント母関数は存在しません。$F$分布は再生性を持たず,ロードマップ中ではカイ二乗分布の多変量化に相当します。
確率密度関数
上で導入した通り,$U$と$V$は互いに独立かつ$U{\sim}\chi^2(p)$,$V{\sim}\chi^2(q)$とします。我々の目標は$(U/p)(V/q)$の従う確率密度関数を求めることですが,一旦定数倍は無視して$Z{=}U/V$の従う確率密度関数を求めましょう。
カイ二乗分布の導出より,$\chi^2(n)$と$\mathrm{Ga}(n/2, 1/2)$は等しくなります。したがって,$U$は$\Ga(p/2,1/2)$に従い,$V$は$\Ga(q/2,1/2)$に従います。一方,ガンマ分布とベータ分布の関係より,二つの独立な確率変数$U{\sim}\Ga(a, c)$と$V{\sim }\Ga(b,c)$に対し,$Y{=}U/(U{+}V)$は$\Be(a, b)$に従うことを利用すると,
Y &\sim \Be\left(\frac{p}{2},~\frac{q}{2}\right)
\end{align}
となります。$Y$と$Z$の定義より$Y{=}Z/(1+Z)$であり,
\frac{dy}{dz} &= \frac{1}{(1+z)^2}
\end{align}
となりますので,$Y$の従う確率分布の確率密度関数を$g$とおくと,$Z$の従う確率密度関数$f$は以下のように表されます。
f(z) &= g(y)\cdot \frac{dy}{dz} \\[0.7em]
&= \frac{1}{B(p/2,~q/2)} \left(\frac{z}{1+z}\right)^{p/2-1}\left(\frac{1}{1+z}\right)^{q/2-1}\cdot\frac{1}{(1+z)^2}\\[0.7em]
&= \frac{1}{B(p/2,~q/2)}\frac{z^{p/2-1}}{(1+z)^{(p+q)/2}}
\end{align}
したがって,先ほどと同様に確率変数の変数変換において確率変数が一つの場合を考えれば,$X=(q/p)Z$の従う確率分布の確率密度関数は,
f(x) &= \frac{1}{B(p/2,~q/2)}\frac{\left\{(p/q)x\right\}^{p/2-1}}{\left\{1+(p/q)x\right\}^{(p+q)/2}}\cdot \frac{dz}{dx} \\[0.7em]
&= \frac{q^{(p+q)/2}\cdot p^{p/2-1}\cdot q^{-p/2+1}}{B(p/2,~q/2)}\frac{x^{p/2-1}}{(px+q)^{(p+q)/2}}\cdot \frac{p}{q} \\[0.7em]
&= \frac{p^{p/2}q^{p/2}}{B(p/2,~q/2)}\frac{x^{p/2-1}}{(px+q)^{(p+q)/2}}
\end{align}
と表されます。
$U$と$V$がどちらも正の値しか取り得ないことから,F分布の実現値も$x>0$となります。
モーメント母関数
F分布のモーメント母関数は存在しません。
平均・分散
連続分布の平均と分散を求めるためには,モーメント母関数の性質を利用します。しかし,F分布にはモーメント母関数が存在しないため,少し工夫して平均と分散の導出を行いましょう。t分布と同様に,先ほど設定した$Y$が$\Be(p/2,q/2)$に従うことを利用しましょう。$Z$の定義に$Z=(p/q)X$を代入すると,
X &= \frac{q}{p}\frac{Y}{1-Y} \label{X}
\end{align}
となります。ここで,ベータ分布の確率密度関数と式($\ref{X}$)の右辺の形が似ていることに注目すると,式($\ref{X}$)より$X$の原点周りの一次モーメント,すなわち平均を計算することは容易であると予想できます。実際に,
E[X] &= \frac{q}{p}E\left[\frac{Y}{1-Y}\right] \\[0.7em]
&= \frac{q}{p}\int_{0}^{1}\frac{y}{1-y}\cdot \frac{1}{B(p/2,~q/2)}y^{p/2-1}(1-y)^{q/2-1} dy \\[0.7em]
&= \frac{q}{p}\cdot\frac{1}{B(p/2,~q/2)}\int_{0}^{1}y^{(p/2+1)-1}(1-y)^{(q/2-1)-1} dy \label{1}\\[0.7em]
&= \frac{q}{p}\cdot\frac{1}{B(p/2,~q/2)}B(p/2+1,~q/2-1) \label{2}\\[0.7em]
&= \frac{q}{p}\cdot\frac{\Gamma(p/2+q/2)}{\Gamma(p/2)\Gamma(q/2)}\frac{\Gamma(p/2+1)\Gamma(q/2-1)}{\Gamma(p/2+q/2)} \\[0.7em]
&= \frac{q}{p}\cdot\frac{p/2}{q/2-1} \\[0.7em]
&= \frac{q}{q-2}
\end{align}
のように$X$の期待値を簡単に計算することができます。ただし,式($\ref{1}$)から式($\ref{2}$)はベータ関数とガンマ関数の関係を利用し,ガンマ関数は正の実数に対して定義されるために$q>2$とします。続いて,原点周りの二次モーメントを求めましょう。原点周りの一次モーメントを求めた際と全く同様の手続きで導出することができます。
E\left[X^2\right] &= \frac{q^2}{p^2}E\left[\frac{Y^2}{(1-Y)^2}\right] \\[0.7em]
&= \frac{q^2}{p^2}\int_{0}^{1}\frac{y^2}{(1-y)^2}\cdot \frac{1}{B(p/2,~q/2)}y^{p/2-1}(1-y)^{q/2-1} dy \\[0.7em]
&= \frac{q^2}{p^2}\cdot\frac{1}{B(p/2,~q/2)}\int_{0}^{1}y^{(p/2+2)-1}(1-y)^{(q/2-2)-1} dy \\[0.7em]
&= \frac{q^2}{p^2}\cdot\frac{1}{B(p/2,~q/2)}B(p/2+2,~q/2-2) \\[0.7em]
&= \frac{q^2}{p^2}\cdot\frac{\Gamma(p/2+q/2)}{\Gamma(p/2)\Gamma(q/2)}\frac{\Gamma(p/2+2)\Gamma(q/2-2)}{\Gamma(p/2+q/2)} \\[0.7em]
&= \frac{q^2}{p^2}\cdot\frac{p/2(p/2+1)}{(q/2-1)(q/2-2)} \\[0.7em]
&= \frac{(p+2)q^2}{p(q-2)(q-4)}
\end{align}
ただし,ガンマ関数は正の実数に対して定義されるため$q>4$とします。したがって,F分布の分散が以下のように求められることが分かりました。
V[X] &= E\left[X^2\right]-E[X]^2 \\[0.7em]
&= \frac{(p+2)q^2}{p(q-2)(q-4)}-\left(\frac{q}{q-2}\right)^2 \\[0.7em]
&= \left( \frac{q}{q-2} \right)^2\cdot\frac{(p+2)(q-2)-p(q-4)}{p(q-4)} \\[0.7em]
&= \left( \frac{q}{q-2} \right)^2\cdot\frac{2(p+q-2)}{p(q-4)} \\[0.7em]
&= 2 \left( \frac{q}{q-2} \right)^2\frac{p+q-2}{p(q-4)}
\end{align}
ガンマ関数が正の実数に対して定義されることから,F分布の平均は$q>2$,分散は$q>4$において定義されることに注意して下さい。
再生性
再生性を示すためには,再生性を示したい分布に従う独立な二つの確率変数を考え,その和のモーメント母関数を計算したときに,パラメータが和の形になっていることを示します。F分布のモーメント母関数は存在せず,特性関数も複雑な形をしており積をとっても同じ関数の形が現れないため,F分布に再生性はありません。
ロードマップ
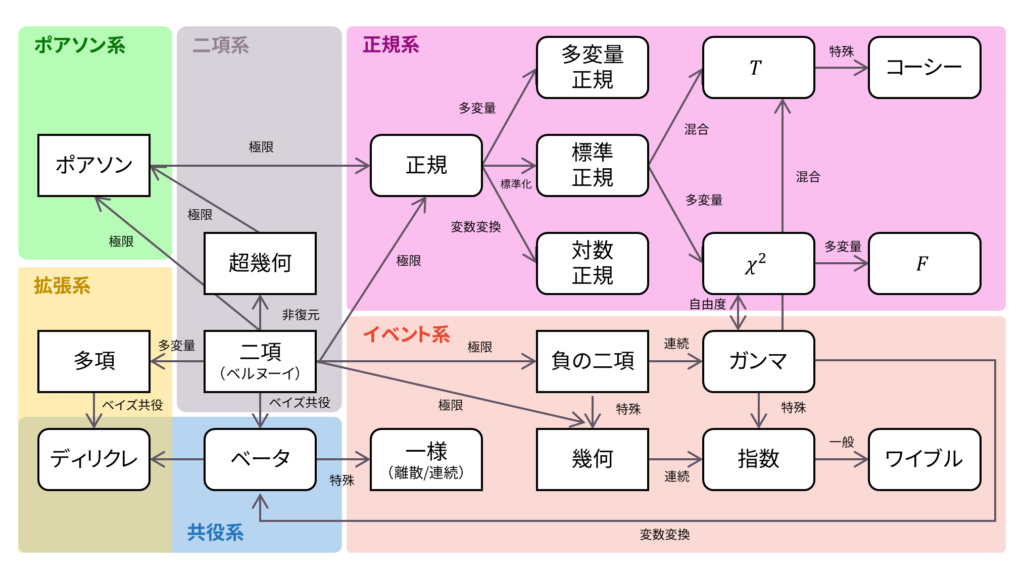
さて,ロードマップに戻りましょう。F分布はカイ二乗分布に従う二つの確率変数の変数変換を用いて導出されました。以下の内容も参考になるでしょう。
- F分布の対称性
- F分布とカイ二乗分布
- F分布とt分布
参考文献
本稿の執筆にあたり参考にした文献は,以下でリストアップしております。


コメント