本記事は機械学習の徹底解説シリーズに含まれます。
初学者の分かりやすさを優先するため,多少正確でない表現が混在することがあります。もし致命的な間違いがあればご指摘いただけると助かります。
はじめに
機械学習を勉強したことのある方であれば,変分ベイズ(VB:variational bayes)の難しさには辟易したことがあるでしょう。私自身,学部生時代に意気揚々と機械学習のバイブルと言われている「パターン認識と機械学習(通称PRML)」を手に取って中身をペラペラめくってみたのですが,あまりの難しさから途方に暮れてしまったことを覚えています。
機械学習の登竜門は,変分ベイズ(変分推論)だと私は考えています。また,VAE(変分オートエンコーダ;variational autoencoder)に代表されるように,変分ベイズは最近の深層学習ブームにおいて理論面の立役者となっている側面もあります。一方で,多くの書籍やWeb上の資料では式変形の行間が詰まっていないことがあるため,初学者は必ず変分ベイズで躓くと言っても過言ではありません。
この問題を解決するため,本稿では変分ベイズをはじめからていねいに説明していきます。具体的には「この解説を読んだだけで変分ベイズの概要と実際の応用方法が理解できる」状態を目指します。多少記事が長くなってしまいますが,ゆっくり自分のペースで読み進めていけば,必ず変分ベイズを理解できるはずです。
一般に,難しい概念を噛み砕いて説明するときには,ボトムアップ的に必要となる知識を武装していく方法と,トップダウン的に求められる知識に寄り道していく方法があります。本稿では,両者を組み合わせて説明していきます。最初に,変分ベイズの目的をお伝えします。その上で,必要となる知識をボトムアップ的に積み上げていくという方針を採用します。
変分ベイズがどのような枠組みで何のために用いられるのかを説明します。
最尤推定・MAP推定・ベイズ推論を実現するための枠組みについて説明します。
混合ガウス分布を例にとってEMアルゴリズムと変分ベイズの使い方を確認します。
pythonを使ってEMアルゴリズムと変分ベイズを実装します。
変分ベイズの目的
本章では,変分ベイズがどのような目的で用いられるのかを説明します。先に結論からお伝えすると,変分ベイズは確率モデルの潜在変数・パラメータに関する事後分布を近似するための手法です。そこで,まず最初に確率モデルと事後分布に関する説明から始めていきます。
確率モデルというのは「現象の裏側に何か適当な分布を仮定する」枠組みのことです。私たちの目的は,ある現象を確率分布を用いて記述することです。そのためには,以下のステップが必要になります。
- ある現象をよく観察して最もよくフィットする既存の確率分布を選択する
- 仮定した確率分布の形状を決定するパラメータを推定する
ある現象に対して既存の分布を仮定するという操作は,観測データの発生方法に対して尤度関数を定めることに相当します。すると,私たちの最終的な目的は分布の形状を決定するパラメータを推定することになります。
尤度関数と同時にパラメータの情報を与える事前分布を設定すると,同時分布を定めることに相当します。ここでは,ある現象に対する既存の分布として尤度関数を定めていますが,ベイズ推定を行う場合には既存の分布として同時分布を定めます。
パラメータの推定方法は,パラメータを1つの値に決め切ってしまう点推定と,パラメータ自体にも既存の分布を仮定するベイズ推定に分けられます。さらに,点推定は尤度関数を最大にする最尤推定と事後確率を最大にする最大事後確率(MAP: maximum a posteriori)推定に分けられます。
- 点推定
- 最尤推定
- MAP推定
- ベイズ推定
以下では,数式を用いて点推定とベイズ推定を説明していきます。
点推定
あるパラメータ$\theta$が与えられたときに,観測データ$X$のふるまいを定義する関数$p(X|\theta)$が尤度関数です。最尤推定では,尤度関数$p(X|\theta)$を最大にする$\theta$の値を求めます。
\hat{\theta}_{\ML} &= \argmaxTheta p(X | \theta)
\end{align}
条件付き確率の定義より,$p(X | \theta)$は「$\theta$が与えられたときの$X$」の確率を表します。言い換えれば「$\theta$が与えられたときに$X$はどれだけ尤もらしいか」を表しています。最尤推定では,条件付けられた$\theta$を変数として読み替えることで,データ$X$に対して最も尤もらしいパラメータ$\theta$を推定します。
$p(X|\theta)$を関数と呼ぶことに違和感がある人は鋭い視点をお持ちです。測度論を用いると,確率は可測空間上の確率測度(つまり関数)として定義されます。測度論を用いない場合の確率$p$の定義は,こちらからご確認ください。
一方で,MAP推定では事後確率$p(\theta|X)$を最大にする$\theta$の値を求めます。
\hat{\theta}_{\MAP} &= \argmaxTheta p(\theta | X) \\[0.7em]
&= \argmaxTheta \frac{p(X | \theta)p(\theta)}{p(X)} \\[0.7em]
&= \argmaxTheta p(X | \theta) p(\theta)
\end{align}
ただし,変形にはベイズの定理を利用しました。$\theta$に関する最大化問題であるため,最終行では$p(X)$を無視しました。
計算を簡単にするため,最尤推定やMAP推定では両辺の対数を取った対数尤度関数や対数事後確率を最大化することが多いです。対数関数は単調増加関数であるため,対数を取る前後の最大最小問題は等価になります。
\hat{\theta}_{\ML} &= \argmaxTheta \ln p(X | \theta) \\[0.7em]
\hat{\theta}_{\MAP} &= \argmaxTheta \left\{ \ln p(X | \theta) + \ln p(\theta) \right\}
\end{align}
確率モデルをうまく設定できれば,これらの点推定は解析的に解くことも可能です。例えば,正規分布の形状を決定する母平均の最尤推定量は標本平均に一致し,母分散の最尤推定量は標本分散に一致します。これらはラグランジュの未定乗数法を用いて証明されます。
ベイズ推定
ベイズ推定では,点推定とは異なりパラメータを値ではなく分布として求めることで,データへの過学習を防止したり,表現力を上げたりすることができます。パラメータの分布というのは,ある観測データ$X$が得られたときの事後分布$p(\theta | X)$のことを表しています。
p(\theta | X) &= \frac{p(X | \theta)p(\theta)}{p(X)}
\end{align}
点推定とは異なり,ベイズ推定では$\arg \max$が付いていませんね。$\arg \max$・$\arg \min$は目的関数が最大・最小になるパラメータを値として求めることを意味しています。耳が痛いようですが,ベイズ推定では仮定した確率分布$p$の形状を決めるパラメータ$\theta$の事後分布$p(\theta | X)$を求めます。
点推定の限界として,対象とする現象が多峰性のふるまいを示しているケースが挙げられます。多峰性とは,複数のピークをもつ性質のことを指します。多峰性の現象に対して点推定を行うと,1つのピーク以外の情報を完全に捨て去ってしまいます。
各種推定方法の実現
本章では,各種パラメータの推定方法がどのように実現されるのかについて説明します。先に結論からお伝えすると,点推定を実現する方法はEMアルゴリズム,ベイズ推定を実現する方法は変分ベイズがよく利用されます。
- 点推定
- EMアルゴリズム
- ベイズ推定
- 変分ベイズ(変分推論)
ちなみに,変分ベイズは文脈によっては「変分推論」とも呼ばれます。ベイズモデリングであることを強調したい場合は「変分ベイズ」と呼ばれることが多いようです。
確率モデルの問題を考えるときには,まず最初に確率モデルに潜在変数$Z$(尤度関数に姿を現さない変数)を導入します。そうすることで,複雑な分布をより単純な分布を使って表すことが可能になります。潜在変数を導入することは,同時分布$p(X,Z)$を設計することに相当します。ここが全ての始まりです。観測データ$X$と潜在変数$Z$にどのような依存関係があるのかを同時分布として設定してしまうわけです。
ベイズ推定では,副次的に尤度関数$p(X|Z)$と事前分布$p(Z)$を仮定することになります。
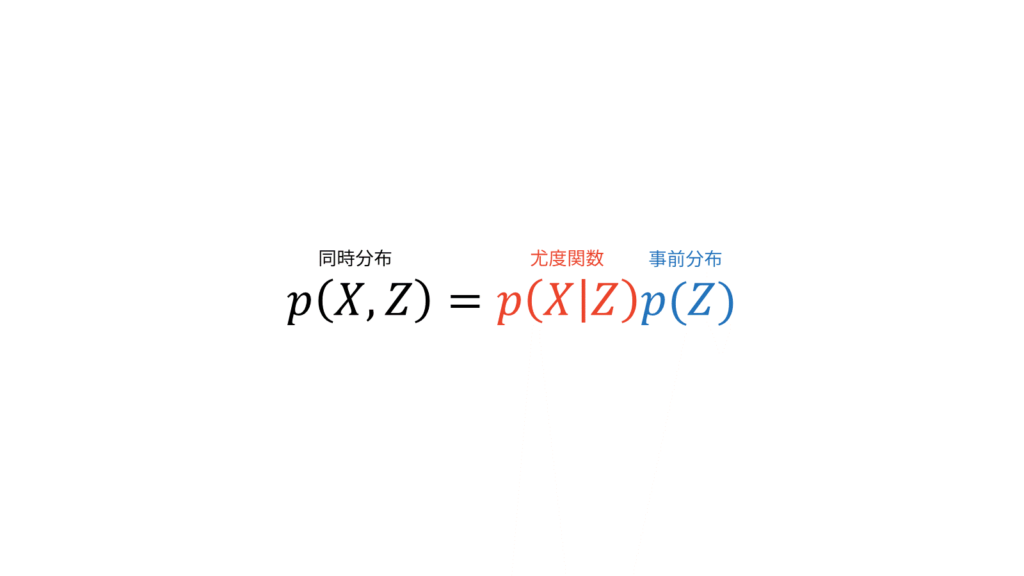
尤度関数と事前分布を定めることは,同時分布を定めることだけでなく,事後分布の形を定めることにも相当します。なぜなら,$X$が観測データであることから$p(X)$は定数だからです。
p(Z|X) &= \frac{p(X, Z)}{p(X)} \\[0.7em]
&\propto p(X, Z) \\[0.7em]
&= p(X|Z)p(Z)
\end{align}
点推定では,事前分布が無情報(定数)だと仮定します。結局,上でお伝えしたように,点推定では同時分布を設計することは尤度関数を設定することに相当します。
p(X, Z) &= p(X|Z)p(Z) \\[0.7em]
&= p(X|Z)\cdot \const \\[0.7em]
&\propto p(X|Z)
\end{align}
ベイズ推定では,事前分布には共役事前分布を仮定するケースが多いです。共役事前分布を設定すると,事後分布は事前分布と同じ形になりますので,圧倒的に計算が簡単になります。一方で,全ての尤度関数に対して共役事前分布が存在する訳ではなく,以下の分布対が利用されることが多いです。
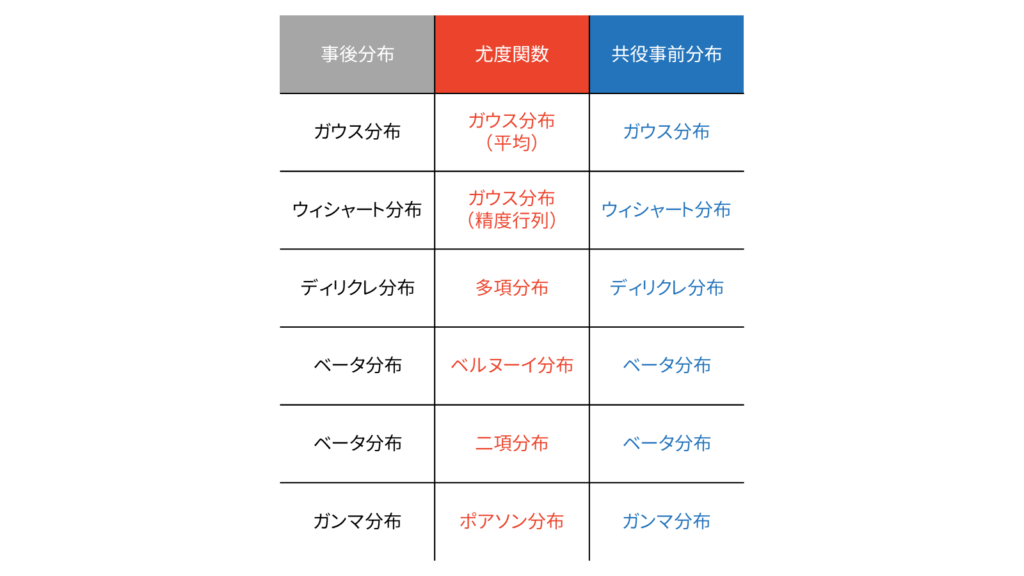
変分ベイズの本領が発揮されるのは,共役事前分布を定められないとき,もしくは事前分布が部分的な共役性しか持たないときです。今回扱う混合ガウス分布も,部分的な共役性をもつ確率モデルの一例ですので,変分ベイズの本領が発揮されることになります。
EMアルゴリズム
結論からお伝えすると,EMアルゴリズムは以下の流れで計算されます。
詳しい導出方法は「EMアルゴリズムをはじめからていねいに」をご参照下さい。
変分ベイズ
変分ベイズの目的は,確率モデルの潜在変数・パラメータに関する事後分布を求めることでした。EMアルゴリズムでは潜在変数を$Z$,パラメータを$\theta$と区別しましたが,変分ベイズでは両者を一括りにして$Z$と表しますので,事後分布は$p(Z|X)$と表されます。EMアルゴリズムでは$p(Z|X)$を計算できるという立場を取りましたが,変分ベイズでは$p(Z|X)$を計算できないという立場を取ります。
変分ベイズは,事後分布$p(Z|X)$を別の新しい分布$q(Z)$で近似してしまおうという大胆かつ汎用性の高い手法です。
q(Z) &\sim p(Z|X)
\end{align}
この出発点こそ,変分ベイズが変分法の一種であることを裏付けています。変分法とは,ある関数の最適化問題を解く手法の一つです。今回は「真の事後分布を別の新しい分布$q(Z)$で近似する」という文脈で変分法を用いています。語弊を恐れずに言うならば,変分法は微分法の拡張です。微分法では$N$次元ユークリッド空間における臨界点(微分が$0$になって関数が平らになる部分)を求めるのに対し,変分法では無限次元関数空間における臨界点を求めます。
結論からお伝えすると,変分ベイズでは以下の更新式を利用して潜在変数・パラメータに関する近似事後分布$q^{\ast}(Z)$を求めます。
\ln q_{i}^{\ast}(Z_i) &= E_{j \neq i} \left[ \ln p(X, Z) \right] + \const \label{eq_vb_update}
\end{align}
$q$と$Z$の添え字である$i$と$j$の意味については後ほどお伝えします。
更新式の導出には2通りの方法があります。1つ目は,事後分布とのKLダイバージェンスを最小化するような分布を求める方法です。2つ目は,EMアルゴリズムと同じ枠組みで周辺対数尤度関数を下限とKLダイバージェンスの2つに分解して考える方法です。前者は直感的に理解しやすい方法であり,後者はEMアルゴリズムと数学的な背景を一貫させて理解することができる方法です。それぞれ詳しく見ていきましょう。
KL最小化による近似
私たちの目的は,$p(Z|X)$をよく近似する$q(Z)$を求めることでした。2つの分布間の距離を測るオーソドックスな指標としては,KLダイバージェンスが利用できます。指標としてKLダイバージェンスを用いる理由は,必然性を理論的に説明できるからです。この必然性については次の「EMアルゴリズムの類推」で説明します。
2つの分布間の距離を測る指標としてKLダイバージェンスを採用することを受け入れると,$p(Z|X)$とのKLダイバージェンスが小さくなるような$q(Z)$を求めれば良いことになります。EMアルゴリズムでは,真の事後分布を計算できるという立場を取るため,KLダイバージェンスを$0$にする近似事後分布を求めることができました。一方で,変分ベイズでは真の事後分布を計算することができないという立場を取るため,近似分布が真の事後分布と厳密に等しくなることはないと仮定します。
しかし,何の制限もない中で$p(Z|X)$とのKLダイバージェンスが小さくなるような$q(Z)$を求めるのは自由度が高すぎて困難です。そこで,変分ベイズでは「平均場近似」と呼ばれる仮定を採用します。
q(Z) &= \prod_{i=1}^{M} q_i (Z_i)
\end{align}
平均場近似は,事後分布$p(Z|X)$をよく近似する$q(Z)$は独立な分布$q_i(Z_i)$の積で表されるという強い仮定を表しています。ただし,必ずしも全ての要素が独立だという仮定ではないことに注意してください。あくまでも,どのような要素に分解するかの「グループ分け」が平均場近似の仮定だと認識しておきましょう。
すると,グループ分けした潜在変数・パラメータのインデックスを$i$とおいたときに,求める$q_i(Z_i)$というのは以下の解になります。ただし,$q_i (Z_i)$のことを$q_i$と省略して書きます。
\argminQi \KL \left. \left[ \prod_{i=1}^M q_i(Z_i) \right\| p(Z|X) \right]
\end{align}
KLダイバージェンスは非対称ですので,$\KL(p\|q)$と$\KL(q\|p)$は異なります。前者をForward KL,後者をReverse KLと呼ぶことがあります。KLダイバージェンスの定義より,Forward KLは$\log$関数を$p$で重みづけしていますので,$p \neq 0$の部分を$q$で網羅しようとします。その結果,$q$の分散は大きくなりやすいです。一方で,Reverse KLは$\log$関数を$q$で重みづけしていますので,$q$は$0$ではない部分で$p$を網羅しようとします。その結果,$q$の分散は小さくなりやすいです。例えば,真の事後分布が多峰性の場合,Forward KLでは複数のピークをならしたような近似事後分布が得られるのに対し,Reverse KLではある1つのピークに着目した近似事後分布が得られやすいです。多峰性の場合は近似事後分布に混合ガウス分布を持ち出せばうまくフィッティングできますが,KLダイバージェンスの非対称性を把握しておくことは非常に大切です。
実際に計算していきます。KLダイバージェンスの定義より,以下のように計算することができます。
q_i(Z_i) &= \argminQi \KL \left. \left[ \prod_{i=1}^M q_i(Z_i) \right\| p(Z|X) \right] \\[0.7em]
&= \argminQi E_{q} \left[ \ln \frac{\prod_{i=1}^M q_i(Z_i)}{p(Z|X)} \right]
\end{align}
今求めたいのは$Z_i$に対する近似事後分布ですので,期待値を取る際には$q_i(Z_i)$に対する期待値と$q_{j \neq i} (Z_{j \neq i})$に対する期待値を分けて考えてあげます。$q_{j \neq i}$は「$i$とは異なる$j$」と読むと理解しやすいです。
q_i(Z_i) &= \argminQi E_{q} \left[ \ln \frac{q_i(Z_i)q_{j \neq i} (Z_{j \neq i})}{p(Z|X)} \right] \\[0.7em]
&= \argminQi E_{q_i} \left[ E_{q_{j \neq i}} \left[ \ln \frac{q_i(Z_i)q_{j \neq i} (Z_{j \neq i})}{p(Z|X)} \right] \right] \\[0.7em]
&= \argminQi \Biggl\{ E_{q_i} \left[ E_{q_{j \neq i}} \left[ \ln q_i(Z_i) \right] + E_{q_{j \neq i}} \left[ \ln q_{j \neq i}(Z_{j \neq i}) \right]-E_{q_{j \neq i}} \left[ \ln p(Z|X) \right] \right] \Biggr\}
\end{align}
$q(Z)$を$i$と$j \neq i$に分けるというアイディアが少し奇抜に感じられるかもしれません。これは後に,KLダイバージェンスを$0$にする$q(Z)$を見つけるための苦肉の策です。平均場近似は強い仮定であることから「各因子ごとであればKLダイバージェンスを$0$にする事後分布を計算できるのではないか」というアイディアに着想した結果です。実際に計算を進めていくと,式($\ref{eq_KL_q_i}$)でKLダイバージェンスを$0$にする$q_i (Z_i)$を導出できることが分かります。
さて,ここで期待値に関する以下の性質を利用します。
- $1$の期待値は$1$
E_{X}[1] &= 1
\end{align}
- 期待値の対象と中身が独立な(定数とみなせる)場合に期待値の外に出せる [参考]
E_{X}[aX + b] &= aE_{X}[X]+b
\end{align}
- 確率変数の過不足なく期待値を取った結果はスカラー
E_{Y}[E_{X}[XY]] = E_{Y}[\mu_xY] = \mu_xE_{Y}[Y] = \mu_x\mu_y
\end{align}
最後の項目について少し補足しておきます。期待値の定義は注目している確率変数に対する周辺化操作に相当しますので,確率変数に過不足なく期待値を取った結果はスカラーになります。
以上を踏まえると,以下が成り立ちます。
E_{q_{j \neq i}} \left[ \ln q_i(Z_i) \right] &= \ln q_i(Z_i) \\[0.7em]
E_{q_{j \neq i}} \left[ \ln q_{j \neq i}(Z_{j \neq i}) \right] &= \const
\end{align}
したがって,先ほどの計算を進めることができます。
q_i(Z_i) &= \argminQi \Biggl\{ E_{q_i} \left[ \ln q_i(Z_i) + \const-E_{q_{j \neq i}} \left[ \ln p(Z|X) \right] \right] \Biggr\} \\[0.7em]
&= \argminQi \Biggl\{ E_{q_i} \left[ \ln q_i(Z_i)-E_{q_{j \neq i}} \left[ \ln p(Z|X) \right] \right] \Biggr\} \\[0.7em]
&= \argminQi \Biggl\{ E_{q_i} \left[ \ln \frac{q_i(Z_i)}{\exp \left( E_{q_{j \neq i}} \left[ \ln p(Z|X) \right] \right) } \right] \Biggr\} \\[0.7em]
&= \argminQi \Biggl\{ E_{q_i} \left[ \ln \frac{q_i(Z_i)}{\exp \left( E_{q_{j \neq i}} \left[ \ln p(Z|X) \right] \right)/C }-\ln C \right] \Biggr\} \\[0.7em]
&= \argminQi \KL \left[ q_i(Z_i) \left\| \frac{ \exp \left( E_{q_{j \neq i}} \left[ \ln p(Z|X) \right] \right)}{C} \right. \right] \label{eq_KL_q_i}
\end{align}
KLダイバージェンスを最小にするのは2つの分布が等しいときですので,結局以下が得られます。
q_i(Z_i) &= \frac{ \exp \left( E_{q_{j \neq i}} \left[ \ln p(Z|X) \right] \right)}{C}
\end{align}
両辺の対数を取ると,冒頭で説明した公式($\ref{eq_vb_update}$)が得られます。
\ln q_i(Z_i) &=E_{q_{j \neq i}} \left[ \ln p(Z|X) \right] + \const \\[0.7em]
&= E_{q_{j \neq i}} \left[ \ln \frac{p(X, Z)}{p(X)} \right] + \const \\[0.7em]
&= E_{q_{j \neq i}} \left[ \ln p(X, Z) \right] + \const
\end{align}
「自分以外全ての潜在変数・パラメータで仮定した確率モデルの期待値を取ると近似事後分布の形が得られる」と理解しましょう。冒頭にもお伝えした通り,我々の目標は得られたデータ$X$の背後に潜む事後分布$p(Z|X)$の形を求めることでした。確率モデルの問題では,確率変数同士の依存関係を同時分布$p(X,Z)$としてこちら側で定めてしまうのでした。ゆえに,式($\ref{eq_vb_update}$)の右辺を計算することができます。
EMアルゴリズムの類推
ここまでの方針は,$p(Z|X)$を良く表す近似事後分布$q(Z)$を,KLダイバージェンスという恣意的な指標を用いて測りました。そこで,ここからはKLダイバージェンスが出てくる必然性を説明していきます。
思い出して欲しいのは,EMアルゴリズムにおける下限の導出過程です。下限と対数尤度関数の差は,KLダイバージェンスの形になりましたね。この経験から類推するに,変分ベイズでも目的関数に対してイェンセンの不等式を適用すれば,KLダイバージェンスが出現するはずです。
さて,変分ベイズの目的関数というのは一体何なのでしょうか。EMアルゴリズムの目的は対数尤度関数の最大化でしたので,目的関数が自明でした。しかし,変分ベイズの目的は事後分布$p$をよく表す近似事後分布$q$を見つけることでしたので,目的関数は自明ではありません。目的ドリブンで考えると,変分ベイズの目的関数が$q$と$p$のKLダイバージェンスになるというのは「距離指標としてKLダイバージェンスを採用する必然性が(今のところ)ないこと」を除いて理にかなっています。
こういうときは,出発点に立ち返ることが大切です。私たちの目的は,ある現象を確率分布を用いて記述することです。そのためには,以下のステップが必要になるのでした。
- ある現象をよく観察して最もよくフィットする既存の確率分布を選択する
- 仮定した確率分布の形状を決定するパラメータを推定する
点推定では「パラメータの値」自体に興味があるため,対数尤度関数をパラメータの関数と読み替えて最大化問題を解きました。その際,潜在変数の出現による和の対数部分が計算困難であるため,イェンセンの不等式を利用して対数尤度関数を下から評価したのでした。
\ln p(X | \theta) &= \calL_{\ML} \left[ q(Z), \theta \right] + \KL \left. \left[ q(Z) \right\| p(Z|X, \theta) \right] \label{eq_EM}
\end{align}
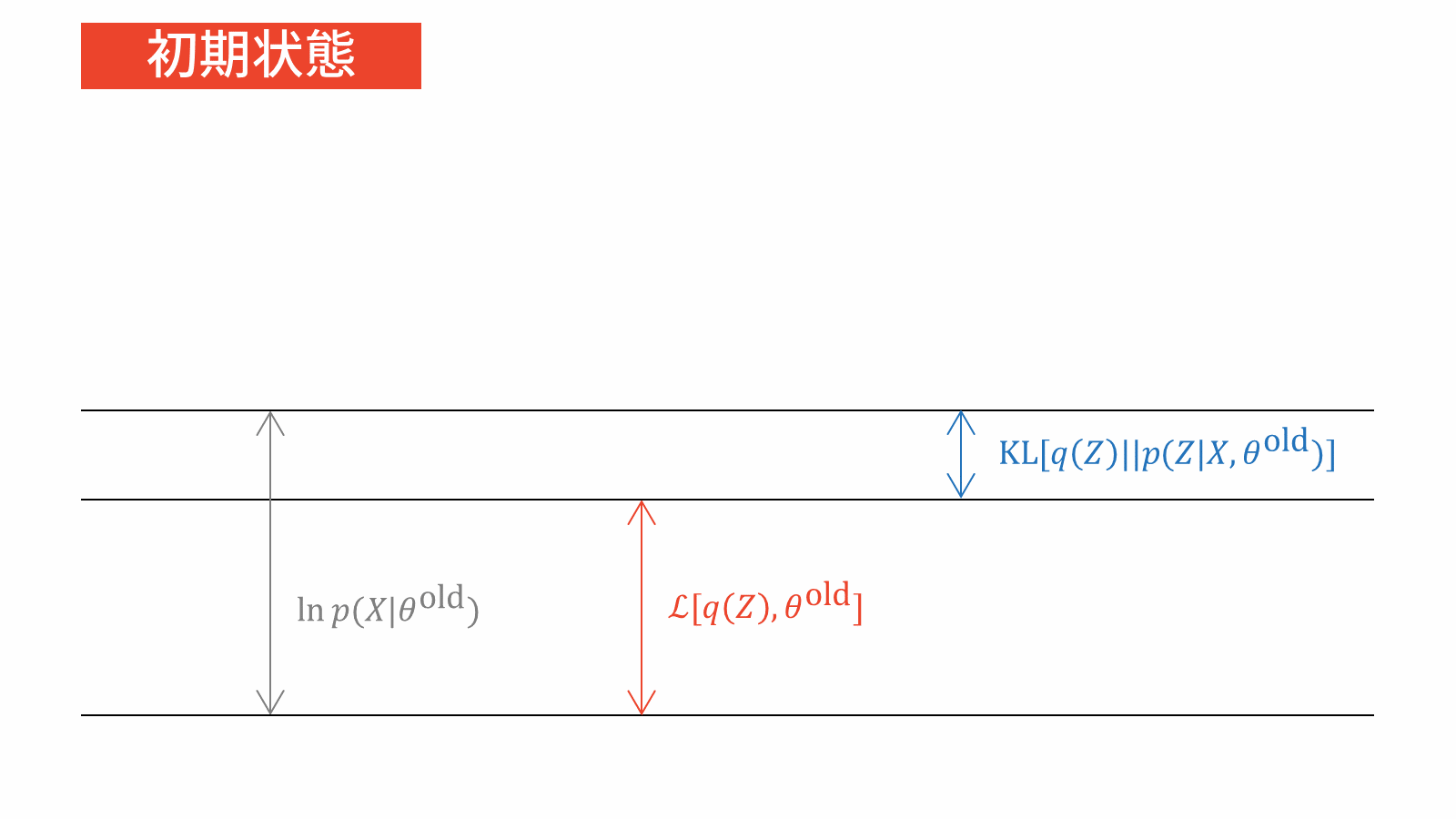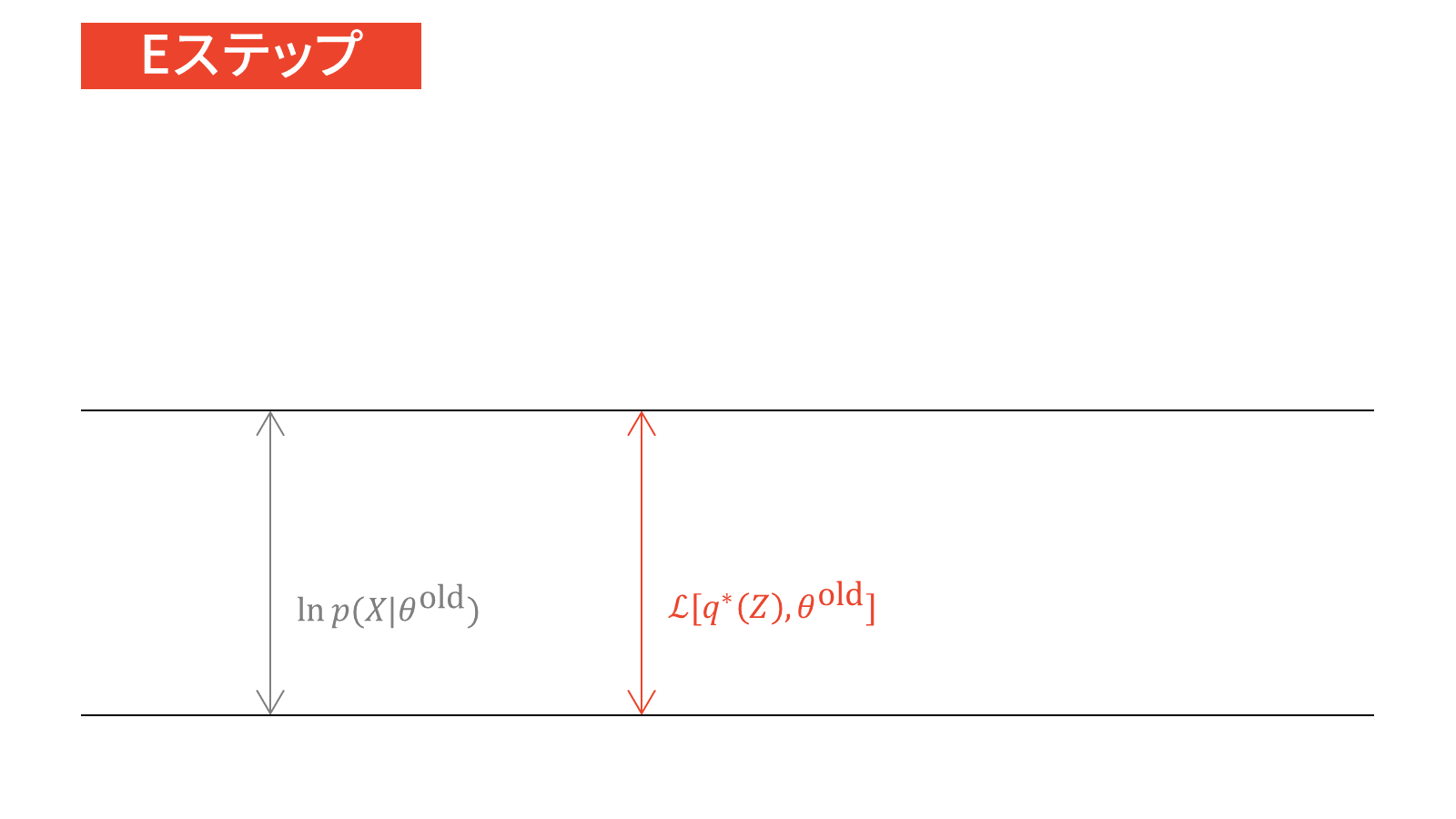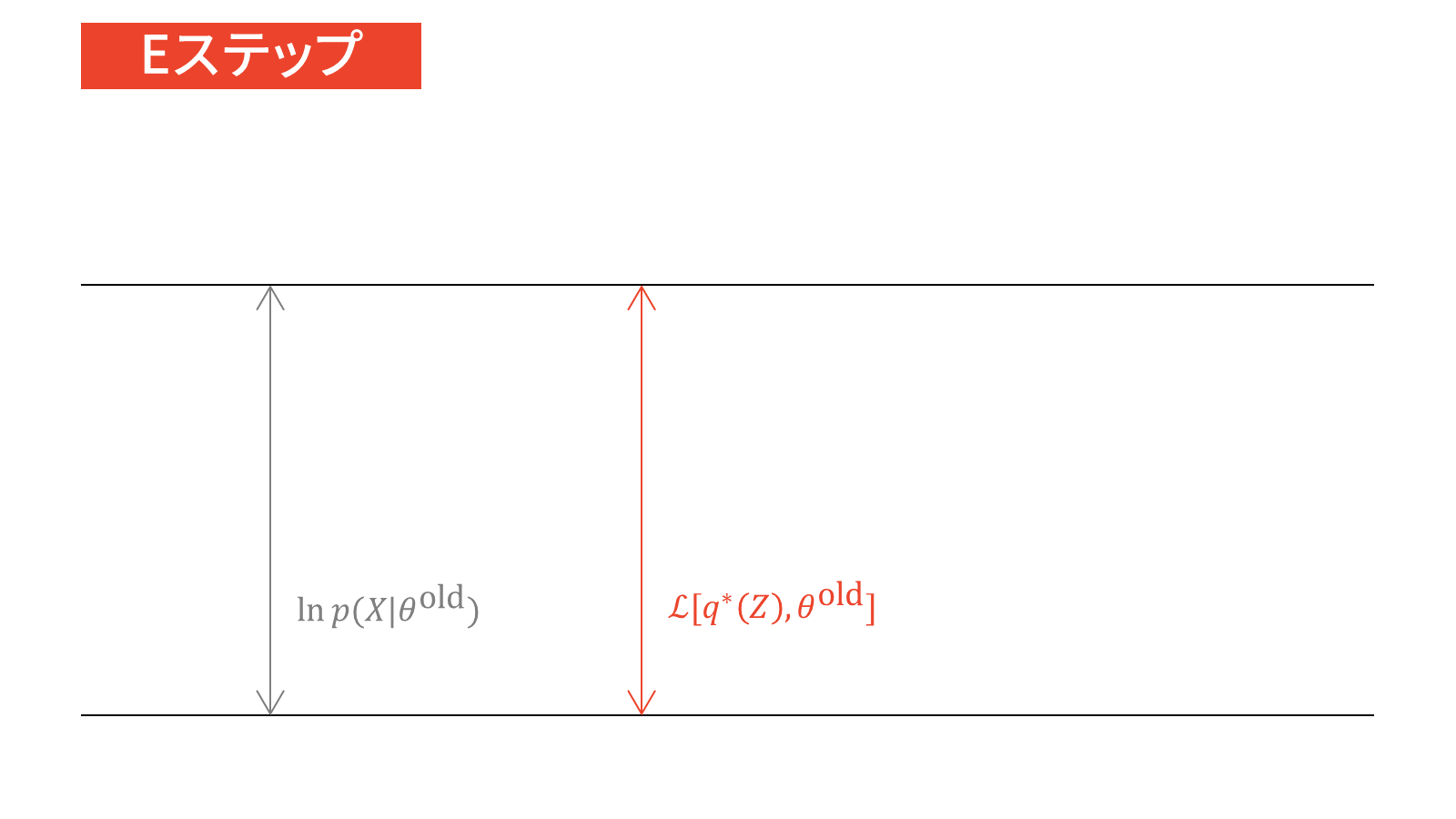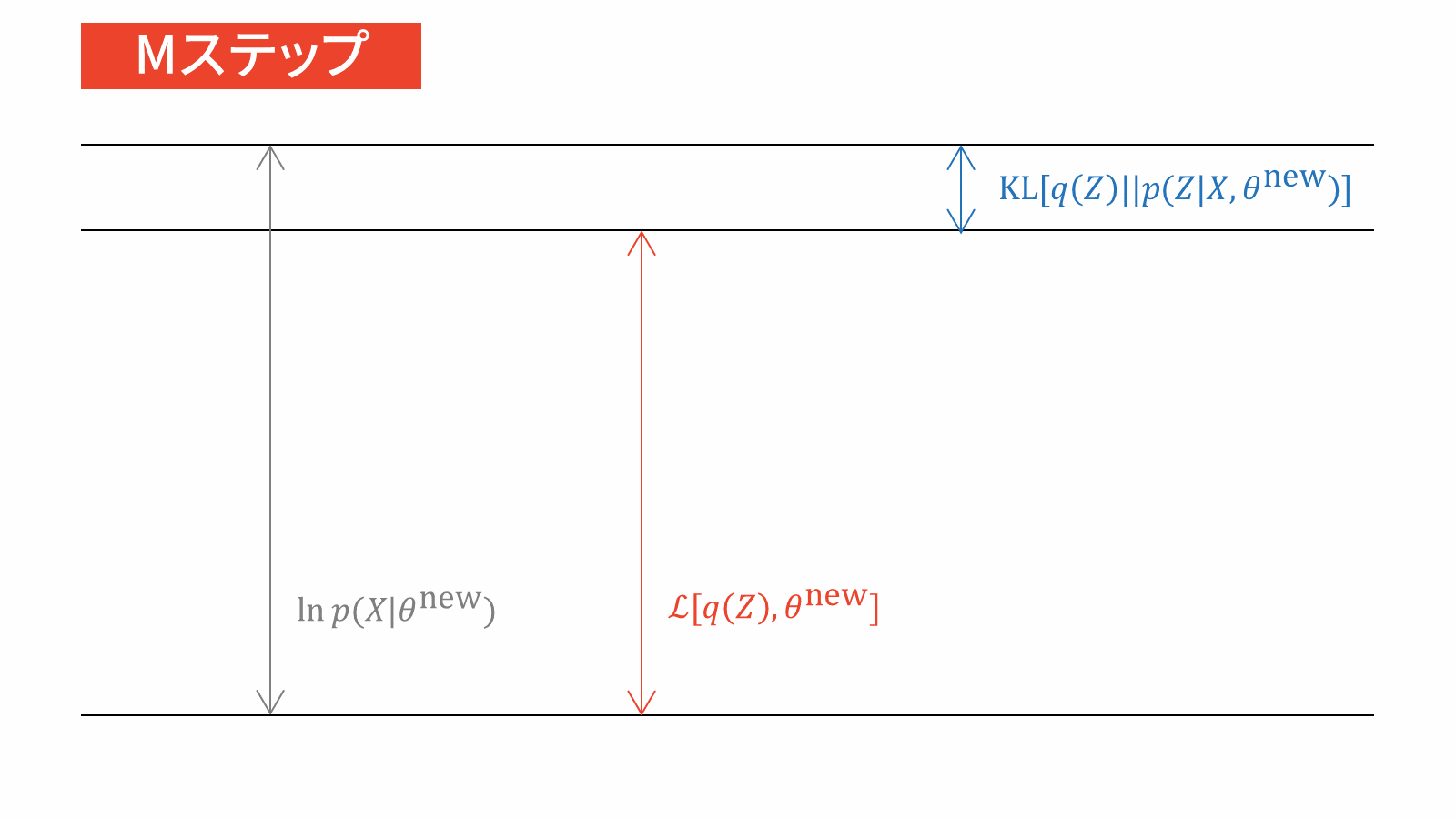
変分ベイズでは,パラメータと潜在変数を同一視しますので,$\theta$は$q(Z)$に吸収されます。つまり,式($\ref{eq_EM}$)の両辺における$\theta$を単に消去して,$q(Z)$の中に$\theta$を含めてあげればよいのです。
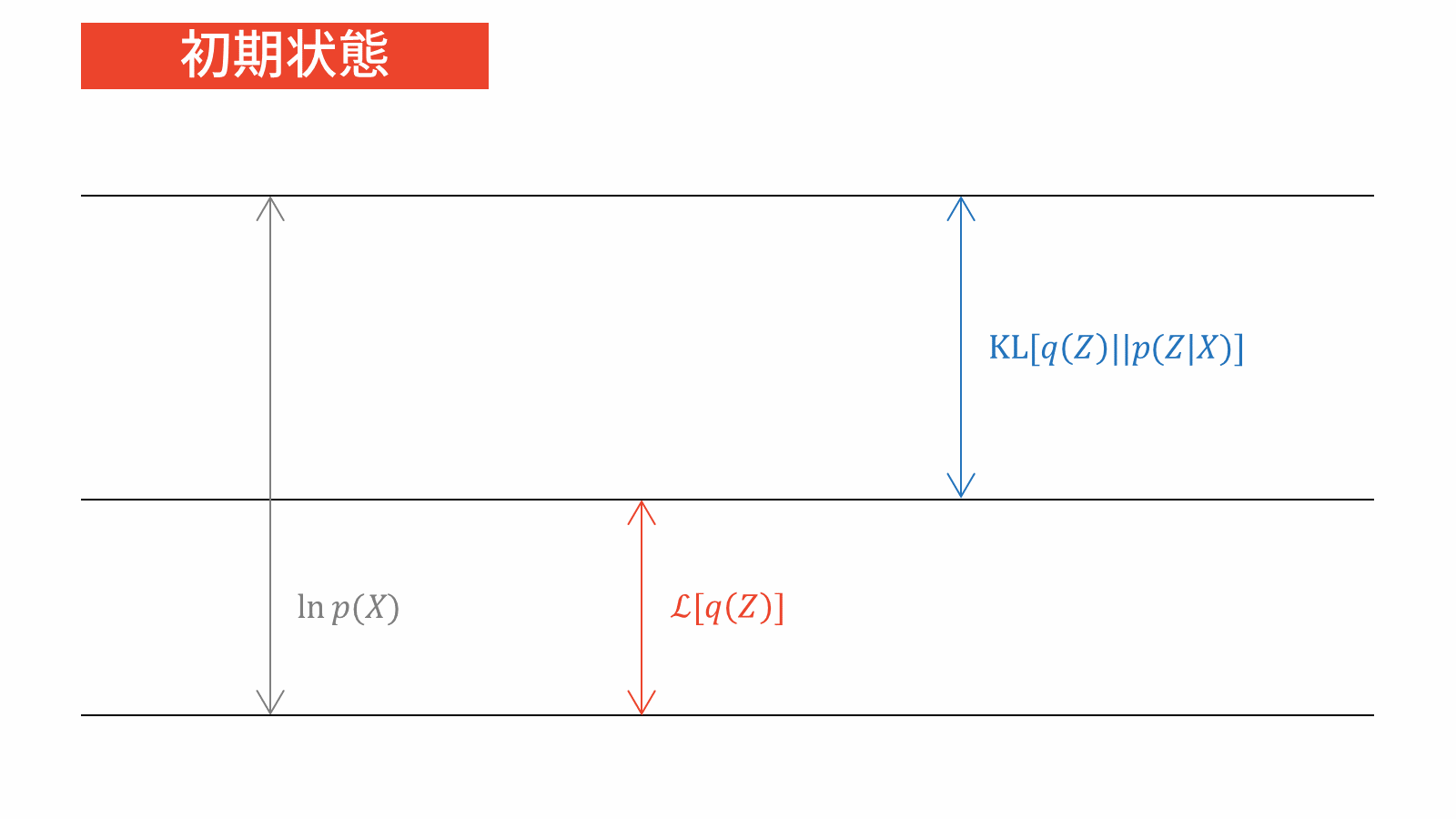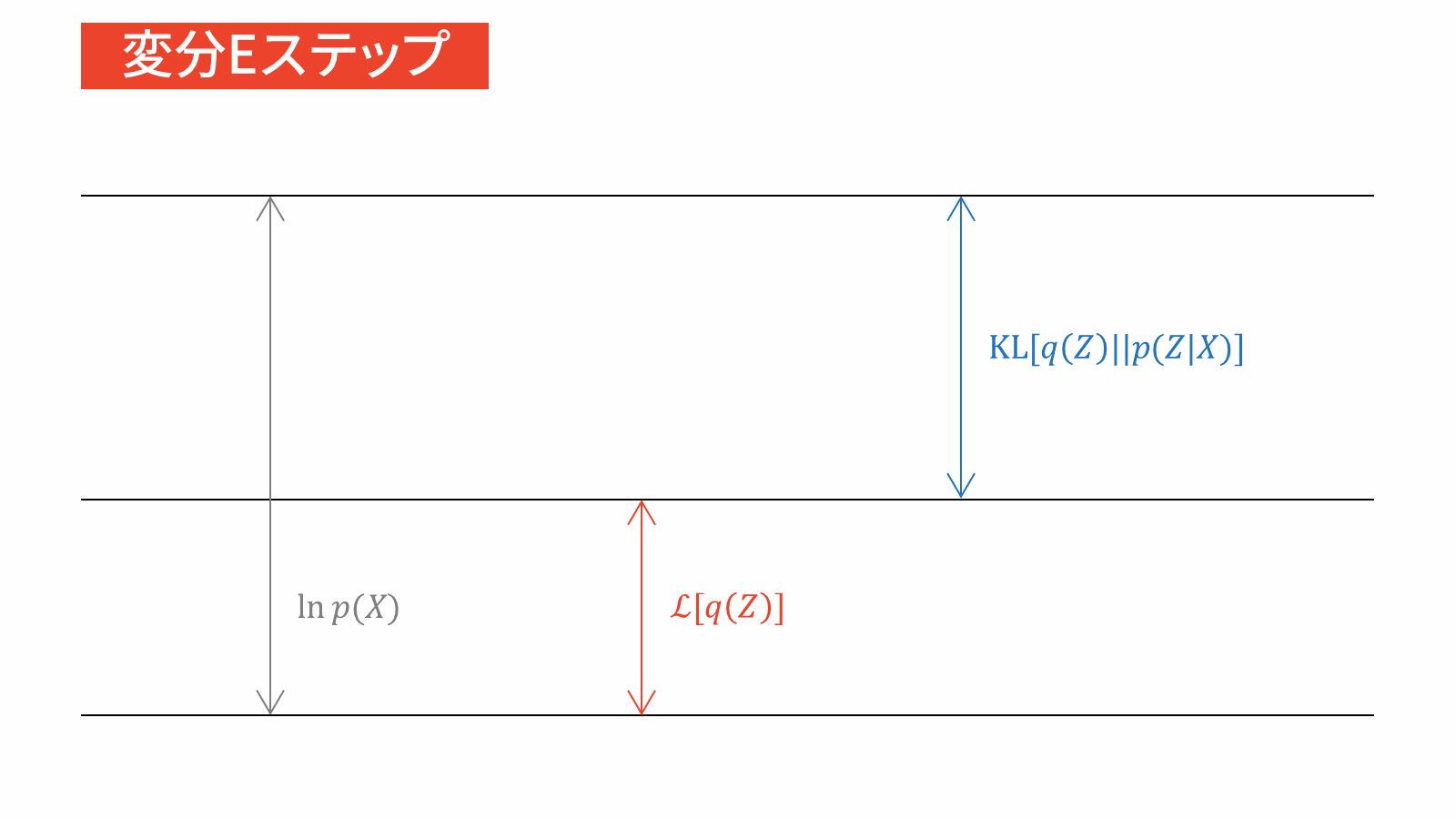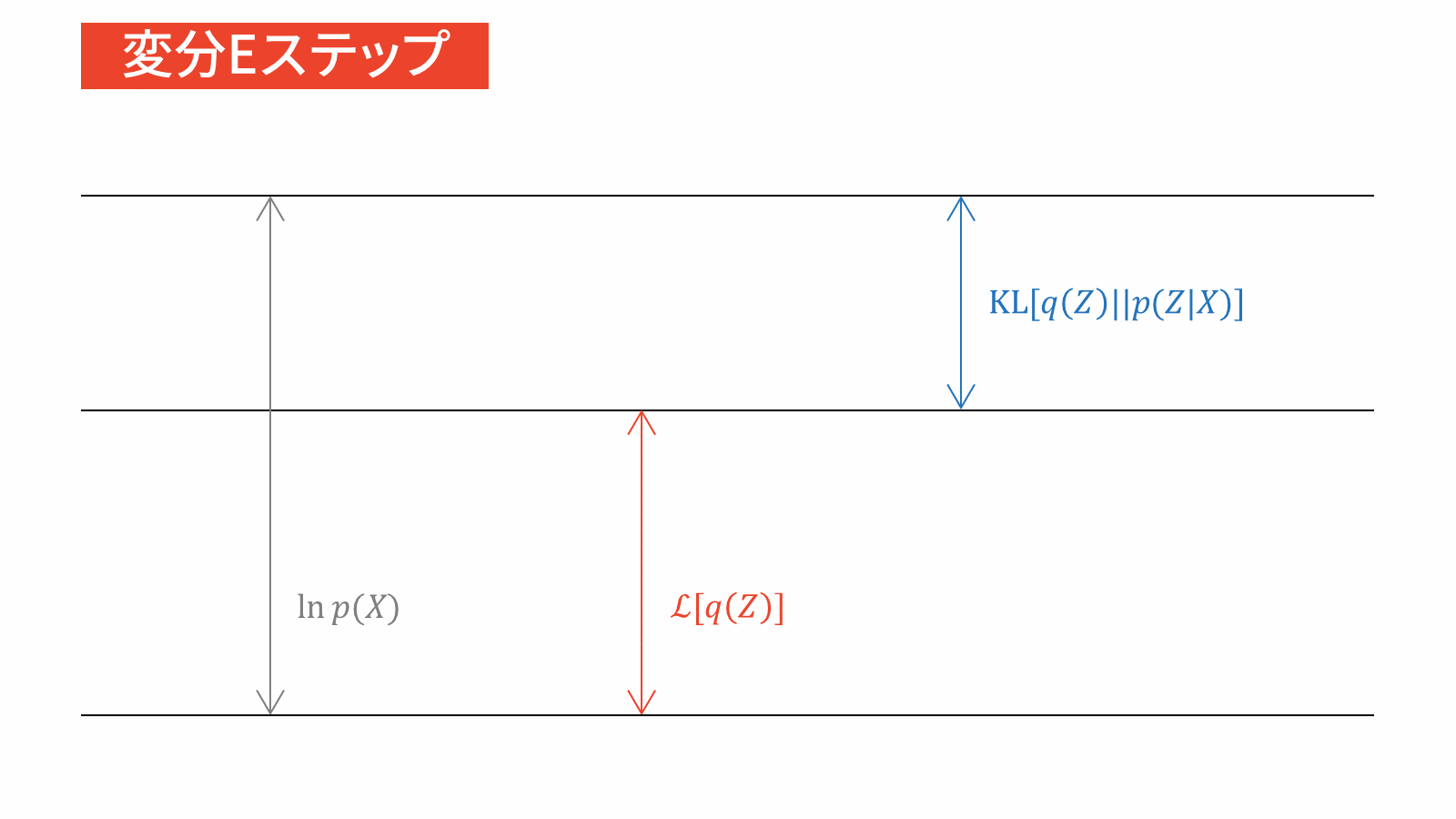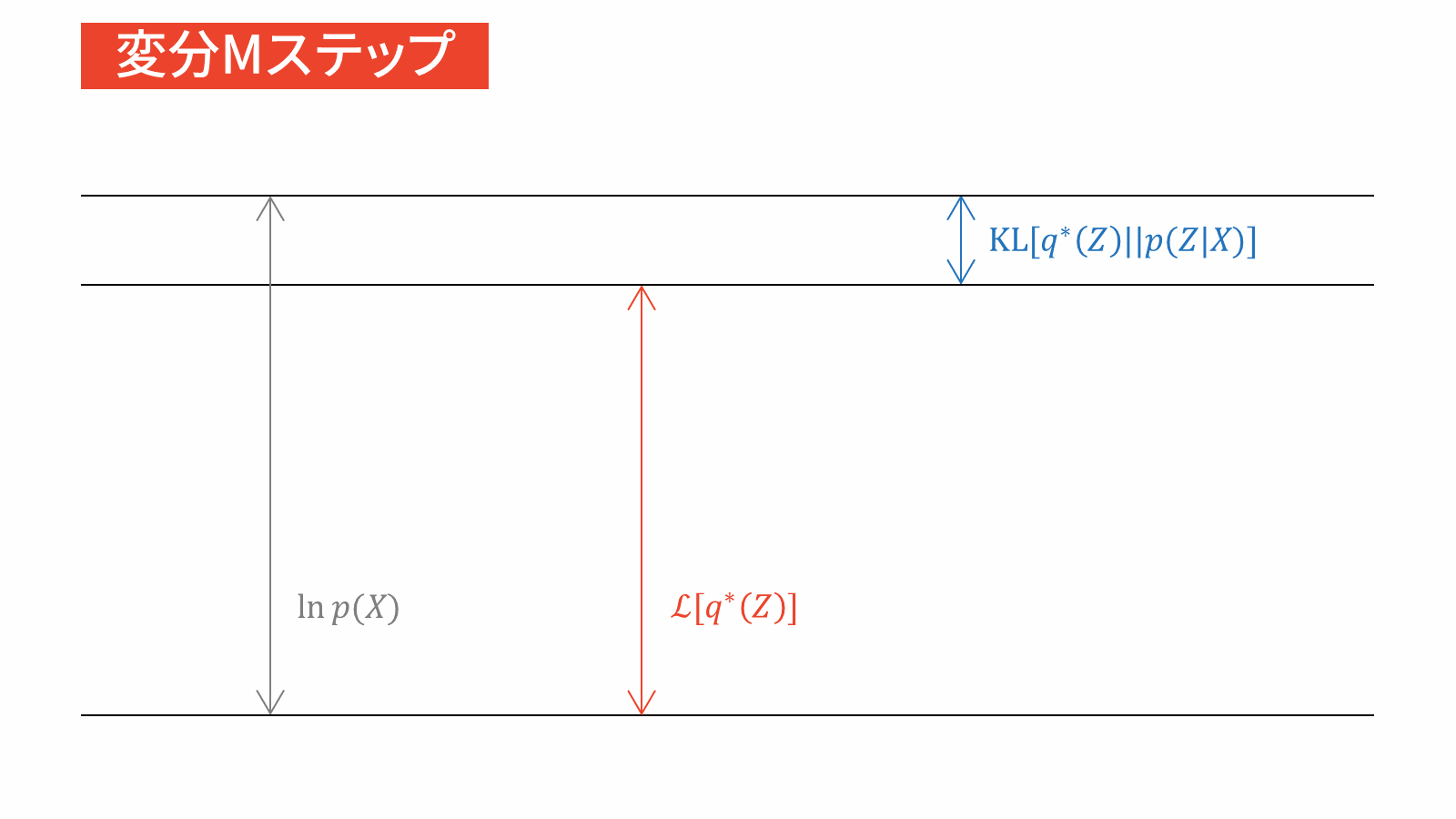
\ln p(X) &= \calL_{\VB} \left[ q(Z) \right] + \KL \left. \left[ q(Z) \right\| p(Z|X) \right] \label{eq_VB}
\end{align}
なぜパラメータを潜在変数に含めるのかについては,変分ベイズではパラメータの値自体には興味がなく,パラメータの分布に興味があるからです。興味の対象は$\theta$ではなく$q$になりますので,$\theta$を$Z$に含めてしまって$q$だけに注目するように仕向けたのです。
すると,変分ベイズの目的関数は式($\ref{eq_VB}$)の左辺,すなわち周辺対数尤度関数であることが分かりました。ここで注意するべきなのは,$X$は観測データですので周辺対数尤度関数は定数であるということです。この事実は変分ベイズ法の解説でよく誤解されている点ですので,おさえておくと良いと思います。
このことから,周辺対数尤度関数を目的関数に掲げるのは不適切といえます。そこで,式($\ref{eq_VB}$)の右辺に注目しましょう。対数周辺尤度関数の下限とKLダイバージェンスから構成されていますね。何を隠そう,第二項目のKLダイバージェンスは前の方針で考えた$q$と$p$の距離を測る指標そのものです。したがって,変分ベイズの目的関数は$q$と$p$のKLダイバージェンスに帰着します。
先ほど「距離指標としてKLダイバージェンスを採用する必然性が(今のところ)ない」とお伝えしましたが,KLダイバージェンスを用いる必然性は,目的関数の下限をイェンセンの不等式で評価していたことに裏付けられているのです。イェンセンの不等式を用いると言う前提に立つ場合には,KLダイバージェンスを用いる必然性は担保されるということです。
ここまでをまとめます。変分ベイズの目的関数は対数周辺尤度関数ですが,一定値であるため目的関数としては不適切です。そこで,対数周辺尤度関数を構成する2つの項に注目すると,$p$をよく近似する$q$を見つけるためにKLダイバージェンスを目的関数に設定すれば良いことが分かりました。
一方で,式($\ref{eq_VB}$)の右辺の和が一定値であることに注意すると,KLダイバージェンスを最小化することは下限を最大化することと等価です。したがって,変分ベイズでは2つの等価な目的関数が存在することになります。ただし,KLダイバージェンスでは最小化問題,下限では最大化問題を考えるという点に注意してください。
最後に,EMアルゴリズムと変分ベイズの比較表を載せておきます。
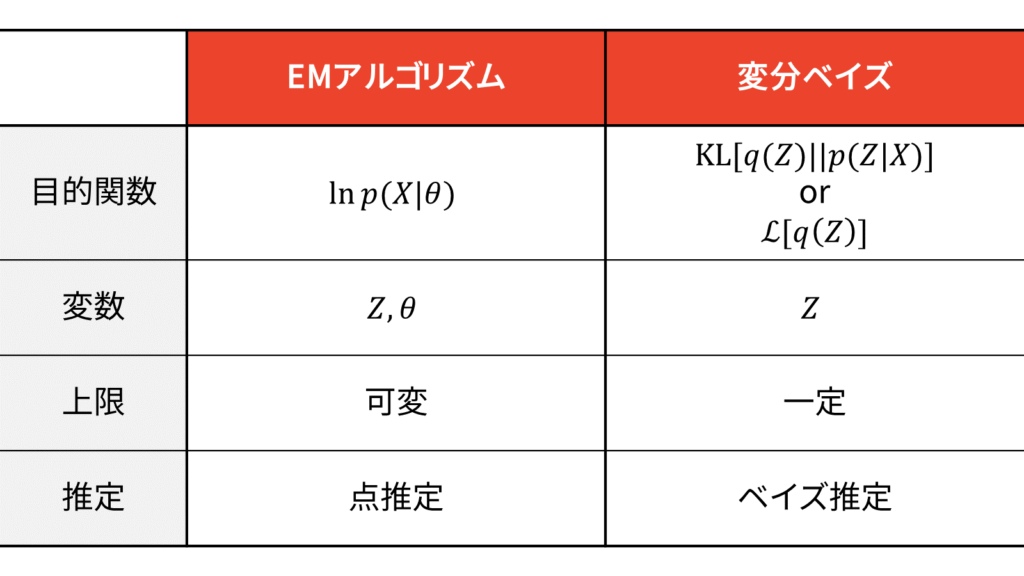
$\calL_{\VB} [q(Z)]$のことをELBO(evidence lower bound)や変分下限(variational lower bound: VLB)と呼びます。先ほどお伝えしたように,lower boundは下界ですから,VLBは正確には変分下界と訳されるべきですが,変分ベイズでは専らイェンセンの不等式により下界を導出することから,下界を下限と呼ぶようになったと推察されます。
最尤推定とMAP推定とのつながり
本章では,変分ベイズの最尤推定とMAP推定とのつながりを説明していきましょう。結論からお伝えすると,最尤推定とMAP推定は,変分ベイズの特殊な場合に相当します。このような文脈で,変分ベイズは点推定の上位互換の概念であるといえるでしょう。KLダイバージェンスを目的関数と捉えた場合でも,下限を目的関数と捉えた場合でも,最尤推定とMAP推定とのつながりを美しく説明することができます。
変分ベイズがどのような場合でも必ず点推定よりも優れているという訳ではありません。上位互換というのはあくまでも概念としての包含関係の話であって,パラメータ推定の性能に関する話ではありません。実際には,与えられたデータ量や利用できるリソースに応じて,点推定とベイズ推定のメリットとデメリットを比較しながら臨機応変に使い分ける必要があります。
KL最小化
ベイズ推論ではパラメータの近似事後分布を求めるのでした。点推定ではパラメータの値を求めるのでした。そこで,ベイズ推論における近似事後分布を「一点にしか値を持たない」関数とすれば,ベイズ推論は点推定と等価になります。数学の世界では「一点にしか値を持たない」関数としてディラックのデルタ関数が有名です。
任意の実連続関数$f : \bbR \rightarrow \bbR$に対し,
\int_{-\infty}^{\infty} f(x) \delta(x) dx &= f(0)
\end{align}
を満たす実数値シュワルツ超関数$\delta$をディラックのデルタ関数と呼ぶ。
例えば,ディラックのデルタ関数を$a$だけ平行移動させると,以下のように$f(a)$が抽出されます。
\int_{-\infty}^{\infty} f(x) \delta(x-a) dx &= f(a)
\end{align}
したがって,パラメータを含む潜在変数の最適解を$\hat{Z}$とおくと,近似事後分布にディラックのデルタ関数$\delta(Z-\hat{Z})$を仮定すればよいことが分かります。
&\KL \left. \left[ \delta \left(Z-\hat{Z} \right) \right\| p(Z|X) \right] \notag \\[0.7em]
&= \int \delta \left(Z-\hat{Z} \right) \ln \frac{\delta(Z-\hat{Z})}{p(Z|X)} dZ \\[0.7em]
&= \int \delta \left(Z-\hat{Z} \right) \ln \delta \left(Z-\hat{Z} \right) dZ-\int \delta \left(Z-\hat{Z} \right) \ln p(Z|X) dZ \\[0.7em]
&= \ln \delta \left(\hat{Z}-\hat{Z} \right)-\ln p(\hat{Z}|X) \\[0.7em]
&= \ln \delta(0)-\ln p(\hat{Z}|X)
\end{align}
結局,最適解$\hat{Z}$は以下のように表されます。$\ln \delta(0)$は定義されませんが,$\hat{Z}$とは関係ないため無視できる点がポイントです。
\argminHatZ \KL \left. \left[ \delta \left(Z-\hat{Z} \right) \right\| p(Z|X) \right]
&= \argminHatZ \left\{ \ln \delta(0)-\ln p(\hat{Z}|X) \right\} \\[0.7em]
&= \argmaxHatZ \ln p(\hat{Z}|X) \\[0.7em]
&= \argmaxHatZ p(\hat{Z}|X) \label{eq_VB_MAP}
\end{align}
これはMAP推定そのものを表していますよね。美しいです。さらに,MAP推定において事前分布が一様(つまりパラメータに関する情報が得られない)と仮定したケースは,最尤推定に相当するはずです。そこで,式($\ref{eq_VB_MAP}$)において事前分布として定数$p(\hat{Z})=C_{\ML}$を仮定してみましょう。
\argminHatZ \KL \left. \left[ \delta \left(Z-\hat{Z} \right) \right\| p(Z|X) \right]
&= \argmaxHatZ \ln p(\hat{Z}|X) \\[0.7em]
&= \argmaxHatZ \ln \frac{p(X|\hat{Z})p(\hat{Z})}{p(X)} \\[0.7em]
&= \argmaxHatZ \left\{ \ln p(X|\hat{Z}) + \ln p(\hat{Z})-\ln p(X) \right\} \\[0.7em]
&= \argmaxHatZ \left\{ \ln p(X|\hat{Z}) + C_{\ML}-\ln p(X) \right\} \\[0.7em]
&= \argmaxHatZ \ln p(X|\hat{Z}) \\[0.7em]
&= \argmaxHatZ p(X|\hat{Z})
\end{align}
これは最尤推定そのものを表していますよね。美しいです。ここまでの流れをまとめておきましょう。
変分ベイズのKL最小化の文脈において,以下の仮定と推定方法が対応する。
- 近似事後分布にディラックのデルタ関数を仮定
- MAP推定に相当
- 近似事後分布にディラックのデルタ関数を仮定かつ事前分布に定数を仮定
- 最尤推定に相当
シュワルツ超関数は単に超関数とも呼ばれていて,関数を拡張した概念です。ディラックのデルタ関数は元々,空間の一点にだけ存在する粒子を表現するために考案された関数です。上の定義の通り,積分して初めて意味をもつことから,一般的な関数とは異なる超関数として定義されています。
下限最大化
下限最大化の文脈においては,KL最小化の文脈よりもシンプルにMAP推定と最尤推定との繋がりを示すことができます。EMアルゴリズムにおける下限$\calL_{\ML}$の定義より,変分ベイズにおける下限$\calL_{\VB}$は以下のように計算されます。ただし,変分ベイズでは潜在変数を連続値として扱うため,シグマを積分で置き換えています。
\calL_{\VB} \left[ q(Z) \right] &= \int_{Z} q(Z) \ln \frac{p(X, Z)}{q(Z)} dZ \\[0.7em]
&= \int_{Z} q(Z) \ln \frac{p(X|Z)p(Z)}{q(Z)} dZ \\[0.7em]
&= \int_{Z} q(Z) \ln p(X|Z) dZ-\int_{Z} q(Z) \ln \frac{q(Z)}{p(Z)} dZ \\[0.7em]
&= \int_{Z} q(Z) \ln p(X|Z) dZ-\KL \left. \left[ q(Z) \right\| p(Z) \right] \label{eq_l_vb}
\end{align}
変分ベイズでは,この下限を最大化していくのでした。したがって,変分ベイズでは式($\ref{eq_l_vb}$)の第一項目の下限は最大化され,第二項目のKLダイバージェンスは最小化されます。同時に二つの項を考えると大変ですので,それぞれを最大化する場合について考えてみましょう。
第一項目の最大化は対数尤度に対応しますので,第一項目だけを考えると最尤推定に相当することが分かります。実際,第一項目を最大にする$q$は,対数尤度を最大にする$\hat{Z}$で値をもつディラックのデルタ関数$\delta(Z-\hat{Z})$になります。なぜなら,期待値は分布の平均に相当する概念を表しますが,期待値を最大にするためには分布の最大値を抽出すれば良いからです。この結果は,KL最小化文脈の考察と一致します。
第二項目は負のKLダイバージェンスに対応しますので,第二項目だけを考えると「事後分布$q(Z)$を事前分布$p(Z)$に近づける」ことに相当することが分かります。これは,MAP推定における事前分布の正則化項に対応しており,KL最小化文脈の考察と一致します。
結局,下限を二つの項に分解すると以下のような結果になることが分かりました。用語に数学的な厳密性は担保していません。
\text{下限} &= q\text{による対数尤度の期待値} + \text{近似分布と事前分布の負の距離} \\[0.7em]
&= \text{最尤推定項} + \text{正則化項}
\end{align}
このように,下限を最大化することは,第1項目を大きくする(最尤推定の効果を大きくする)か,第2項目を大きくする(正則化の効果を大きくする)かのバランスを取っていることが分かりました。以上をまとめます。
変分ベイズの下限最大化の文脈において,下限は以下のように分解される。
\text{下限} &= \text{最尤推定項} + \text{正則化項}
\end{align}
混合ガウス分布への適用
本章では,混合ガウス分布(GMM:Gaussian Mixture Model)を題材に,EMアルゴリズムと変分ベイズを応用する方法をお伝えしていきます。
EMアルゴリズム
結論からお伝えすると,EMアルゴリズムのGMMへの適用は以下のようにまとめられます。
EMアルゴリズムのGMMへの適用(GMM-EM)は,以下の4ステップから構成される。
- 初期値設定
- 負担率$r_{nk}$と$\calQ$関数の計算(Eステップ)
- 各パラメータの更新(Mステップ)
- 収束判定
まずは各パラメータに初期値$\vmu_0$,$\mSigma_0$,$\pi_0$を与える。次に,以下のEステップとMステップを収束するまで繰り返す。
Eステップ
以下の負担率$r_{nk}$と$\calQ$関数を計算する。
r_{nk} &= \frac{\pi_k \N (\vx_n | \vmu_k, \mSigma_k)} {\sum_{j=1}^{K} \pi_j \N (\vx_n | \vmu_j, \mSigma_j)} \\[0.7em]
\calQ(\theta) &= \sum_{n=1}^{N} \sum_{k=1}^{K} r_{nk} \left[-\frac{1}{2}\left\{ \ln |\mSigma_k|-(\vx_n-\vmu_k)^{T}\mSigma_k^{-1}(\vx_n-\vmu_k) \right\} \right]
\end{align}
Mステップ
$\calQ$関数を最大にするように以下のパラメータを計算する。
N_k &= \sum_{n=1}^{N} r_{nk} \\[0.7em]
\vmu_k &= \frac{\sum_{n=1}^{N} r_{nk} \vx_n}{N_k} \\[0.7em]
\mSigma_k &= \frac{\sum_{n=1}^{N} r_{nk} (\vx_n-\vmu_k)(\vx_n-\vmu_k)^T}{N_k} \\[0.7em]
\pi_k &= \frac{N_k}{N}
\end{align}
詳しい導出方法は「EMアルゴリズムをはじめからていねいに」をご参照下さい。
変分ベイズ
本節では,以下の流れで変分ベイズをGMMのパラメータ推論に適用していきます(GMM-VB)。
- 同時分布の依存関係確認
- 平均場近似のグループ分けの仮定
- 更新式適用による変分下限の最大化
1. 同時分布の依存関係確認
本節では,潜在変数とパラメータの依存関係をグラフィカルモデルを通して確認します。GMMのパラメータは,潜在変数も含めると,$\mZ, \vpi, \vmu, \mSigma$です。今回仮定する依存関係は,一般的によく利用されるものです。以下にグラフィカルモデルを示します。
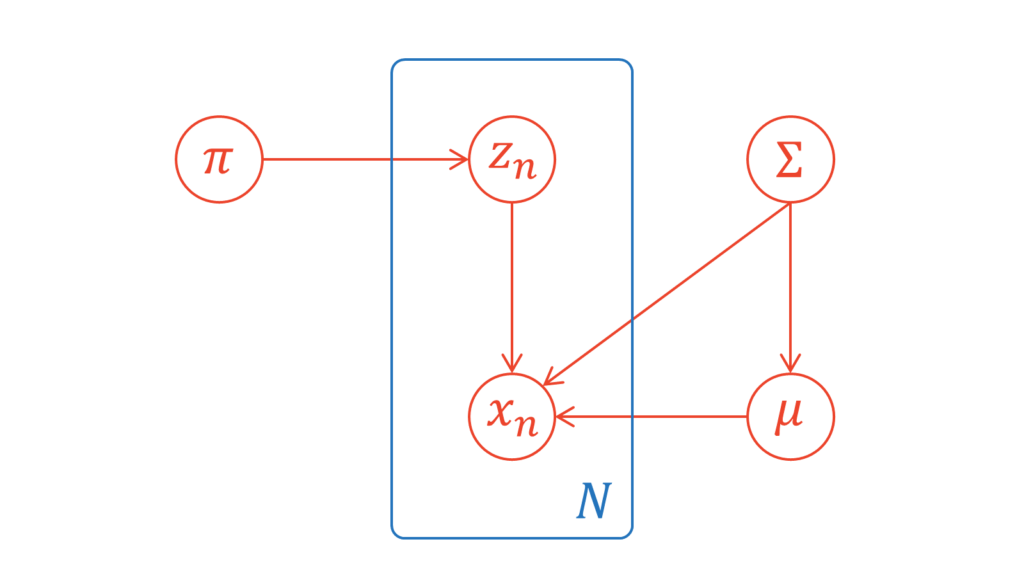
これを数式を用いて表すと,以下のようになります。
p(\mX, \mZ, \vpi, \vmu, \mSigma) &= p(\mX | \mZ, \vmu, \mSigma) p(\mZ | \vpi) p(\vpi) p(\vmu | \mSigma) p(\mSigma)
\end{align}
今回は,各分布を以下のように定めます。
p(\mX | \mZ, \vmu, \mSigma) &= \prod_{n=1}^{N} \prod_{k=1}^{K} \N (\vx_n | \vmu_k, \mSigma_k^{-1})^{z_{nk}} \\[0.7em]
p(\mZ | \vpi) &= \prod_{n=1}^{N} \prod_{k=1}^{K} \pi_k^{z_{nk}} \\[0.7em]
p(\vpi) &= \Dir (\vpi | \valpha_0) \label{p_pi} \\[0.7em]
p(\vmu | \mSigma) &= \prod_{k=1}^{K} \N \left\{ \vmu_k | \vm_0, (\beta_0 \mSigma_k)^{-1} \right\} \label{p_mu_sigma} \\[0.7em]
p(\mSigma) &= \prod_{k=1}^{K} \W (\mSigma_k | \mW_0, \nu_0) \label{p_sigma}
\end{align}
EMアルゴリズムとの対応を図るために,$\mZ$の周辺尤度関数も確認しておきます。
p(\mX | \vmu, \mSigma, \vpi) &= \sum_{\mZ} p(\mX, \mZ | \vmu, \mSigma, \vpi) \\[0.7em]
&= \sum_{\mZ} p(\mX | \mZ, \vmu, \mSigma) \cdot p(\mZ | \vpi) \\[0.7em]
&= \sum_{\mZ} \left[ \prod_{n=1}^{N} \prod_{k=1}^{K} \left\{ \pi_{k} \N (\vx_n | \vmu_k, \mSigma_k^{-1})\right\}^{z_{nk}} \right] \\[0.7em]
&= \prod_{n=1}^{N} \sum_{k=1}^{K} \pi_{k} \N (\vx_n | \vmu_k, \mSigma_k^{-1})
\end{align}
ただし,最終行は「one-hot-vector$\mZ$の全ての候補について足し合わせる」操作を「全てのクラス$k$について和をとる」操作に読み替えて変形しました。この結果は,GMM-EMにおける以下の周辺尤度関数と矛盾しません。
p(\vx_n|\vpi, \vmu, \mSigma) &= \sum_{k=1}^K \pi_k \N (\vx_n | \vmu_k, \mSigma_k)
\end{align}
繰り返しにはなりますが,変分ベイズはEMアルゴリズムとは異なりベイズ推定を行いますので,尤度関数に加えて$\vpi$,$\vmu$,$\mSigma$の事前分布を設定します。
分散共分散行列に関するガウス分布の共役事前分布は逆ウィシャート分布になります。一方で,分散共分散行列の逆行列に関するガウス分布の共役事前分布はウィシャート分布になります。今回は,素朴なウィシャート分布を持ち出すために,ガウス分布の分散共分散行列を逆行列で定めます。なお,分散共分散行列の逆行列のことを精度行列(precision matrix)と呼びます。
以下では,簡単に尤度関数と事前分布の根拠を説明しておきます。
EMアルゴリズムと同様に,$\mZ$の条件付き分布は$\vz_n$と$\vpi$の性質から自然に導かれる関係です。$\vz_n$はone-hot-vectorですので,$\vz_n$の生成確率を$\pi_k$を利用して表現すれば,上のように累乗と総乗で表すことができるのです。データの条件付き確率も同様に,$\vz_n$がone-hot-vectorであることを利用して表現できます。
$\vpi$の事前分布がディリクレ分布であるのは,$p(\mZ | \vpi)$が多項分布の形($n=1$のカテゴリカル分布)をしており,その共役事前分布として定めているからです。同様に,多変量正規分布$p(\mX | \mZ, \vmu, \mSigma)$の$\vmu$に関する共役事前分布としてガウス分布,精度行列(分散共分散行列の逆数)に関する共役事前分布としてウィシャート分布を設定しています。
多くの書籍やWeb上の資料では「$p(\vmu, \mSigma)$の共役事前分布としてガウスウィシャート分布を仮定する」と説明されています。しかし,本稿では上で示したグラフィカルモデルに基づいた説明を心掛けています。すなわち,まず$\mSigma$が生成されて,その$\mSigma$に依存して$\vmu$が生成されるというフローを忠実に再現するために,$\vmu$に関する共役事前分布と$\mSigma$に関する共役事前分布を別々に説明しました。
以下では,これらの分布を使って計算を行うために定義を確認しておきましょう。具体的には,ディリクレ分布,多変量正規分布,ウィシャート分布の確率密度関数と期待値を知っておく必要があります。ディリクレ分布とウィシャート分布に関しては,後で$E[\ln x]$を利用することになるため,ここで一緒に確認しておきましょう。
ディリクレ分布の確率密度関数・$E[X]$・$E[\ln x]$は以下のように表されます。
f_{\mX}(\vx) &= \frac{1}{B(\valpha)} \prod_{i=1}^{n} x_{i}^{\alpha_{i}-1} \\[0.7em]
E[X_i] &= \frac{\alpha_i}{\sum_{i=1}^n \alpha_i} \label{e_pi} \\[0.7em]
E[\ln X_i] &= \psi(\alpha_i)-\psi\left( \sum_{i=1}^n \alpha_i \right)
\end{align}
ただし,$B(\cdot)$はベータ関数,$\psi(\cdot)$はディガンマ関数を表す。
B(a, b) &= \int_0^1 x^{a-1}(1-x)^{b-1}dx \\[0.7em]
\psi(a) &= \frac{d}{da} \ln \Gamma(a)
\end{align}
多変量正規分布の確率密度関数・$E[X]$は以下のように表されます。
f_{\mX}(\vx) &= \frac{1}{(2\pi)^{d/2}|\Sigma|^{1/2}}\exp \left\{ -\frac{1}{2}(\vx-\vmu)^T \Sigma^{-1}(\vx-\vmu) \right\} \\[0.7em]
E[\mX] &= \vmu \label{e_mu}
\end{align}
ウィシャート分布の確率密度関数・$E[X]$・$E[\ln x]$は以下のように表されます。
\W (\mSigma | \mW, \nu) &= C(\mW, \nu)|\Sigma|^{(\nu-D-1)/2} \exp\left(-\frac{1}{2} \Tr \left[\mW^{-1}\mSigma \right] \right) \\[0.7em]
E[\mSigma] &= \nu \mW \label{e_sigma}\\[0.7em]
E[\ln |\mSigma|] &= \sum_{i=1}^{D} \psi\left( \frac{\nu + 1-i}{2} \right) + D \ln 2 + \ln |\boldsymbol{W}|
\end{align}
ただし,$C(\cdot, \cdot)$は以下で表される定数,$\psi(\cdot)$はディガンマ関数である。
C(\mW, \nu) &= |\mW|^{-\nu/2} \left\{ 2^{\nu D/2} \pi^{{D(D-1)}/4} \prod_{i=1}^{D}\Gamma\left( \frac{\nu + 1-i}{2} \right) \right\}^{-1} \\[0.7em]
\psi(a) &= \frac{d}{da} \ln \Gamma(a)
\end{align}
特に,$\mW$が対称行列であることに注意されたい。
分布を利用する準備が整いました。これにて「1. 同時分布の依存関係の確認」が完了しました。
2. 平均場近似のグループ分けの仮定
本節では,平均場近似のグループ分けを考えていきます。今回は,潜在変数と他のパラメータが独立であることを仮定しましょう。
q(\mZ, \vpi, \vmu, \mSigma) &= q(\mZ)q(\vpi, \vmu, \mSigma)
\end{align}
この仮定は$\mZ$と$\{\vpi, \vmu, \mSigma\}$が独立であることを仮定しているだけであり,$\mZ$と$\vpi$が独立であることは仮定していません。$\mZ$と$\vpi$が独立であるための必要十分条件は,$\mZ,\vpi$の同時分布がそれぞれの確率分布の積で分離されることであり,$\mZ,\vpi$以外も含まれる同時分布から$\mZ$のみが分離されたからといって$\mZ$と$\vpi$が独立になるとは限りません。
「1. 同時分布の依存関係確認」で仮定したように,$\vpi$と$(\vmu, \mSigma)$は独立ですから,$q(\vpi, \vmu, \mSigma)$を$q(\vpi)$と$q(\vmu, \mSigma)$に分解してもよいです。しかし,次節で計算して分かる通り,分解せずとも$\vpi$と$\vmu, \mSigma$が独立である結果が導かれますから,ここではより弱い仮定を採用することにします。これにて「2. 平均場近似のグループ分けの仮定」が完了しました。
3. 更新式適用による変分下限の最大化
本節では,変分ベイズの更新式を用いて変分下限を最大化します。「2. 平均場近似のグループ分けの仮定」では,潜在変数$\mZ$の属する分布とパラメータ$\vpi, \vmu, \mSigma$の属する分布が別々であると仮定しました。そこで,以下では潜在変数に関する最適化を考えた後に,パラメータに関する最適化を考えます。EMアルゴリズムの類推により,前者の最適化をEステップ,後者の最適化をMステップとみなせます。
管理人の考えでは,変分ベイズではEステップとMステップを分ける意味はあまりないと考えています。なぜなら,変分ベイズではEMアルゴリズムとは異なり,パラメータと潜在変数を同一視するからです。一方で,本稿の趣旨はEMアルゴリズムとの比較を通じて変分ベイズをはじめからていねいに理解することです。そのため,今回は変分ベイズにおけるEステップを変分Eステップ,Mステップを変分Mステップと表記することにします。詳しくは末尾の付録で説明します。
最初に結論からお伝えします。
変分ベイズのGMMへの適用(GMM-VB)は,以下の4ステップから構成される。
- 初期値設定
- 負担率$r_{nk}$の計算(変分Eステップ)
- 各パラメータの更新(変分Mステップ)
- 収束判定
まずは各パラメータに初期値$\alpha_0$,$\beta_0$,$\nu_0$,$\vm_0$,$\mW_0$を与える。次に,以下の変分Eステップと変分Mステップを収束するまで繰り返す。
変分Eステップ
負担率$r_{nk}$を計算する。
r_{nk} &= \frac{\rho_{nk}}{\sum_{j=1}^{K} \rho_{nj}}
\end{align}
ただし,$\rho_{nk}$は以下で計算できる。
\ln \tilde{\pi}_k &= \psi (\alpha_k)-\psi \left( \sum_{k=1}^{K} \alpha_k \right) \\[0.7em]
\ln \tilde{\Sigma}_k &= \sum_{i=1}^{D} \psi\left( \frac{\nu_k + 1-i}{2} \right) + D \ln (2) + \ln |\mW_k| \\[0.7em]
\rho_{nk} &= \tilde{\pi}_k \tilde{\mSigma}_k ^{\frac{1}{2}} \exp \left\{-\frac{D}{2 \beta_k}-\frac{\nu_k}{2}(\vx_n-\vm_k)^T \mW_k(\vx_n-\vm_k) \right\}
\end{align}
変分Mステップ
パラメータを更新する。
\alpha_k &= \alpha_0 + N_k \\[0.7em]
\beta_k &= \beta_0 + N_k \\[0.7em]
\nu_k &= \nu_0 + N_k \\[0.7em]
\vm_k &= \frac{1}{\beta_k} (\beta_0 \vm_0 + N_k \overline{\vx}_k) \\[0.7em]
\mW_k^{-1} &= \mW_0^{-1} + N_k \mS_k + \frac{\beta_0 N_k}{\beta_0 + N_k} (\overline{\vx}_k-\vm_0)(\overline{\vx}_k-\vm_0)^T
\end{align}
ただし,$N_k$,$\overline{\vx}_k$,$\mS_k$は変分Eステップで計算した負担率$r_{nk}$を用いて計算できる。
N_k &= \sum_{n=1}^{N} r_{nk} \\[0.7em]
\overline{\vx}_k &= \frac{1}{N_k} \sum_{n=1}^{N} r_{nk} \vx_n \\[0.7em]
\mS_k &= \frac{1}{N_k} \sum_{n=1}^{N} r_{nk} (\vx_n-\overline{\vx}_k) (\vx_n-\overline{\vx}_k)^T \\[0.7em]
\end{align}
変分Eステップ
まずは変分Eステップの導出から始めましょう。最適な$q$である$q^{\ast} (\mZ)$を求めます。変分ベイズの更新式を適用すると,以下のように$q^{\ast} (\mZ)$を計算することができます。
\ln q^{\ast} (\mZ) &= E_{\vpi, \vmu, \mSigma} \left[ \ln p(\mX, \mZ, \vpi, \vmu, \mSigma) \right] + \const \\[0.7em]
&= E_{\vpi} \left[ \ln p(\mZ | \vpi )] + E_{\vmu, \mSigma}[\ln p(\mX | \mZ, \vmu, \mSigma) \right] + \const \\[0.7em]
&= \sum_{n=1}^{N} \sum_{k=1}^{K} z_{nk} E[\ln \pi_k] + \frac{1}{2} E[\ln |\mSigma_k|]-\frac{D}{2} \ln (2\pi) \notag \\[0.7em]
&\quad\quad-\frac{1}{2}E_{\vmu_k, \mSigma_k} \left[ (\vx_n-\vmu_k)^T \mSigma_k (\vx_n-\vmu_k) \right] + \const \\[0.7em]
&= \sum_{n=1}^{N} \sum_{k=1}^{K} z_{nk} \ln \rho_{nk} + \const
\end{align}
ただし,$\ln \rho_{nk}$は以下のように置きました。
\ln \rho_{nk} &= E[\ln \pi_k] + \frac{1}{2} E[\ln |\mSigma_k|]-\frac{D}{2} \ln (2\pi) \notag \\[0.7em]
&\quad\quad-\frac{1}{2}E_{\vmu_k, \mSigma_k} \left[ (\vx_n - \vmu_k)^T \mSigma_k (\vx_n - \vmu_k) \right] \label{eq_rho}
\end{align}
一旦,定数項$\const$を無視すると,$q^{\ast}(\boldsymbol{Z})$は以下のように求められます。
q^{\ast}(\mZ) &\propto \prod_{n=1}^{N} \prod_{k=1}^{K} \rho_{nk}^{z_{nk}}
\end{align}
以下では,厳密に$q^{\ast}(\boldsymbol{Z})$を定めていきます。すなわち,先ほど無視した定数項$\const$による正規化定数を求めます。求める正規化定数を$A$とおくと,
\frac{1}{A} &= \sum_{\mZ} \prod_{n=1}^{N} \prod_{k=1}^{K} \rho_{nk}^{z_{nk}} \\[0.7em]
&= \left( \sum_{\vz_1} \prod_{k=1}^{K} \rho_{1k}^{z_{1k}}\right) \cdot \left( \sum_{\vz_2} \prod_{k=1}^{K} \rho_{2k}^{z_{2k}} \right) \cdots \\[0.7em]
&= \left( \sum_{k=1}^{K} \rho_{1k} \right) \cdot \left( \sum_{k=1}^{K} \rho_{2k} \right) \cdots \\[0.7em]
&= \prod_{n=1}^{N} \sum_{k=1}^{K}\rho_{nk}
\end{align}
と計算することができます。ただし,途中で$\vz$がone-hot-vectorであることを利用しました。したがって,$q^{\ast}(\mZ)$は正確に以下のように表されます。
q^{\ast}(\mZ)
&= \frac{1}{A}\prod_{n=1}^{N} \prod_{k=1}^{K} \rho_{nk}^{z_{nk}} \\[0.7em]
&= \frac{\prod_{n=1}^{N} \prod_{k=1}^{K} \rho_{nk}^{z_{nk}}}{\prod_{n=1}^{N} \sum_{k=1}^{K}\rho_{nk}} \\[0.7em]
&= \prod_{n=1}^{N} \frac{\prod_{k=1}^{K} \rho_{nk}^{z_{nk}}}{\sum_{k=1}^{K}\rho_{nk}} \\[0.7em]
&= \prod_{k=1}^{N} \frac{\prod_{k=1}^{K} \rho_{nk}^{z_{nk}}}{\prod_{k=1}^{K} \left\{ \sum_{j=1}^{K}\rho_{nj} \right\}^{z_{nk}} } \\[0.7em]
&= \prod_{n=1}^{N} \prod_{k=1}^{K} \left\{ \frac{\rho_{nk}}{\sum_{j=1}^{K} \rho_{nj}} \right\}^{z_{nk} } \\[0.7em]
&= \prod_{n=1}^{N} \prod_{k=1}^{K} r_{nk}^{z_{nk}} \label{eq_q_ast}
\end{align}
ただし,$r_{nk}$は以下のように置きました。
r_{nk} &= \frac{\rho_{nk}}{\sum_{j=1}^{K} \rho_{nj}}
\end{align}
この$r_{nk}$がEMアルゴリズムにおける負担率となります。その証明としては,式($\ref{eq_q_ast}$)の期待値が$r_{nk}$となることから確認できます。$z_{nk}$が$1$のときだけ$r_{nk}$が寄与するからです。
E[z_{nk}] &= r_{nk}
\end{align}
この式は,EMアルゴリズムで定義した負担率と全く同じです。
最後に,式($\ref{eq_rho}$)と事前分布の仮定を利用して,$r_{nk}$を計算するために$\rho_{nk}$を求めましょう。その前に,$D$次元ベクトル$\vx$,$\vmu{\sim}\N(\vm,(\beta\Sigma)^{-1})$,および$\Sigma{\sim}\W(\Sigma|\mW,\nu)$に対し,
E_{\vmu, \Sigma}\left[(\vx-\vmu)^{T}\Sigma(\vx-\vmu)\right] &= \nu(\vx-\vm)^{T}\mW(\vx-\vm)+\beta^{-1}D\label{x^TAxの展開}
\end{align}
が成り立つことを証明します。$\N(\vm, \Sigma)$の確率密度関数を$f_{\N}(\vm,\Sigma)$とおいて$E_{\vmu,\Sigma}$の定義から計算すると,
E_{\vmu,\Sigma}\left[(\vx-\vmu)^{T}\Sigma(\vx-\vmu)\right]
&= \int_{-\infty}^{\infty}\int_{-\infty}^{\infty}(\vx-\vmu)^{T}\Sigma(\vx-\vmu)f_{\N}(\vm,\Sigma)d\vmu d\Sigma\\[0.7em]
&= \int_{-\infty}^{\infty}\left\{\int_{-\infty}^{\infty}(\vx-\vmu)^{T}\Sigma(\vx-\vmu)f_{\N}(\vm|\Sigma)d\vmu\right\}f_{N}(\Sigma)d\Sigma\\[0.7em]
&= \int_{-\infty}^{\infty} E_{\vmu}[(\vx-\vmu)^{T}\Sigma(\vx-\vmu)] f_{N}(\Sigma)d\Sigma\\[0.7em]
&= \int_{-\infty}^{\infty} E_{\vmu}[\Tr\left\{\Sigma(\vx-\vmu)(\vx-\vmu)^{T}\right\}] f_{N}(\Sigma)d\Sigma\\[0.7em]
&= \int_{-\infty}^{\infty} E_{\vmu}[\Tr\left(\Sigma(\vx\vx^{T}-2\vmu\vx^{T}+\vmu\vmu^{T})\right)] f_{N}(\Sigma)d\Sigma\\[0.7em]
&= \int_{-\infty}^{\infty} \Tr\left[E_{\vmu}[\left(\Sigma(\vx\vx^{T}-2\vmu\vx^{T}+\vmu\vmu^{T})\right)]\right] f_{N}(\Sigma)d\Sigma\\[0.7em]
&= \int_{-\infty}^{\infty} \Tr\left[\Sigma(\vx\vx^{T}-2E_{\vmu}[\vmu]\vx^{T}+E_{\vmu}[\vmu\vmu^{T}])\right] f_{N}(\Sigma)d\Sigma\\[0.7em]
&= \int_{-\infty}^{\infty} \Tr\left[\Sigma(\vx\vx^{T}-2\vm\vx^{T}+\vm\vm^{T}+(\beta\Sigma)^{-1})\right] f_{N}(\Sigma)d\Sigma\\[0.7em]
&= \int_{-\infty}^{\infty} \Tr\left[\Sigma(\vx-\vm)(\vx-\vm)^{T}+\Sigma(\beta\Sigma)^{-1}\right] f_{N}(\Sigma)d\Sigma\\[0.7em]
&= \int_{-\infty}^{\infty} \Tr\left[\Sigma(\vx-\vm)(\vx-\vm)^{T}+\beta^{-1} I_{D}\right] f_{N}(\Sigma)d\Sigma\\[0.7em]
&= \int_{-\infty}^{\infty} \left\{\Tr\left[\Sigma(\vx-\vm)(\vx-\vm)^{T}\right]+\Tr\left[\beta^{-1} I_{D}\right]\right\}f_{N}(\Sigma)d\Sigma\\[0.7em]
&= \int_{-\infty}^{\infty} \left\{(\vx-\vm)^{T}\Sigma(\vx-\vm)+\beta^{-1}D\right\} f_{N}(\Sigma)d\Sigma\\[0.7em]
&= E_{\Sigma}\left[\Tr\left[\Sigma(\vx-\vm)(\vx-\vm)^{T}\right]+\beta^{-1}D\right]\\[0.7em]
&= E_{\Sigma}\left[\Tr\left[\Sigma(\vx-\vm)(\vx-\vm)^{T}\right]\right]+\beta^{-1}D\\[0.7em]
&= \Tr\left[E_{\Sigma}\left[\Sigma(\vx-\vm)(\vx-\vm)^{T}\right]\right]+\beta^{-1}D\\[0.7em]
&= \Tr\left[E_{\Sigma}\left[\Sigma\right](\vx-\vm)(\vx-\vm)^{T}\right]+\beta^{-1}D\\[0.7em]
&= \Tr\left[\nu\mW(\vx-\vm)(\vx-\vm)^{T}\right]+\beta^{-1}D\\[0.7em]
&= (\vx-\vm)^{T}\nu\mW(\vx-\vm)+\beta^{-1}D\\[0.7em]
&= \nu(\vx-\vm)^{T}\mW(\vx-\vm)+\beta^{-1}D
\end{align}
となり,式($\ref{x^TAxの展開}$)が示されました。ただし,$X^{T}AX=\Tr[AXX^{T}]$であること,分散共分散行列の定義より
(\beta\Sigma)^{-1}
&= E[(\vmu-\vm)(\vmu-\vm)^{T}]\\[0.7em]
&= E[\vmu\vmu^{T}]-2\vm E[\vmu^{T}]+\vm\vm^{T}\\[0.7em]
&= E[\vmu\vmu^{T}]-2\vm\vm^{T}+\vm\vm^{T}\\[0.7em]
&= E[\vmu\vmu^{T}]-\vm\vm^{T}
\end{align}
となり$E[\vmu\vmu^{T}]{=}\vm\vm^{T}{+}(\beta\Sigma)^{-1}$であること,トレースには線形性があること,ウィシャート分布の期待値が式($\ref{e_sigma}$)で表されること,および期待値とトレースは交換可能であることを利用しました。
$D$次元正方行列$A$を考える。
A &=
\begin{pmatrix}
a_{11} & \cdots & \\
\vdots & \ddots & \\
& & a_{DD}
\end{pmatrix}
\end{align}
期待値の線形性とトレースの定義により,期待値とトレースが交換可能であることが分かる。
E\left[ \Tr\left[ A \right] \right] &= E\left[ \sum_{d=1}^{D}a_{dd} \right] \\[0.7em]
&= \sum_{d=1}^{D} E\left[ a_{dd} \right] \\[0.7em]
&= \Tr\left[
\begin{pmatrix}
E[a_{11}] & \cdots & \\
\vdots & \ddots & \\
& & E[a_{DD}]
\end{pmatrix}
\right] \\[0.7em]
&= \Tr\left[ E\left[ A \right] \right]
\end{align}
式($\ref{x^TAxの展開}$)を今回の仮定$\vmu{\sim}\N\{\vmu_k | \vm_k, (\beta_k \mSigma_k)^{-1}\} $および$\Sigma_{k}{\sim}\W (\mSigma_k | \mW_k, \nu_k) $に適用すると,
E_{\vmu_{k}, \Sigma_{k}}\left[(\vx_{n}-\vmu_{k})^{T}\Sigma_{k}(\vx_{n}-\vmu_{k})\right]
&= \nu_{k}(\vx_{n}-\vm_{k})^{T}W_{k}(\vx_{n}-\vm_{k}) + \beta_{k}^{-1}D
\end{align}
が得られます。この結果を利用して$\ln \rho_{nk}$を計算すると,
\ln \rho_{nk} &= E[\ln \pi_k] + \frac{1}{2} E[\ln |\mSigma_k|]-\frac{D}{2} \ln (2\pi) \notag \\[0.7em]
&\quad\quad-\frac{1}{2} E_{\vmu_k, \mSigma_k} \left[ (\vx_n-\vmu_k)^T \mSigma_k (\vx_n-\vmu_k) \right] \\[0.7em]
&= { \psi (\alpha_k)-\psi \left( \sum_{k=1}^{K} \alpha_k \right) } \notag \\[0.7em]
&\quad\quad + \frac{1}{2} { \sum_{i=1}^{D} \psi \left( \frac{\nu_k + 1-i}{2} \right) + D \ln (2) + \ln |\mW_k| } \notag \\[0.7em]
&\quad\quad-\frac{1}{2} \left\{\nu_{k}(\vx_n-\vm_k)^T \mW_k(\vx_n-\vm_k) + \beta_{k}^{-1}D \right\} \\[0.7em]
&= \ln \tilde{\pi}_k + \ln \tilde{\Sigma}_k-\frac{1}{2}\left\{\nu_k(\vx_n-\vm_k)^T \mW_k(\vx_n-\vm_k) + \beta_{k}^{-1}D \right\} \label{eq_ln_rho}
\end{align}
が得られます。ただし,ごちゃごちゃした項は以下のように置き換えました。
\ln \tilde{\pi}_k &= E[\ln \pi_k] \\[0.7em]
&= \psi (\alpha_k)-\psi \left( \sum_{k=1}^{K} \alpha_k \right) \\[0.7em]
\ln \tilde{\Sigma}_k &= \frac{1}{2}E[\ln |\mSigma_k|] \\[0.7em]
&= \sum_{i=1}^{D} \psi\left( \frac{\nu_k + 1-i}{2} \right) + D \ln (2) + \ln |\mW_k|
\end{align}
変分ベイズのEステップでは,この$\rho_{nk}$を計算して$r_{nk}$を求めます。そのために,ダイレクトに$r_{nk}$を更新できるような式を求めておきましょう。式($\ref{eq_ln_rho}$)の定義から$\rho_{nk}$を求めます。$\rho_{nk}$さえ求まれば,あとは正規化するだけで負担率$r_{nk}$が計算できます。
\rho_{nk} &= \exp \left[ \ln \tilde{\pi}_k + \frac{1}{2}\ln \tilde{\mSigma}_k-\frac{1}{2} \left\{\nu_k(\vx_n - \vm_k)^T \mW_k(\vx_n - \vm_k) + \beta_{k}^{-1}D \right\} \right] \\[0.7em]
&= \tilde{\pi}_k \tilde{\mSigma}_k ^{\frac{1}{2}} \exp \left\{-\frac{\nu_k}{2}(\vx_n - \vm_k)^T \mW_k(\vx_n - \vm_k) -\frac{D}{2 \beta_k} \right\}
\end{align}
以上で,「3. 更新式適用による変分下限の最大化」における変分Eステップの導出が完了しました。
変分Mステップ
続いて,パラメータに関する最適化を行う変分Mステップの導出を行います。Mステップでは,変分ベイズの更新式を用いて潜在変数以外のパラメータに関して最適化を施していきます。変分ベイズの更新式を利用するためには,$\vpi, \vmu, \mSigma$の対数同時分布$\ln p(\vpi, \vmu, \mSigma)$を知る必要があります。「1. 同時分布の依存関係確認」の仮定に基づくと,$\ln p(\vpi, \vmu, \mSigma)$は以下のように表されます。
\ln p(\vpi, \vmu, \mSigma) &= \ln p(\mX | \mZ, \vmu, \mSigma) + \ln p(\mZ | \vpi) + \ln p(\vpi) + \ln p(\vmu | \mSigma) + \ln p(\mSigma)
\end{align}
したがって,変分ベイズの更新式を用いると,$\vpi, \vmu, \mSigma$に関する近似事後分布は以下のように求められます。
\ln q^{\ast} (\vpi, \vmu, \mSigma)
&= E_{\mZ} \left[ \ln p(\vpi, \vmu, \mSigma) \right] \\[0.7em]
&= \sum_{k=1}^{K} \sum_{n=1}^{N} E[z_{nk}] \ln \N (\vx_n | \vmu_k, \mSigma^{-1}) + E_{\mZ} \left[ \ln p(\mZ | \vpi) \right] \notag \\[0.7em]
&\quad\quad + \ln p(\vpi) + \sum_{k=1}^{K} \ln p(\vmu_k, \mSigma_k) + \const \label{eq_q_pi_mu_sigma}
\end{align}
以下では,$\vpi$と$\vmu, \mSigma$に分けて近似事後分布を導出したいと思います。方針としては,式($\ref{eq_q_pi_mu_sigma}$)において,$\vpi$に関わる部分と$\vmu, \mSigma$に関わる部分を別々に抽出します。ここで$\vpi$と$\vmu, \mSigma$を別々に考えるのは,「1. 同時分布の依存関係確認」の仮定に基づいています。グラフィカルモデルを見ても分かる通り,$\vmu, \mSigma$は依存関係にありますが,$\vpi$は孤立しています。
多項分布$p(\mZ | \vpi)$の共役事前分布としてディリクレ分布$p(\vpi)$を仮定していますので,$\vpi$に関する近似事後分布$q^{\ast} (\vpi)$もまたディリクレ分布の形になります。今回は対数近似事後分布を考えていますので,式($\ref{eq_q_pi_mu_sigma}$)の$\vpi$に関わる部分はディリクレ分布の対数を取った形になるはずです。したがって,ディリクレ分布の対数を取った理想の形と係数比較を行うことで,$\vpi$に関する近似事後分布を求めることができます。
$\vmu, \mSigma$も同様に導出します。多変量正規分布$p(\mX | \mZ, \vmu, \mSigma)$の共役事前分布としてガウスウィシャート分布$p(\vmu | \mSigma)p(\mSigma)$を仮定していますので,近似事後分布$q^{\ast} (\vmu | \mSigma)$は多変量ガウス分布,$q^{\ast} (\mSigma)$はウィシャート分布になるはずです。したがって,多変量正規分布・ウィシャート分布の対数を取った理想の形と係数比較を行うことで,$\vmu, \mSigma$に関する近似事後分布を求めることができます。
早速,式($\ref{eq_q_pi_mu_sigma}$)において$\vpi$に関わる部分を抽出します。
\ln q^{\ast}(\vpi)
&= \sum_{k=1}^{K} \sum_{n=1}^{N} r_{nk} \ln \pi_k -\ln\left\{B(\valpha_0) \prod_{k=1}^{K} \pi_k ^{\alpha_0-1}\right\} + \const \\[0.7em]
&= \sum_{k=1}^{K} \sum_{n=1}^{N} r_{nk} \ln \pi_k + \sum_{k=1}^{K} (\alpha_0-1)\ln\pi_{k} + \const\\[0.7em]
&= \sum_{k=1}^{K}\left(\alpha_0-1+\sum_{n=1}^{N} r_{nk}\right)\ln \pi_k + \const
\end{align}
ただし,ディリクレ分布のパラメータ$\valpha_0$について,$K$クラスの初期値の対称性を考えて全ての要素を$\alpha_{0}$としました。ここで,分かりやすさのため,
N_k &= \sum_{n=1}^{N} r_{nk} = \sum_{n=1}^{N} E[z_{nk}]
\end{align}
とおくと,以下のように$\ln q^{\ast}(\vpi)$をキレイな形に変形することができます。
\ln q^{\ast}(\vpi) &= \sum_{k=1}^{K}(\alpha_0-1+N_k)\ln \pi_k + \const
\end{align}
先ほどもお伝えした通り,この形はディリクレ分布の対数をとったものになっているはずです。
\ln q^{\ast}(\vpi) &= \ln \Dir (\vpi | \valpha) = \sum_{k=1}^{K}(\alpha_k-1+N_k)\ln \pi_k + \const
\end{align}
すると,以下の恒等式が成り立ちます。
\sum_{k=1}^{K}(\alpha_0+N_k-1)\ln \pi_k &= \sum_{k=1}^{K} (\alpha_k-1)\ln \pi_k
\end{align}
係数比較により,$\alpha_k$に関する更新式が得られます。
\alpha_k &= \alpha_0 + N_k \label{eq_alpha_k}
\end{align}
これにて,$\vpi$に関する最適化は終了です。続いて,$\vmu, \mSigma$に関する最適化を行います。式($\ref{eq_q_pi_mu_sigma}$)において,$\vmu, \mSigma$に関わる部分を抽出します。
\ln q^{\ast} (\vmu, \mSigma)
&= \sum_{k=1}^{K} \ln \N (\vmu | \vm_0, (\beta_0 \mSigma_k)^{-1}) + \sum_{k=1}^{K} \ln \W (\mSigma_k | \mW_0, \nu_0) \notag \\[0.7em]
&\quad\quad + \sum_{n=1}^{N} \sum_{k=1}^{K} E[z_{nk}] \ln \N (\vx_n | \vmu_k, \mSigma_k^{-1}) + \const \\[0.7em]
&\propto \sum_{k=1}^{K} \left\{ \frac{1}{2} \ln | \beta_0 \mSigma_k|-\frac{1}{2} (\vmu_k-\vm_0)^T \beta_0 \mSigma_k (\vmu_k-\vm_0) \right. \notag \\[0.7em]
&\quad\quad + \frac{\nu_0-D-1}{2} \ln |\mSigma_k|-\frac{1}{2} \Tr( \mW_0^{-1} \mSigma_k) \notag \\[0.7em]
&\quad\quad + \left. \frac{1}{2} N_k \ln |\mSigma_k|-\frac{1}{2} \sum_{n=1}^{N} r_{nk} (\vx_n-\vmu_k)^T \mSigma_k (\vx_n-\vmu_k) \right\} \label{eq_q_ast_mu_sigma}
\end{align}
ここで注意するべきなのは,最後の項で早とちりして$\sum_{n=1}^{N}r_{nk}=N_k$と変形しないことです。なぜなら,$\sum_n$の中身に$\vx_n$が含まれているため,$N_k$の定義とは一致しないからです。ここは,引っかかりポイントだと思います。
さて,ここからはグラフィカルモデルに基づいて$\vmu$と$\mSigma$の依存関係を明確にしましょう。$\vmu$は$\mSigma$に依存していますから,ベイズの定理より$q^{\ast} (\vmu, \mSigma)$は理想的には以下のように分解されます。
q^{\ast} (\vmu, \mSigma) &= q^{\ast} (\vmu | \mSigma) q^{\ast} (\mSigma)
\end{align}
両辺の対数を取ります。
\ln q^{\ast} (\vmu, \mSigma) &= \ln q^{\ast} (\vmu | \mSigma) + \ln q^{\ast} (\mSigma) \label{eq_q_ast_mu_sigma_decompose}
\end{align}
したがって,式($\ref{eq_q_ast_mu_sigma}$)において$\vmu$に関する項だけを抽出した結果は$\ln q^{\ast} (\vmu | \mSigma)$となることが分かります。
&\ln q^{\ast} (\vmu|\mSigma) \notag \\[0.7em]
&\quad = -\frac{1}{2} \sum_{k=1}^{K} \left\{(\vmu_k-\vm_0)^T \beta_0 \mSigma_k (\vmu_k-\vm_0)+N_k (\vx_n-\vmu_k)^T \mSigma_k (\vx_n-\vmu_k) \right\}
\end{align}
先ほどもお伝えした通り,この形は多変量正規分布の対数をとったものになっているはずです。
\ln q^{\ast} (\vmu|\mSigma) &= \sum_{k=1}^{K}\ln \N (\vmu_k | \vm_k, \beta_k \mSigma_k) \\[0.7em]
&=\sum_{k=1}^{K}\left\{-\frac{1}{2}|\mSigma_k|-\frac{\beta_k}{2} (\vmu_k - \vm_k)^T \mSigma_k (\vmu_k-\vm_k) + \const\right\} \label{eq_q_ast_mu_given_sigma}
\end{align}
$\vpi$のときと同様に,式($\ref{eq_q_ast_mu_sigma}$)と式($\ref{eq_q_ast_mu_given_sigma}$)の恒等式から係数比較により更新式を導出していきます。そこで,一旦指数部の$\vmu_k^T \vmu_k$の項だけに注目して係数比較を行ってみましょう。式($\ref{eq_q_ast_mu_sigma}$)において,$\vmu_k^T \vmu_k$に関する項は以下です。
\vmu_k^T \beta_0 \mSigma_k \mu_k + N_k \vmu_k^T \mSigma_k \vmu_k
&= \vmu_k^T (\beta_0 + N_k)\mSigma_k \vmu_k
\end{align}
式($\ref{eq_q_ast_mu_given_sigma}$)において,$\vmu_k^T \vmu_k$に関する項は以下です。
\vmu_k^T \beta_k \mSigma_k \vmu_k
\end{align}
したがって,$\vmu_k$の二次の項である$\vmu_k^T \vmu_k$に着目すると,以下の恒等式が成り立ちます。
\vmu_k^T (\beta_0 + N_k)\mSigma_k \vmu_k &= \vmu_k^T (\beta_k)\mSigma_k \vmu_k
\end{align}
係数比較により,$\beta_k$に関する更新式が得られます。
\beta_k &= \beta_0 + N_k \label{eq_beta_k}
\end{align}
$\alpha_k$に関する更新式($\ref{eq_alpha_k}$)と対称的な結果が得られて美しいですね。しかし,まだ$\vm_k$に関する更新式が得られていません。そこで,指数部の$\vmu_k$の一次の項だけに注目して係数比較を行ってみましょう。式($\ref{eq_q_ast_mu_sigma}$)において,$\vmu_k$に関する項は以下です。
\vmu_k^T \beta_0 \mSigma_k \boldsymbol{m}_0 + \sum_{n=1}^{N} r_{nk} \vmu_k^T \mSigma_k \vx_n
&= \vmu_k^T \mSigma_k \left( \beta_0 m_0 + N_k \overline{\vx}_k \right)
\end{align}
式($\ref{eq_q_ast_mu_given_sigma}$)において,$\vmu_k$に関する項は以下です。
\vmu_k^T \mSigma_k \beta_0 \vm_k
\end{align}
したがって,以下の恒等式が成り立ちます。
\beta_k \vm_k &= \beta_0 \vm_0 + N_k \overline{\vx}_k
\end{align}
係数比較により,$\vm_k$に関する更新式が得られます。
\vm_k &= \frac{1}{\beta_k} \left( \beta_0 \vm_0 + N_k \overline{\vx}_k \right) \label{eq_m_k}
\end{align}
最後に,$\mSigma$に関する更新式を導出していきたいと思います。式($\ref{eq_q_ast_mu_sigma_decompose}$)を変形すると,$\ln q^{\ast}(\mSigma)$は以下のように表されます。
\ln q^{\ast} (\mSigma) &= \ln q^{\ast} (\vmu, \mSigma)-\ln q^{\ast} (\vmu | \mSigma) \label{q_ast_sigma}
\end{align}
式($\ref{eq_q_ast_mu_sigma}$)と式($\ref{eq_q_ast_mu_given_sigma}$)から式($\ref{q_ast_sigma}$)を計算していきます。
\ln q^{\ast} (\mSigma) &=
\sum_{k=1}^{K} \left\{ \frac{1}{2} \ln | \beta_0 \mSigma_k|-\frac{1}{2} (\vmu_k-\vm_0)^T \beta_0 \mSigma_k (\vmu_k-\vm_0) \right. \notag \\[0.7em]
&\quad\quad + \frac{\nu_0-D-1}{2} \ln |\mSigma_k|-\frac{1}{2} \Tr( \mW_0^{-1} \mSigma_k) \notag \\[0.7em]
&\quad\quad + \left. \frac{1}{2} N_k \ln |\mSigma_k|-\frac{1}{2} \sum_{n=1}^{N} r_{nk} (\vx_n-\vmu_k)^T \mSigma_k (\vx_n-\vmu_k) \right. \notag \\[0.7em]
&\quad\quad +\left. \frac{1}{2}|\mSigma_k|+\frac{\beta_k}{2} (\vmu_k - \vm_k)^T \mSigma_k (\vmu_k-\vm_k) + \const \right\} \label{eq_q_ast_sigma}
\end{align}
先ほどもお伝えした通り,この形はウィシャート分布の対数をとったものになっているはずです。
\ln q^{\ast} (\mSigma) &= \sum_{k=1}^{K} \left( \frac{\nu_k-D-1}{2} \ln |\mSigma_k|-\frac{1}{2} \Tr[\mW_k^{-1}\mSigma_k] \right) \label{eq_log_wishart}
\end{align}
$\ln |\Sigma_k|$に注目すると,以下の恒等式が成り立ちます。
\frac{\nu_0-D-1}{2} \ln |\mSigma_k| &= \frac{\nu_k-D-1}{2} \ln |\mSigma_k|
\end{align}
係数比較により,$\nu_k$に関する更新式が得られます。
\nu_k &= \nu_0 + N_k
\end{align}
$\alpha_k$に関する更新式($\ref{eq_alpha_k}$),$\beta_k$に関する更新式($\ref{eq_beta_k}$)と対称的な結果が得られて美しいですね。しかし,まだ$\mW_k$に関する更新式が得られていないため恒等式を立てます。ここでは,トレースに関する以下の3つの性質を利用します。
\vx^T A \vx &= \Tr \left[ A \vx \vx^T \right] \\[0.7em]
\Tr \left[ A \right] + \Tr \left[ B \right] &= \Tr \left[ A + B \right] \\[0.7em]
\Tr \left[ A^T \right] &= \Tr \left[ A \right]
\end{align}
上から順番に,トレースと二次形式の関係,トレースの線形性,トレースと転置の関係を表しています。これらの性質を念頭に置くと,式($\ref{eq_q_ast_sigma}$)における$\mSigma_k$に関する項は以下のように整理されます。
&-\frac{1}{2} \sum_{k=1}^K\Biggl\{ \Tr\left[\beta_0\mSigma_k(\vmu_k-\vm_0)(\vmu_k-\vm_0)^T\right] + \Tr \left[\mW_0^{-1} \mSigma_k \right] \notag \\[0.7em]
&\quad\quad \left. + \Tr \left[ \sum_{n=1}^{N}r_{nk}\mSigma_k(\vx_n-\vmu_k)(\vx_n-\vmu_k)^T \right]-\Tr \left[ \beta_k\mSigma_k(\vmu_k-\vm_k)(\vmu_k-\vm_k)^T \right] \right\} \\[0.7em]
&=-\frac{1}{2} \sum_{k=1}^K \Tr \Biggl[\beta_0\mSigma_k(\vmu_k-\vm_0)(\vmu_k-\vm_0)^T + \mW_0^{-1} \mSigma_k \notag \\[0.7em]
&\quad\quad + \sum_{n=1}^{N}r_{nk}\mSigma_k(\vx_n-\vmu_k)(\vx_n-\vmu_k)^T-\beta_k\mSigma_k(\vmu_k-\vm_k)(\vmu_k-\vm_k)^T \biggr] \\[0.7em]
&=-\frac{1}{2} \sum_{k=1}^K \Tr \Biggl[\beta_0\mSigma_k(\vmu_k-\vm_0)(\vmu_k-\vm_0)^T + \mSigma_k\mW_0^{-1} \notag \\[0.7em]
&\quad\quad + \sum_{n=1}^{N}r_{nk}\mSigma_k(\vx_n-\vmu_k)(\vx_n-\vmu_k)^T-\beta_k\mSigma_k(\vmu_k-\vm_k)(\vmu_k-\vm_k)^T \biggr]
\end{align}
ただし,$\mW_{0}$と$\mSigma_k$はどちらも対称行列であることを利用しました。一方,式($\ref{eq_log_wishart}$)における$\mSigma_k$に関する項も,トレースの転置に関する性質を利用すると以下のように整理することができます。
-\frac{1}{2} \sum_{k=1}^{K} \Tr \left[ \mW_k^{-1} \mSigma_k \right] &= -\frac{1}{2} \sum_{k=1}^{K} \Tr \left[ \mSigma_k\mW_k^{-1} \right]
\end{align}
したがって,得られる恒等式は以下のようになります。
\mSigma_k \mW_k^{-1} &=
\beta_0\mSigma_k(\vmu_k-\vm_0)(\vmu_k-\vm_0)^T + \mSigma_k\mW_0^{-1} \notag \\[0.7em]
&\quad\quad + \sum_{n=1}^{N}r_{nk}\mSigma_k(\vx_n-\vmu_k)(\vx_n-\vmu_k)^T-\beta_k\mSigma_k(\vmu_k-\vm_k)(\vmu_k-\vm_k)^T
\end{align}
両辺の左から$\mSigma_k^{-1}$を掛けると,$\mW_k$に関する以下の更新式が得られます。
\mW_k^{-1} &= \mW_0^{-1} + \beta_0(\vmu_k-\vm_0)(\vmu_k-\vm_0)^T \notag \\[0.7em]
&\quad\quad + \sum_{n=1}^{N}r_{nk}(\vx_n-\vmu_k)(\vx_n-\vmu_k)^T-\beta_k(\vmu_k-\vm_k)(\vmu_k-\vm_k)^T \label{eq_w_before_clean}
\end{align}
式($\ref{eq_w_before_clean}$)をキレイに表すために,以下のように新しい変数を導入します。
\overline{\vx}_k &= \frac{1}{N_k} \sum_{n=1}^{N} r_{nk} \vx_n \\[0.7em]
\mS_k &= \frac{1}{N_k} \sum_{n=1}^{N} r_{nk} (\vx_n-\overline{\vx}_k)(\vx_n-\overline{\vx}_k)^T
\end{align}
これらを利用して,式($\ref{eq_w_before_clean}$)を整理していきます。ポイントとなるのは,今回は$\ln q^{\ast}(\mSigma)$を考えていますので,$\vmu_k$の項は打ち消されるという点です。そこで,以下では$\vmu_k$の項を無視して考えていきます。式($\ref{eq_w_before_clean}$)を整理する際に必要となる計算を予め行っておきます。
\sum_{n=1}^{N} r_{nk}\vx_n \vx_n^T &= \sum_{n=1}^{N} r_{nk}(\vx_n-\overline{\vx}_k)(\vx_n-\overline{\vx}_k)^T \notag \\[0.7em]
&\quad\quad + 2 \sum_{n=1}^{N} r_{nk} \vx_n \overline{\vx}_k-\sum{n=1}^{N} r_{nk} \overline{\vx}_k \overline{\vx}_k^T \\[0.7em]
&= \sum_{n=1}^{N} r_{nk}(\vx_n-\overline{\vx}_k)(\vx_n - \overline{\vx}_k)^T + 2 N_k \overline{\vx}_k \overline{\vx}_k^T-\overline{\vx}_k \overline{\vx}_k^T \\[0.7em]
&= \sum_{n=1}^{N} r_{nk}(\vx_n-\overline{\vx}_k)(\vx_n-\overline{\vx}_k)^T + N_k \overline{\vx}_k \overline{\vx}_k^T \\[0.7em]
&= N_k \mS_k + N_k \overline{\vx}_k \overline{\vx}_k^T
\end{align}
式($\ref{eq_w_before_clean}$)を整理しましょう。$\beta_k$の更新式である式($\ref{eq_beta_k}$)と$\vm_k$の更新式である式($\ref{eq_m_k}$)を利用します。先ほどもお伝えしましたが,$\vmu_k$を含む項を無視するのがポイントです。
\mW_k^{-1} &= \mW_0^{-1} + \beta_0 \vm_0 \vm_0^T + \sum_{n=1}^N r_{nk} \vx_n \vx_n^T-\beta_k \vm_k \vm_k^T \\[0.7em]
&= \mW_0^{-1} + \beta_0 \vm_0 \vm_0^T + (N_k \mS_k + N_k \overline{\vx}_k \overline{\vx}_k^T)-\beta_k \vm_k \vm_k^T \\[0.7em]
&= \mW_0^{-1} + N_k \mS_k +\beta_0 \vm_0 \vm_0^T + N_k \overline{\vx}_k \overline{\vx}_k^T \notag \\[0.7em]
&\quad\quad-(\beta_0 + N_k) \cdot \frac{1}{(\beta_0 + N_k)^2}(\beta_0 \vm_0 + N_k \overline{\vx}_k) (\beta_0 \vm_0^T + N_k \overline{\vx}_k^T) \\[0.7em]
&= \mW_0^{-1} + N_k \mS_k + \frac{1}{\beta_0 + N_k} \left\{ (\beta_0 + N_k)(\beta_0 \vm_0 \vm_0^T + N_k \overline{\vx}_k \overline{\vx}_k^T) \right. \notag \\[0.7em]
&\quad\quad\left.-(\beta_0 \vm_0 + N_k \overline{\vx}_k)(\beta_0 \vm_0^T + N_k \overline{\vx}_k^T) \right\} \\[0.7em]
&= \mW_0^{-1} + N_k \mS_k + \frac{\beta_0 N_k}{\beta_0 + N_k} (\overline{\vx}_k-\vm_0)(\overline{\vx}_k-\vm_0)^T
\end{align}
$\beta_k = \beta_0 + N_k$ を利用すれば,$\vmu_k$の項が消えることを計算しても示すことができます。
以上で,潜在変数と全てのパラメータに関する更新式が得られました。改めて,変分ベイズのGMMへの適用の流れをまとめておきます。
変分ベイズのGMMへの適用(GMM-VB)は,以下の4ステップから構成される。
- 初期値設定
- 負担率$r_{nk}$の計算(変分Eステップ)
- 各パラメータの更新(変分Mステップ)
- 収束判定
まずは各パラメータに初期値$\alpha_0$,$\beta_0$,$\nu_0$,$\vm_0$,$\mW_0$を与える。次に,以下の変分Eステップと変分Mステップを収束するまで繰り返す。
変分Eステップ
負担率$r_{nk}$を計算する。
r_{nk} &= \frac{\rho_{nk}}{\sum_{j=1}^{K} \rho_{nj}}
\end{align}
ただし,$\rho_{nk}$は以下で計算できる。
\ln \tilde{\pi}_k &= \psi (\alpha_k)-\psi \left( \sum_{k=1}^{K} \alpha_k \right) \\[0.7em]
\ln \tilde{\Sigma}_k &= \sum_{i=1}^{D} \psi\left( \frac{\nu_k + 1-i}{2} \right) + D \ln (2) + \ln |\mW_k| \\[0.7em]
\rho_{nk} &= \tilde{\pi}_k \tilde{\mSigma}_k ^{\frac{1}{2}} \exp \left\{-\frac{D}{2 \beta_k}-\frac{\nu_k}{2}(\vx_n-\vm_k)^T \mW_k(\vx_n-\vm_k) \right\}
\end{align}
変分Mステップ
パラメータを更新する。
\alpha_k &= \alpha_0 + N_k \\[0.7em]
\beta_k &= \beta_0 + N_k \\[0.7em]
\nu_k &= \nu_0 + N_k \\[0.7em]
\vm_k &= \frac{1}{\beta_k} (\beta_0 \vm_0 + N_k \overline{\vx}_k) \\[0.7em]
\mW_k^{-1} &= \mW_0^{-1} + N_k \mS_k + \frac{\beta_0 N_k}{\beta_0 + N_k} (\overline{\vx}_k-\vm_0)(\overline{\vx}_k-\vm_0)^T
\end{align}
ただし,$N_k$,$\overline{\vx}_k$,$\mS_k$は変分Eステップで計算した負担率$r_{nk}$を用いて計算できる。
N_k &= \sum_{n=1}^{N} r_{nk} \\[0.7em]
\overline{\vx}_k &= \frac{1}{N_k} \sum_{n=1}^{N} r_{nk} \vx_n \\[0.7em]
\mS_k &= \frac{1}{N_k} \sum_{n=1}^{N} r_{nk} (\vx_n-\overline{\vx}_k) (\vx_n-\overline{\vx}_k)^T \\[0.7em]
\end{align}

以上で,変分ベイズのGMMへの適用は完了です。初期値の設定や収束判定は,実装の章で確認します。
ここまで読了された賢明な読者の皆さまはお気づきかもしれませんが,変分ベイズの欠点は更新式の導出が煩雑になることです。今回採り上げた混合ガウス分布は比較的単純なケースなのですが,それでも上で確認したように計算がかなり煩雑になってしまいます。このような背景から,ベイズモデリングの実際の応用ではマルコフ連鎖モンテカルロ法(Markov chain Monte Carlo methods: MCMC)などのサンプリング法が用いられることがあります。
実装
本章では,GMMを題材にEMアルゴリズムに基づくクラスタリングと変分ベイズに基づくクラスタリングの実装をお伝えしていきます。具体的には,10000個の3次元データをGMM-EM(EMアルゴリズムによる混合ガウス分布の推論)とGMM-VB(変分ベイズによる混合ガウス分布の推論)を利用してクラスタリングする実装例をお伝えしていきます。要するに,以下のパラメータを仮定します。
N &= 10000 \\[0.7em]
D &= 3
\end{align}
実装はGithubで公開しています。
ソースコードのコメントは英語で書いています。これはGithubで公開する際に,外国の方々にも参考にしていただきたいからです。コメント規則であるdocstringはGoogleスタイルを利用しています。
ここからは,以下の形式でメソッド単位で解説を行っていきます。
[メソッド名・その他タイトルなど]
# ソースコード[ソースコードの解説]
Github上のコードはDockerを用いて動かせるように整備していますが,下記のコードはGoogle Colaboratoryを用いて気軽に試せるようにしています。ぜひコードをコピペしてお試しください。
データの準備
以下では,GMM-EMとGMM-VBを適用するデータを生成していきます。
import sys # 引数の操作
import csv # csvの読み込み
import numpy as np # 数値計算
import matplotlib.pyplot as plt # 可視化
from numpy import linalg as la # 行列計算
from collections import Counter # 頻度カウント
from scipy.special import digamma, logsumexp # 数値計算
from scipy.stats import multivariate_normal # 多次元ガウス分布の確率密度関数の計算
from mpl_toolkits.mplot3d import Axes3D # 可視化標準的なライブラリをインポートします。
# 各クラスターに属するデータ数
# 今回は全てのクラスタでデータ数が同じと仮定する
# 全体のデータ数は N = N1 + N2 + N3 + N4 となる
# 各クラスタのデータ数
N1 = 4000
N2 = 3000
N3 = 2000
N4 = 1000
# 平均
Mu1 = [5, -5, -5]
Mu2 = [-5, 5, 5]
Mu3 = [-5, -5, -5]
Mu4 = [5, 5, 5]
# 共分散
Sigma1 = [[1, 0, -0.25], [0, 1, 0], [-0.25, 0, 1]]
Sigma2 = [[1, 0, 0], [0, 1, -0.25], [0, -0.25, 1]]
Sigma3 = [[1, 0.25, 0], [0.25, 1, 0], [0, 0, 1]]
Sigma4 = [[1, 0, 0], [0, 1, 0], [0, 0, 1]]
# 乱数を生成
X1 = np.random.multivariate_normal(Mu1, Sigma1, N1)
X2 = np.random.multivariate_normal(Mu2, Sigma2, N2)
X3 = np.random.multivariate_normal(Mu3, Sigma3, N3)
X4 = np.random.multivariate_normal(Mu4, Sigma4, N4)データを作成します。今回は4つのガウス分布からデータを生成しましょう。クラスタリングとしては非常に簡単な問題設定になっています。なお,以下で載せている画像は当サイトのカラーリストを利用していますが,今回お伝えする実装はtab10のcolormapを利用します。本質的には重要でない部分ですので,気にしなくても大丈夫です。
# 描画準備
fig = plt.figure(figsize=(4, 4), dpi=300)
ax = Axes3D(fig)
fig.add_axes(ax)
# 当サイトのカスタムカラーリスト
cm = plt.get_cmap("tab10")
# メモリを除去
ax.set_xticks([])
ax.set_yticks([])
ax.set_zticks([])
# 少し回転させて見やすくする
ax.view_init(elev=10, azim=70)
# 描画
ax.plot(X1[:,0], X1[:,1], X1[:,2], "o", ms=0.5, color=cm(0))
ax.plot(X2[:,0], X2[:,1], X2[:,2], "o", ms=0.5, color=cm(1))
ax.plot(X3[:,0], X3[:,1], X3[:,2], "o", ms=0.5, color=cm(2))
ax.plot(X4[:,0], X4[:,1], X4[:,2], "o", ms=0.5, color=cm(3))
plt.show()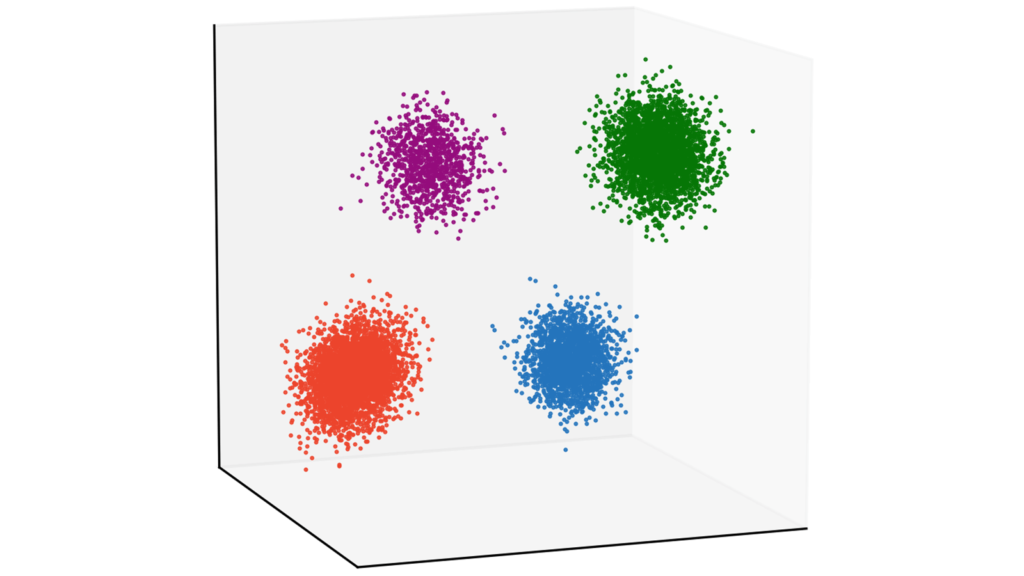
可視化して確認していきましょう。
# 4つのクラスを結合
X = np.concatenate([X1, X2, X3, X4])
# 描画準備
fig = plt.figure(figsize=(4, 4), dpi=300)
ax = Axes3D(fig)
fig.add_axes(ax)
# メモリを除去
ax.set_xticks([])
ax.set_yticks([])
ax.set_zticks([])
# 少し回転させて見やすくする
ax.view_init(elev=10, azim=70)
# 描画
ax.plot(X[:,0], X[:,1], X[:,2], "o", ms=0.5, color=cm(0))
plt.show()
今回は,4つのクラスラベルを排除したものをクラスタリング対象としますので,データを結合しましょう。
# csvでデータを保存
np.savetxt("data.csv", X, delimiter=",")毎回同じデータに対してクラスタリングを行うため,データをcsvに吐き出しておきます。当サイトのデモで利用しているcsvは以下でダウンロードできます。
# ご自身の環境におけるcsvへのパス
csv_dir = "[path to data.csv]"
# csvを読み取って(N, D)行列を生成
with open(csv_dir) as f:
reader = csv.reader(f)
X = [_ for _ in reader]
for i in range(len(X)):
for j in range(len(X[i])):
X[i][j] = float(X[i][j])
# 後のためにnumpy化しておく
X = np.array(X)当サイトと全く同じデータを利用したい場合は,上記ボタンからcsvをダウンロードしていただき,csvからデータを生成してください。ただし,[path to data.csv] にはご自身の環境におけるcsvファイルへのパスを挿入してください。この後から,EMアルゴリズムと変分ベイズで実装が分岐していきます。
EMアルゴリズム
GMMEMクラスの定義
詳しい実装内容は「EMアルゴリズムをはじめからていねいに」をご参照下さい。
GMMEMの実行
上で定義したGMMEMクラスのインスタンスを生成して,GMM-EMを実行しましょう。以下では,GMM-VBとの比較を行うためにいくつかの条件で実行してみます。
$K=4$の場合
# モデルをインスタンス化する
model = GMMEM(K=4)
# EMアルゴリズムを実行する
model.execute(X, iter_max=100, thr=0.001)クラスタ数$K$は$4$,最大更新回数は$100$回としました。収束判定における対数尤度増加幅の閾値は$0.001$としました。

しっかりとクラスタリングできていますね。ログを確認すると,更新回数は$10$回だったことが分かります。
Log-likelihood gap: 19.66
Log-likelihood gap: 11.95
Log-likelihood gap: 4.53
Log-likelihood gap: 0.04
Log-likelihood gap: 0.74
Log-likelihood gap: 0.57
Log-likelihood gap: 0.01
Log-likelihood gap: 2.94
Log-likelihood gap: 1.65
Log-likelihood gap: 0.0
EM algorithm has stopped after 10 iteraions.$K=8$の場合
# モデルをインスタンス化する
model = GMMEM(K=8)
# EMアルゴリズムを実行する
model.execute(X, iter_max=100, thr=0.001)クラスタ数$K$は$8$として,他のパラメータは先ほどと同様の設定で行いました。
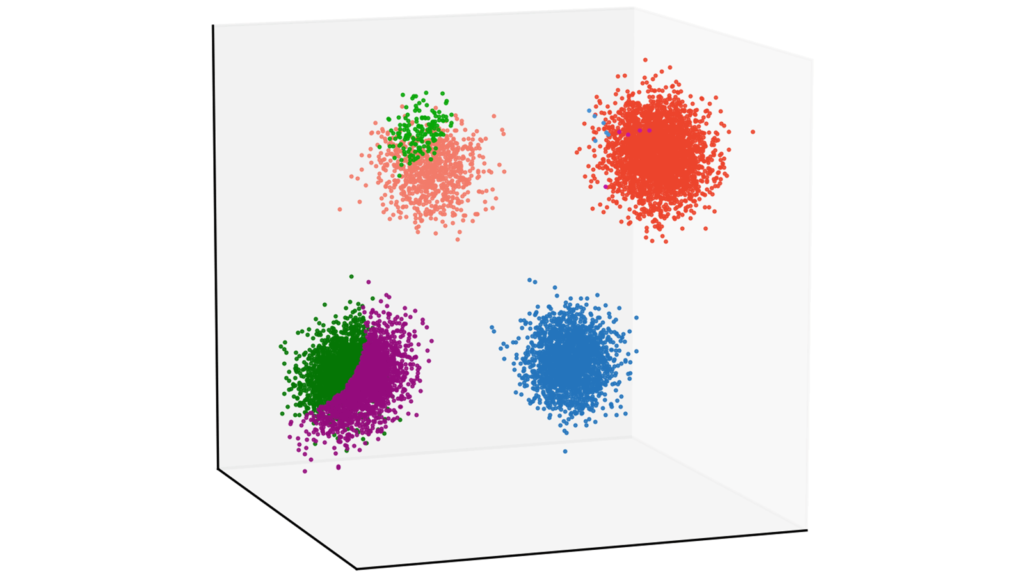
正しくクラスタリングされませんでした。ログを確認すると,更新回数は最大の$100$回となっていたため,うまく収束できなかったようです。点推定では,$4$つに分かれているクラスタを$K=8$の条件下では正しく推定できなかったということです。
Log-likelihood gap: 23.37
Log-likelihood gap: 8.06
Log-likelihood gap: 2.36
Log-likelihood gap: 3.5
Log-likelihood gap: 3.02
~~~~~~~~~~
省略
~~~~~~~~~~
Log-likelihood gap: 0.22
Log-likelihood gap: 0.2
Log-likelihood gap: 0.19
Log-likelihood gap: 0.18
Log-likelihood gap: 0.17
EM algorithm has stopped after 100 iteraions.データの中に実質的な情報が僅かしか含まれていない性質のことを「スパース性」と呼びます。今回の場合は,仮定したクラス数よりも実際に推定するクラス数の方が少なく,EMアルゴリズムがスパース性を考慮できなかったために,クラスラベルを正しく推定することができなかったと考えられます。変分ベイズでは,後に述べる「関連度自動決定」により,スパース性を担保したクラスタリングが可能になります。
変分ベイズ
GMMVBクラスの定義
class GMMVB():ここからは,GMMVBクラスを定義していきます。
コンストラクタ
def __init__(self, K):
"""コンストラクタ
Args:
K (int): クラスタ数
Returns:
None.
Note:
eps (float): オーバーフローとアンダーフローを防ぐための微小量
"""
self.K = K
self.eps = np.spacing(1) クラスタ数Kと微小量epsを定義します。epsは$0$除算を防ぐため等に利用します。
パラメータ初期化メソッド
def init_params(self, X):
"""パラメータ初期化メソッド
Args:
X (numpy ndarray): (N, D)サイズの入力データ
Returns:
None.
"""
# 入力データ X のサイズは (N, D)
self.N, self.D = X.shape
# スカラーのパラメータセット
self.alpha0 = 0.01
self.beta0 = 1.0
self.nu0 = float(self.D)
# 平均は標準ガウス分布から生成
self.m0 = np.random.randn(self.D)
# 分散共分散行列は単位行列
self.W0 = np.eye(self.D)
# 負担率は標準正規分布から生成するがEステップですぐ更新するので初期値自体には意味がない
self.r = np.random.randn(self.N, self.K)
# 更新対象のパラメータを初期化
self.alpha = np.ones(self.K) * self.alpha0
self.beta = np.ones(self.K) * self.beta0
self.nu = np.ones(self.K) * self.nu0
self.m = np.random.randn(self.K, self.D)
self.W = np.tile(self.W0[None,:,:], (self.K, 1, 1))| 変数 | サイズ | 意味 |
N | int | データ数 |
D | int | データの次元 |
alpha0 | float | ディリクレ分布のパラメータ初期値 |
beta0 | float | ガウス分布の分散共分散行列の係数初期値 |
nu0 | float | ウィシャート分布のパラメータ初期値 |
m0 | (K, D) | ガウス分布の平均 |
W0 | (K, D, D) | ガウス分布の分散共分散行列 |
r | (N, K) | 負担率 |
alpha | (K) | ディリクレ分布のパラメータ |
beta | (K) | ガウス分布の分散共分散行列の係数 |
nu | (K) | ウィシャート分布のパラメータ |
m | (N, D) | ガウス分布の平均 |
W | (K, D, D) | ウィシャート分布のパラメータ |
パラメータの初期化を行います。
ディリクレ分布パラメータ$\alpha_0$の初期値は$0.01$としました。$\alpha_0$は$\pi_k$の事前分布のパラメータですので,素朴に考えると$1/K$が適切のように思えますが,変分ベイズではスパース性を担保した推定が行えることから,初期値として小さな値を採用しています。
ガウス分布のパラメータ$\beta_0$の初期値は$1.0$としました。$\beta_0$は$\mSigma_k$のスケールを表していますので,初期値としては等倍である$1.0$を選択しました。
ウィシャート分布のパラメータ$\nu_0$の初期値は次元数$D$としました。上では指摘していませんが,ウィシャート分布における$\nu$は$D-1$よりも大きくなければいけません。$\nu_0$として$1.0$や$0$を与えてしまうと,推定が不安定な挙動を示してしまうため注意が必要です。
GMMの確率密度関数計算メソッド
def gmm_pdf(self, X):
"""N個のD次元データに対してGMMの確率密度関数を計算するメソッド
Args:
X (numpy ndarray): (N, D)サイズの入力データ
Returns:
Probability density function (numpy ndarray): 各クラスタにおけるN個のデータに関して計算するため出力サイズは (N, K) となる
"""
pi = self.alpha / (np.sum(self.alpha, keepdims=True) + np.spacing(1)) # (K)
return np.array([pi[k] * multivariate_normal.pdf(X, mean=self.m[k], cov=la.pinv(self.nu[:,None,None] * self.W)[k]) for k in range(self.K)]).T # (N, K)GMMの確率密度関数を計算します。EMアルゴリズムでは混合ガウス分布の混合率$\pi_k$・平均$\vmu_k$・分散共分散行列$\mSigma_k$は更新対象のパラメータでしたが,変分ベイズでは$\pi_k$・$\vmu_k$・$\mSigma_k$には事前分布を設定しているために,それら自体は更新対象のパラメータではありません。言い換えれば,現時点ではGMMの確率密度関数を計算するための$\pi_k$・$\vmu_k$・$\mSigma_k$が手に入っていないということです。
このような背景から,$\pi_k$・$\vmu_k$・$\mSigma_k$はそれぞれの事前分布から代表値を抽出してあげる必要があります。代表値として何を用いるのかは自明ではありませんが,ここでは単純に期待値を採用します。式($\ref{p_pi}$)と式($\ref{e_pi}$)より,$\vpi$の期待値はディリクレ分布の期待値になります。
E[\pi_k] &= \frac{\alpha_k}{\sum_{j=1}^{K} \alpha_j}
\end{align}
同様に,式($\ref{p_mu_sigma}$)と式($\ref{e_mu}$)より,$\vmu$の期待値はガウス分布の期待値になります。
E[\vmu_k] &= \vm_0
\end{align}
同様に,式($\ref{p_sigma}$)と式($\ref{e_sigma}$)より,$\mSigma$の期待値はウィシャート分布の期待値になります。
E[\mSigma_k] &= \nu_k \mW_k
\end{align}
これらの代表値を用いて,GMMの確率密度関数を計算します。計算自体はEMアルゴリズムと同様ですので,詳細は割愛します。
変分Eステップメソッド
def e_step(self, X):
"""変分Eステップを実行するメソッド
Args:
X (numpy ndarray): (N, D)サイズの入力データ
Returns:
None.
Note:
以下のフィールドが更新される
self.r (numpy ndarray): (N, K)サイズの負担率
"""
# rhoを求めるために必要な要素の計算
log_pi_tilde = (digamma(self.alpha) - digamma(self.alpha.sum()))[None,:] # (1, K)
log_sigma_tilde = (np.sum([digamma((self.nu + 1 - i) / 2) for i in range(self.D)]) + (self.D * np.log(2) + (np.log(la.det(self.W) + np.spacing(1)))))[None, :] # (1, K)
nu_tile = np.tile(self.nu[None,:], (self.N, 1)) # (N, K)
res_error = np.tile(X[:,None,None,:], (1, self.K, 1, 1)) - np.tile(self.m[None,:,None,:], (self.N, 1, 1, 1)) # (N, K, 1, D)
quadratic = nu_tile * ((res_error @ np.tile(self.W[None,:,:,:], (self.N, 1, 1, 1))) @ res_error.transpose(0,1,3,2))[:,:,0,0] # (N, K)
# 対数領域でrhoを計算
log_rho = log_pi_tilde + (0.5 * log_sigma_tilde) - (0.5 * self.D / (self.beta + np.spacing(1)))[None,:] - (0.5 * quadratic) # (N, K)
# logsumexp関数を利用して対数領域で負担率を計算
log_r = log_rho - logsumexp(log_rho, axis=1, keepdims=True) # (N, K)
# 対数領域から元に戻す
r = np.exp(log_r) # (N, K)
# np.expでオーバーフローを起こしている可能性があるためnanを置換しておく
r[np.isnan(r)] = 1.0 / (self.K) # (N, K)
self.r = r # (N, K)変分Eステップを実行します。具体的には,以下を計算した後に,
\ln \tilde{\pi}_k &= \psi (\alpha_k)-\psi \left( \sum_{k=1}^{K} \alpha_k \right) \\[0.7em]
\ln \tilde{\Sigma}_k &= \sum_{i=1}^{D} \psi\left( \frac{\nu_k + 1-i}{2} \right) + D \ln (2) + \ln |\mW_k| \\[0.7em]
\rho_{nk} &= \tilde{\pi}_k \tilde{\mSigma}_k ^{\frac{1}{2}} \exp \left\{-\frac{D}{2 \beta_k}-\frac{\nu_k}{2}(\vx_n-\vm_k)^T \mW_k(\vx_n-\vm_k) \right\} \label{vb_rho}
\end{align}
その結果を用いて以下を計算します。
r_{nk} &= \frac{\rho_{nk}}{\sum_{j=1}^{K} \rho_{nj}}
\end{align}
EMアルゴリズム同様,オーバーフローを防ぐために対数領域で計算を行います。早速,負担率の対数を取ってみましょう。
\ln r_{nk} &= \ln \rho_{nk}-\ln \sum_{j=1}^{K} \rho_{nj} \label{vb_log_r}
\end{align}
EMアルゴリズム同様,$\ln \rho_{nk}$の計算は行列演算を用いて高速化を図ります。
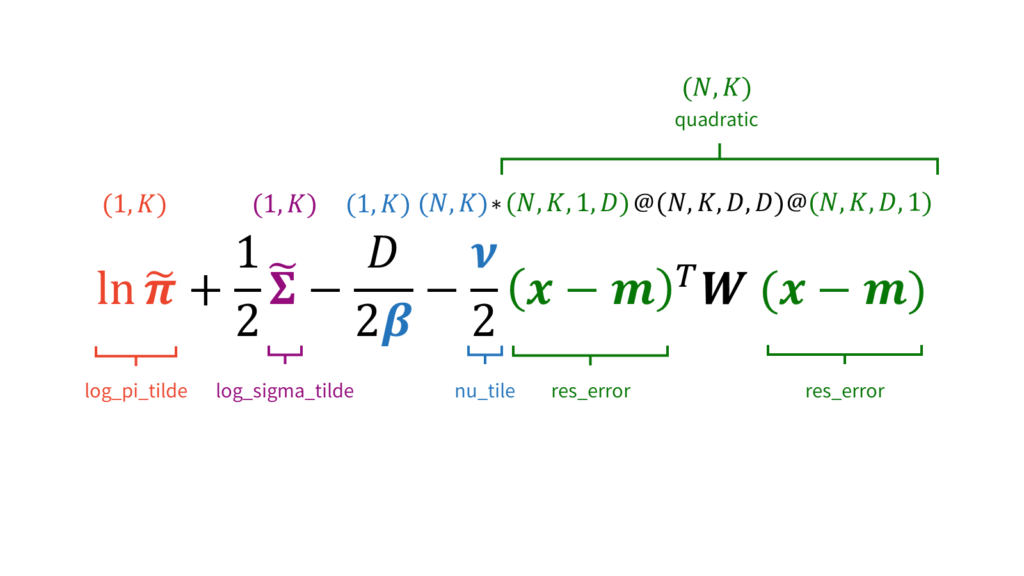
$(1, K)$と$(N, K)$同士の和算・減算がありますが,ここでは$(1, K)$側を自動で$(N, K)$側に揃えてくれるブロードキャストというnumpyの機能を利用します。
改めて式($\ref{vb_rho}$)をみると,第二項目に対数領域ではない$\rho_{nk}$が含まれています。$\rho_{nk}$には指数演算が含まれていますので,$\rho_{nk}$自体の計算は対数領域で行ったうえで,一番最後に指数演算を施して元に戻してあげた方がベターです。オーバーフローのリスクはなるべく一か所に集中させてあげた方が良いという思想です。
そこで,以下の変形を無理やり行うことで,第二項目でも$\ln \rho_{nk}$を利用して計算を行うことが可能になります。
\ln r_{nk} &= \ln \rho_{nk}-\ln \sum_{j=1}^{K} \exp \left( \ln \rho_{nj} \right) \label{vb_log_rho}
\end{align}
ここで,第二項目に現れた$\ln \sum \exp$はscipy.specialのlogsumexpというモジュールを利用することができます。
logsumexpは対数領域で計算を行う場合によく出現する項です。今回のケースのように,オーバーフローを防ぐための施策として頻繁に用いられる汎用的な手法ですので,ここでおさえておくとよいでしょう。
Mステップメソッド
def m_step(self, X):
"""変分Mステップを実行するメソッド
Args:
X (numpy ndarray): (N, D)サイズの入力データ
Returns:
None.
Note:
以下のフィールドが更新される
self.alpha (numpy ndarray): (K) サイズのディリクレ分布のパラメータ
self.beta (numpy ndarray): (K) ガウス分布の分散共分散行列の係数
self.nu (numpy ndarray): (K) サイズのウィシャート分布のパラメータ
self.m (numpy ndarray): (K, D) サイズの混合ガウス分布の平均
self.W (numpy ndarray): (K, D, D) サイズのウィシャート分布のパラメータ
"""
# 各パラメータを求めるために必要な要素の計算
N_k = np.sum(self.r, 0) # (K)
r_tile = np.tile(self.r[:,:,None], (1, 1, self.D)).transpose(1, 2, 0) # (K, D, N)
x_bar = np.sum((r_tile * np.tile(X[None,:,:], (self.K, 1, 1)).transpose(0,2,1)), 2) / (N_k[:,None] + np.spacing(1)) # (K, D)
res_error = np.tile(X[None,:,:], (self.K, 1, 1)).transpose(0,2,1) - np.tile(x_bar[:,:,None], (1, 1, self.N)) # (K, D, N)
S = ((r_tile * res_error) @ res_error.transpose(0,2,1)) / (N_k[:,None,None] + np.spacing(1)) # (K, D, D)
res_error_bar = x_bar - np.tile(self.m0[None,:], (self.K, 1)) # (K, D)
# 各パラメータを更新
self.alpha = self.alpha0 + N_k #(K)
self.beta = self.beta0 + N_k #(K)
self.nu = self.nu0 + N_k #(K)
self.m = (np.tile((self.beta0 * self.m0)[None,:], (self.K, 1)) + (N_k[:, None] * x_bar)) / (self.beta[:,None] + np.spacing(1)) # (K, D)
W_inv = la.pinv(self.W0) + (N_k[:,None,None] * S) + (((self.beta0 * N_k)[:,None,None] * res_error_bar[:,:,None] @ res_error_bar[:,None,:]) / (self.beta0 + N_k)[:,None,None] + np.spacing(1)) # (K, D, D)
self.W = la.pinv(W_inv) # (K, D, D)変分Mステップを実行します。変分EステップはEMアルゴリズムと同様に負担率を求めるだけでしたので,負担率の計算方法を除いて特に変わりはありませんでした。一方で,変分Mステップでは更新対象のパラメータがごっそり変わるため実装もかなり変わってきます。具体的には,以下を計算した後に,
N_k &= \sum_{n=1}^{N} r_{nk} \\[0.7em]
\overline{\vx}_k &= \frac{1}{N_k} \sum_{n=1}^{N} r_{nk} \vx_n \\[0.7em]
\mS_k &= \frac{1}{N_k} \sum_{n=1}^{N} r_{nk} (\vx_n-\overline{\vx}_k) (\vx_n-\overline{\vx}_k)^T \\[0.7em]
\end{align}
その結果を用いて以下を計算します。
\alpha_k &= \alpha_0 + N_k \\[0.7em]
\beta_k &= \beta_0 + N_k \\[0.7em]
\nu_k &= \nu_0 + N_k \\[0.7em]
\vm_k &= \frac{1}{\beta_k} (\beta_0 \vm_0 + N_k \overline{\vx}_k) \\[0.7em]
\mW_k^{-1} &= \mW_0^{-1} + N_k \mS_k + \frac{\beta_0 N_k}{\beta_0 + N_k} (\overline{\vx}_k-\vm_0)(\overline{\vx}_k-\vm_0)^T \label{vb_w}
\end{align}
EMアルゴリズム同様,$\mS_k$の計算は行列演算を用いて高速化を図ります。
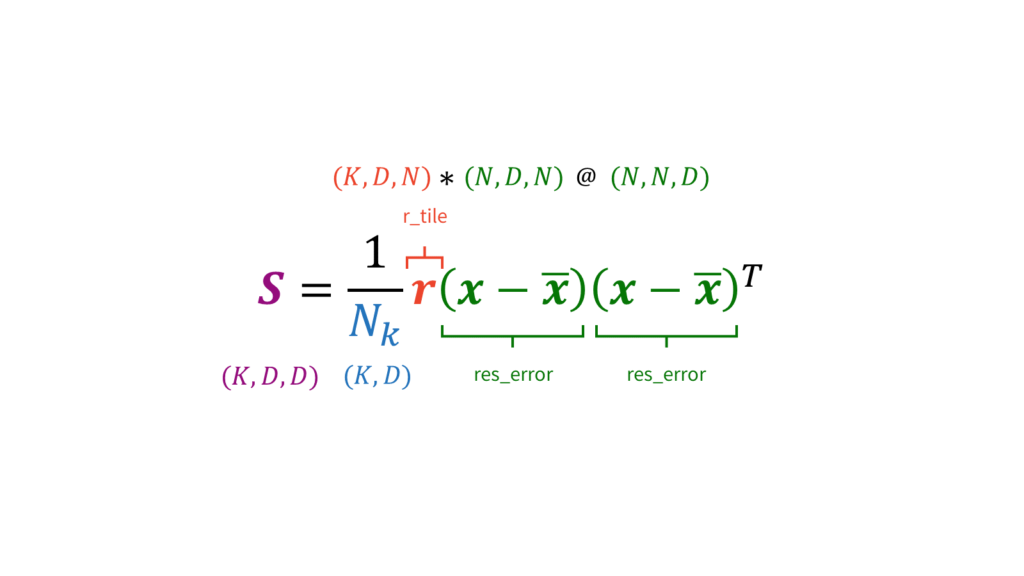
同様に,$\mW^{-1}_k$の計算も行列演算を用いて高速化を図ります。
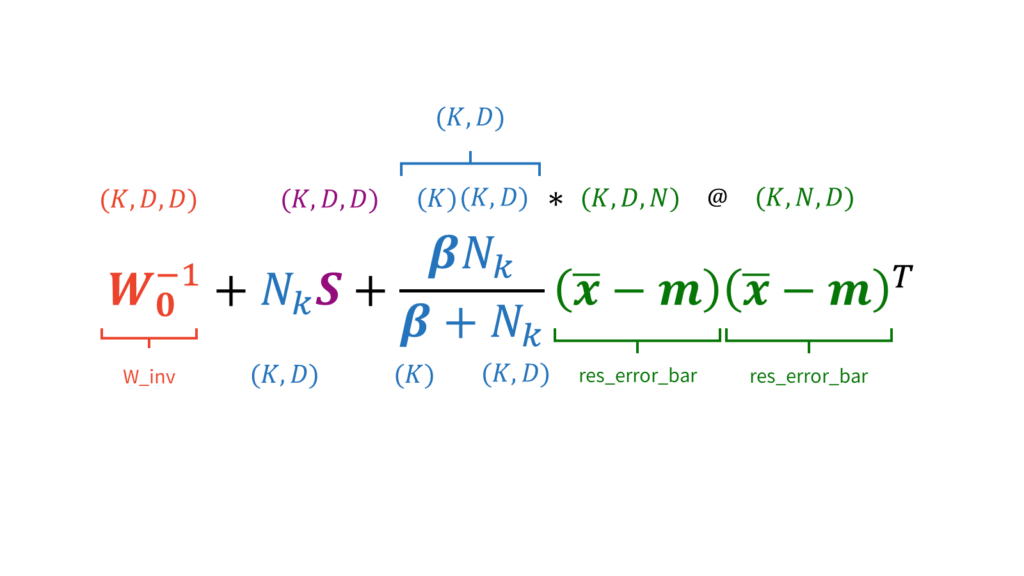
注意が必要なのは,フィールドではself.Wを逆行列として定めていないという点です。式($\ref{vb_w}$)は逆行列$\mW^{-1}$に対する更新式ですので,self.Wをアップデートする際は逆行列にしてあげる必要があります。
逆行列の計算ですが,la.invを利用すると行列が正則でない場合に逆行列が計算できずにエラーが出てしまいます。そこで,正則でない行列に対しても逆行列(に似た性質の行列)を計算できるla.pinvを利用します。また,除算を行う際は0除算を防ぐために微小量epsを分母に加算していることに注意してください。
可視化メソッド
def visualize(self, X):
"""可視化を実行するメソッド
Args:
X (numpy ndarray): (N, D)サイズの入力データ
Returns:
None.
Note:
このメソッドでは plt.show が実行されるが plt.close() は実行されない
"""
# クラスタリングを実行
labels = np.argmax(self.r, 1) # (N)
# 利用するカラーを極力揃えるためクラスタを出現頻度の降順に並び替える
label_frequency_desc = [l[0] for l in Counter(labels).most_common()]
# tab10 カラーマップを利用
cm = plt.get_cmap("tab10")
# 描画準備
fig = plt.figure(figsize=(4, 4), dpi=300)
ax = Axes3D(fig)
fig.add_axes(ax)
# メモリを除去
ax.set_xticks([])
ax.set_yticks([])
ax.set_zticks([])
# 少し回転させて見やすくする
ax.view_init(elev=10, azim=70)
# 各クラスタごとに可視化を実行する
for k in range(len(label_frequency_desc)):
cluster_indexes = np.where(labels==label_frequency_desc[k])[0]
ax.plot(X[cluster_indexes, 0], X[cluster_indexes, 1], X[cluster_indexes, 2], "o", ms=0.5, color=cm(k))
plt.show()VBが収束した後に,各クラスごとに色分けした可視化を行い結果を確認します。EMアルゴリズムと全く同じメソッドです。
実行メソッド
def execute(self, X, iter_max, thr):
"""VBを実行するメソッド
Args:
X (numpy ndarray): (N, D)サイズの入力データ
iter_max (int): 最大更新回数
thr (float): 更新停止の閾値 (対数尤度の増加幅)
Returns:
None.
"""
# パラメータ初期化
self.init_params(X)
# 各イテレーションの対数尤度を記録するためのリスト
log_likelihood_list =[]
# 対数尤度の初期値を計算
log_likelihood_list.append(np.mean(np.log(np.sum(self.gmm_pdf(X), 1) + self.eps)))
# 更新開始
for i in range(iter_max):
# Eステップの実行
self.e_step(X)
# Mステップの実行
self.m_step(X)
# 今回のイテレーションの対数尤度を記録する
log_likelihood_list.append(np.mean(np.log(np.sum(self.gmm_pdf(X), 1) + self.eps)))
# 前回の対数尤度からの増加幅を出力する
print("Log-likelihood gap: " + str(round(np.abs(log_likelihood_list[i] - log_likelihood_list[i+1]), 2)))
# もし収束条件を満たした場合,もしくは最大更新回数に到達した場合は更新停止して可視化を行う
if (np.abs(log_likelihood_list[i] - log_likelihood_list[i+1]) < thr) or (i == iter_max - 1):
print(f"VB has stopped after {i + 1} iteraions.")
self.visualize(X)
break今まで定義してきたメソッドを駆使して,GMM-VBを実行します。初期化,変分Eステップ,変分Mステップ,収束判定と繰り返すことで,パラメータを更新していきます。収束判定では,「閾値」もしくは「最大更新回数」のいずれかが引っかかった場合に更新をストップするようにしています。EMアルゴリズム同様,閾値判定に用いる対数尤度は,全てのデータ点の和ではなく平均を利用しています。結局,EMアルゴリズムと全く同じメソッドです。
EMアルゴリズムの目的関数は対数尤度でしたので,収束条件に対数尤度を設定するのは合理的です。一方で,変分ベイズの目的関数はKLダイバージェンスもしくは下限でしたので,収束条件に対数尤度を設定するのは一見合理的ではありません。しかし,対数尤度が「パラメータが与えられたときの観測データの尤もらしさ」を表すことを踏まえれば,変分ベイズでも収束条件に対数尤度を設定するのは十分合理的です。
GMMVBの実行
上で定義したGMMVBクラスのインスタンスを生成して,GMM-VBを実行しましょう。以下では,GMM-VBとの比較を行うためにいくつかの条件で実行してみます。
$K=4$の場合
# モデルをインスタンス化する
model = GMMVB(K=4)
# VBを実行する
model.execute(X, iter_max=100, thr=0.001)クラスタ数$K$は$4$,最大更新回数は$100$回としました。収束判定における対数尤度の増加幅の閾値は$0.001$としました。

しっかりとクラスタリングできていますね。ログを確認すると,更新回数は$10$回だったことが分かります。
Log-likelihood gap: 28.41
Log-likelihood gap: 0.08
Log-likelihood gap: 0.05
Log-likelihood gap: 0.01
Log-likelihood gap: 0.01
Log-likelihood gap: 0.03
Log-likelihood gap: 0.07
Log-likelihood gap: 0.14
Log-likelihood gap: 0.07
Log-likelihood gap: 0.0
VB has stopped after 10 iteraions.$K=8$の場合
# モデルをインスタンス化する
model = GMMVB(K=8)
# VBを実行する
model.execute(X, iter_max=100, thr=0.001)クラスタ数$K$は$8$として,他のパラメータは先ほどと同様の設定で行いました。

しっかりとクラスタリングできていますね。ログを確認すると,更新回数は$6$回だったことが分かります。
Log-likelihood gap: 12.22
Log-likelihood gap: 2.33
Log-likelihood gap: 1.33
Log-likelihood gap: 0.08
Log-likelihood gap: 0.01
Log-likelihood gap: 0.0
VB has stopped after 6 iteraions.EMアルゴリズムのときとは異なり,クラスタ数が過剰に設定されている場合でも変分ベイズでは正しくクラスタリングが行われていることが分かりました。このように,変分ベイズがスパースなクラスタ分類を行うはたらきを「関連度自動決定」と呼びます。クラスタの個数を大きめ($K=8$など)に設定すれば,勝手に適切なクラスタ数にフィットしてくれるというのです。
周辺尤度最大化するときにデータの傾向にそぐわない基底関数は周辺尤度を減少させる方向に寄与するため,勝手にクラスタ数をフィットしてくれるという訳です。詳しくは[1]の7.2.2章をご覧ください。
おわりに
本稿では,変分ベイズの目的とその実現方法を,点推定との比較を通じてボトムアップ的にお伝えしてきました。冒頭でも述べたように,変分ベイズは機械学習を学ぶ上で高く反り立つ壁です。多くの人が挫折を経験したことは想像に難くありません。本稿が,一人でも多くの人にとって変分ベイズを学ぶ助けとなれることを心から願っております。
[1] Christopher M. Bishop, "Pattern Recognition and Machine Learning."
付録
本章では,EMアルゴリズムと変分ベイズのEステップとMステップの対応を考えます。
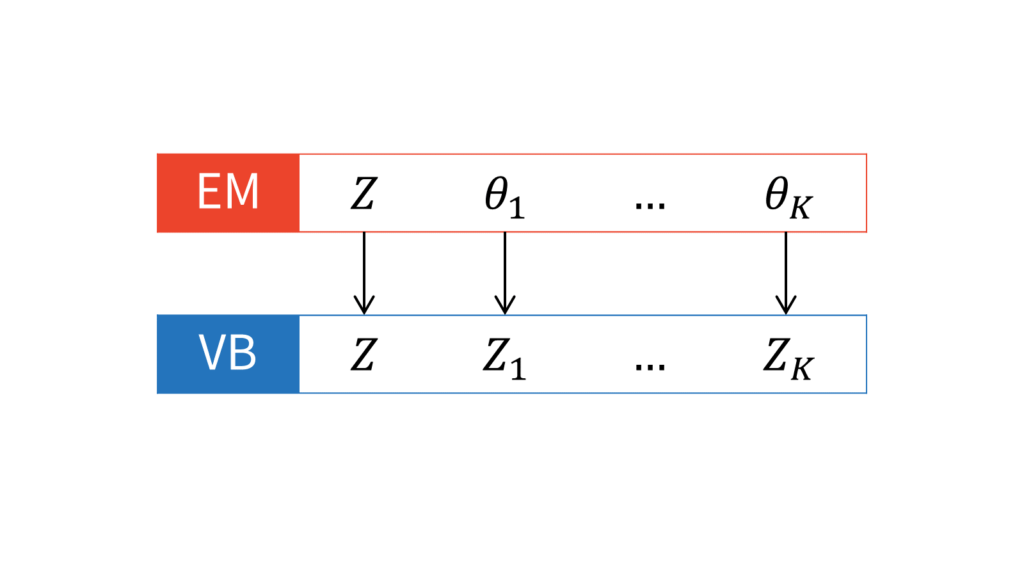
$Z$を構成する確率変数を$Z_0,\ldots,Z_K$と表すことにします。EMアルゴリズムでは潜在変数とパラメータは区別して,変分ベイズでは潜在変数にパラメータを含めるのでした。したがって,$Z_0,\ldots,Z_K$の中に,EMアルゴリズムにおける$\theta$が対応していることに注意してください。本稿では,潜在変数とそれ以外を明示的に区別するため,$Z_0$を潜在変数,それ以外の$Z_1,\ldots,Z_K$をパラメータと設定することにします。
変分ベイズは,言ってしまえば式($\ref{eq_vb_update}$)を計算するだけです。式(\ref{eq_vb_update})に基づけば,ある$Z_k$に対する更新を行うときは,$Z_k$以外の値を固定します。そのため,変分ベイズはEMアルゴリズムのような交互更新を行う必要があります。$K+1$個の$Z$に対して交互更新を行うため,理論上は$K+1$ステップ必要になります。
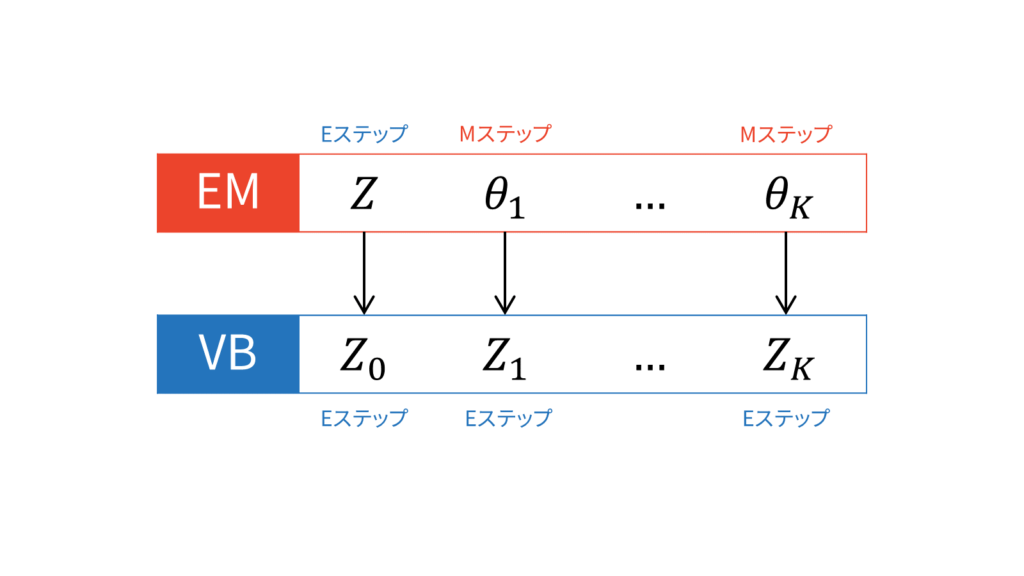
EMアルゴリズムと変分ベイズを比較する文脈では,変分Eステップと変分Mステップという用語が登場します。例えば,変分ベイズを混合ガウス分布に適用する場合,一般的には負担率を計算する変分Eステップとパラメータを更新する変分Mステップに分けられます。
変分ベイズにおいては,Mステップは存在しないというのが私の考えです。EMアルゴリズムにおけるMステップは,対数尤度を最大化するパラメータを点推定するステップでしたが,変分ベイズではパラメータを点推定するフェーズは存在しないからです。
多くの書籍やWeb上の資料では変分Eステップ・変分Mステップという用語が利用されているため,本稿では変分ベイズとEMアルゴリズムを対応付けたいと思います。いま,$K$種類のパラメータ$\vtheta$と潜在変数$Z$が存在するとします。すると,EMアルゴリズムは,$K$種類のパラメータを固定して潜在変数$Z$に関する最適化を行うEステップと,潜在変数$Z$を固定して$K$種類のパラメータを点推定するMステップで構成されます。このような立場に立つと,EMアルゴリズムはEM...Mアルゴリズムと捉えることができます(Mは$K$回連続しています)。
同じ立場に立てば,変分ベイズは$k+1$種類の確率変数$Z$がある状況ではEE...Eアルゴリズムと捉えることができます(Eは$K+1$回連続しています)。なぜなら,変分ベイズが式(\ref{eq_vb_update})を計算するだけだからです。EMアルゴリズムにおける$K$回のMステップが,全てEステップに置き換えられていますね。言ってしまえば,自分以外の期待値を取る操作を収束するまで繰り返すのが変分ベイズです。
特に「EM」アルゴリズムと比較する場合は,潜在変数$Z$とそれ以外のパラメータ$\theta$を別々に考えて,潜在変数以外の確率変数に関する式(\ref{eq_vb_update})を計算して$Z$に関するKLを最小化する$E_Z$ステップと,$\theta$以外の確率変数に関する式(\ref{eq_vb_update})を計算して$\theta$に関するKLを最小化する$E_{\theta}$ステップに無理矢理二分割します。
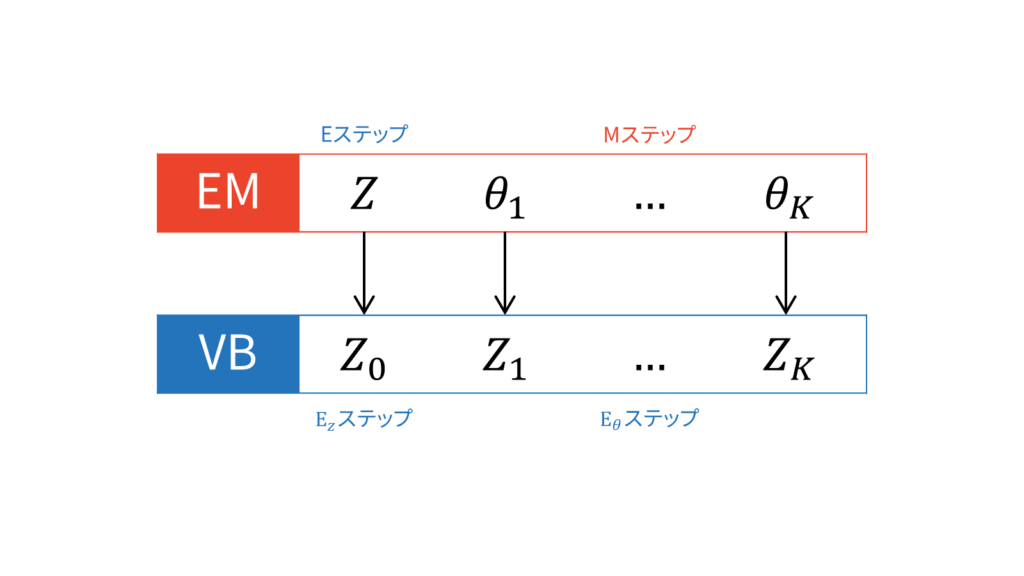
この$E_Z$ステップが巷では変分Eステップと呼ばれており,$E_{\theta}$ステップが変分Mステップと呼ばれているようです。しかし,私はこの呼び方が変分ベイズに対して誤解を生んでいる気がしてなりません。EMアルゴリズムとは違って,変分Mステップでは上限を最大化している訳ではないからです。あくまでも,両手法のMステップにおいては,潜在変数以外の確率変数(EMアルゴリズムで言えばパラメータという値)を最適化しているという対応関係しかありません。
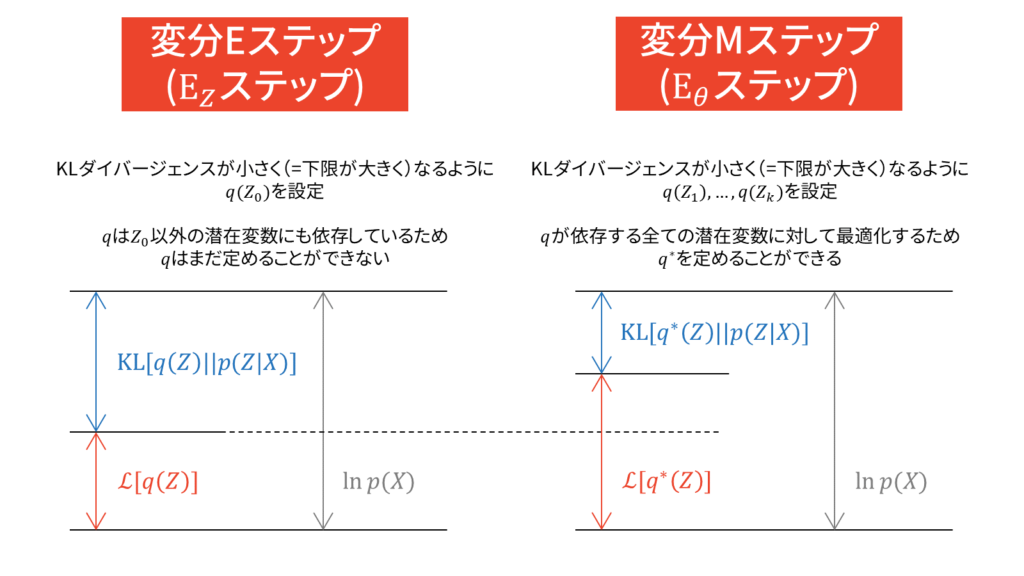
上図においては,先ほど設定したように$Z_0$は潜在変数を表しています。$Z_0$以外のパラメータは,先ほど説明した平均場近似の仮定をおくことで分離されているものとしています。変分Eステップでは,潜在変数$Z_0$に関して最適なパラメータ(負担率と呼ぶ)を求めておきます。
この時点では,実際に$Z_0$にとって最適なパラメータを探しただけであって,実際に更新はしていません。$Z_0$は他のパラメータとは異なり潜在変数です。パラメータの更新を行うのは変分Mステップであり,$Z_0$以外の因子についての最適化を行うことで変分下限を最大化します。このとき,変分Eステップで求めておいた負担率を利用することになるため,EMアルゴリズムと同様の交互更新になります。
しかし,本質的には変分ベイズでは潜在変数もパラメータも確率変数とみなしていますので,潜在変数とパラメータの立場は対等なはずです。変部ベイズにおいて「潜在変数とそれ以外」を区別する必要性が,私はあまりないように感じています。逆に言えば,両者を同一視した概念が変分ベイズだと思っています。
多くの書籍やWeb上の資料では,負担率という言葉だけが一人歩きしているように思えます。負担率の本質はEステップで計算される値であり,Mステップのパラメータ更新で利用される値であるということです。


コメント
コメント一覧 (41件)
初めまして。高橋と申します。zuka様のWebサイトはPRMLの演習問題を解くときに大変お世話になりました。
現在変分法を勉強しているとこだったのでとても勉強になっております。
1点ご質問なのですが、対数尤度と下限の差を取りKLダイバージェンスを導出するとこの式変形についてです。書き忘れ、消し忘れだとは思うのですが、
(21)から(22)にかけてlogP(X|Θ)は相殺されて消えると思うのですがいかがでしょうか。また(22)の式全体の符号はマイナスだとおもいました。
突然の連絡大変失礼いたしました。これからも応援しております!
高橋様
ご連絡誠にありがとうございます!
ご丁寧にご指摘いただき本当に助かります。
本文を修正致しました。
前のサイトからの読者様ということで,非常に嬉しく思います。
これからも分かりやすく正確な発信を心掛けていますので,何卒よろしくお願い致します!
素晴らしい記事をありがとうございます!
EMアルゴリズム、変分ベイズ、transformerとよくわからない概念が出てくるたびにzuka様のサイトがとても参考になるので本当に感謝しています。
ささいな点ですが、式番号(49)から(50)のところで符号が反転しているので、(50)から(57)のarg minはarg maxの事なのではないかと思いました。
田中様
ご指摘誠にありがとうございます!
非常に助かります。
式(49)-式(57)にかけて,$\arg \min$を$\arg \max$に修正しました。
いつも記事をご覧いただき嬉しい限りです。
他にも疑問点や分かりにくい箇所等ございましたら,お気軽にお申し付けください!
非常に細かいですが、「平均近似場」ではなく「平均場近似」ではないでしょうか?
mogmog 様
ご指摘ありがとうございます!
お恥ずかしい限りです。修正致しました。
はじめまして
詳しい説明ありがとうございます。
PRMLの演習解説はブックマークさせてもらっています。
質問なんですが、式(31)~(32)でのInCとCの意味が理解できていません。
定数だろうとは思うのですが、ここで引いたり分母を割っているのが...
まだまだ、勉強不足です。
教えていただけるとうれしいです。
sumeragi さま
ご質問ありがとうございます。前のブログからの読者さまということで,非常に嬉しく思います。
さて,式(31)~(32)でのInCとCの意味に関してですが,非常によい質問だと思います。本文中で定数を足し引きしたのは,式(15)の形を出現させるためです。式(15)は平均場近似を用いた変分推論の解として知られていますから,いわば天下り的に定数を足し引きしていると解釈してもらえればと思います。
それでは,この定数が何を意味しているのかというと,分布の正規化定数を表しています。これはGMMへの適用が理解の助けになるでしょう。式(108)は式(15)におけるconstを無視して求められる解ですが,このままでは確率変数に関する総和が$1$とならず,$q^{\ast}$が確率分布の定義を満たしません。そこで,一旦式(15)におけるconstを無視して求められる解を計算してしまい,正規化定数は別途求めるというアプローチを取ります。このとき求められた正規化定数が,式(15)におけるconstに相当します。
以上から,式(31)~(32)で定数を足し引きしているのは,正規化定数までをも含んだ形で変分推論の解を示すためだといえます。
いつもお世話になっております。大変分かりやすい記事ありがとうございます。
さて、細かい話にはなるのですが、式(133)に関して、右辺第一項の、pi_kの乗数ですが、alpha_0ではなく、alpha_0kではないでしょうか?つまり、alpha_0はベクトルですので、その第k成分を乗ずるのではないでしょうか?
これに伴って、式(134)、(135)も、シグマの外ではなく中にalpha_0が入ってくるものと思います。
同様に式(135)のN_kに関しても、kのシグマの中に入れるべきではないでしょうか?
これらが正しければ、式(138)から(141)までも少し修正すべきだと思われます。
もし間違っていたら申し訳ありませんが、確認していただけますでしょうか?
Bayes様
ご質問誠にありがとうございます。
>式(133)に関して、右辺第一項の、pi_kの乗数ですが、alpha_0ではなく、alpha_0kではないでしょうか?
仮定の記述が抜けておりました。$K$クラスの初期値の対称性より,$\valpha_{0}$の全ての要素を$\alpha_{0}$としました。
>同様に式(135)のN_kに関しても、kのシグマの中に入れるべきではないでしょうか?
おっしゃる通りです。ディリクレ分布の恒等式まわりの記述に関して,全面的に修正致しました。
以上,お手隙の際にご確認いただけますでしょうか。ご指摘非常に助かります!
大変分かりやすい記事ありがとうございます.
一点だけ教えていただけないでしょうか?
(104)式では尤度の部分に対数は現れないのでしょうか?
また(107)ではz_nkがlogρにかけられているのに対して,(105)式ではlogπのみにかけられているのも気になります.
確認いただけますでしょうか?
EMアルゴリズムから読ませていただいていて,大変勉強になっております.ありがとうございます。
はり様
ご質問と温かいお言葉ありがとうございます。
>(104)式では尤度の部分に対数は現れないのでしょうか?
すみません,誤植です。修正致しました。
>(107)ではz_nkがlogρにかけられているのに対して,(105)式ではlogπのみにかけられているのも気になります.
恐れ入りますが,式番号がズレてしまったかもしれません。お手数ですが,今一度質問をご確認いただけますでしょうか。
式103について質問です。
式36などの変分ベイズの更新式を見ると、qi≠jに対する期待値が取れられていますが、式103では、qi≠jに対する期待値が取られていないように見えます。
こちらはどのようなことが意味されているのでしょうか?
「平均場近似のグループ分け」にて、$\mZ$と$\vpi, \vmu, \mSigma$がそれぞれ別のグループに属すると仮定しています。変分ベイズの更新式では「自分以外全ての潜在変数・パラメータで仮定した確率モデルの期待値を取ると近似事後分布の形が得られ」ますので,$\mZ$の近似事後分布を求めるためには$\vpi, \vmu, \mSigma$に関する期待値を考えればよい,となります。
度々申し訳ありません。
式(103)-(104)の式変形について質問です。
式(67)では、p(X,Z,π,μ,Σ)=p(X|Z,μ,Σ)p(Z|π)p(π)p(μ|Σ)p(Σ)となっています。
しかし、式(103)-(104)のp(X,Z,π,μ,Σ)の式変形の際に、p(Z|π)、p(X|Z,μ,Σ)以外はなぜ、消えてしまっているのでしょうか?
$\vpi, \vmu, \mSigma$に関する期待値を考えているからです。例えば,$X$に関する期待値$E[X]$は定数になりますよね。それと同じで,$\vpi$に関する$p(\vpi)$の期待値,$\vmu$に関する$p(\vmu|\mSigma)$の期待値,$\mSigma$に関する$p(\mSigma)$の期待値は定数になります。なお,期待値の線形性は自明としています。
上記2点、理解することができました。
ご回答いただき、ありがとうございます。
追加で質問させていただきたいのですが、定数1/Aを、式(109)のように定めている理由としては、「rnkを式(119)のような形で表したいから」、でしょうか?
Yu様
ご質問ありがとうございます。
>定数1/Aを、式(109)のように定めている理由としては、「rnkを式(119)のような形で表したいから」、でしょうか?
いえ。確率の定義から$q^{\ast}(\mZ)$の$\mZ$に関する総和は$1$となることを利用しています。すなわち,下記関係式を利用しています。
\begin{align}
\sum_{\mZ}q^{\ast}(\mZ) &= A\sum_{\mZ} \prod_{n=1}^{N} \prod_{k=1}^{K} \rho_{nk}^{z_{nk}} = 1
\end{align}
ご回答ありがとうございます。
理解できました、、、
何度も何度も申し訳ありません、、、
式(121)の右辺の第四項の式変形の理解に苦戦しております。
この式変形を理解するために、どのような情報を参照したらよろしいでしょうか?
Yu様
ご質問ありがとうございます。
>この式変形を理解するために、どのような情報を参照したらよろしいでしょうか?
すみません,本文に誤植がありましたので修正致しました。併せて導出も含めて補足も書いてみました。
追記、及び修正ありがとうございます。
現在、(121)の証明を行おうとしておりますが、(3)のようになってしまうため、何点かお伺いしたいことがあります、、、
1. a~N(m, Σ)の認識でよろしいでしょうか、、、?
2. Aはどのような行列でしょうか、、、?
3. 以下の式(3)のように、(121)式の右辺第二項のTr(AΣ)のようにすっきりした式になりませんでした、、、どのようにすればTr(AΣ)が導出できるのでしょうか、、、?
お手数ですが、ご回答いただけますと幸いです。
よろしくお願いいたします。
=== (121)の証明 ===
E[(x-a)T A (x-a)] を以下のように、変形しております。
※EはEa,Aのことです、、、
E[(x-a)T A (x-a)] = E[xT A x - aT A x - xT A a + aT A a + xT x + aT a]
= xT E[A] x - E[aT] E[A] x - xT E[A] E[a]+ E[aT A a] + xTx + E[aT a]
ここで、a~N(m, Σ)だとすると、
= xT E[A] x - mT E[A] x - xT E[A] m + xTx + mT m + E[aT A a]
= (x-m)T E[A] (x-m) + E[aT A a] (1)
E[aT A a]について、aT A a = Tr(aT A a)=Tr(A a aT)となるから、
E[aT A a] = E[Tr(A a aT)] = Tr(E[A a aT])
ここで、Aは定数行列?なら、E[aT A a] =Tr(A E[a aT]) (2)
aの共分散行列がΣの場合、
Σ=E[(a-m)(a-m)T]
=E[a aT - a mT - m aT + mmT]
よって、E[a aT] = Σ - E[- a mT - m aT + mmT]
= Σ + E[a mT + m aT - mmT]
これを、(2)に代入すると、E[aT A a] = Tr{A (Σ + E[a mT + m aT - mmT])}
これを、 (1)に代入すると、
E[(x-a)T A (x-a)] = (x-m)T E[A] (x-m) + Tr{A (Σ + E[a mT + m aT - mmT])} (3)
Yu様
ご質問ありがとうございます。すみません,誤植がありました。丁寧めに解説を追記してみましたので,ご確認お願い致します。
念の為ご質問にお答えします。
>1. a~N(m, Σ)の認識でよろしいでしょうか、、、?
こちらノーテーションを再定義致しました。
>2. Aはどのような行列でしょうか、、、?
こちらもノーテーションを再定義致しました。
>3. 以下の式(3)のように、(121)式の右辺第二項の...
こちらも再度本文をご確認いただけますでしょうか。
ご丁寧に解説いただき、ありがとうございます、、、
式(128)-(129)において、Eμ[μμT]が、mmT+(βΣ)^-1になっているのですが、なぜ、(βΣ)^-1も現れるのでしょうか、、、?
ご質問ありがとうございます。お手数ですが、直後にある式(141)以降の説明をご覧いただけますでしょうか。
再び失礼します。
このサイトでは分散共分散行列を精度行列として定めてると思いますが、実装の部分でgmm_pdfでは多変量正規分布の引数のcovが精度行列のまま入力してます。これはどういう意図なんでしょうか?
はり様
ご質問ありがとうございます。
>実装の部分でgmm_pdfでは多変量正規分布の引数のcovが精度行列のまま入力してます。
いえ、分散共分散行列として入力しております。実際、m_stepにおいて更新式よりW_invを計算し、その逆行列をself.Wに代入しております。ご確認お願い致します。
zuka様
返信ありがとうございます.
大変恐縮ではございますが,私の認識がどこからずれてしまっているか一つ一つ確認して教えていただけないでしょうか?お手数おかけして,申し訳ございません.
1. self.Wはウィシャート分布のパラメータである.
こちらは実装部分のm_stepの説明のところに明記されてあるかと思います..
2. 分散共分散行列の逆行列に関するガウス分布の共役事前分布はウィシャート分布である.
こちらは"1. 同時分布の依存関係確認"の箇所に記述があると思います.
3. ウィシャート分布の期待値(self.nu*self.W)は精度行列が従う分布の期待値である.
1. と2. から読み取りました.
zuka様,重ね重ね申し訳ありませんがよろしくお願い致します.
はり様
大変失礼しました。ご指摘の通りです。的確かつ丁寧なご指摘ありがとうございます。ソースコードを修正致しました。こちらで認識合いますでしょうか。なお、ついでにdockerを用いてVBを実行できるように改修しました。お手隙にご確認お願い致します。
https://github.com/beginaid/GMM-EM-VB
式55-56の式変形で, 式56のln(p(z)/q(z))はln(q(z)/p(z))ではないでしょうか
よしお様
ご質問ありがとうございます。EMアルゴリズムの下限導出を参考にすると、$q$の下限は$q\ln p/q$になると思っていますが、自分の理解が不適切であればご指摘ください。
非常に詳細かつ緻密な解説をいただき、感謝いたします。その上で質問です。ただし、VBにおける潜在変数とEMにおける潜在変数を$Z^{\VB}$と$Z^{\EM}$と区別させていただきます。
平均場近似は、$q(Z^{\VB})$は独立な分布$q_{i}(Z_{i})$の積で表されるという仮定だと認識しております。このノーテーションをもとに考えれば、GMMでは潜在変数を$Z_{1}{=}\{Z^{\EM}\}$,$Z_{2}{=}\{\pi,\mu,\Sigma\}$と分割しておられるのだと思います。しかし、$p(Z^{\EM})$が定義されず、代わりに$p(Z^{\EM}|\pi)$が定義されていることからも、$Z^{\EM}$と$\pi$は独立しているとは言えないように感じます。なぜ$Z_{1}{=}\{Z^{\EM},\pi\}$,$Z_{2}{=}\{\mu,\Sigma\}$としないのでしょうか?
うさぎさま
ご質問ありがとうございます。
>平均場近似は、$q(Z^{\VB})$は独立な分布$q_{i}(Z_{i})$の積で表されるという仮定だと認識しております。
はい。自分の理解と合います。
>GMMでは潜在変数を$Z_{1}{=}\{Z^{\EM}\}$,$Z_{2}{=}\{\pi,\mu,\Sigma\}$と分割しておられる
こちらは自分の理解と合いません。
お手数ですが、記事最下部の「付録」をご確認いただけますでしょうか。
付録をご覧いただいた上でご質問がある場合は、再度コメントいただけますと幸いです。
ご返信ありがとうございます。
> 記事最下部の「付録」をご確認いただけますでしょうか
「付録」でおっしゃっていることを要約すると、
- VBにおける潜在変数$Z$は、EMにおける潜在変数を$Z_0$として、またモデルパラメタ$\theta_1, \theta_2, \cdots, \theta_K$を$Z_1, Z_2, \cdots, Z_K$として含んでいる
- VBにおける最適化は$Z$の要素を平均場近似によって排反かつ独立なグループに分割し、各グループにおいて他のグループの値を固定した時の期待値を計算し続ける
のように書けると思いますが、まず認識として齟齬がありますでしょうか。その上で、式(16)と式(90)の比較から、GMMではこのグループについて$Z_0 = Z^{\text{EM}}, Z_1 = \{\boldsymbol{\pi}, \boldsymbol{\mu}, \boldsymbol{\Sigma} \}$のような対応関係にある(より正確には、$Z_0 = Z^{\text{EM}}, Z_1 = \boldsymbol{\pi}, Z_2 = \{ \boldsymbol{\mu}, \boldsymbol{\Sigma} \}$)のだと解釈しております。
分割がどうであったとしても、潜在変数と他のパラメータ(特に$\boldsymbol{\pi}$)が独立であるという仮定を置きながら、$p(\boldsymbol{Z})$の分布を陽に置かず、$\boldsymbol{\pi}$に依存した分布、すなわち$p(\boldsymbol{Z} | \boldsymbol{\pi})$しか定義しない、また計算においてもそれしか用いないことが腑に落ちていません。仮にこの2変数が独立であるならば、$p(\boldsymbol{Z}) = p(\boldsymbol{Z} | \boldsymbol{\pi})$が成立し、分布を$\boldsymbol{Z}$のみで表現することが可能ではありませんか?
理解が足りず大変申し訳ございませんが、何卒ご教授をお願いいたします。
うさぎさま
なるほど。理解しました。
>潜在変数と他のパラメータ(特に$\boldsymbol{\pi}$)が独立である
こちらが自分の理解と合っておりません。
式(90)の直後にその理由を記載してみました。
私が勘違いしている可能性もございますので,もし疑問が残る場合は再度ご指摘いただけますでしょうか。
いつも記事読ませていただいております。
(105),(107)式の4項目の係数は「-1/2」だと思います。
maruさま
ご指摘ありがとうございます。おっしゃる通りですので本文を修正しました。
ある目的があって変分ベイズを勉強し始めたところ、このサイトにたどり着きました。難しい内容ですが、この方法の理解に大変役に立っています。
以下、いくつか質問です。
・(56)の第二項の分数部分はKLダイバージェンスの定義により、q(Z)/p(Z) ではないでしょうか。
・(176)、(177)は (175)と同様に、∑(k=1,..,K) の総和の形ではないでしょうか。
・(187)の最終行の二つの項の符号は(186)より+になるのではないでしょうか。
・(189)の左辺の分子はNk + ν0 - D – 1ではないでしょうか。
・(190)の下からの文章ですが、項~に注目して、項~に関する恒等式、などはWに関するではなく∑k に関するものと思いますがいかがでしょうか。
・(201)は(200)と同じく∑(n=1,..,N)の総和の形ではないでしょうか。
bluestat 様
ご返信遅れまして大変失礼しました。
>式(56)について
対数の差への分解が誤っておりました。
>式(176)〜式(177)について
ご指摘の通り,総和が抜けておりました。
>式(187)について
ご指摘の通り,符号が誤っておりました。
>式(189)について
式(85)のウィシャート分布の定義を利用しております。
>式(190)について
ご指摘の通り,$\mSigma_{k}$に関する整理でした。
>式(201)について
ご指摘の通り,総和が抜けておりました。
以上,修正が完了しました。ご指摘非常に助かりました。
式(57)は、∫q(z)lnp(x)dz - KL[q(z)|p(z|x)] としてもよいですか?
ご質問ありがとうございます。
はい、ご提示いただいた表現でも問題ありません。
\begin{align}
\calL_{\VB} \left[ q(Z) \right]
&= \int_{Z} q(Z) \left[\ln p(X,Z) - \ln q(Z)\right]dZ \\[0.7em]
&= \int_{Z} q(Z) \left[\ln \{p(Z|X)p(X)\} - \ln q(Z)\right]dZ \\[0.7em]
&= \int_{Z} q(Z) \left[\ln p(Z|X) + \ln p(X) - \ln q(Z)\right]dZ \\[0.7em]
&= \ln p(X)\int_{Z} q(Z) dZ + \int_{Z}q(Z)\left[\ln p(Z|X) - \ln q(Z)\right]dZ \\[0.7em]
&= \ln p(X) - \int_{Z}q(Z)\left[\ln \frac{q(Z)}{p(Z|X)}\right]dZ \\[0.7em]
&= \ln p(X) - \KL\left[q(Z)|p(Z|X)\right]
\end{align}
のように計算できます。