本記事は機械学習の徹底解説シリーズに含まれます。
初学者の分かりやすさを優先するため,多少正確でない表現が混在することがあります。もし致命的な間違いがあればご指摘いただけると助かります。
はじめに
近年の深層学習ブームにおいて,VAE(変分オートエンコーダ: variational autoencoder)の果たした貢献は非常に大きいです。GAN(敵対的生成ネットワーク: generative adversarial network)やFlowと並んで,生成モデルの三大巨頭として主に教師なし学習や半教師あり学習で応用されています。
多くの書籍やWeb上の資料では「VAEはオートエンコーダの発展手法である」と説明されています。名前にもAE(オートエンコーダ)と入っているので,そう思ってしまうのは一見当然のことのように思えます。しかし,語弊を恐れずに言うと,この説明は深刻な誤解を読者に与えています。Kingmaらの原著論文を読めば,VAEがAEを元に出発しているのではなく,あくまでも変分推論の枠組みで考案された事後分布の近似手法であることが分かります。
本稿は,読者の皆さまにVAEを正確に理解していただくため,VAEがEMアルゴリズムと変分ベイズ(VB: variational Bayes)を融合させた手法であることをお伝えしていきます。決して,オートエンコーダの発展手法ではないということを肝に銘じてください。
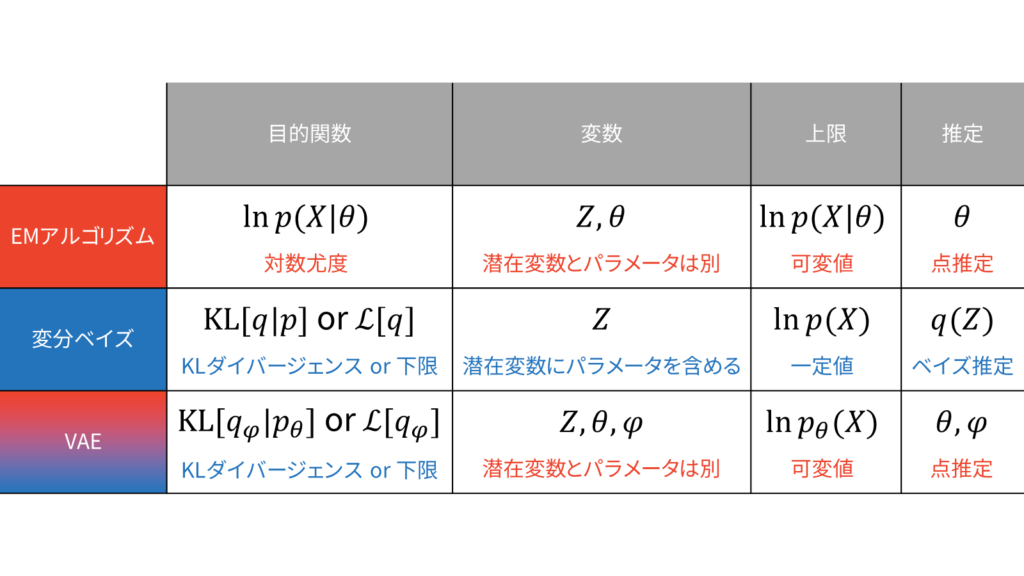
上図を理解していただくため,本稿では以下の流れで説明を行います。
VAEがどのような枠組みで何のために用いられるのかを説明します。
点推定とベイズ推定を実現するための枠組みについて説明します。
変分ベイズの枠組みでVAEを説明します。
MNISTを題材にしてVAEの定式化を確認します。
MNISTを題材にしてVAEの実装方法を確認します。
VAE・GAN・Flowの様々な流派を紹介します。
VAEの目的
VAEは事後分布を近似するための手法です。結果としてオートエンコーダ型になっているだけで,オートエンコーダの応用手法として発表された訳ではありません。VAEは,KingmaらのAuto-Encoding Variational Bayesという論文で発表されました。論文タイトルを素直に直訳すると「オートエンコーダ型変分ベイズ」となります。このタイトルからも推測される通り,VAEでは変分ベイズのアイディアを一部用います。
一般的な変分ベイズでは,近似事後分布に平均場近似の仮定を置いていたため,近似事後分布の表現力に限界がありました。そこで,Kingmaらは近似事後分布にDNN(深層ニューラルネットワーク)を導入しました。さらに,誤差逆伝播に基づくDNNの学習を可能にするため,潜在変数を決定的に抽出することで微分可能な定式化(Reparameterization trick)も行いました。
そこで,以下では最初に変分ベイズについて復習したうえで,VAEに立ち戻るという方針を採用します。さらに,変分ベイズを正確に理解するためには最尤推定やMAP推定の理解が必須になるため,EMアルゴリズムの概要も併せて確認するようにしましょう。
EMアルゴリズムと変分ベイズ
本章では,EMアルゴリズムと変分ベイズがどのような目的で用いられるのかを説明します。先に結論からお伝えすると,EMアルゴリズムは潜在変数を含む確率モデルの点推定を行うため,変分ベイズは潜在変数を含む確率モデルのベイズ推定を行うための手法です。そこで,まずは確率モデルと点推定・ベイズ推定について解説していきます。
確率モデル
確率モデルというのは「現象の裏側に何か適当な分布を仮定する」枠組みのことです。私たちの目的は,ある現象を確率分布を用いて記述することです。そのためには,以下のステップが必要になります。
- ある現象をよく観察して最もよくフィットする既存の確率分布を選択する
- 仮定した確率分布の形状を決定するパラメータを推定する
ある現象に対して既存の分布を仮定するという操作は,観測データの発生方法に対して尤度関数(ベイズ推定の場合は同時分布)を定めることに相当します。すると,私たちの最終的な目的は,分布の形状を決定するパラメータを推定することになります。
パラメータの推定方法は,パラメータを1つの値に決め切ってしまう点推定と,パラメータ自体にも既存の分布を仮定するベイズ推定に分けられます。さらに,点推定は尤度関数を最大にする最尤推定と事後確率を最大にする最大事後確率(MAP: maximum a posteriori)推定に分けられます。
- 点推定
- 最尤推定
- MAP推定
- ベイズ推定
以下では,数式を用いて点推定とベイズ推定を説明していきます。
点推定
あるパラメータ$\theta$が与えられたときに,観測データ$X$のふるまいを定義する関数$p(X|\theta)$が尤度関数です。最尤推定では,尤度関数$p(X|\theta)$を最大にする$\theta$の値を求めます。
\hat{\theta}_{\ML} &= \argmaxTheta p(X | \theta)
\end{align}
条件付き確率の定義より,$p(X | \theta)$は「$\theta$が与えられたときの$X$」の確率を表します。言い換えれば「$\theta$が与えられたときに$X$はどれだけ尤もらしいか」を表しています。最尤推定では,条件付けられた$\theta$を変数として読み替えることで,データ$X$に対して最も尤もらしいパラメータ$\theta$を推定します。
一方で,MAP推定では事後確率$p(\theta|X)$を最大にする$\theta$の値を求めます。
\hat{\theta}_{\MAP} &= \argmaxTheta p(\theta | X) \\[0.7em]
&= \argmaxTheta \frac{p(X | \theta)p(\theta)}{p(X)} \\[0.7em]
&= \argmaxTheta p(X | \theta) p(\theta)
\end{align}
ただし,変形にはベイズの定理を利用しました。$\theta$に関する最大化問題であるため,最終行では$p(X)$を無視しました。
ベイズ推定
ベイズ推定では,パラメータを値ではなく分布として求めることで,データへの過学習を防止したり,表現力を上げたりすることができます。パラメータの分布というのは,ある観測データ$X$が得られたときの事後分布$p(\theta | X)$のことを表しています。
p(\theta | X) &= \frac{p(X | \theta)p(\theta)}{p(X)}
\end{align}
点推定とは異なり,ベイズ推定では$\arg \max$が付いていませんね。$\arg \max$・$\arg \min$は目的関数が最大・最小になるパラメータを値として求めることを意味しています。耳が痛いようですが,ベイズ推定では仮定した確率分布$p$の形状を決めるパラメータ$\theta$の事後分布$p(\theta | X)$を求めます。
各種推定方法の実現
本章では,各種パラメータの推定方法がどのように実現されるのかについて説明します。先に結論からお伝えすると,点推定を実現する方法はEMアルゴリズム,ベイズ推定を実現する方法は変分ベイズがよく利用されます。
- 点推定
- EMアルゴリズム
- ベイズ推定
- 変分ベイズ(変分推論)
確率モデルの問題を考えるときには,最初に確率モデルに潜在変数$Z$(尤度関数に姿を現さない変数)を導入します。そうすることで,複雑な分布をより単純な分布を使って表すことが可能になります。潜在変数を導入することは,同時分布$p(X,Z)$を設計することに相当します。ここが全ての始まりです。観測データ$X$と潜在変数$Z$にどのような依存関係があるのかを同時分布として設定してしまうわけです。
ベイズ推定では,副次的に尤度関数$p(X|Z)$と事前分布$p(Z)$を仮定することになります。
変分ベイズを含む従来のベイズ推定の手法では,計算が煩雑になるという欠点があります。一方で,VAEでは近似分布のみならず,真の分布もDNNによって推定しますので,確率的勾配法を用いて一気通貫にパラメータを最適化することができます。
EMアルゴリズム
EMアルゴリズムの目的は,潜在変数を含む確率モデルの点推定を行うことでした。EMアルゴリズムでは,潜在変数を$Z$とパラメータ$\theta$を区別します。また,EMアルゴリズムでは$p(Z|X)$を計算できるという立場を取ります。
さらに,EMアルゴリズムにおけるEステップとMステップは以下のように説明することができます。

EMアルゴリズムに関する詳しい解説は「EMアルゴリズムをはじめからていねいに」をご参照下さい。
変分ベイズ
変分ベイズの目的は,確率モデルの潜在変数・パラメータに関する事後分布を求めることでした。EMアルゴリズムでは潜在変数を$Z$,パラメータを$\theta$と区別しましたが,変分ベイズでは両者を一括りにして$Z$と表しますので,事後分布は$p(Z|X)$と表されます。EMアルゴリズムでは$p(Z|X)$を計算できるという立場を取りましたが,変分ベイズでは$p(Z|X)$を計算できないという立場を取ります。
変分ベイズは,事後分布$p(Z|X)$を別の新しい分布$q(Z)$で近似してしまおうという大胆かつ汎用性の高い手法です。
q(Z) &\sim p(Z|X)
\end{align}
結論からお伝えすると,EMアルゴリズムと変分ベイズは以下のような違いがあります。
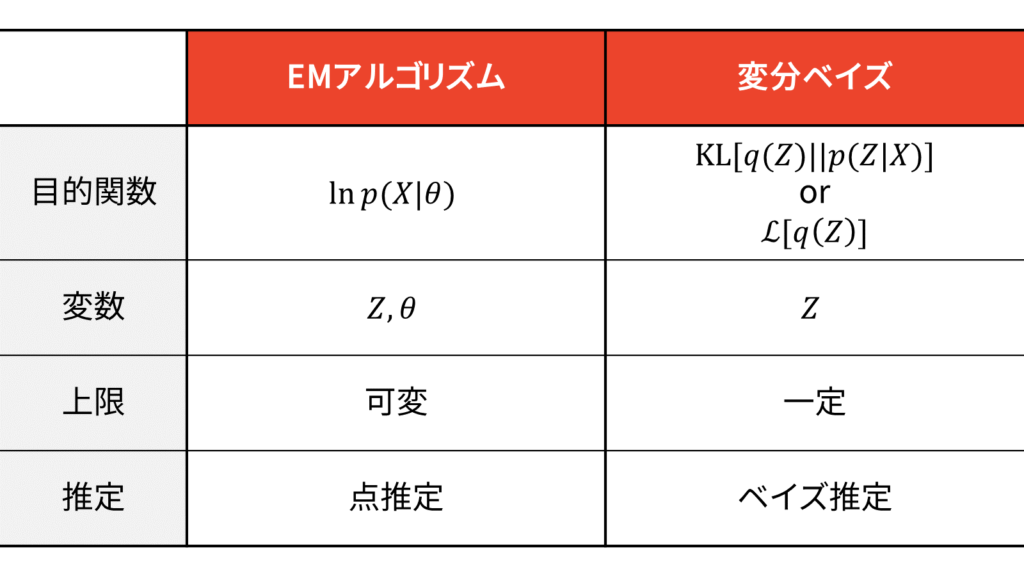
さらに,変分ベイズにおけるEステップとMステップは以下のように説明することができます。
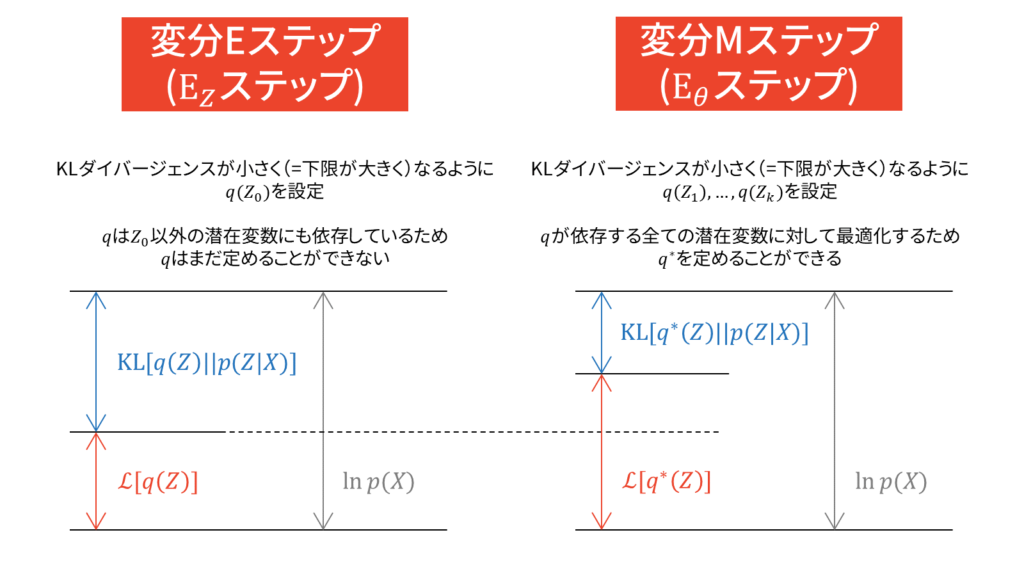
変分ベイズに関する詳しい解説は「変分ベイズをはじめからていねいに」をご参照下さい。
VAEの成り立ち
変分ベイズの着眼点は,事後分布の計算が難しいという問題でした。Kingmaらも同様に,一般的な確率モデルの問題設定に対して,以下のような問題を挙げています。
- Intractability:事後分布$p(Z|X)$の計算が困難
- A large dataset:データセットが巨大なため計算量の多い手法は使いにくい
ここで,事後分布は計算が難しいことの一般的な説明をしておきます。ベイズの定理を用いると,事後分布を以下のように表すことができるのでした。
p(Z | X) &= \frac{p(X | Z)p(Z)}{p(X)} \\[0.7em]
&= \frac{p(X | Z)p(Z)}{\int p(X, Z)dZ}
\end{align}
このとき,分母に出てきた周辺尤度に積分が含まれており,計算が難しくなってしまうのです。他にも,分子の尤度関数と事前分布に関して共役事前分布を設定しない状況を考えると,事後分布(同時分布)を計算することが困難になってしまいます。Kingmaらは,この課題を「Intractability」と呼んでいます。
このような背景から,計算が難しい事後分布を近似しようという手法が歴史上数多く提案されています。これらの手法は大きく「サンプリング」と「変分ベイズ」に分けられます。一般に,サンプリングによる近似は計算量が多くなってしまいます。Kingmaらは,この課題を「A large dataset」と呼んでいます。一方で,変分ベイズは大規模な計算にも対応できるという利点があります。
そこで,VAEでは「変分ベイズ的に」事後分布を近似できるような近似分布$q(Z)$を持ち出して,真の事後分布を近似します。VAEでは変分ベイズとは異なり,平均場近似を仮定せずに近似事後分布を新しく持ち出した分布$q$の事後分布$q(Z|X)$としてDNNで学習させます。そうすることで,真の事後分布が複雑な形状をしている場合でも,近似事後分布で表現できるようになります。
変分ベイズの類推
数式で説明していきましょう。変分ベイズの下限最大化の文脈において,$q(Z)=q(Z|X)$と置き換えます。すなわち,VAEの文脈における分解式は以下のようになります。
\calL_{\VAE}[q_{\varphi}(Z|X)] &= E_{q_{\varphi}}\left[ \log p_{\theta}(X|Z) \right]-\left.\KL\left[ q_{\varphi}(Z|X) \right\| p(Z) \right] \label{eq_L_VAE}
\end{align}
この結果は,対数周辺尤度にイェンセンの不等式を利用して得られる以下の分解式からでも確認することができます。
\ln p(X) &= \calL_{\VAE}[q(Z|X)] + \left. \KL \left[q(Z|X) \right\| p(Z|X) \right]
\end{align}
上記分解式の導出は「EMアルゴリズムをはじめからていねいに」をご参照ください。さて,実際に計算してみましょう。
&\calL_{\VAE}[q_{\varphi}(Z|X)] \notag \\[0.7em]
&= \ln p_{\theta}(X)-\left.KL[q_{\varphi}(Z|X) \right\| p_{\theta}(Z|X)] \\[0.7em]
&= \ln p_{\theta}(X)-E_{q_{\varphi}}\left[ \log q_{\varphi}(Z|X)-\log p_{\theta}(Z|X) \right] \\[0.7em]
&= \ln p_{\theta}(X)-E_{q_{\varphi}}\left[ \log q_{\varphi}(Z|X)-\log \frac{p_{\theta}(X|Z)p(Z)}{p_{\theta}(X)} \right] \\[0.7em]
&= \ln p_{\theta}(X)-E_{q_{\varphi}}\left[ \log q_{\varphi}(Z|X)-\log p_{\theta}(X|Z)-\log p(Z)+\log p_{\theta}(X) \right] \\[0.7em]
&= E_{q_{\varphi}}\left[\ln p_{\theta}(X)-\log q_{\varphi}(Z|X)+\log p_{\theta}(X|Z)+\log p(Z)-\log p_{\theta}(X) \right] \\[0.7em]
&= E_{q_{\varphi}}\left[ \log p_{\theta}(X|Z) \right] - E_{q_{\varphi}} \left[ \log q_{\varphi}(Z|X)-\log p(Z) \right] \\[0.7em]
&= E_{q_{\varphi}}\left[ \log p_{\theta}(X|Z) \right]-\left.\KL\left[ q_{\varphi}(Z|X) \right\| p(Z) \right]
\end{align}
上記変形は,変分ベイズにおける下限最大化の文脈で計算した過程と全く同じです。
式($\ref{eq_L_VAE}$)の第一項目は対数尤度の近似事後分布に対する期待値,第二項目は近似事後分布と事前分布の負のKLダイバージェンスを表しています。特に,第一項目は「近似事後分布にしたがって得られた潜在変数から入力データがどれだけ尤もらしいか」を表す数値であり,本質的に再構成誤差と等価になります。
\text{下限} &= q\text{による対数尤度の期待値} + \text{近似分布と事前分布の負の距離} \\[0.7em]
&= \text{再構成誤差} + \text{正則化項}
\end{align}
例えば,尤度関数に正規分布を仮定した場合は,再構成誤差は二乗誤差に対応します。本稿では,尤度関数にベルヌーイ分布を仮定するケースを考えますので,再構成誤差はバイナリクロスエントロピーに対応します。
ちなみに,再構成誤差だけで近似事後分布を計算する手法が素朴なオートエンコーダです。多くのWeb上の資料や書籍などでは,変分推論の背景を完全に無視して「オートエンコーダ型の損失関数に事前分布による正則化項を付け加えた手法である」という説明がなされています。説明自体は間違えていないのですが,VAEが導入された文脈や背景などを誤解する恐れがありますので,十分に注意してください。
VAEでは,下限を最大化もしくはKLダイバージェンスを最小化します。このとき,DNNで近似事後分布$q(Z|X)$を学習するため,近似事後分布はDNNのパラメータ$\varphi$に依存することになります。DNN界隈では,分布$q$がパラメータ$\varphi$に依存することを$q_{\varphi}$と書くことが多いため,本記事でもそれに倣うことにします。すなわち,VAEにおける近似事後分布は$q_{\varphi}(Z|X)$ということになります。
KLダイバージェンスは非対称ですので,$\KL(p\|q)$と$\KL(q\|p)$は異なります。機械学習の文脈では,前者をForward KL,後者をReverse KLと呼ぶことがあります。KLダイバージェンスの定義より,Forward KLは$\log$関数を$p$で重みづけしていますので,$p \neq 0$の部分を$q$で網羅しようとします。その結果,$q$の分散は大きくなりやすいです。一方で,Reverse KLは$\log$関数を$q$で重みづけしていますので,$q$は$0$ではない部分で$p$を網羅しようとします。その結果,$q$の分散は小さくなりやすいです。例えば,真の事後分布が多峰性の場合,Forward KLでは複数のピークをならしたような近似事後分布が得られるのに対し,Reverse KLではある1つのピークに着目した近似事後分布が得られやすいです。多峰性の場合は近似事後分布に混合正規分布を持ち出せばうまくフィッティングできますが,KLダイバージェンスの非対称性を把握しておくことは非常に大切です。VAEはReverse KLを利用しており,近似事後分布が真の事後分布よりも尖ってしまう可能性があるため,注意が必要です。
エンコーダ・デコーダの意味
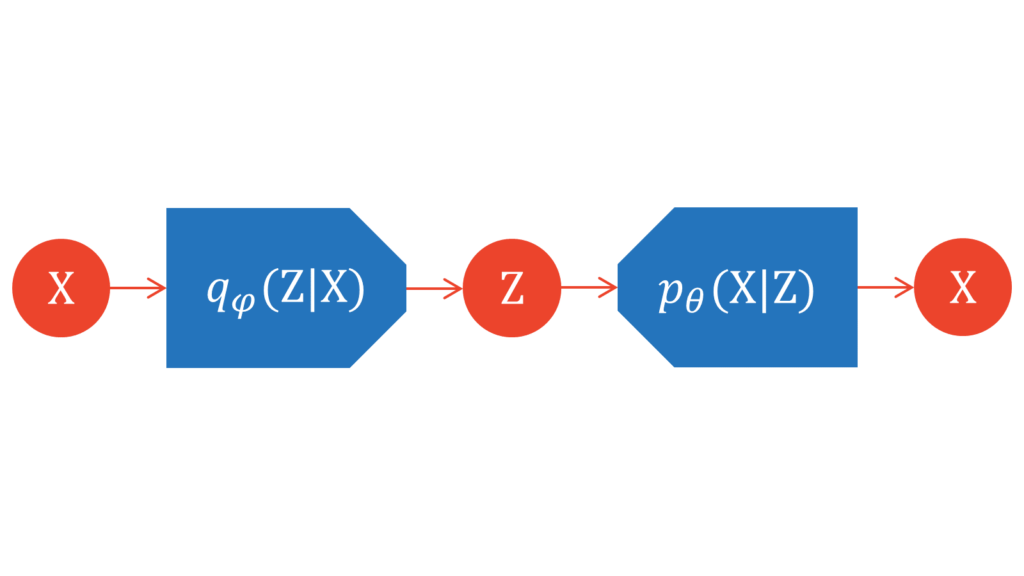
ここで改めて,近似事後分布$q_{\varphi}(Z|X)$と尤度関数$p(X|Z)$の関係性を図示してみましょう。
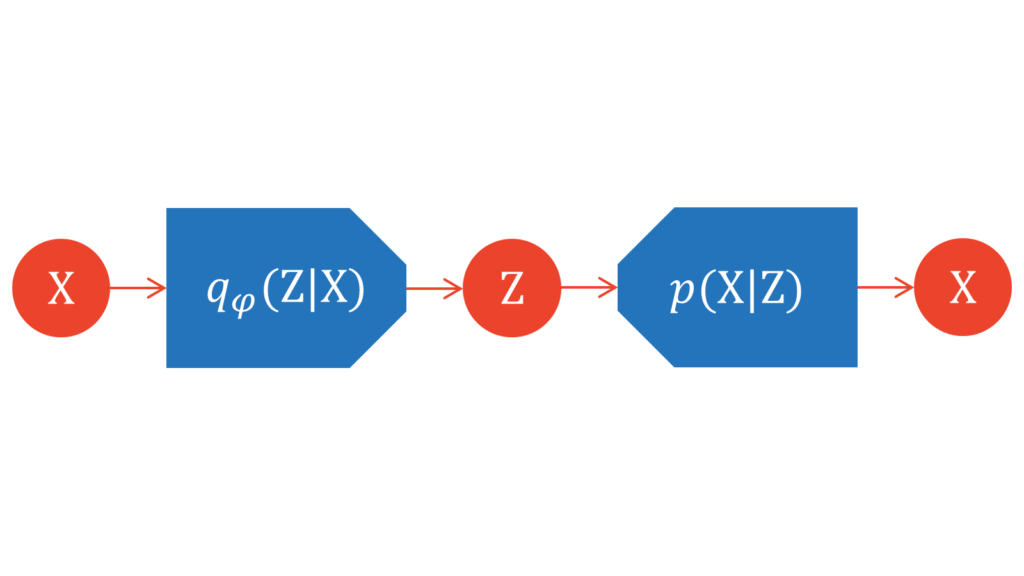
勘の良い方であれば気付くと思うのですが,図がオートエンコーダ型になっています。$X$を入力として受け取り,$X$を出力として吐き出しています。入力から出力までのフローが微分可能な形で繋がっていれば,教師なし学習が可能になります。
そのため,VAEでは真の分布$p$もDNNで学習可能な分布$p_{\theta}$であると設定します。
\calL_{\VAE}[q_{\varphi}(Z|X)] &= \ln p_{\theta}(X)-\left.KL[q_{\varphi}(Z|X) \right\| p_{\theta}(Z|X)]
\end{align}
真の分布が学習可能とすることで,変分ベイズにおいて一定値であった周辺対数尤度が可変値になります。
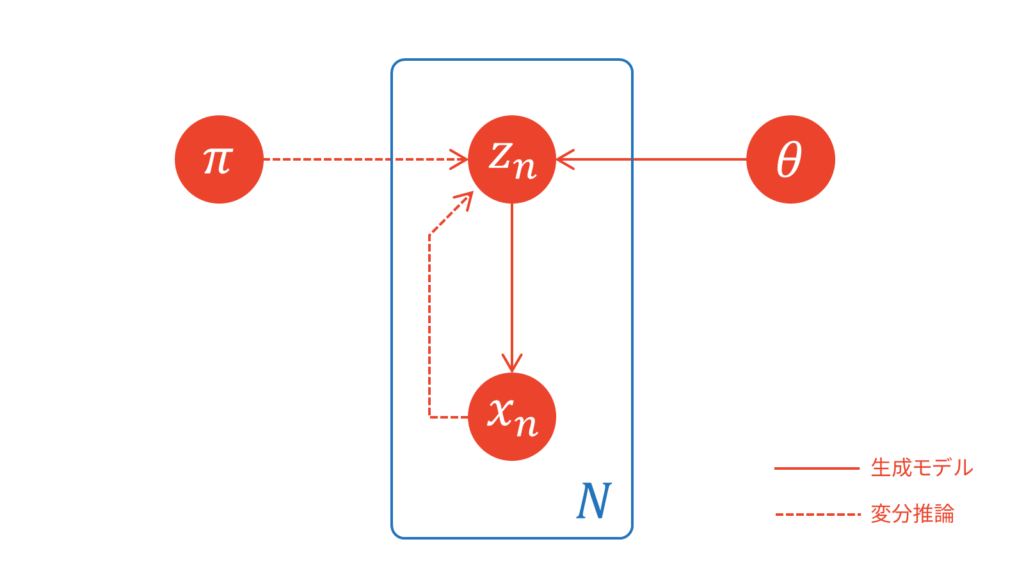
潜在変数とパラメータの依存関係を可視化するときは,一般的には以下のようなグラフィカルモデルが利用されます。機械学習分野の論文では,確率変数の生成過程を実線で,変分推論を用いた近似を破線で表すことが多いです。グラフィカルモデルを展開した図が,上でお見せしたようなオートエンコーダ型の図になると理解しておきましょう。
ここからは慣習に従って,VAEにおける近似事後分布をエンコーダ,尤度関数をデコーダと表記することにします。
分布をDNNで学習する
デコーダとエンコーダを学習可能な分布に設定したからと言って,全ての処理が微分可能になったわけではありません。ここで,少し考えてみたいことがあります。「分布をDNNで学習する」とはどのように実現すれば良いのでしょうか。
結論をお伝えしてしまうと,エンコーダ・デコーダがそれぞれ分布の形状を決定するパラメータを出力すればよいのです。具体的にパラメータを定めるため,本稿ではエンコーダとデコーダに以下を仮定します。
q_{\varphi}(Z|X) &= \N (\mu_{\varphi}, \sigma^2_{\varphi}) \\[0.7em]
p_{\theta} (X|Z) &= \mathrm{Bernoulli} (\lambda_{\theta})
\end{align}
なお,エンコーダとデコーダの分布は任意に定められます。適用する問題の種類によって,両者に適切な分布を設定する必要があります。エンコーダは特徴量抽出器として捉えることができますので,対象とする特徴量をよく観察して分布を定める必要があります。デコーダは入力変数をよく観察して分布を定める必要があります。今回は,特徴量は特に強い仮定を置かないためエンコーダとしてベーシックな正規分布,入力変数として2値変数を仮定するためデコーダとしてベルヌーイ分布を設定しました。例えば,入力変数がスペクトログラムなどの実数値であればデコーダにガウス分布を仮定しますし,非負値であれば指数分布やレイリー分布を仮定します。なお,VAEでは変分ベイズの枠組みにより潜在変数の事前分布を設定しますので,エンコーダの分布は計算を簡単にするため事前分布と同じ分布族に設定することが多いです。
近似事後分布には正規分布,潜在変数の尤度関数にはベルヌーイ分布を仮定しました。このとき,エンコーダからは$\mu_{\varphi}$と$\sigma_{\varphi}$が出力されることになります。
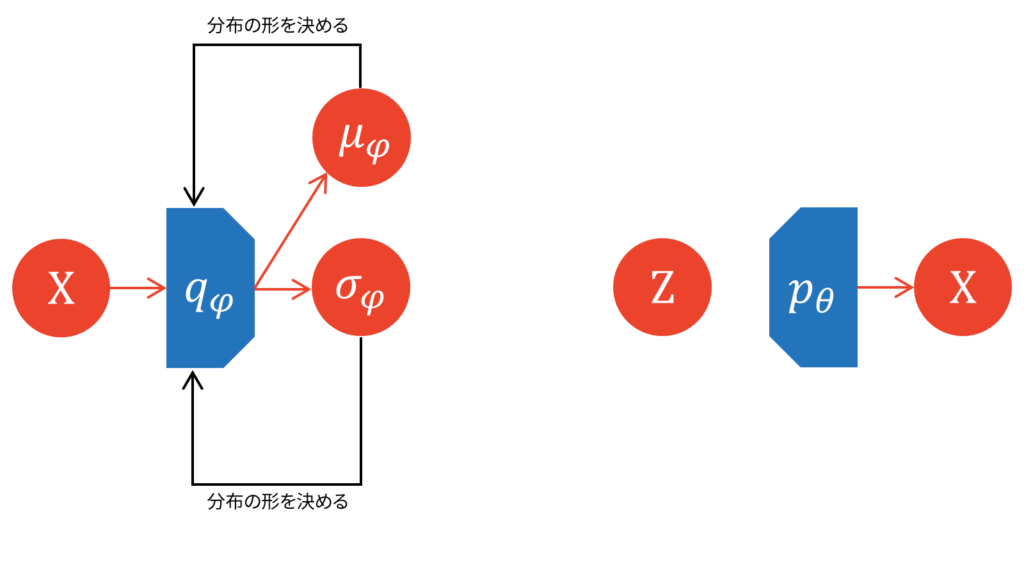
同様に,デコーダからは$\lambda_{\theta}$が出力されることになります。
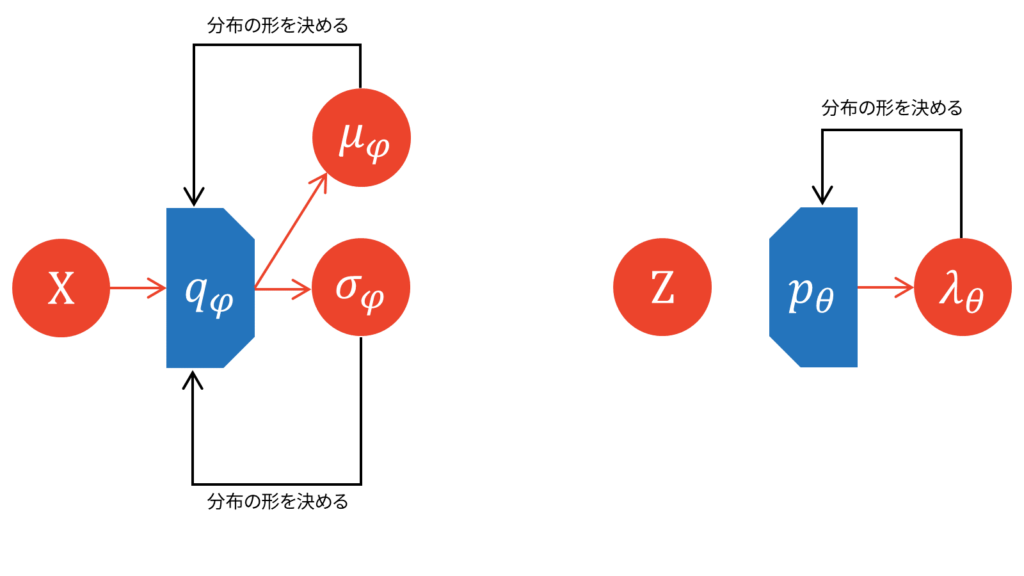
しかし,デコーダの受け付ける入力は$Z$です。そこで,エンコーダの出力したパラメータに従う確率分布から,微分可能な形で潜在変数$Z$をサンプリングする必要が出てきます。一般には,サンプリングという処理は微分不可能です。
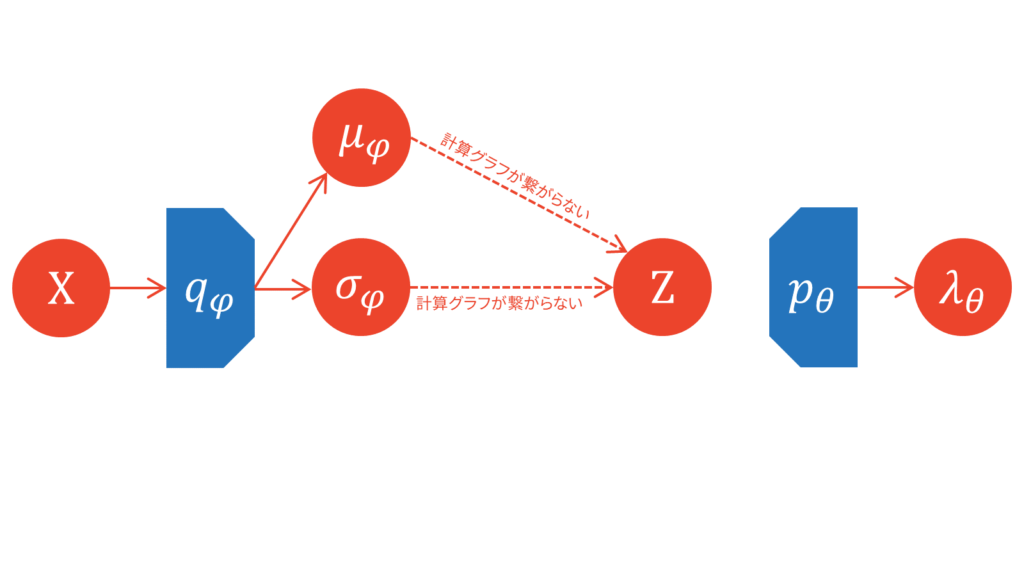
微分可能な疑似サンプリング
サンプリング処理の介在により誤差逆伝播を利用できないという問題を解決するため,KingmaらはReparameterization trickと呼ばれる決定的な式変形を提案しました。決定的な処理を用いて,エンコーダ$q_{\varphi}$からの疑似的なサンプリングを可能にします。目標は,
Z \sim \N (\mu_{\varphi}, \sigma^2_{\varphi})
\end{align}
なる潜在変数$Z$をサンプリングすることです。やや天下り的ですが,以下の式にしたがってエンコーダの分散$\tilde{\sigma}_{\varphi}$を決定的に生成します。
\varepsilon &\sim \mathcal{N}(0,1) \\[0.7em]
\tilde{\sigma}_{\varphi} &= \sigma_{\varphi} \cdot \varepsilon
\end{align}
正確に立式すると$X$と$Z$は多次元になりますので,$\tilde{\sigma}_{\varphi}$は$\varepsilon$との要素積$\odot$によって生成されます。本稿では,分かりやすさのため$X$は$1$次元であるものとし,多次元の場合の定式化は後ほど行うようにします。
このとき,決定的に生成された$\tilde{\sigma}_{\varphi}$を用いて,潜在変数$Z$を疑似的にサンプリングします。
Z &=\tilde{\sigma}_{\varphi} + \mu_{\varphi}
\end{align}
エンコーダには正規分布を仮定していましたので,エンコーダの形を定めるためには期待値と分散だけで必要十分です。期待値と分散の性質より,$Z$の期待値を求めてみましょう。
E[Z] &= E[\tilde{\sigma}_{\varphi} + \mu_{\varphi}] \\[0.7em]
&= E[\tilde{\sigma}_{\varphi}] + E[\mu_{\varphi}] \\[0.7em]
&= E[\sigma_{\varphi} \cdot \varepsilon] + E[\mu_{\varphi}] \\[0.7em]
&= E[\sigma_{\varphi}] \cdot E[\varepsilon] + E[\mu_{\varphi}] \\[0.7em]
&= E[\sigma_{\varphi}] \cdot 0 + \mu_{\varphi} \\[0.7em]
&= \mu_{\varphi}
\end{align}
同様に,期待値と分散の性質より,$Z$の分散を求めてみましょう。
V[Z] &= V[\tilde{\sigma}_{\varphi} + \mu_{\varphi}] \\[0.7em]
&= V[\tilde{\sigma}_{\varphi}] + V[\mu_{\varphi}]\quad (\because~\tilde{\sigma}_{\varphi}\text{と}\mu_{\varphi}\text{は独立}) \\[0.7em]
&= V[\sigma_{\varphi} \cdot \varepsilon] + V[\mu_{\varphi}] \\[0.7em]
&= \sigma^2_{\varphi} \cdot V[\varepsilon] + V[\mu_{\varphi}] \\[0.7em]
&= \sigma^2_{\varphi} \cdot 1 + 0 \\[0.7em]
&= \sigma^2_{\varphi}
\end{align}
以上より,$Z$はしっかりとエンコーダ$q_{\varphi}$にしたがっているとみなすことができます。
Z &\sim \N (\mu_{\varphi}, \sigma^2_{\varphi}) \\[0.7em]
&= q_{\varphi}(Z|X)
\end{align}
この決定的な処理を用いることで,エンコーダ(近似事後分布)とデコーダ(尤度関数)の処理が微分可能な形で繋がり,誤差逆伝播が可能になります。
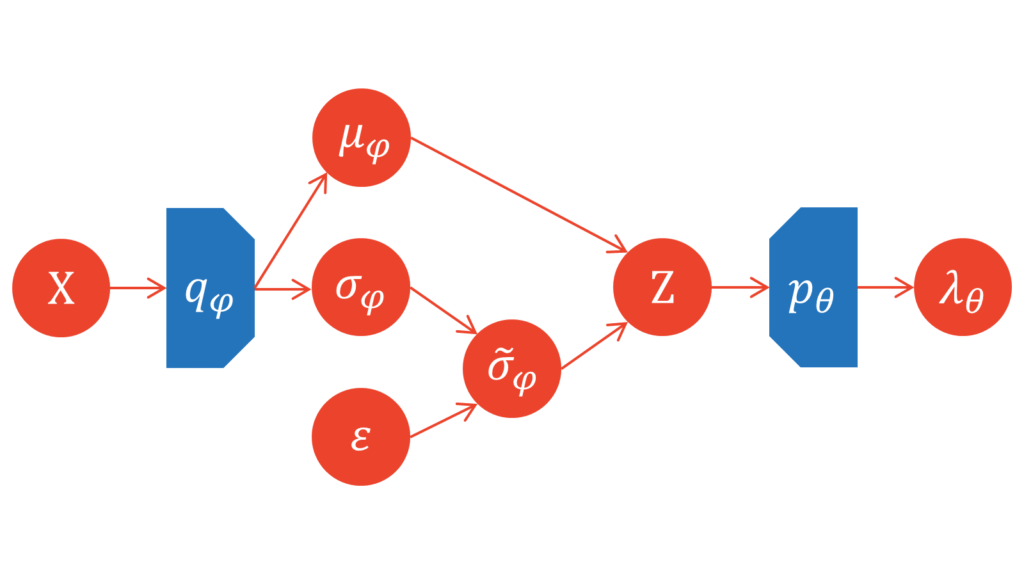
DNNで学習を行うということは,デコーダを定める$\varphi$とエンコーダを定める$\theta$は点推定されるということを意味しています。また,$\varphi$,$\theta$がイテレーションごとに更新されると,上限$\ln_{\theta}(X)$も変化します。この点が,VAEにEMアルゴリズム的な側面が含まれるという観点に繋がります。
EM・VBとの比較
さて,最初の表に戻ってみます。それぞれの行について確認していきましょう。

EMアルゴリズムは最尤推定を行うための手法であり,目的関数は対数尤度です。潜在変数とパラメータは明示的に分離します。上限は対数尤度であり,更新するパラメータに依存するため可変値です。Eステップではパラメータの計算で用いる負担率を求めておき,Mステップではラグランジュの未定乗数法などを用いてパラメータを点推定します。
変分ベイズは真の事後分布$p$の近似分布$q$を求めるための手法であり,KLダイバージェンスと下限という2つの等価な目的関数が存在します。変数は潜在変数のみであり,パラメータも確率変数として扱うために,明示的に潜在変数とパラメータの区別はしません。上限は周辺対数尤度であり,更新する確率変数に依存しないため一定値です。変分ベイズでは本質的にはEステップしか存在しないと捉えられますが,あえて潜在変数とパラメータを区別すれば,変分Eステップでは潜在変数に関する期待値を求め,変分Mステップでは潜在変数以外に関する期待値を求める操作を行います。
VAEのアイディアは変分ベイズから出発します。変分ベイズの目的関数は,KLダイバージェンスもしくは下限です。しかし,VAEでは近似事後分布を$q$ではなく$q_{\varphi}$として考えるため,目的関数がパラメータ$\varphi$に依存して可変値になります。潜在変数とそれ以外のパラメータは明示的に区別します。上限は周辺対数尤度でしたが,パラメータ$\theta$に依存するため可変値です。$\theta$,$\varphi$はReparameterization trickによって誤差逆伝播に基づく最適化が行われるため,点推定されます。
変分ベイズでEステップとMステップを区別する必要がないという主張は,VAEにおいてはより顕著に現れます。VAEでは変分下限が大きくなる方向に確率的勾配法を利用して一気通貫にパラメータを推定しますので,EステップとMステップという分類が意味を成しません。
MNISTへの適用
本章では,機械学習の分野における比較的簡単なデータセットとしてデファクトスタンダードとなっているMNISTを題材に,VAEの適用方法をお伝えしていきます。MNISTは手書き0~9までの数字の画像データセットで,6万枚の訓練データと1万枚のテストデータから構成されます。

MNISTでは全ての画像には正解ラベルが付与されているため,画像を入力として受け取りラベルを出力する識別モデルの評価に利用することができます。一方で,本章の目的はVAEの仕組みとその成り立ちをお伝えすることですので,VAEを識別モデルとして利用するのではなく,VAEを教師なし学習して潜在空間の構成を詳しく観察していきます。
確率モデルとしての定式化
最初は確率変数の定義を行います。入力$X$と潜在変数$Z$は以下のように設定します。
X &= \{X_1, \ldots, X_N\} \\[0.7em]
Z &= \{Z_1, \ldots, Z_D\}
\end{align}
ただし,$N$個のサンプルは互いに独立であると仮定します。
MNISTの場合$N$はセルに対応するため,$N=28 \times 28 = 784$となります。手書き数字の白黒は隣り合うセルに依存していると考えられるため,本来は各セルが独立でないと仮定する方が妥当でしょう。しかし,エンコーダで特徴量(潜在変数)を抽出する際に隣り合うセルの情報も抽出されるために,各セル独立にベルヌーイ分布に従うとはいえ,セルの依存関係も踏まえた推定が可能である点に注意してください。
変分ベイズでは近似事後分布$q(Z)$を考えましたが,VAEでは近似事後分布$q(Z|X)$を考えます。
q_{\varphi}(Z|X) \sim p_{\theta}(Z|X)
\end{align}
確率モデルの問題を考える出発点は,同時分布を設計することです。
p_{\theta}(X, Z) &= p_{\theta}(X|Z)p(Z)
\end{align}
ただし,事前分布はDNNに依存しないため,$p_{\theta}(Z)$ではなく$p(Z)$と表記しています。今回は,同時分布と近似事後分布の形状を以下のように定めます。
p_{\theta}(X|Z) &= \mathrm{Bernoulli}(\vlambda_{\theta}) \\[0.7em]
p(Z) &= \N (\vzero, \mI) \\[0.7em]
q_{\varphi}(Z|X) &= \N (\vmu_{\varphi}, \mSigma_{\varphi})
\end{align}
ただし,$\vlambda_{\theta} \in [0, 1]^{N}$は$N$個のセルのベルヌーイ分布のパラメータを結合したベクトル,$\mSigma_{\varphi}$は以下のような分散共分散行列を表し,$[\cdot]_{n}$は$n$番目の要素を表します。
\mSigma_{\varphi} &=
\begin{pmatrix}
\left[\sigma_{\varphi}^2\right]_{1} & 0 & \dots & 0 \\
0 & \left[\sigma_{\varphi}^2\right]_{2} & \dots & 0 \\
\vdots & \vdots & \ddots & \vdots \\
0 & 0 & \dots & \left[\sigma_{\varphi}^2\right]_{D}
\end{pmatrix}
\end{align}
まず,$N$個のサンプルは互いに独立ですので,ベルヌーイ分布の確率質量関数に注意すると,デコーダは以下のように表されます。
p_{\theta}(X|Z) &= \prod_{n=1}^{N}\left[\lambda_{\theta}\right]_{n}^{x} \left( 1-\left[\lambda_{\theta}\right]_{n} \right)^{1-x}
\end{align}
以下では,これらの分布を定めた根拠を説明しておきます。
今回の学習対象はMNISTですので,白黒画像と捉えると各セルは$[0, 1]$の値の実数値となります。ただし,$0$に近いほど黒,$1$に近いほど白を表すものとします。すると,各セルの値は$\lambda_{\theta}\in[0, 1]$をパラメータとするベルヌーイ分布に従うと考えられます。ゆえに,真の尤度関数(デコーダ)はベルヌーイ分布として定めています。
最もベーシックな潜在変数の事前分布は,標準正規分布です。潜在空間に多峰性を仮定する場合や,正規分布以外の分布を仮定する場合以外では,特に理由がなければ標準正規分布にすると計算が簡単になります。近似事後分布の設定ですが,計算を簡単にするために事前分布と同じ分布族を設定することが多いです。今回もそれに倣って,近似事後分布に正規分布を仮定します。近似事後分布の形状はデコーダの出力が定めることに注意してください。
VAEの下限は,再構成誤差と負のKLダイバージェンスで表されるのでした。
\calL_{\VAE}[q_{\varphi}(Z|X)] &= E_{q_{\varphi}}\left[ \log p_{\theta}(X|Z) \right]-\left.\KL\left[ q_{\varphi}(Z|X) \right\| p(Z) \right]
\end{align}
結論からお伝えすると,上記仮定を置く場合,変分下限は以下のように表されます。
\calL_{\VAE}[q_{\varphi}(Z|X)]
&= \sum_{n=1}^{N} \left\{ x_{n}\log \left[\lambda_{\theta}\right]_{n} + (1-x_{n})\log\left(1-\left[\lambda_{\theta}\right]_{n}\right)\right\} \notag \\[0.7em]
&\quad\quad+\frac{1}{2} \sum_{d=1}^{D} \left( 1 + \log \left[\sigma_{\varphi}^2\right]_{d}-\left[\sigma_{\varphi}^2\right]_{d}-\left[\mu^2_{\varphi}\right]_{d} \right)
\end{align}
以下では,式($\ref{eq_L_VAE}$)における第一項目の再構成誤差と,第二項目の負のKLダイバージェンスをそれぞれ計算していきます。
第一項目:再構成誤差
第一項目の再構成誤差に,上で仮定した分布を代入してみましょう。
E_{q_{\varphi}}\left[ \log p_{\theta}(X|Z) \right] &= \int_{Z} q_{\varphi}(Z|X) \log p_{\theta}(X|Z) dZ \\[0.7em]
&= \int_{Z_{1}}\ldots\int_{Z_{D}} q_{\varphi}(Z|X) \log p_{\theta}(X|Z) dZ_{1} \ldots dZ_{D} \label{eq_reconstruction_int}
\end{align}
一般に,積分計算は煩雑になりやすく,計算量も膨大になりやすいです。例えば,バッチ数を$B$,各潜在変数が離散型で$K$種類の値を取り得ると仮定すると,式($\ref{eq_reconstruction_int}$)の計算量は以下のようになります。
O(K^{BD})
\end{align}
バッチ数と潜在変数の次元数に関して指数関数的に計算量が増加することが分かります。たとえ,バッチ数を$1$に設定したとしても,VAEに十分な表現力を担保させるためには潜在変数として比較的大きな次元数を設定することが多いです。したがって,式($\ref{eq_reconstruction_int}$)の計算には何らかの近似手法が必要になります。
最もベーシックなVAEでは,モンテカルロ法を利用します。モンテカルロ法とは,積分計算を離散有限サンプルの平均で表すシンプルな近似です。
以下の$D$重積分を考える。
I &= \int_{a}^{b} \ldots \int_{a}^{b} f(x_1, \ldots, x_D) dx_{1} \ldots dx_{D}
\end{align}
$[a, b]$上の一様分布に従う確率変数$X$を$D \times L$個抽出すると,$I$は以下のように近似できる。
I &\sim \frac{1}{L} \sum_{l=1}^{L} f(X_{1, l}, \ldots, X_{D, L})
\end{align}
特に,$L=1$の場合は$X$を$D$個抽出することで$I$を$O(1)$で計算できる。
I &\sim f(X_{1}, \ldots, X_{D})
\end{align}
本稿ではモンテカルロ法の「数学的な厳密性」と「計算量の厳密性」は範疇外とします。例えば,上で紹介したモンテカルロ法では一様分布に従う確率変数をサンプリングしていますが,正規分布など別の分布を仮定した近似手法もモンテカルロ法と呼ぶことにします。他にも,計算量を考える場合は時間計算量と空間計算量の区別を行うべきですし,乱数を生成する計算量も考慮するべきなのですが,これらは本稿の趣旨とは逸れるために範疇外としています。VAEの学習では,一般にバッチ学習が行われることや十分なエポック数訓練されることなどから,$L=1$のモンテカルロ法がよく利用されます。
式($\ref{eq_reconstruction_int}$)に$L=1$のモンテカルロ法を適用することを考えましょう。VAEのモンテカルロ法は,乱数がエンコーダ(正規分布)に従っているケースに相当します。しかし,エンコーダからのサンプリング操作は微分不可能ですので誤差逆伝播することができませんでした。そこで,KingmaらはReparameterization trickによって,潜在変数のエンコーダからの疑似的なサンプリングを可能にしたのでした。
式($\ref{eq_reconstruction_int}$)に$L=1$のモンテカルロ法を適用した結果は,以下のようになります。
E_{q_{\varphi}}\left[ \log p_{\theta}(X|Z) \right] &\sim \log \left\{\prod_{n=1}^{N}\left[\lambda_{\theta}\right]_{n}^{x} \left( 1-\left[\lambda_{\theta}\right]_{n} \right)^{1-x}\right\} \\[0.7em]
&= \sum_{n=1}^{N} \left\{ x_{n}\log \left[\lambda_{\theta}\right]_{n} + (1-x_{n})\log\left(1-\left[\lambda_{\theta}\right]_{n}\right) \right\}
\end{align}
第一項目の再構成誤差は,負のバイナリクロスエントロピーと等価になりました。負のバイナリクロスエントロピーは,尤度関数にベルヌーイ分布を仮定した場合の対数尤度と等価でしたので,当然と言えば当然の結果です。なお,尤度関数にベルヌーイ分布を仮定する多くのVAEの実装では,再構成誤差の計算でバイナリクロスエントロピー関数を利用していますが,本稿の実装では素直に成分計算しています。
第二項目:KLダイバージェンス
第二項目の負のKLダイバージェンスを計算しましょう。愚直に計算すると少し大変なので,今回は多変量正規分布間のKLダイバージェンスの計算結果を利用しましょう。
確率変数$X=\{ X_{1}, \ldots, X_{D} \}$に対して定義される
p(X) &\sim \N (\vmu_{p}, \Sigma_{p}) \\[0.7em]
q(X) &\sim \N (\vmu_{q}, \Sigma_{q})
\end{align}
に対して,以下が成り立つ。
&\left. \KL \left[ q(X) \right\| p(X) \right] \notag \\[0.7em]
&= \frac{1}{2} \left\{ \log \frac{|\Sigma_p|}{|\Sigma_q|}
+ \Tr \left[ \Sigma_{p}^{-1} \Sigma_{q} \right]
+ \left( \vmu_q-\vmu_p \right)^T \Sigma_{p}^{-1} \left( \vmu_q-\vmu_p \right)-D
\right\} \label{eq_KL_gaussian}
\end{align}
ただし,$|\cdot|$は行列式を表す。
詳しい導出は,以下をご覧ください。
今回は,以下のパラメータが仮定されています。
(\vmu_p, \Sigma_p) &= (\vzero, \mI) \\[0.7em]
(\vmu_q, \Sigma_q) &= (\vmu_{\varphi}, \mSigma_{\varphi})
\end{align}
このとき,式($\ref{eq_KL_gaussian}$)の各項を計算しましょう。式($\ref{eq_KL_gaussian}$)の第一項目は,以下のように計算されます。
\log \frac{|\Sigma_p|}{|\Sigma_q|} &= -\log \left|\mSigma_{\varphi}\right| \\[0.7em]
&= -\log \prod_{d=1}^{D}\left[\sigma_{\varphi}^2\right]_{d} \\[0.7em]
&= -\sum_{d=1}^{D} \log \left[\sigma_{\varphi}^2\right]_{d}
\end{align}
式($\ref{eq_KL_gaussian}$)の第二項目は,以下のように計算されます。
\Tr \left[ \Sigma_{p}^{-1} \Sigma_{q} \right] &= \Tr \left[ \mSigma_{\varphi}\right] \\[0.7em]
&= \sum_{d=1}^{D} \left[\sigma_{\varphi}^2\right]_{d}
\end{align}
式($\ref{eq_KL_gaussian}$)の第三項目は,以下のように計算されます。
\left( \vmu_q-\vmu_p \right)^T \Sigma_{p}^{-1} \left( \vmu_q-\vmu_p \right)
&= \left( \vmu_{\varphi}-0 \right)^T \cdot \mI^{-1} \cdot \left( \vmu_{\varphi}-0 \right) \\[0.7em]
&= \vmu_{\varphi}^T \vmu_{\varphi} \\[0.7em]
&= \sum_{d=1}^{D} \left[\mu^2_{\varphi}\right]_{d}
\end{align}
以上の結果を,式($\ref{eq_KL_gaussian}$)に代入しましょう。
-&\left. \KL \left[ q_{\varphi}(Z|X) \right\| p(Z) \right] \notag \\[0.7em]
&= -\frac{1}{2}\left\{
-\sum_{d=1}^{D} \log \left[\sigma_{\varphi}^2\right]_{d}
+ \sum_{d=1}^{D} \left[\sigma_{\varphi}^2\right]_{d}
+ \sum_{d=1}^{D} \left[\mu^2_{\varphi}\right]_{d}-D
\right\} \\[0.7em]
&= \frac{1}{2} \sum_{d=1}^{D} \left( 1 + \log \left[\sigma_{\varphi}^2\right]_{d}-\left[\sigma_{\varphi}^2\right]_{d}-\left[\mu^2_{\varphi}\right]_{d} \right)
\end{align}
以上より,VAEの下限は以下のように表されます。
\calL_{\VAE}[q_{\varphi}(Z|X)] &= E_{q_{\varphi}}\left[ \log p_{\theta}(X|Z) \right]-\left.\KL\left[ q_{\varphi}(Z|X) \right\| p(Z) \right] \\[0.7em]
&= \sum_{n=1}^{N} x_{n}\log \left[\lambda_{\theta}\right]_{n} + (1-x_{n})\log\left(1-\left[\lambda_{\theta}\right]_{n}\right) \notag \\[0.7em]
&\quad\quad+ \frac{1}{2} \sum_{d=1}^{D} \left( 1 + \log \left[\sigma_{\varphi}^2\right]_{d}-\left[\sigma_{\varphi}^2\right]_{d}-\left[\mu^2_{\varphi}\right]_{d} \right)
\end{align}
実装
本章では,前章でお伝えしたVAEのMNISTへの適用方法に基づいて,VAEを実装していきます。実験の一例を先にお伝えしておくと,任意の潜在変数を利用することで,以下のような手書き数字の変化を確認することができます。

実装はGithubで公開しています。以下のコマンドでMNISTをVAEで学習することができます。
python main.py main --z_dim [潜在変数の次元数]ソースコードのコメントは英語で書いています。これはGithubで公開する際に,外国の方々にも参考にしていただきたいからです。コメント規則であるdocstringはGoogleスタイルを利用しています。
ここからは,以下の形式でメソッド単位で解説を行っていきます。
[メソッド名・その他タイトルなど]
# ソースコード[ソースコードの解説]
データの準備
以下では,MNISTを利用する準備を行います。torchvisionを利用すれば,わざわざ公式HPからデータをダウンロードして整備しなくても,簡単にMNISTを利用する準備を行うことができます。
import os # tensorboardの出力先作成
import matplotlib.pyplot as plt # 可視化
import numpy as np # 計算
import torch # 機械学習フレームワークとしてpytorchを使用
import torch.nn as nn # クラス内で利用するモジュールのため簡略化
import torch.nn.functional as F # クラス内で利用するモジュールのため簡略化
from torch import optim # 最適化アルゴリズム
from torch.utils.tensorboard import SummaryWriter # tensorboardの利用
from torchvision import datasets, transforms # データセットの準備標準的なライブラリをインポートします。
# tensorboardのログの保存先
if not os.path.exists("./logs"):
os.makedirs("./logs")本実装では,tensorboardを利用してlossのモニタリングを行います。そのため,tensorboardが参照するログの格納先を予め作成しておきます。
# MNISTのデータをとってくるときに一次元化する前処理
transform = transforms.Compose([transforms.ToTensor(), transforms.Lambda(lambda x: x.view(-1))])
# trainデータとtestデータに分けてデータセットを取得
dataset_train_valid = datasets.MNIST("./", train=True, download=True, transform=transform)
dataset_test = datasets.MNIST("./", train=False, download=True, transform=transform)
# trainデータの20%はvalidationデータとして利用
size_train_valid = len(dataset_train_valid) # 60000
size_train = int(size_train_valid * 0.8) # 48000
size_valid = size_train_valid - size_train # 12000
dataset_train, dataset_valid = torch.utils.data.random_split(dataset_train_valid, [size_train, size_valid])
# 取得したデータセットをDataLoader化する
dataloader_train = torch.utils.data.DataLoader(dataset_train, batch_size=1000, shuffle=True)
dataloader_valid = torch.utils.data.DataLoader(dataset_valid, batch_size=1000, shuffle=False)
dataloader_test = torch.utils.data.DataLoader(dataset_test, batch_size=1000, shuffle=False)torchvisionを利用してMNISTを利用する準備を行います。取得できるデータは,デフォルトでは訓練データとテストデータに分けられています。今回は,学習を停止させるタイミングを判断するために検証データを利用するため,学習データの20%を検証データとしてあらかじめ分離させておきます。結局,訓練・検証・テストデータの内訳は以下の通りです。
- 訓練データ:48000枚
- 検証データ:12000枚
- テストデータ:10000枚
また,バッチ学習を簡単に行うため,pytorchのDataloaderを利用します。バッチサイズとシャッフルの有無を指定してインスタンス化すれば,指定したバッチサイズでイテレーションを行ってくれるDataloaderが生成されます。
VAEクラスの実装
class VAE(nn.Module):ここからは,VAEクラスを定義していきます。pytorchでクラスを定義する際は,nn.Moduleを継承する必要があります。
コンストラクタ
def __init__(self, z_dim):
"""コンストラクタ
Args:
z_dim (int): 潜在空間の次元数
Returns:
None.
Note:
eps (float): オーバーフローとアンダーフローを防ぐための微小量
"""
super(VAE, self).__init__() # VAEクラスはnn.Moduleを継承しているため親クラスのコンストラクタを呼ぶ必要がある
self.eps = np.spacing(1) # オーバーフローとアンダーフローを防ぐための微小量
self.x_dim = 28 * 28 # MNISTの場合は28×28の画像であるため
self.z_dim = z_dim # インスタンス化の際に潜在空間の次元数は自由に設定できる
self.enc_fc1 = nn.Linear(self.x_dim, 400) # エンコーダ1層目
self.enc_fc2 = nn.Linear(400, 200) # エンコーダ2層目
self.enc_fc3_mean = nn.Linear(200, z_dim) # 近似事後分布の平均
self.enc_fc3_logvar = nn.Linear(200, z_dim) # 近似事後分布の分散の対数
self.dec_fc1 = nn.Linear(z_dim, 200) # デコーダ1層目
self.dec_fc2 = nn.Linear(200, 400) # デコーダ2層目
self.dec_drop = nn.Dropout(p=0.2) # 過学習を防ぐために最終層の直前にドロップアウト
self.dec_fc3 = nn.Linear(400, self.x_dim) # デコーダ3層目コンストラクタではネットワーク構造の定義を行います。今回は,VAEのエンコーダとデコーダに以下のようなネットワークを採用します。
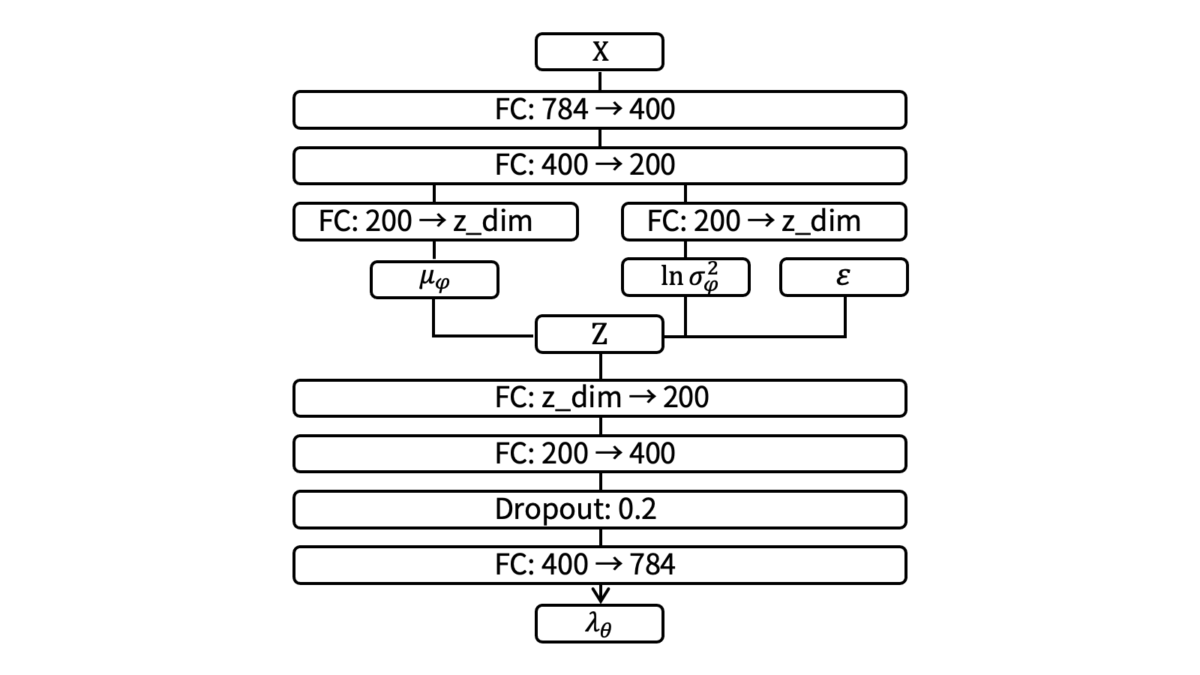
全結合層のみから構成される非常にシンプルなネットワークです。設計にはいくつかのポイントがあります。まず,エンコーダが分散を出力する部分は分散の対数を出力するようにします。これは,分散に非負制約があるためです。softplusなどを利用すれば,非負制約を満たしたうえで分散そのものを出力するように設計することはできますが,無理に非負制約がある変数を利用する理由もありませんし,pytorchのVAE実装例でも分散の対数を出力するようにしていることを踏まえると,上記設定が自然と思われます。
エンコーダ
def encoder(self, x):
"""エンコーダ
Args:
x (torch.tensor): (バッチサイズ, 入力次元数)サイズの入力データ
Returns:
mean (torch.tensor): 近似事後分布の平均
logvar (torch.tensor): 近似事後分布の分散の対数
"""
x = F.relu(self.enc_fc1(x))
x = F.relu(self.enc_fc2(x))
return self.enc_fc3_mean(x), self.enc_fc3_logvar(x)コンストラクタで定義したネットワークを用いてエンコーダを定義します。活性化関数にはReLUを利用します。
潜在変数のサンプリング
def sample_z(self, mean, log_var, device):
"""Reparameterization trickに基づく潜在変数Zの疑似的なサンプリング
Args:
mean (torch.tensor): 近似事後分布の平均
logvar (torch.tensor): 近似事後分布の分散の対数
device (String): GPUが使える場合は"cuda"でそれ以外は"cpu"
Returns:
z (torch.tensor): (バッチサイズ, z_dim)サイズの潜在変数
"""
epsilon = torch.randn(mean.shape, device=device)
return mean + epsilon * torch.exp(0.5 * log_var)Reparameterization trickに基づく潜在変数の疑似的なサンプリングを定義します。
デコーダ
def decoder(self, z):
"""デコーダ
Args:
z (torch.tensor): (バッチサイズ, z_dim)サイズの潜在変数
Returns:
y (torch.tensor): (バッチサイズ, 入力次元数)サイズの再構成データ
"""
z = F.relu(self.dec_fc1(z))
z = F.relu(self.dec_fc2(z))
z = self.dec_drop(z)
return torch.sigmoid(self.dec_fc3(z))コンストラクタで定義したネットワークを用いてデコーダを定義します。 エンコーダ同様,活性化関数にはReLUを利用します。
順伝播処理
def forward(self, x, device):
"""順伝播処理
Args:
x (torch.tensor): (バッチサイズ, 入力次元数)サイズの入力データ
device (String): GPUが使える場合は"cuda"でそれ以外は"cpu"
Returns:
KL (torch.float): KLダイバージェンス
reconstruction (torch.float): 再構成誤差
z (torch.tensor): (バッチサイズ, z_dim)サイズの潜在変数
y (torch.tensor): (バッチサイズ, 入力次元数)サイズの再構成データ
"""
mean, log_var = self.encoder(x.to(device)) # encoder部分
z = self.sample_z(mean, log_var, device) # Reparameterization trick部分
y = self.decoder(z) # decoder部分
KL = 0.5 * torch.sum(1 + log_var - mean**2 - torch.exp(log_var)) # KLダイバージェンス計算
reconstruction = torch.sum(x * torch.log(y + self.eps) + (1 - x) * torch.log(1 - y + self.eps)) # 再構成誤差計算
return [KL, reconstruction], z, y今まで定義してきたメソッドを利用してネットワークの順伝播処理を記述します。logを取る部分ではアンダーフローを防ぐために微小量を加えている点に注意してください。
モデルの学習
上で定義したVAEクラスをインスタンス化して学習させましょう。
モデルのインスタンス化
# GPUが使える場合はGPU上で動かす
device = torch.device("cuda" if torch.cuda.is_available() else "cpu")
# VAEクラスのコンストラクタに潜在変数の次元数を渡す
model = VAE(2).to(device)本稿では,潜在変数を可視化しやすくするために次元数は2に設定します。また,モデルの表現力の違いを確かめるために次元数を10と20に設定したモデルも,別途インスタンス化して学習させておきます。
学習の準備
# 今回はoptimizerとしてAdamを利用
optimizer = optim.Adam(model.parameters(), lr=0.001)
# 最大更新回数は1000回
num_epochs = 1000
# 検証データのロスとその最小値を保持するための変数を十分大きな値で初期化しておく
loss_valid = 10 ** 7
loss_valid_min = 10 ** 7
# early stoppingを判断するためのカウンタ変数
num_no_improved = 0
# tensorboardに記録するためのカウンタ変数
num_batch_train = 0
num_batch_valid = 0
# tensorboardでモニタリングする
writer = SummaryWriter(log_dir="./logs")モデルのoptimizerにはAdamを利用します。学習率は$10^{-3}$とします。最大更新回数は$1000$回とし,$10$回連続で検証データのlossが下がらなかった場合に学習を停止させます(early stopping)。また,tensorboardでモニタリングを行うためにwriterをインスタンス化しておきます。
学習イテレーション
# 学習開始
for num_iter in range(num_epochs):
model.train() # 学習前は忘れずにtrainモードにしておく
for x, t in dataloader_train: # dataloaderから訓練データを抽出する
lower_bound, _, _ = model(x, device) # VAEにデータを流し込む
loss = -sum(lower_bound) # lossは負の下限
model.zero_grad() # 訓練時のpytorchのお作法
loss.backward()
optimizer.step()
writer.add_scalar("Loss_train/KL", -lower_bound[0].cpu().detach().numpy(), num_iter + num_batch_train)
writer.add_scalar("Loss_train/Reconst", -lower_bound[1].cpu().detach().numpy(), num_iter + num_batch_train)
num_batch_train += 1
num_batch_train -= 1 # 次回のエポックでつじつまを合わせるための調整
# 検証開始
model.eval() # 検証前は忘れずにevalモードにしておく
loss = []
for x, t in dataloader_valid: # dataloaderから検証データを抽出する
lower_bound, _, _ = model(x, device) # VAEにデータを流し込む
loss.append(-sum(lower_bound).cpu().detach().numpy())
writer.add_scalar("Loss_valid/KL", -lower_bound[0].cpu().detach().numpy(), num_iter + num_batch_valid)
writer.add_scalar("Loss_valid/Reconst", -lower_bound[1].cpu().detach().numpy(), num_iter + num_batch_valid)
num_batch_valid += 1
num_batch_valid -= 1 # 次回のエポックでつじつまを合わせるための調整
loss_valid = np.mean(loss)
loss_valid_min = np.minimum(loss_valid_min, loss_valid)
print(f"[EPOCH{num_iter + 1}] loss_valid: {int(loss_valid)} | Loss_valid_min: {int(loss_valid_min)}")
# もし今までのlossの最小値よりも今回のイテレーションのlossが大きければカウンタ変数をインクリメントする
if loss_valid_min < loss_valid:
num_no_improved += 1
print(f"{num_no_improved}回連続でValidationが悪化しました")
# もし今までのlossの最小値よりも今回のイテレーションのlossが同じか小さければカウンタ変数をリセットする
else:
num_no_improved = 0
torch.save(model.state_dict(), f"./z_{model.z_dim}.pth")
# カウンタ変数が10回に到達したらearly stopping
if (num_no_improved >= 10):
print(f"{num_no_improved}回連続でValidationが悪化したため学習を止めます")
break
# tensorboardのモニタリングも停止しておく
writer.close()上で定義したDataloaderを利用してモデルの学習と検証を行います。コードが長くなっていますが,行っていることはシンプルで,Dataloaderからデータを取ってきて順伝播・逆伝播を行いパラメータを更新しているだけです。
tensorboardでlossをモニタリングするためにはwriterオブジェクトのadd_scalarメソッドを呼び出して各イテレーションの値を書き出す必要があります。今回は,バッチ単位でlossを書き出すようにしました。データセットが巨大な場合はバッチごとに値を書き出してしまうと莫大な量のログが残ってしまいますので,各エポックごとに書き出した方が無難でしょう。
検証データでlossを評価する前に,model.evalメソッドを呼び出すことを忘れないようにしましょう。trainモードのモデルのまま順伝播を行ってしまうと,ドロップアウトがそのまま機能してしまいます。他にも,batch normの制御などが行われます。early stoppingの実装には色々な方法がありますが,今回はシンプルにカウンタ変数を用意して分岐を実装しました。
コンソールで以下のコードを実行してtensorboardを起動しておきましょう。tensorboardはlocalhost上で立ち上がりますので,http://localhost:6006/にアクセスすれば確認することができます。
cd [プロジェクトへのパス]
tensorboard --logdir ./logsなお,Google colaboratoryを利用している場合は以下のコードでセル上にtensorboardを起動することができます。
%load_ext tensorboard
%tensorboard --logdir ./logs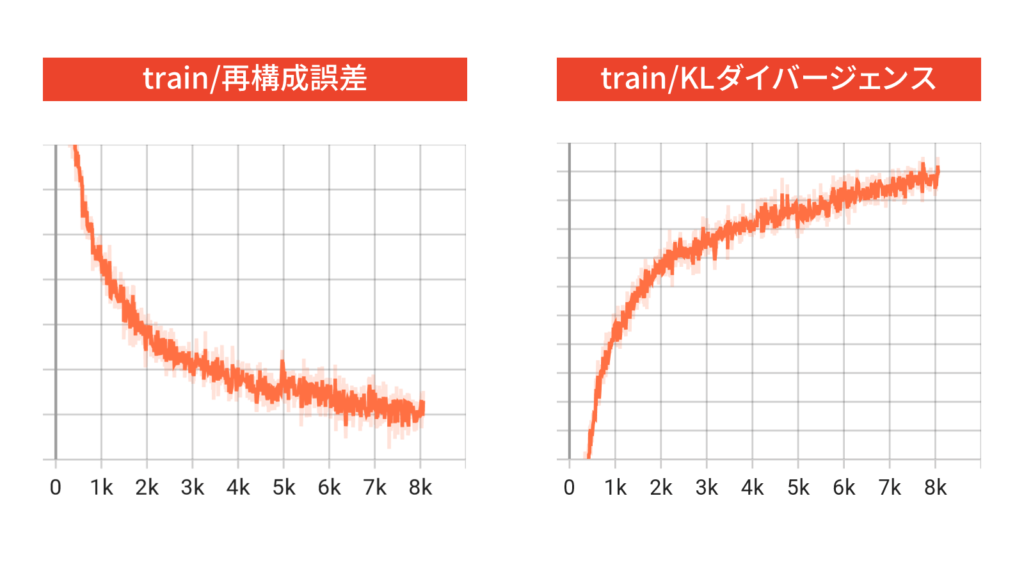
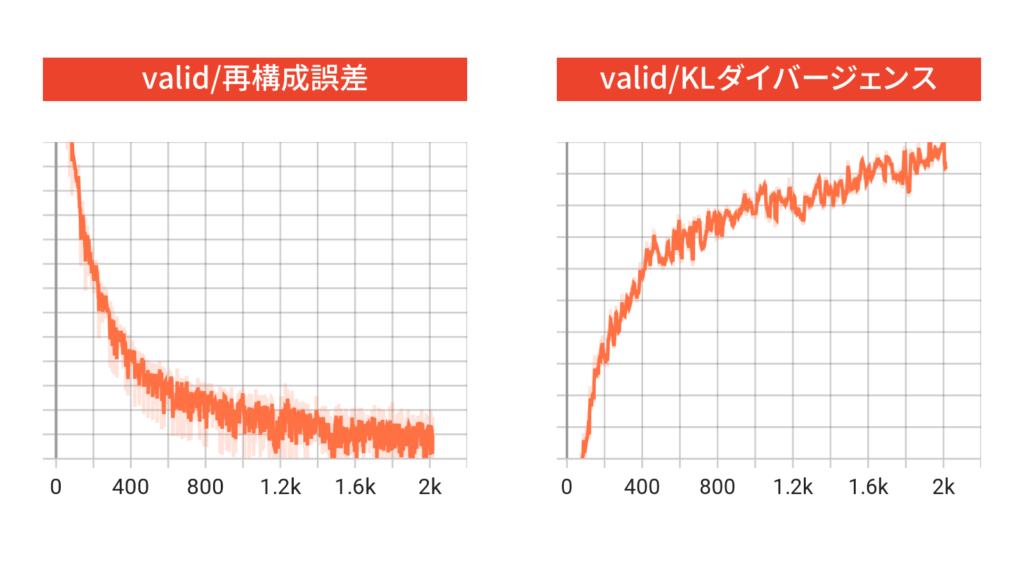
訓練データと検証データで横軸が異なるのは,バッチ数が異なるからです。訓練データと検証データのどちらにおいても,再構成誤差が減少していて,KLダイバージェンスが増加していることが分かります。これは,lossに対して再構成誤差の方が寄与していたため,ネットワークが再構成誤差を小さくする方に重点を置いて学習したためだと思われます。これは不思議な挙動ではなく,もしKLダイバージェンスの正則化項がなければもっとKLダイバージェンスが大きく発散していたと思われます。
なお,学習初期に再構成誤差よりもKLダイバージェンスの方が相対的に大きくなってしまうと,潜在変数の事後分布と事前分布が一致してしまうposterior collapseと呼ばれる現象が起きてしまい,データをうまく再構成することができなくなってしまうことがあります。posterior collapseを防ぐためには,学習初期はKLダイバージェンスの項を小さく重みづけをして,徐々に大きくしていくという工夫をしてあげる必要があります。
評価実験
本節では,前章で学習したz_dimが2,10,20の3つのモデルを用いて,各種定性評価実験を行います。具体的には,再構成画像の生成や潜在空間の可視化を丁寧に行っていきます。
再構成画像の定性評価
再構成画像に関する定性的な評価実験を行います。
# 評価対象のモデルをインスタンス化する
model_z_2 = VAE(2)
model_z_10 = VAE(10)
model_z_20 = VAE(20)
model_z_2.load_state_dict(torch.load("./z_2.pth"))
model_z_10.load_state_dict(torch.load("./z_10.pth"))
model_z_20.load_state_dict(torch.load("./z_20.pth"))
# forループを回すためにモデルをリスト化する
model_list = [model_z_2.eval(), model_z_10.eval(), model_z_20.eval()]
# 可視化開始
for num_batch, data in enumerate(dataloader_test):
fig, axes = plt.subplots(4, 10, figsize=(20, 4))
for i in range(axes.shape[0]):
for j in range(axes.shape[1]):
axes[i][j].set_xticks([])
axes[i][j].set_yticks([])
# まずは入力画像を描画
for i, im in enumerate(data[0].view(-1, 28, 28)[:10]):
axes[0][i].imshow(im, "gray")
# z_dim=2, z_dim=10, z_dim=20の3つの学習済みVAEについて再構成画像を描画
for i, model in enumerate(model_list):
_, _, y = model(data[0], device)
y = y.cpu().detach().numpy().reshape(-1, 28, 28)
for j, im in enumerate(y[:10]):
axes[i+1][j].imshow(im, "gray")
fig.savefig(f"./reconstruction_{num_batch}.png")
plt.close(fig)
潜在変数の次元数を上げた方がモデルの表現力が高まりますので,それだけ再構成画像もはっきりとしていることが分かります。一方で,z_dim=10とz_dim=20ではそこまで大きな差は見られませんでした。ここで注意が必要なのは,再構成が上手くできているからといって,ラベルの判別が正確に行われているという訳ではないという点です。潜在空間も綺麗にマッピングされているとは限りません。
潜在空間のマッピング
MNISTのテストデータを入力した場合に,潜在空間がどのようにマッピングされているのかを確認しましょう。分かりやすさのため,z_dim=2で学習したモデルを利用します。
z_dim = 2
model = VAE(z_dim)
cm = plt.get_cmap("tab10") # カラーマップの用意
# 可視化開始
for num_batch, data in enumerate(dataloader_test):
fig_plot, ax_plot = plt.subplots(figsize=(9, 9))
fig_scatter, ax_scatter = plt.subplots(figsize=(9, 9))
# 学習済みVAEに入力を与えたときの潜在変数を抽出
_, z, _ = model(data[0], device)
z = z.detach().numpy()
# 各クラスごとに可視化する
for k in range(10):
cluster_indexes = np.where(data[1].detach().numpy() == k)[0]
ax_plot.plot(z[cluster_indexes,0], z[cluster_indexes,1], "o", ms=4, color=cm(k))
fig_plot.savefig(f"./latent_space_z_{z_dim}_{num_batch}_plot.png")
fig_scatter.savefig(f"./latent_space_z_{z_dim}_{num_batch}_scatter.png")
plt.close(fig_plot)
plt.close(fig_scatter)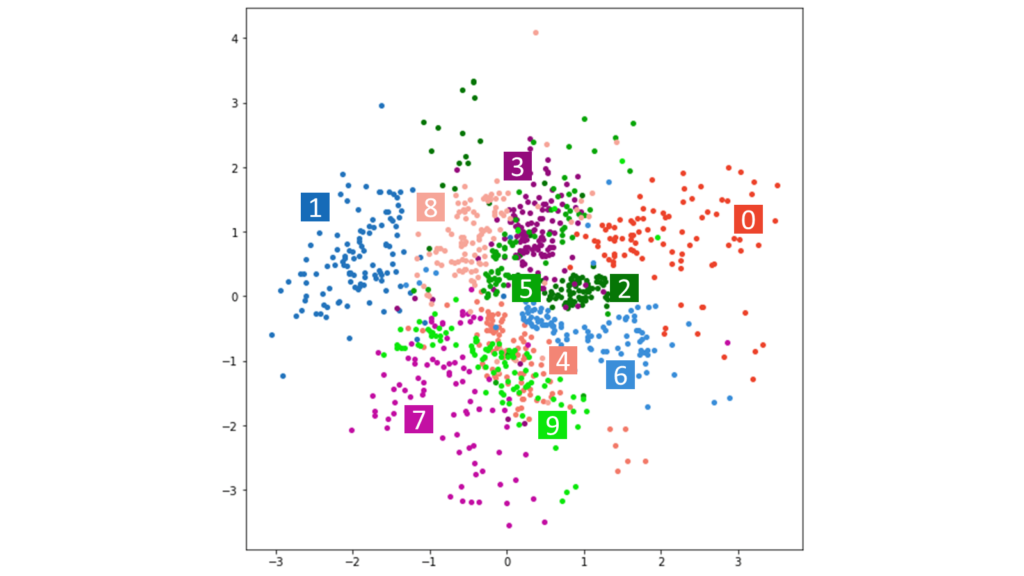

潜在変数の次元数が2の場合でも,比較的綺麗にマッピングされていることが分かりました。潜在変数の事前分布には標準正規分布を仮定していましたので,原点を中心としたマッピングになっています。
中央下部では4と9が混在していますが,これはMNISTにおいて4と9が似ていること,すなわち判別が難しいことを意味しています。潜在空間の次元数を上げれば,より多角的に手書き数字の特徴量を抽出することができますので,4と9を判別することができるようになります。実際,MNISTの最高精度は99%を越えています。
本稿でお見せしている画像は,当サイトの独自カラーリストを適用しています。実装例では,汎用性のためtab10のcolormapを利用していますが,本質的に大切な部分ではないため気にしなくて大丈夫です。また,潜在空間の次元数が2でない場合も,主成分分析やt-SNEを利用することで次元削減を行うことができ,2次元にマッピングすることが可能になります。
潜在変数を用いた再構成画像の生成
上ではテストデータを入力した場合の潜在空間のマッピングを確認しましたが,ここでは潜在変数を人工的に与えた場合の再構成画像を確認してみましょう。具体的には,以下の格子点を潜在変数とみなしてデコーダに入力してあげたときに,どのような画像が生成されるかを確認します。
l = 25 # 一辺の生成画像数
# 横軸と縦軸を設定して格子点を生成
x = np.linspace(-2, 2, l)
y = np.linspace(-2, 2, l)
z_x, z_y = np.meshgrid(x, y)
fig, ax = plt.subplots(1, 1, figsize=(9, 9))
ax.plot(z_x, z_y, "o", ms=4, color="k")
fig.savefig("lattice_point.png")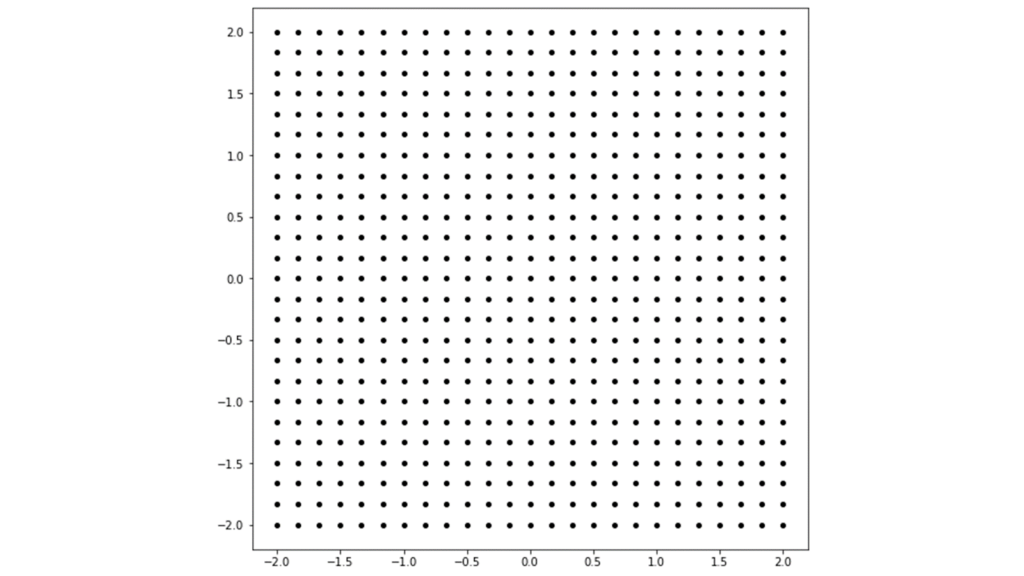
要するに,潜在変数において以下の範囲の格子点を人工的に利用するということです。
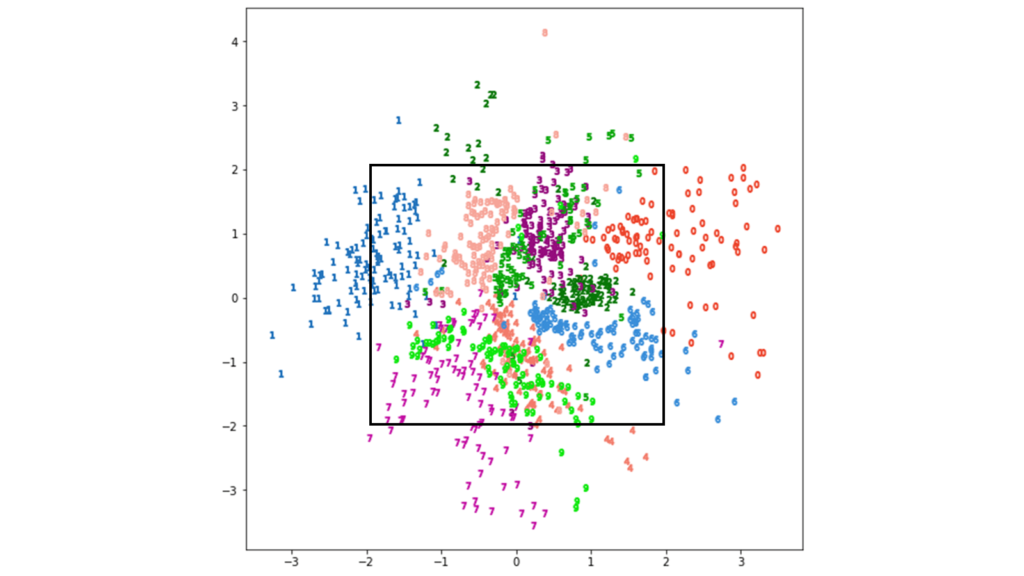
早速,格子点のデータをデコーダに入力してみましょう。
Z = torch.tensor(np.array([z_x, z_y]), dtype=torch.float).permute(1,2,0) # 格子点を結合して潜在変数とみなす
y = model_z_2.decoder(Z).cpu().detach().numpy().reshape(-1, 28, 28) # デコーダに潜在変数を入力
fig, axes = plt.subplots(l, l, figsize=(9, 9))
# 可視化開始
for i in range(l):
for j in range(l):
axes[i][j].set_xticks([])
axes[i][j].set_yticks([])
axes[i][j].imshow(y[l * (l - 1 - i) + j], "gray")
fig.subplots_adjust(wspace=0, hspace=0)
fig.savefig("from_lattice_point.png")
しっかりと,先ほど可視化した潜在変数のマッピングに準じた可視化結果となりました。潜在変数を人工的に作成していますので,デコーダの出力である再構成画像は実際にMNISTには存在しない画像になります。この実験は,潜在空間をいじることでVAEが様々な生成タスクで応用できる可能性を示唆しています。実際に,VAEを用いて音楽を生成するMusicVAEが考案されています。
潜在空間のウォークスルー
潜在空間を線形的に渡り歩いたときにどのように再構成画像が変化するのかをアニメーションで確認します。具体的には,以下の4方向を渡り歩いてみましょう。
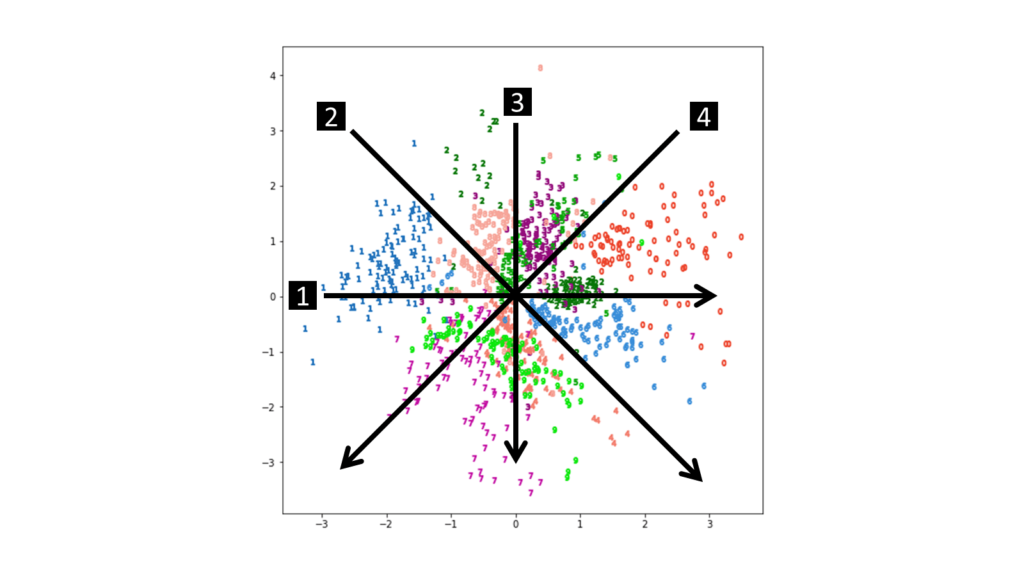
実際に,4つの方向で潜在変数を線形的に変化させながらデコーダに入力してみましょう。
from matplotlib.animation import ArtistAnimation # gif作成のためにmatplotlibのモジュールを利用
step = 50 # 何枚の画像アニメーションに用いるか
z_dim = 2 # 潜在変数は2
# 4つの方向のスタート地点とゴール地点を座標で定義
z11 = torch.tensor([-3, 0], dtype=torch.float)
z12 = torch.tensor([3, 0], dtype=torch.float)
z21 = torch.tensor([-3, 3], dtype=torch.float)
z22 = torch.tensor([3, -3], dtype=torch.float)
z31 = torch.tensor([0, 3], dtype=torch.float)
z32 = torch.tensor([0, -3], dtype=torch.float)
z41 = torch.tensor([3, 3], dtype=torch.float)
z42 = torch.tensor([-3, -3], dtype=torch.float)
# for文を回すためにリスト化する
z1_list = [z11, z21, z31, z41]
z2_list = [z12, z22, z32, z42]
# 線形変化させた潜在変数を格納するリスト
z1_to_z2_list = []
# デコーダの出力を格納するリスト
y1_to_y2_list = []
# 潜在変数のスタート地点からゴール地点を線形的に変化させてリストに格納する
for z1, z2 in zip(z1_list, z2_list):
z1_to_z2_list.append(torch.cat([((z1 * ((step - i) / step)) + (z2 * (i / step))) for i in range(step)]).reshape(step, z_dim))
# 各潜在変数をデコーダに入力したときの出力をリストに格納する
for z1_to_z2 in z1_to_z2_list:
y1_to_y2_list.append(model_z_2.decoder(z1_to_z2).cpu().detach().numpy().reshape(-1, 28, 28))
# gif化を行う
for n in range(len(y1_to_y2_list)):
fig, ax = plt.subplots(1, 1, figsize=(9,9))
fig.subplots_adjust(left=0, right=1, bottom=0, top=1)
ax.set_xticks([])
ax.set_yticks([])
images = []
for i, im in enumerate(y1_to_y2_list[n]):
images.append([ax.imshow(im, "gray")])
animation = ArtistAnimation(fig, images, interval=100, blit=True, repeat_delay=1000)
animation.save(f"linear_change_{n}.gif", writer="pillow")
潜在空間のマッピングに従って,徐々に再構成画像が変化していることが分かります。興味深いのは,数字が変化するスピードが4方向とも綺麗に揃っている点です。これは,潜在空間が原点を中心とする標準正規分布に従っていることが起因しています。どの方向とも,原点に向かってから離れていく方向に線形的に移動していますので,数字が変化するスピードも揃うという訳です。ただし,各数字の分布が縦長であったり横長であったりすると結果が変わってきます。確実に言えるのは,標準正規分布は原点に近いほど密度が濃いですので,ウォークスルーでも原点付近を通る区間では数字が変化するスピードが速まっているということです。
おわりに
本稿では,世間に流布している「VAEはオートエンコーダの発展手法だ」という誤解を正すために,EMアルゴリズムと変分ベイズの2つの観点からVAEを正確に捉え直しました。冒頭でもお伝えしたように,VAEはGANやFlowと並んだ三大巨頭として,近年の深層学習の隆盛を支えてきました。
更なる学習のためには,以下の論文を参考にするとよいでしょう。
- VAE[Kingma+, 2013] の主な流派
- Conditional VAE [Kingma+, 2014]
- β-VAE [Higgins+, 2017]
- GAN[Goodfellow+, 2014] の主な流派
- pix2pix [Isola+, 2017]
- CycleGAN [Zhu+, 2017]
- Progressive GAN [Karras+, 2018]
- StyleGAN [Kerras, 2019]
- Flow[Rezende+, 2015] の主な流派
- NICE [Dinh+, 2015]
- IAF [Kingma+, 2016]
- Real NVP [Dinh+, 2017]
- Neural ODE [Chen+, 2018]
[1] Kingma+, Auto-Encoding Variational Bayes. (ICLR 2014)
[2] Kingma+, Semi-Supervised Learning with Deep Generative Models. (NIPS 2014)
[3] Higgins+, beta-VAE: Learning Basic Visual Concepts with a Constrained Variational Framework. (ICLR Poster 2017)
[4] Dupont+, Joint-VAE: Learning Disentangled Joint Continuous and Discrete Representations. (arXiv 2018)
[5] Oord+, Neural Discrete Representation Learning. (NIPS 2017)
[6] Goodfellow+, Generative adversarial nets. (NIPS 2014)
[7] Isola+, Image-to-Image Translation with Conditional Adversarial Networks. (CVPR 2017)
[8] Karras+, Progressive Growing of GANs for Improved Quality, Stability, and Variation. (ICLR 2018)
[9] Karras+, A Style-Based Generator Architecture for Generative Adversarial Networks. (TPAMI 2021)
[10] Rezende+, Variational Inference with Normalizing Flows. (ICML 2015)
[11] Dinh+, NICE: Non-linear Independent Components Estimation. (ICLR Workshop 2015)
[12] Dinh+, Density estimation using Real NVP. (ICLR Poster 2017)
[13] Chen+, Neural Ordinary Differential Equations. (NIPS 2018)
[14] Kingma+, Improving Variational Inference with Inverse Autoregressive Flow. (arXiv 2016)


コメント
コメント一覧 (84件)
大変丁寧でわかりやすい解説ありがとうございます。
Beginaidの前記事から来た者です。
前記事の最後のコメントで、再構築誤差の実装にてtorch.meanではなくtorch.sumを使う理由について、torch.meanだとバッチ方向にも均してしまうからだとありました。
しかし本解説を拝読した限り、モンテカルロ近似に使うサンプルをL=1としており平均をとる必要がないところを、余分に次元数nで割ってしまうことになるからだと理解したのですが、正しいでしょうか?
バッチ方向に平均をとっているわけではないですよね?
古い記事の、しかもコメントに対する質問になってしまい申し訳ありません。
Pal様
ご質問ありがとうございます!
前のブログからの読者様ということで,非常に嬉しく思います。
>モンテカルロ近似に使うサンプルをL=1としており平均をとる必要がないところを、余分に次元数nで割ってしまうことになるからだと理解
おっしゃる通りです。
前回の記事では不正確な内容をお伝えしてしまい大変失礼致しました。
一点補足しておくと,バッチ方向に関してはmeanを使ってもsumを使っても問題はありません。
あくまでも次元数側でmeanを取る操作自体に問題がありますので,バッチ数側にmeanを取ってもsumを取ってもlossのオーダが変わるだけで,VAEの学習に対して本質的には寄与しません。
いつも参考にさせていただいております。
質問なのですが,(46),(47)式あたりのI次元単位分布はI次元単位行列のことでしょうか…?なにぶん勉強中の身ですのでもし勘違いでしたら申し訳ありません。MNISTの数字グリグリ変化させたくて勉強してます!
ご質問ありがとうございます!
$\mI$が$D$次元単位分布というのは誤植でした。正しくは,$D$次元単位行列です。
こちらで理解できそうでしょうか?
よく見たらIとDを書き間違えてました...!すみませんややこしくて...
ありがとうございます。おかげさまで大分理解できたように思います。
本当に丁寧で素晴らしい解説です。
ただ、『初心者』と言っても、ニーズが人それぞれで、私の場合『概念』、『仕組み』、『数学原理』に関する『丁寧』で『徹底的』な解説を一番ありがたく感じます。
『実装』に関して、世の中にサンプルコードが山山あります。
=================================
なので、元のドキュメント《【超初心者向け】VAEの分かりやすい説明とPyTorchの実装》は
自分にとって非常に貴重です。
★ さて、主に”元のドキュメント”(https://tips-memo.com/vae-pytorch#3p_theta)に関する質問ですけれども、
ご教授いただければ幸いです。
=================================
Q1:
式(1)の中の N(x; μφ, σφの平方) は N(z; μφ, σφの平方)の間違いでは?
///////////////////////////////////////////////////////////////////
Q2:
AutoEncoderの目的関数の構成からすれば、式(1)中の分布=式(2)の分布であるべき、、
即ち、良く訓練されたAutoEncoderのμφ= 0 vector , σφの平方= 単位matrix でしょうか。
///////////////////////////////////////////////////////////////////
Q3: 『大切なのは,デコーダpθに関する分布は自分たちで定める必要があるという点です。』と述べられていますが、
ここのpθは一体pθ(x)ですか、それともpθ(z) や pθ(x|z), pθ(x,z)でしょうか。
///////////////////////////////////////////////////////////////////
Q4:
pθ(x)は分布を表すのですか、それともAutoEncoderの【目的関数】ですか。
///////////////////////////////////////////////////////////////////
「 質問9:潜在変数は等式で生成されるのでしょうか
本来であればエンコーダが出力したパラメータを元にが自然に生成されるべきなのですが,本文中にもある通り「自然に生成される」というランダム操作を組み入れてしまうとニューラルネットワークの誤差伝播が途切れてしまいますので」
Q5:
「自然に生成される」という表現がよく出ましたが、意味が分かりません。
そして具体的に何を、どうやって「自然に生成される」のでしょうか。
Q6:
どうして「自然に生成される」と、「ニューラルネットワークの誤差伝播が途切れてしまいます」のでしょうか。
///////////////////////////////////////////////////////////////////
「 質問12:Decoderの出力分布がEncoderの入力分布を”忠実に”再現するように学習するってこと?」
Q7:
Pθ(x) 、または log(Pθ(x)) は『AutoEncoder』システムの【目的関数】ですか
それともPθ(x) はDecoderを表すのでしょうか。
またはPθ(x) はDecoderの出力分布を表すのでしょうか。
////////////////////////////////////////////////////////////////////
「 質問20:再構成データはどのようにして生成されるのか
本文中にあるVAEの図の1枚目のようにパラメータを出力する場合はサンプリングなどを利用します。」
Q8:
decoderが【(分布の)パラメータを出力する場合】は入力データがどのように再構成されるのでしょうか
////////////////////////////////////////////////////////////////////
《 超初心者向け】VAEの分かりやすい説明とPyTorchの実装》より
「 ああ!ギブスサンプリングとか使えばええんちゃう?
Nooooです。サンプリングを行ってしまうと,誤差を逆伝播することが不可能になってしまうからです。
ですから,zの値は決定的に定めなくてはなりません。そこで,編み出された妙案がこちらの式です。」
「つまり,分布を仮定してサンプリングするのではなく,zというのは平均値にノイズ項を加えたものですよと近似してしまうというアイディアです」
《【徹底解説】VAEをはじめからていねいに》より
「デコーダの受け付ける入力はZです。そこで,エンコーダの出力したパラメータに従う確率分布から,微分可能な形で潜在変数Zをサンプリングする必要が出てきます。
一般には,サンプリングという処理は微分不可能です。」
Q9:
ここに「サンプリング」とはどんな概念でしょうか。
Q10:
「Zをサンプリングする」とは具体的にどんな操作でしょうか。
Q11:
どうして「サンプリングという処理は微分不可能」のですか。
////////////////////////////////////////////////////////////////////
質問が多くて申し訳ございません。
複数回分けてご返答いただいても、幸いです。
川崎 紀泉 様
ご質問ありがとうございます。
一つずつお答えしていきますね。
Q1.
ご指摘ありがとうございます。誤植でしたので修正しました。
Q2.
はい。おっしゃる通りです。
Q3.
$p_{\theta}(Z)$と$p_{\theta}(X|Z)$です。
Q4.
$p_{\theta}(X)$は周辺尤度関数であり,確率分布を表します。$X$は観測データなので,$p_{\theta}(X)$は一定値になります。
Q5.
近似事後分布に基づいて潜在変数が生成されます。
Q6.
ランダム操作が介入するからです。決定的な処理で計算グラフが繋がっていない部分は微分不可能になり,誤差逆伝播を行うことができません。
Q7.
$p_{\theta}(X)$は真の周辺尤度関数です。Q4.でもお答えさせてもらいましたが,周辺尤度関数は一定値になりますので目的関数としては不適切です。詳しくは,【徹底解説】変分ベイズをはじめからていねいにをご参照ください。
Q8.
学習済みDecoderからのサンプリングなどが考えられます。例えば,Decoderにパラメータ$\lambda$を持つベルヌーイ分布を仮定する場合,ベルヌーイ分布の平均は$\lambda$となりますので,学習済みのDecoderのパラメータ$\lambda$そのものを代表点として採用することができます。
Q9.
サンプリングとは,確率分布から標本値を抽出する操作を表します。仮定した母集団から何か具体的な値を取り出すイメージです。
Q10.
近似事後分布$q_{\varphi}(Z|X)$から標本値$z$を抽出する操作を表します。
Q11.
Q6.でもお答えさせてもらった通り,ランダム操作が介入するからです。決定的な処理で計算グラフが繋がっていない部分は微分不可能になり,誤差逆伝播を行うことができません。
以上,ご確認お願い致します。
早速ご返信ありがとうございます。
ご説明を更に勉強したいと思います。
そして世の中確かに実装サンプルコードが多いけれども、新版中の実装ほどしっかりした解説を見たことはありません。
本当に素晴らしいです!
============================================
さて、
新版中の式(46),(47),(62),(63) に関する疑問ですけれども、言い間違ったら是非ご指摘頂きたいと思います。
分散値を対角にするのはvectorの『Covariance matrix』の場合だと思われます。
それにvectorのentriesに表される諸dimensionの間が直交である場合、『Covariance matrix』が対角matrixになります。
ところが、VAEで求めたいのは諸 Z vector集団の分布中心と分散のペアであり、Z vectorに関する『Covariance matrix』ではないので、
『Covariance matrix』の存在はナンセンスではと思います。
また、実装コードから分かるように、σφの平方(の対数)はz_dimのvectorとして生成されるので、
右にmatrix乗けられるのは横vectorしかありません。
仮にEncoderによって生成したのはz_dim次元のσφの平方(の対数)の『横vector』とします。
すると、右に単位matrix I を乗ける場合、結果は他ならぬ、z_dim次元のσφの平方(の対数)の『横vector』そのものです。
なので、概念的にも、数学的にもσφの平方に右掛け単位matrixはナンセンだと思います。
またどうぞよろしくお願い致します。
すみません!
=================
検証データ:12000枚
テストデータ:10000枚
=================
《検証データ》と《テストデータ》、それぞれどんな場合に利用されるのでしょうか。
特に《検証データ》に関して。
川崎 紀泉様
ご質問ありがとうございます。
>『Covariance matrix』の存在はナンセンス
分散共分散行列を用いるのは,ベクトルと行列で数式を表した方が簡潔に議論できるからです。おっしゃる通り,潜在変数の事前分布やデコーダの分散共分散行列が対角行列の場合には,各サンプルが独立と仮定していることが分かります。
>概念的にも、数学的にも$\sigma_{\varphi}$の平方に右掛け単位matrixはナンセンだと思います。
いえ,概念的にも数学的にも妥当です。本文中のどちらの式番号に対応するか明記いただけますか?
>《検証データ》と《テストデータ》、それぞれどんな場合に利用されるのでしょうか。
検証データは過学習を防ぐために利用されるデータです。テストデータはモデルの評価に利用されるデータです。学習時にはテストデータは決して触ってはなりませんので,「学習時に利用できる評価用のデータ」という意味合いで検証データが用いられます。本記事では,検証データの損失を元にearly stoppingを適用しています。検証データの扱いについては機械学習の基本中の基本になりますので,恐れ入りますがPRML等をご参照下さい。
丁寧なご説明ありがとうございます。
ごめんなさい、頭が可笑しかったんで、概念的に『Covariance matrix』でvectorの分散を表現するのは当たり前ですね!
ご指摘本当にありがとうございます。
ただ、ご自身の実装コードから分かるように、
////////////////////////////////////////////////////////////////////////
コンストラクタ
20 self.enc_fc3_logvar = nn.Linear(200, z_dim) # 近似事後分布の分散の対数
////////////////////////////////////////////////////////////////////////
σφの平方(の対数)はz_dimのvectorとして生成されるので、右にmatrix乗けられるのは横vectorしかありません。
仮にEncoderによって生成したのはz_dim次元のσφの平方(の対数)の『横vector』とします。
すると、右に単位matrix I を乗ける場合、結果は他ならぬ、z_dim次元のσφの平方(の対数)の『横vector』そのものです。
★即ち、対角型の『Covariance matrix』にならないのです。
============================================
> 学習時にはテストデータは決して触ってはなりませんので,「学習時に利用できる評価用のデータ」という意味合いで検証データが用いられます。
なるほど!
またよろしくお願いします
川崎 紀泉様
ご連絡ありがとうございます。
恐れ入りますが、質問の意図を汲み取ることができませんでした。本文中のどちらの式番号に対応するか明記いただけますか?
始めまして 金井と申します。
詳細なコメントのお陰でほとんどのコードが理解できましたが、
下記の文は僕にとって非常に難解で、ご説明いただけませんか。
optimizer = optim.Adam(model.parameters(), lr=0.001)
例えば、
model.parameters()はどんな内容の物でしょうか。
lr=0.001は?
名前からの推測ですけれども、もしかして、NNの『back propagation/ 誤差逆伝播』というやつは全部この文で実現するのでしょうか。
金井様
ご質問ありがとうございます。
> model.parameters()はどんな内容の物でしょうか。
こちらのドキュメントにもある通り、モデルのパラメータをイテレータとして返します。誤差逆伝播を行なっている訳ではありません。
> lr=0.001は?
こちらのドキュメントにもある通り、optimizerに渡す引数の一つです。学習率を表します。
また
順伝播処理:
KL = 0.5 * torch.sum(1 + log_var - mean**2 - torch.exp(log_var)) # KLダイバージェンス計算
について
式(73)に由来するかと思いますが、式(73)には「mean**2」がないようですけれども?
金井様
ご指摘ありがとうございます。
恐れ入りますが、式(73)においてmeanが二乗になっていないのは誤植になります。
近日中に修正を行いますので、少々お待ち下さい。
金井様
ご対応遅くなりましたが,本文中の誤植を修正しました。
この度はご指摘誠にありがとうございました。
> 恐れ入りますが、質問の意図を汲み取ることができませんでした。本文中のどちらの式番号に対応するか明記いただけますか?
説明不足で大変申し訳ございません!
新版中の式(47),(63),(64)の中のZ vectorの『Covariance matrix』に関する数学表現:
【σφの平方(の対数)に右にmatrix I を掛ける 】に疑問です。
数学的に右にmatrix乗けられるvectorは横vectorしかありません。
ご自身の実装コードから分かるように、
////////////////////////////////////////////////////////////////////////
コンストラクタ
20 self.enc_fc3_logvar = nn.Linear(200, z_dim) # 近似事後分布の分散の対数
////////////////////////////////////////////////////////////////////////
σφの平方(の対数)はz_dimのvectorとしてEncoderに生成されたので、仮に『横vector』だとします。
すると、右に単位matrix I を乗ける場合、結果は他ならぬ、z_dim次元のσφの平方(の対数)の『横vector』そのものです。
★即ち、対角型の『Covariance matrix』にならないのです。
================================================
ついでに、
式(61),(64)の中の記号|・|で表される計算は具体的にどんな計算でしょうか。
ノルムですか?
川崎 紀泉様
ご質問の意図が汲み取れました。
$\vsigma^2_{\varphi}$を太字でベクトルとしているのは誤植でした。
こちらスカラーに修正しましたのでご確認お願い致します。
>式(61),(64)の中の記号|・|で表される計算は具体的にどんな計算でしょうか。
行列式になります。こちらも注釈を書き逃していたため,「ただし,$|\cdot|$は行列式を表す。」という文章を式(61)の直後に挿入しました。
zuka 様
早速のご返答ありがとうございます。
前版も含め非常に素晴らしいドキュメントなので、心より感謝いたします。
> σφの平方を太字でベクトルとしているのは誤植でした。
> こちらスカラーに修正しましたのでご確認お願い致します。
これは大きな間違いでは?!
スカラー右掛け単位matrixの場合、対角同値のmatrixが生成され、要はEncoderによってσφの平方の対数のvectorを生成する意味がなくなりますよね。一つのσφの平方の対数だけ(i.e, スカラー)生成すれば済ませます。
しかし、現実に、確率変数Z vectorの各次元においての分散がいつも『同値』であるのはあり得ないのです。
言い間違ったら、ご指摘いただきたいと思います。
また宜しくお願い致します。
川崎 紀泉様
ご指摘ありがとうございます。
新しく分散共分散行列を定義し直して本文を修正いたしました。
式(47)以降のご確認をお願い致します。
お返答ありがとうございます
良い勉強になりました。
お陰様で、コードの学習は少しずつ進んできました。
真に申し訳ございませんが、また質問させていただきます。
《学習イテレーション》
////////////////////////////////////////////////////////
# 学習開始
................
for x, t in dataloader_train: # dataloaderから訓練データを抽出する
lower_bound, _, _ = model(x, device) # VAEにデータを流し込む
loss = -sum(lower_bound) # lossは負の下限
model.zero_grad() # 訓練時のpytorchのお作法
loss.backward()
optimizer.step()
////////////////////////////////////////////////////////
1.上記コードの中に『for x, t...』によって1回の取り出した訓練データはbatch分ですか、或いは一つの訓練データですか。
2. loss変数はどうして.backward()メソッドを持つのでしょうか。
初心者の感覚ですけれども、この.backward()こそ、NNのあらゆるparameterのgradが更新してくれる(Back-propagation)のですね?
3.上記コードで一つのbatch(mini-batch)単位でのNN parametersの更新を完成するのでしょうか。
どうぞよろしくお願いいたします。
金井様
ご質問ありがとうございます。
Q1.
batch分です。
Q2.
Pytorchがそのような設計をしているからです。backwardメソッドがどのような処理を表すのかは,ソースコードを参照ください。
Q3.
for文が完了したところで,訓練データに対する1epoch分の更新が行われます。ちなみに,各batchに対する更新は主に1stepと呼ばれています。
zuka 様
ご教授ありがとうございます。
ご説明のためにソースコードが断片化されてるのはやむを得ない事だと思いますが、
勉強するために、ソースファイルの形でまとめたものがほしいです。(コンパイルできるような形)
お願いできますでしょうか。
金井様
ご質問ありがとうございます。
こちらのリポジトリにソースコード一式をまとめています。
お世話になっております。
式(44),(46),(50)についてですけれども、
P(Z)はprior確率として予め標準正規分布に指定されている以上、decoderのparametersθに依存するはずはないので、Pθ(Z)で表現されるのは誤解されやすいのでは?
ちなみに、式(50)のKLの書き方にミスがありました("|" を "||"に )
言い間違ったら、ご指摘お願いいたします。
川崎 紀泉様
クリティカルなご指摘誠にありがとうございます!
どちらも修正させていただきました。
まとめられたソースファイルを拝見いたしました。
分かりやすいコメントのお陰で、大分分かるようになりました。
ただ、ソースコードというより幾つか隠れているようなものがまだはっきりしていません。
自分なりに調べてみたけれども、結果を得られませんでした。
例えば、
「 model.parameters()」の「parameters」って、NNの重み(=フィルター係数)の事でしょうか。
それから《学習イテレーション》に関して
////////////////////////////////////////////////////////
# 学習開始
................
for x, t in dataloader_train: # dataloaderから訓練データを抽出する
lower_bound, _, _ = model(x, device) # VAEにデータを流し込む
loss = -sum(lower_bound) # lossは負の下限
model.zero_grad() # 訓練時のpytorchのお作法
loss.backward()
optimizer.step()
////////////////////////////////////////////////////////
model(x, device) に代入したxがbatchであれば、xを引き受けたnn.Linearメソッドもbatch単位で実行しなければならないですね。
ところが、NNのforward計算は原理的に画像一枚ずつに対して行うわけで、同時に複数の画像(batch)を入力できないはず。。。
Pytorchのnn.Linearに関するドキュメントを調べても、この辺の仕組みが解明できませんでした。
自分の想像では、どっかにloopを設けて、batch中の画像を一枚一枚学習していくかな。。。
zuka様のご見解を伺いたいのです。
どうぞよろしくお願い致します。
金井様
ご質問ありがとうございます。
>「parameters」って、NNの重み(=フィルター係数)の事でしょうか。
基本的には重みを表します。ただし,parametersの役割はmodelにどのようなネットワークを用いているかに依存します。例えば,CNNとRNNではparametersの果たす役割が異なってきます。
>同時に複数の画像(batch)を入力できないはず
基本的に,バッチ処理は並列処理ですので,バッチに含まれるデータ分順伝播を同時に実行し,それらからある一つの損失を代表値として採用し(例えば平均・総和など),逆伝播を実行するという流れです。御幣を恐れずに言うならば,単一処理をベクトル演算とすると,バッチ処理は行列演算になります。すなわち,バッチ処理というのは,複数のベクトル(=単一処理)をひとまとまりにした塊(行列)同士の演算を実行し,ある単一の損失を計算し,逆伝播によって新しいパラメータの更新を行うという処理を意味します。forループは直列処理になりますので,バッチ処理の理解としては不適切です。バッチ処理は直列ではなく並列に計算できることが最大の利点です。一方で,直列処理とは異なり,並列処理の大きさに応じて(大量の)メモリを必要とするという欠点があります。
zuka 様
「parameters」の意味とTensorによるバッチ処理の天然性(必然性)に関するご解説ありがとうございました❣
ここのページにお出会いできて本当によかったです。
AI分野での益々のご活躍を期待しております。
お陰様で、reparameterize, 即ちlatent変数zの生成原理は分かりました❣
zukaさまご本人の実装コードも分かりやすかったのです。
感謝の気持ちいっぱいですね。
=====================================================
# zukaさまご本人の実装コードより
epsilon = torch.randn(mean.shape, device=device)
# ↑torch.randn : 平均が 0 で, 分散が 1 の正規分布(=標準正規分布)から乱数で満たされたテンソルを返す。
return mean + epsilon * torch.exp(0.5 * log_var)
=====================================================
ところが、ネット上にある幾つかの実装例からすれば、
epsilonの生成はEncoderの出力:std(=σ)に依存させているのに不思議に思います。
典型なzの生成法として、
例1:
self.mu = self.fc21(x)
self.logvar = self.fc22(x)
std = torch.exp(0.5*self.logvar)
eps = torch.randn_like(std) # Encoderの出力std(=σ)に依存させています❓
if self.training:
x = self.mu + std*eps
else:
x = self.mu
=====================================================
例2:
device = mu.device
std = torch.exp(0.5 * logvar) # = exp(0.5log(σ2))=σ
eps = torch.randn_like(std).to(device) # epsは分散为σのランダム変数ではないでしょ❓❣
return mu + eps * std
=====================================================
例3: 有名な《IntroVAE》の発明者自身の実装
def reparameterize (self, mu, logvar): # IntroVAEの実装
std = logvar.mul(0.5).exp_()
eps = torch.cuda.FloatTensor(std.size()).normal_()
eps = Variable(eps)
return eps.mul(std).add_(mu)
これはもっともちんぷんかんぷんの実装ですね
epsはまったくN(0,I)と関係の生成法ではないか❓ (泣く)
=====================================================
大変申し訳ございませんが、
このフィールドのマスターのzukaさまからヒントでも頂ければ助かります。
川崎様
ご質問ありがとうございます。
解答としてはシンプルで,torch.randn_likeは引数に渡されたテンソルの「サイズ」の情報しか利用しないからです。
torch.randn_likeのドキュメントを見ると,
>input (Tensor) – the size of input will determine size of the output tensor.
という記述があります。したがって,例えばtorch.randn_like(std)というのはstdと同じサイズのテンソルを標準正規分布から生成するという処理を行います。
お世話になっております。
誤差関数の出力 (Tensorオブジェクト) のbackwardメソッドは何故勾配の累積をするのでしょうか。
一説ではmini-batch訓練をサポートするためだそうですが、
zuka様の実装からも分かるようにmini-batch訓練の場合、tensor objectを利用すれば、
mini-batch単位の目標関数の誤差累積を簡単に求められるので、
目標関数の誤差累積に対するback propagationによって、NNパラメーターの更新ができるわけで、
NNの各パラメーターの勾配に対する累積の必要性は毛頭ありません。
勾配の累積の必要性がないので、毎回毎回『model.zero_grad()』や『NNParameters.zero_grad()』のような文を
loss.backward()とoptimizer.step()の直前に実行しなければなりません。
面倒の上非能率ですね。
一体どんな場合勾配の累積が必要になるのでしょうか。
zuka様のアイディアをお伺いさせていただきたいと思います。
どうぞよろしくお願いいたします。
川崎 紀泉 様
ご質問ありがとうございます。
pytorchが勾配を蓄積する理由ですが,正直なところ自分もよく理解できていません。
完全な推測にはなりますが,以下の三点が考えられます。
1. RNNに代表されるような時系列モデルで過去の勾配を利用するため
2. 勾配降下法の最適化アルゴリズムの中には過去の勾配を利用するものがあるため
3. メモリの省力化
お返答ありがとうございます。
>1. RNNに代表されるような時系列モデルで過去の勾配を利用するため
>2. 勾配降下法の最適化アルゴリズムの中には過去の勾配を利用するものがあるため
>3. メモリの省力化
そうですか、良い勉強になりました。
でも多くのDNN実装サンプルからすれば、勾配を蓄積(累算)したら困るんで、毎回zero_grad()を入れないと偉いエラーを引き起こされちゃうんですね。
それにzero_grad()を入れなかった事に気づきにくいのです。
当然zero_grad()実行分の能率も悪くなります。
ごめんなさい、個人感想ですけれども、『勾配の蓄積』が必要となる場合のためのスイッチ設定を用意して、必要の時だけ利用すれば良いかな、、、
川崎 さま
勾配に関する操作はライブラリ側でラップしておきたいという思想なのだと思います。
デフォルトで勾配蓄積する仕様の理由は分かりかねますが,
>勾配を蓄積(累算)したら困る
と感じられるのは,いわゆる古典的なモデルの実装をしているからではないでしょうか。
より複雑なアーキテクチャのモデルを実装する際に,ありがたみを感じられるのかもしれません。
>『勾配の蓄積』が必要となる場合のためのスイッチ設定を用意してくれて、必要の時だけ利用すれば良いのに、、、
Pytorchの開発チームに言いたいのです。
とても分かりやすい記事をありがとうございます!!
VAEに関しての理解が浅い自分にとって、とても役立つ記事でした!
さて、一つ質問なのですが、$p_{\theta}(z)$と$q_{\phi}(z|x)$の分布を近づけるように学習し、$p_{\theta}(z)$が$\N(z,0;I)$だと仮定するということは、学習を進めると$q_{\phi}(z|x)$の平均は0に、分散は1に近づくのでしょうか?
仮にそうだとすると、$q_{\phi}(z|x)$が近づくべき値は自明なので、学習の意味がないと思ってしまいました、、、
頓珍漢な質問であったら申し訳ありません。
江口 さま
ご質問ありがとうございます!
>$p_{\theta}(z)$が$\N(z,0;I)$だと仮定するということは、学習を進めると$q_{\phi}(z|x)$の平均は0に、分散は1に近づくのでしょうか?
はい,近づきます。本稿の「評価実験>潜在空間のマッピング」の節で,潜在空間が平均0,分散1の分布となっていることを定性的に確認できます。ただし,学習の仕方によっては事前分布による正則化よりも再構成誤差の寄与の方が大きくなり,$q_{\phi}(z|x)$が標準正規分布に近づかないケースもあります。
>$q_{\phi}(z|x)$が近づくべき値は自明なので、学習の意味がないと思ってしまいました
なるほど。恐れ入りますが,「$q_{\phi}(z|x)$が近づくべき値は自明」という部分が理解できませんでした。下限にKLダイバージェンスによる正則化項を入れないと,$q_{\phi}(z|x)$は自由に動いてしまいますので,必ずしも標準正規分布に近づくとは限らないです。私が質問の意図をうまく汲み取れていない可能性が高いため,少し補足していただけますとクリティカルな回答が可能かと思われます。
丁寧なご回答、本当にありがとうございます!
平均が0に、分散が1に近づく場合は、$q_{\phi}(z|x)$が必ず標準正規分布に近づいてしまうと勘違いしていました!
また、$q_{\phi}(z|x)$がある値に近づくように学習する過程でパラメータが調整されることに意味があるので、「$q_{\phi}(z|x)$が近づくべき値が自明であると、学習に意味はない」というのもおかしな話でした(笑)
このような素晴らしいコンテンツが揃ったメディアがあることに感謝しています!
今後も応援しています!
質問に答えてくださり、ありがとうございました!!
いえいえ,こちらこそ参考にしていただけて嬉しいです!
今後とも何卒よろしくお願い致します。
解説ばかりでなく、実装も超素晴らしいですね。
質問として、潜在変数(z)の各次元上の数値範囲を予め見積もる方法はあるのでしょうか。
例えば、walkthroughメソッド実装の際、どうやって2次元のlatent 変数の二つのdimにおいてのデータ範囲は皆[-3, 3]内に集中しているのを分かっているのでしょうか?
=============コード引用==============
z11 = torch.tensor([-3, 0], dtype=torch.float)
z12 = torch.tensor([3, 0], dtype=torch.float)
z21 = torch.tensor([-3, 3], dtype=torch.float)
z22 = torch.tensor([3, -3], dtype=torch.float)
z31 = torch.tensor([0, 3], dtype=torch.float)
z32 = torch.tensor([0, -3], dtype=torch.float)
z41 = torch.tensor([3, 3], dtype=torch.float)
z42 = torch.tensor([-3, -3], dtype=torch.float)
z1_list = [z11, z21, z31, z41]
z2_list = [z12, z22, z32, z42]
=================================
これは見事ですね!
アイディアを教えてくださいませんか。
Dijkstra 様
ご質問ありがとうございます。
お褒めの言葉も嬉しい限りです。
>潜在変数(z)の各次元上の数値範囲を予め見積もる方法はあるのでしょうか。
ありません,というのが回答になります。というのも,潜在変数の近似事後分布はあくまでも「確率分布」ですので,定義域が実数全体をとるときには,潜在変数が必ずどこか特定の範囲に現れるという保証はないからです(本稿でも近似事後分布として正規分布を仮定していますので,計算機的な限界を無視すれば,とりうる定義域は実数全体です)。ただし,十分学習された近似事後分布であれば,分散は比較的小さな値(本稿の場合は$1$)に近づいているはずですので,正規分布の簡単な計算により大雑把に予測を行うことは可能です。一方,本稿のwalkthroughでは,潜在変数を人工的に作り出していますので,理論的には潜在変数としてどのような座標を用いてもOKです。極端ですが,$[-100,100]$のような潜在変数をデコーダに突っ込むこともできます。しかしながら,近似事後分布は平均$0$,分散$1$に近づいているはずですので,$[-100,100]$のような座標には潜在変数はマッピングされておらず,意味のある出力にはなりにくいだろうと予想できます。
>どうやって2次元のlatent 変数の二つのdimにおいてのデータ範囲は皆[-3, 3]内に集中しているのを分かっているのでしょうか?
$[-3, 3]$は決め打ちです。おそらく,学習データから抽出された潜在変数は$(-\infty,-3)$と$(3,\infty)$にもマッピングされているはずですが,$[-3,3]$くらいの範囲で人工的に潜在変数を作ってあげれば,潜在変数の性質を定性的に確認できるだろうという経験則に基づき判断しました。
お久しぶりです。
下記3点についてご教授いただければ幸いです。
1.ご紹介頂いたKL-Dに関して、最小値は0であるのは分かりましたが、KL-Dの上限値は何でしょうか。
2.多次元確率変数の場合、具体に、Encoderの出力の分布と標準正規分布の間のKL-Dに関して、直感的に次元が高いほどKL-Dの値も高くなります。これはご提供のAVEコードの実行で検証しました。
さて、KL-Dの値域を確率変数zの次元数に依存しないように変更できるのでしょうか。
3.KL-Dの値域とVAEの入出力X,Yの間クロスエントロピーの値の範囲が10倍上も100倍以上もの差があって、KL-Dが誤差量としてほぼ埋没されています。
この2種類異なる種類の誤差をそのまま足して誤差としてNNの訓練に利用されるのは荒いと感じざるを得ません。改善や回避する方法はないでしょうか。
よろしくお願い致します。
川崎さま
ご質問ありがとうございます。
1. KLダイバージェンスの値域
KLダイバージェンスは乖離度の指標の一つですので,値域は$[0, \infty)$となります。KLダイバージェンスが非負の値をとり,Forward KLもReverse KLもlogの重み付け和であることに注意すると,値域が$[0, \infty)$となることは理解できると思います。
2. KLダイバージェンスのスケール
潜在変数に依存する変数で標準化を行うことでスケール調整することが可能です。最も単純には,潜在変数の次元数で割るといった方法が考えられます。
3. KLダイバージェンスとReconstructionのスケール
これは多くの研究が進んでいるトピックです。結論から言えば,必ずしもKLダイバージェンスとReconstructionのスケールが揃っていた方が学習がスムーズに進むとは限りません。どのような重み付けを行うべきかに関しては,私の知る限りでは結論が出ていないというのが現状だと思います。
Reconstructionを学習するよりも先にKLダイバージェンスが最小化されることにより,事後分布が事前分布と一致してしまい事後分布の表現力が落ちてしまうことをPosterior collapseとよびます。学習初期には再構成誤差よりもKLダイバージェンスの方が優先されて学習される [Bowman+, 2016]ことにより,VAEの学習がうまく進まないこともあります。Posterior collapseを防ぐためには,KLダイバージェンスによる正則化項の重みを徐々にあげていくwarm upなどが用いられます。他にも,Cyclical Annealing Schedule [Fu+, 2019]なる手法も提案されています。また,VAEの最もベーシックな派生の一つのbeta-VAEは,KLダイバージェンスによる正則化項の重み付けを行っています。
このように,KLダイバージェンスとReconstructionのスケールに関してはさまざまな研究が進んでおりますので,論文をサーベイしていただけると新たな知見が得られるかと思います。
ZUKAさま
いつもお世話になっております。色々良い勉強になりますた。
自分も『独自』の幾つかのtraining パターンで訓練効果を試しました。
例えば、訓練を分割:
KL-DをEncoder-NNに対する訓練用で、「再構成誤差」をDecoder-NNの訓練に用います。要はVAE全体に対する一括訓練以外、VAEを部分的に単独訓練を実施したり、あるいはその上、更に「画像再構成誤差」に関する総体訓練も試したりします。
【結果】
KL-Dを完全に無視して、訓練しないほうは、VAEの再構成誤差が小さくなります。
間違った再構成画像の数も小さくなります。
【推測理由】
そもそもEncoderの出力の全体を標準正規分布に近づかせるのはあくまで付加価値を追求したいようなもので、画像再構成精度の追求に相反します。
個人的な想像ですけれども、非常にバラエティーな入力画像を精確に再現するために、Encoderの出力に「くびれ(次元縮小)」以外に余計な条件に強引に束縛されるほど、画像再構成の精度に悪い影響でしょう。
画像再現錯誤や精度の立場(これこそ実用化にもっとも重要な問題)から、KL-DでEncoderの出力分布を標準正規化にしようとする意味について私はうまく理解できません。
これに関しても、ZUKAさまよりアイディアをいただければ幸いですね。
ご多忙にもかかわらず、本当にありがとうございました!!!
川崎様
ご質問ありがとうございます。
VAEはオートエンコーダとはそもそもの思想が異なります。すなわち,(画像の)再構成を行うことが目的ではありません。あくまでも変分推論をDNNの文脈で用いて近似事後分布を求めることが目的です。したがって,VAEの精度を再構成誤差だけで評価するのは適切ではありません。
また,実験は学習データ・検証データ・テストデータに分割して行いましたでしょうか。学習データのみで評価している場合,過学習している恐れがあります。
> あくまで付加価値を追求したいようなもの
半分正解で,半分間違いです。「VAEはオートエンコーダの発展系だ」という理解をしていると,このような誤解をしてしまうことがあります。本文中でも申し上げておりますが,VAEの目的は事後分布を近似することであり,画像を再構成することではありません。あくまでも,変分推論における下限の文脈でKLダイバージェンスが出現します。「下限における正則化項」という意味で付加価値という言葉を使われているのであれば,理解は正しいです。変分推論は,事前分布の設定方法によってMAP推定にも最尤推定にもなり得るからです。一方で,オートエンコーダの目的関数と比較した「付加価値」という意味で使われているのであれば,理解は不適切だと思います。
> 画像再現錯誤や精度の立場(これこそ実用化にもっとも重要な問題)
上述の通り,「画像をどれだけ正確に再構成するか」よりも,汎化性能の方が実用化にもっとも重要な問題です。
> KL-DでEncoderの出力分布を標準正規化にしようとする意味
上述の通り,変分推論における下限を分解したときに出現する項です。"context"を考慮して事後分布を近似するために用いられる正則化項です。
お返事本当にありがとうございます。
良い勉強になりました。
>「VAEはオートエンコーダの発展系だ」という理解をしていると,このような誤解をしてしまうことがあります
まったくご指摘の通り、自分はVAEをそのようなものとして理解してしまいました。
《汎化性能》: 認識系のアプリケーションにとって命ですね。
よく分かりました。
《現時点の自分の認識》:
VAEの訓練結果として、訓練データに現れる頻度の高い画像サンプルほど、それが対応するKL-Dの値が低い➡正規分布に近くなりました。
★ なので、テスト段階で某入力画像に対するEncoder出力のKL-Dの大きさをその画像に異変があったかどうか判定の目安として利用したいのですが、理論的に信用できるのでしょうか。
=====
誤植と思いますが、《変文推論》➡ 《変分推論》
川崎さま
ご質問,誤植のご指摘ありがとうございます。
>Encoder出力のKL-Dの大きさをその画像に異変があったかどうか判定の目安として利用したい
「画像の異変」の定義次第です。たしかに,学習データに含まれないような特徴を示すデータが汎化性能の低いモデルに入力された場合には,潜在空間の確率密度が低い場所に潜在変数がマッピングされる可能性はあります。
VAEを用いた異常検知の手法は数多く発表されているはずですので,一度サーベイしていただけると知見が得られるかと存じます。キーワードとしては,"Anomaly Detection"と"VAE"です。
zuka様
いつも拝見させていただいております。
独学で知識が浅く、的外れかもしれませんが質問させてください。
Q1:VAE(事前分布に標準正規分布)のエンコーダで得られる平均と分散の値は、それぞれ1つずつの値であるという解釈でよろしいでしょうか?
※言い換えると、「平均の値が2つ以上&分散の値が2つ以上で計4つ以上の値が求まる」ではなく、単純に「平均の値が1つ&分散の値が1つで計2つの値しか求まらない」という解釈で良いかという質問です。
Q2:Q1に関連しますがMNISTを例にとる場合、エンコーダにて「0の分布の平均と分散」、「1の分散の平均と分散」が別々に求まっている訳ではないという解釈で合っていますか?
Q3:潜在空間に多峰性を仮定する場合はどのような手法が取られているのでしょうか?
VAEで可能であればその手法について教えていただけますでしょうか。また、VAEと組み合わせたりそれ以外の手法でもあればそれも教えていただきたいです。
※例えばMNISTだと、「0の分布の平均と分散」と「1の分散の平均と分散」...「9の分散の平均と分散」をそれぞれ求めたいし、それを同じ潜在空間にマッピングしたい場合です。
初心者さま
ご質問ありがとうございます。
一つずつお答えしていきますね。
Q1:
平均と分散はそれぞれ一つずつの値で合っています。ただし,バッチ学習を行う場合には,各ミニバッチごとに一つの平均と分散が出力されます。
Q2:
本記事で紹介している素朴なVAEでは,あるデータセットに対してエンコーダは一つになります。なぜなら,我々が求めたいのは近似事後分布だからです。各数字に対応するエンコーダをそれぞれ独立に学習している訳ではなく,一つのエンコーダである近似事後分布を学習します。
Q3:
潜在空間に多峰性を仮定する場合,大きく3つの方法が考えられます。
1. シンプルに多峰性の分布を事前分布に仮定する
→ 事前に潜在変数のクラスタ数を知る必要があることに加え,解析的な解を求めることが難しい場合が多いため,あまり利用されない印象があります。
2. 潜在空間のDisentangleを行う
→ 近年非常にホットな研究分野です。潜在空間でcontext(MNISTの場合は各数字)が綺麗に分離されるように様々な工夫を施します。"VAE Disentangle"でサーベイしていただければ数多くの手法が検討されていることを知ることができます。
3. 距離学習を導入する
→ 2.と関連して距離学習なるものが利用されることがあります。これは潜在空間を識別モデルとして利用したい場合によく用いられる手法です。MNISTでいえば,各数字のクラスタがそれぞれ綺麗に分離するように損失関数を設定するといったイメージです。距離学習は,VAEに限らず幅広く利用される汎用的な概念です。
zuka 様
これほど素晴らしいページを拝見できるのは私にとってラッキーの気持ちいっぱいです。
まず心より感謝したいと思います。
さて、超難問ですけれども、KL≧0 でなければならないので、式(62)≧0 である事を如何に証明するのでしょうか。
ここの主題から外れて申し訳ございませんが、関連している重要な数学問題として、
提起しておきたいのです。
ともりさま
ご質問ありがとうございます。ともり様の意図としては,式($\ref{eq_KL_gaussian}$)の右辺が非負であることを知りたいとのことでしょうか。そうであれば,論理構造が逆だというのが私の意見です。
「KLダイバージェンスが非負でなくてはならない」ではなく,「一般にKLダイバージェンスはどのような$p.q$に対しても非負となる」のです。ゆえに,KLダイバージェンスの性質から式($\ref{eq_KL_gaussian}$)の右辺が非負であることが導かれます。いかがでしょうか。
お返答ありがとうございます❣
説明不足で御免なさい
KL>=0は知っています。
なので、式(62)の中身に対してKL>=0である事を如何に証明できるかという質問です。
数学では問題そのものを中身とする定理を用いて、"問題証明のプロセス"としないと思います。(ただ、"問題成立の根拠"として同じ内容の定理が引用されるのは論理的に問題ないと思いますが。)
ともり様
ご確認ありがとうございます。
前回の回答と同じことを主張していて恐縮なのですが,もし「式($\ref{eq_KL_gaussian}$)の右辺が非負であることを示せ」という問題が与えられたとすれば,自分であれば式($\ref{eq_KL_gaussian}$)の右辺がKLダイバージェンスで表されることを利用して証明を行うと思います。
つまり,問題を単純化すると,以下のような構造になっています。
問題例:$3^{2}-2\cdot 3\cdot 2+2^{2}\geq 0$であることを示せ
解答例:$3^{2}-2\cdot 3\cdot 2+2^{2}=(3-2)^{2}\geq 0$
いかがでしょうか。
zuka 様
とても分かりやすい解説ありがとうございます。
「Githubで実装を確認する」をクリックしたら出てくるコードを、vs codeで実行して確認したところ、下記のような、デバイスエラーが出力されました。
RuntimeError: Expected all tensors to be on the same device, but found at least two devices, cuda:0 and cpu!
main.pyが「Latest commit 0d3837e on 8 Jan」なので、それよりも古い「Released: Dec 16, 2021」をインストールして再実行しても同様のエラーが出力されました。
実行環境になにか必要な設定などありますか?
一応下記で、teratailの方で一度質問してみたのですが、解決に至らなかったのでご連絡させていただきました。teratail質問記事[ https://teratail.com/questions/8emzaqt1ifsxjd#reply-q1faag0a3kkxw2 ]
tmc5 様
ご質問ありがとうございます!後ほど確認しますね。少々お待ちください。
tmc5 様
お待たせしました。ソースコードを修正しましたので動作確認いただけますでしょうか。よろしくお願い致します。
https://github.com/beginaid/VAE
ご返信いただきありがとうございます!
動作確認できました!ありがとうございます。
zuka様
先ほど返信したtmc5です。
よろしければ、後学のために何が問題だったか簡単に教えていただけると嬉しいです。バージョンの問題だったのでしょうか?
tmc5 様
ご質問ありがとうございます。
原因は,テンソルやモデルを保持するdeviceがCPUとGPU/TPUで混合していたことです。例えば,CPU上のテンソルとGPU上のテンソルを演算しようとすると,「Expected all tensors to be on the same device...」というエラーが出てしまいます。このエラーは,pytorchで実装したDNNベースのモデルをGPU上で動かす際に嫌というほど向き合うことになるエラーですので,ぜひ参考にしてください。
具体的な修正方法は,以下のコミットを参考にしてください。
https://github.com/beginaid/VAE/commit/f0960c13e12aa458018d07969915669bd45e0a00
GPUが利用可能な環境でも,修正前だとZはCPU上に乗ったままでしたので,.to(self.device)を付け加えることで,GPUが利用可能な環境ではGPU上に乗せるように修正しています。
zuka様
ご丁寧にありがとうございます!
納得できました。
zuka 様
お忙しいところ、お返事ありがとうございます❣
> つまり,問題を単純化すると,以下のような構造になっています。
.....
結構啓蒙的なメソッドですね。
厳密的な数学証明にならなくても、問題の本質にある程度突くもっとも簡単な手法かもしれません。
さすがです❣
将来、ここに式(62)に対してKL-D≧0先験的な結論を利用せず、完全な数学証明を下さる方がここに現れたら、尚嬉しいです。
色々良い勉強になりました。
本当にありがとうございました。
ここは宝です。
zuka様
質問失礼します。現在VAEの勉強をしています。理論が難しく、理解できないところが多くあるので的外れな質問になるかもしれませんが回答いただければ幸いです。
VAEではエンコーダによって平均値と分散が得られると思うのですが、学習によって一度潜在空間が構築されればその平均値と分散は1つに決定されるのでしょうか。もしくは学習後、例えばいくつかの訓練データとして用いた画像データをエンコーダによって低次元に落とし込んだ場合、各画像データに対して別々の平均値と分散が決定されるのでしょうか。
なぜこんな疑問が生まれたのかというと、エンコーダによって得られる潜在変数zはz=μ+ε・σ(ただし、εは標準正規分布に従う)で表されると思うのですが、仮に平均値と分散が1つに決定された場合、例えばいくつかの訓練データとして用いた画像データについて考えると各画像データに対する潜在変数zは先ほどの式より平均値μ、分散σ^2の正規分布に従うはずです。ところが自分はkerasを使ってVAEをプログラムしているのですが、学習後にμとσの値をprint()で確認をしようとしても次元数など層としての情報しか確認できません。また、encoder.predict()を使って予測値を出すと、各画像データに対して別々のμとσがどうやら求められているらしく結局μとσが何を表しているのかわからなくなりました。
コードの書き方が違いますし、言ってることもめちゃめちゃかもしれませんがわかる範囲でいいのでどうかよろしくお願いします。
4年生 様
ご質問ありがとうございます!返信遅くなってしまい失礼しました。回答差し上げます。とても良い着眼点だと思いますよ。
>平均値と分散は1つに決定されるのでしょうか
はい。近似事後分布のパラメータは一つに定まります。
>各画像データに対して別々の平均値と分散が決定されるのでしょうか
仮定した確率モデルのパラメータ(母数)と標本値から計算される統計量を混同しているかもしれませんね。各画像データから算出される値は,あくまでも標本値から算出される統計量であり,近似事後分布のパラメータではありません。例えば,正規分布の分散を(不偏分散で)推定する問題を考えます。この際,標本分散と母分散の推定値は異なりますよね。「期待値をとると等価になる」という不偏性を基準に母分散を推定すると,標本分散を$n/(n-1)$倍したものが母分散の推定値になり,この値を不偏分散とよびます。不偏分散以外にも,母分散を標本値から推定する方法は作ろうと思えばいくらでも作れます。このように,母数と標本値を区別することが何よりも大切です。
>仮に平均値と分散が1つに決定された場合、例えばいくつかの訓練データとして用いた画像データについて考えると各画像データに対する潜在変数zは先ほどの式より平均値$\mu$、分散$\sigma^2$の正規分布に従うはずです。
ここは正解に近い言語化をされていると思います。「各画像データに対する潜在変数$z$」というのは,「各画像データに対する潜在変数の実現値$z$」ということですよね。実現値は確率変数ではありませんので,各画像ごとに異なる値が求まるはずです。これが本稿における潜在空間のwalk throughで行っていることです。
>学習後に$\mu$と$\sigma$の値をprint()で確認をしようとしても次元数など層としての情報しか確認できません。
これはKerasの仕様だと思います。pytorchであればサポートできますので,ぜひ私のコードを参考に中身を確認してみてほしいです。
>各画像データに対して別々のμとσがどうやら求められているらしく結局μとσが何を表しているのかわからなくなりました。
本当にそうでしょうか?モデルを推論モードに切り替えていますか??私のコードでは,
-----
self.enc_fc3_mean = nn.Linear(200, z_dim) # 近似事後分布の平均
self.enc_fc3_logvar = nn.Linear(200, z_dim) # 近似事後分布の分散の対数
-----
が近似事後分布の$\mu$と$\sigma$を出力している箇所です。モデルを推論モードにすればnn.Linearのパラメータは固定されますので,必ず毎回同じ値を出力するはずです。今一度確認してみてください!
zuka様
丁寧な回答ありがとうございます!
いただいたアドバイス参考にしてもう一度じっくり考えてみようと思います!
zuka様
本サイト、大変ためになりました。
ところで、私は統計にあまり詳しくないものなので、ちょっとわからないところがあります。
(35)式のところで、$V[\sigma_{\varphi}]$と$V[\mu_{\varphi}]$があります。
それが、(36)式と(37)式でそれぞれが$\sigma^{2}_{\varphi}$と$0$になるようです。
どうしてそうなるのかご教示頂けないでしょうか。
よろしくお願いします。
maty 様
ご質問ありがとうございます。まず,$V[\sigma_{\varphi}]=\sigma^2_{\varphi}$に関しては,期待値と分散の性質期待値と分散の性質をご参照ください。具体的には,
\begin{align}
V[aX] &= a^2V[X]
\end{align}
を利用しています。次に,$V[\mu_{\varphi}]=0$に関しては,期待値と分散の性質と併せて式(23)と式(24)をご参照ください。具体的には,
\begin{align}
V[c] &= 0
\end{align}
と$\mu_{\varphi}=0$を利用しています。以上,ご確認いただけますでしょうか。
非常にわかりやすい説明ありがとうございました。reparameterization trickについて質問です。reparameterization trickは微分可能な定式化のため、エンコーダの近似事後分布で疑似的にガウス分布からサンプリングするとの事ですが、デコーダの尤度関数にも同じ処理をする必要はないでしょうか?また、今回尤度関数にベルヌーイ分布を指定していますが、それはMNISTが白と黒の2値で出力する必要があるからでしょうか?
会社員 様
ご質問ありがとうございます。
>デコーダの尤度関数にも同じ処理をする必要はないでしょうか?
ないと思います。エンコーダ側では潜在変数$z$をサンプリングする必要があるため,Reparameterization trickを利用しました。一方,デコーダ側ではサンプリングの必要がないため,Reparameterization trickを利用しなくてもよいです。
>今回尤度関数にベルヌーイ分布を指定していますが、それはMNISTが白と黒の2値で出力する必要があるからでしょうか?
おっしゃる通りです。VAEでは,学習対象のデータをよく観察して確率分布をフィッティングさせる必要があります(そしてこの変文推論としての拡張性の高さこそがVAEの真髄だと思っています)。
zuka 様
質問に対する丁寧なご回答ありがとうございます。
尤度関数からサンプリングするとなると、確かによくわかりませんね。確率とは違う概念である事を再確認しました。
ベルヌーイ分布の内容はしっかり本ページに書かれていました。重複してご回答させてしまい申し訳ありません。
zuka様
大変勉強になる記事をありがとうございます。
潜在変数に使う平均と分散に関して質問させてください。
self.enc_fc3_mean = nn.Linear(200, z_dim) # 近似事後分布の平均
self.enc_fc3_logvar = nn.Linear(200, z_dim) # 近似事後分布の分散の対数
と実装されていると読み取りました。
meanに関しては、重みと値の総和が期待値?になり、平均として扱えるのかなと思いました。
しかし、分散の対数がnn.Linearで求められるという所が腑に落ちません。また、code中で対数化している箇所も見あたらないように思えます。そもそも同じ入力で、同じnn.Linearの構造に入れ、平均なのか、標準偏差もしくは分散なのか区別できるのでしょうか?
他の実装方法として、softplus関数を組み込む実装もあるかと思いますが、本コードではみつかりません。
self.enc_fc3_logvar = nn.Linear(200, z_dim)の一行で分散の対数を算出できるのでしょうか?もしくはコードの他の部分と組み合わさって算出されているのであればその流れについてご解説お願いします。
また、これらを独立して用意しているのは、学習過程でそれぞれ重み及びバイアスを更新したいからという理解でよいでしょうか。
KU生 さま
ご質問ありがとうございます。一つずつお答えしていきますね。
>分散の対数がnn.Linearで求められるという所が腑に落ちません。
Linearを用いているのは,私が勝手にそのような設計にしているからであり,全結合層である必然性は全くありません。
>code中で対数化している箇所も見あたらない
はい。「VAEのネットワーク構成」の図でも表している通り,Linearの出力を分散の対数として定めています。
>そもそも同じ入力で、同じnn.Linearの構造に入れ、平均なのか、標準偏差もしくは分散なのか区別できるのでしょうか?
少しだけDNNの仕組みを誤解されている可能性があります。「二つのLinearから出てくる値がそれぞれ近似事後分布の平均および分散の対数」となるようにnetworkの学習が進むのです。
>softplus関数を組み込む実装もあるかと思いますが、本コードではみつかりません。
本文に理由は記載しておりますので,ご参照ください。
-----
全結合層のみから構成される非常にシンプルなネットワークです。設計にはいくつかのポイントがあります。まず,エンコーダが分散を出力する部分は分散の対数を出力するようにします。これは,分散に非負制約があるためです。softplusなどを利用すれば,非負制約を満たしたうえで分散そのものを出力するように設計することはできますが,無理に非負制約がある変数を利用する理由もありませんし,pytorchのVAE実装例でも分散の対数を出力するようにしていることを踏まえると,上記設定が自然と思われます。
-----
>self.enc_fc3_logvar = nn.Linear(200, z_dim)の一行で分散の対数を算出できるのでしょうか?
はい。おっしゃる通りです。
>これらを独立して用意しているのは、学習過程でそれぞれ重み及びバイアスを更新したいから
はい。おっしゃる通りです。一つの全結合層でも学習は可能だと思いますが,それぞれ分けてしまった方が学習は容易だと思います。
zuka様
ご返信ありがとうございます。
>少しだけDNNの仕組みを誤解されている可能性があります。「二つのLinearから出てくる値がそれぞれ近似事後分布の平均および分散の対数」となるようにnetworkの学習が進むのです。
この解説でなんとなく理解できたように思います。
私はいわゆる統計学で習う式(平均は平均を求める式を、分散の対数は分散を求める式で算出し、対数化する)を当てはめる必要があると思っていました。
VAEでは必ずしもそのような式ではなく、一つの値を算出する学習可能な式であれば良いということですね。
zuka様 参考になる記事ありがとうございます。
さて、式(13)~式(17)において p_\theta(Z)と表記されていますが、\thetaはXに関するパラメータなのっで、単純にp(Z)でよいのではないでしょうか。 ご回答いただければ幸いです。
また、式(15),(16)の符号が間違っていると思います。
maru様
ご指摘誠にありがとうございます。いずれも仰る通りでしたので,本文を修正致しました。助かりましたmm
zuka 様
記事大変勉強になりました。
デコーダの尤度関数にベルヌーイ分布を指定しているところがどうしても理解できません。
ベルヌーイ分布はXが0or1の離散値だと理解しております。
それにたいしてMNISTのX記事にもあるように 0~1の実数値です。
なぜベルヌーイ分布が仮定できるのかご教示ください。
ベイズ統計初心者 様
ご質問ありがとうございます。
>ベルヌーイ分布はXが0or1の離散値だと理解しております。
おっしゃる通りです。しかしながら,VAEでは「分布のパラメータ」を学習します。分布の出力を学習する訳ではありません。デコーダはベルヌーイ分布のパラメータを学習しますので,sigmoidを利用して$\lambda_{\theta}\in[0,1]$となるように設定しています。
zuka様
返信ありがとうございました。
デコーダの尤度関数にベルヌーイ分布を仮定したことについて再度ご教示ください。
$p_\theta(x|z) = {\lambda_\theta}^x(1-\lambda_\theta)^{(1-x)}$
デコーダのニューラルネットワークがベルヌーイ分布のパラメータ $\lambda$ を出力していることは理解しました。
上式において x は 0 or 1 の離散値であるのに対して NMIST のデータは 0 or 1 ではなく、実数値であるのに
どうして尤度関数としてベルヌーイ分布が仮定できるのかがよく理解できません。
白黒画像なので入力$x$ は、ほぼほぼ2値とみなせるということでしょうか?
再三で申し訳ございません。
ベイズ統計初心者 様
ご質問ありがとうございます。
> $x$は$0$or$1$の離散値であるのに対してNMISTのデータは$0$or$1$ではなく、実数値であるのにどうして尤度関数としてベルヌーイ分布が仮定できるのかがよく理解できません。
実際にデコーダからの出力を得るためには、確率分布からのサンプリングが必要です。本記事では、「デコーダで学習したパラメータで定義されるベルヌーイ分布から各セルの値をサンプリングしたいが、代表点としてベルヌーイ分布の期待値を利用する」という方針を採用しています。ベルヌーイ分布の期待値は、ベルヌーイ分布のパラメータそのものになりますので、今回でいうと$\lambda_{\theta}$がそのままベルヌーイ分布の期待値として各セルの値となります。
ZUKA様
丁寧で分かりやすい説明であり、こちらのサイトはよく参考にさせていただいております。
2点ほど質問させていただきたく。
1 VAEの提案論文(Auto-Encoding Variational Bayes)では同じようなNMISTのデータに対して、(エンコーダ・デコーダそれぞれ)隠れ層が1層となっているようでした。(エンコーダ・デコーダそれぞれ)ZUKA様のモデルでは隠れ層を2つにしたのには何か理由があるのでしょうか?
2 同様に提案論文では活性化関数にtanh関数(双曲線正接関数)を使っているようでした。ZUKA様のモデルでは活性化関数にLeRU関数を利用しているのは何か理由があるのでしょうか?
私の提案論文に対する理解が間違っていたら、申し訳ございません。(ZUKA様のモデルが提案論文を忠実に再現しているだけの場合)
O-Haru様
提案論文に基づいたご指摘ありがとうございます!
1
隠れ層を2層にした大きな理由はありません。経験的に1層では表現力が足りなくなってしまうことが多く,無意識に1層を避けていました。MNIST程度であれば1層でも表現力は十分だと思います。
2
勾配消失問題を避けるためです。おっしゃる通り,厳密に提案論文の再現実装するのであればtanhでも問題ないです。
zuka様
大変勉強になる記事ありがとうございます。
私は損失関数の部分で困っていることがあり、コメントさせていただきました。
再構築誤差(交差エントロピー誤差)+klダイバージェンス
を損失関数として学習するといろいろな画像の入力から入力とはかけ離れたすべて同じ画像が出力されます。
そこで、klダイバージェンスに1/1000の重みづけをしたところ入力画像に対して適切な出力画像が得られました。(ほぼ同じ画像)
しかしこれはVAEと言えるのでしょうか?
私はAEとほぼ同じ状態と認識しています。(klダイバージェンスを無視している状態に近いため)
そこで「posterior collapseを防ぐためには,学習初期はKLダイバージェンスの項を小さく重みづけをして,徐々に大きくしていくという工夫をしてあげる必要があります。」
という部分をzuka様の記事で拝見したのですが、
この学習初期に小さく、徐々に大きくするというのはエポック数ごとにということでしょうか?
それとも小さい係数のklダイバージェンスで学習を1通りし、posterior collapseが起こらなければ、
klダイバージェンスの係数を大きくして学習を繰り返していくということでしょうか?
VAE初学者様
ご質問ありがとうございます。
>しかしこれはVAEと言えるのでしょうか?私はAEとほぼ同じ状態と認識しています。(klダイバージェンスを無視している状態に近いため)
再構成誤差とklダイバージェンスそれぞれのlossの値は確認されましたでしょうか。
実装ミスにより、KLダイバージェンスの項が再構成誤差と比べてオーダーが大きくなっている可能性があります。実際のlossの値を観察しないと「AEとほぼ同じ状態」と断言はできないと思います。また、潜在空間を可視化することにより、KLダイバージェンスによる正則化が効いているかどうかを定性的に確認することも可能です。
>学習初期に小さく、徐々に大きくするというのはエポック数ごとにということでしょうか?それとも小さい係数のklダイバージェンスで学習を1通りし、posterior collapseが起こらなければ、klダイバージェンスの係数を大きくして学習を繰り返していくということでしょうか?
本文としては前者を意図しましたが、後者のように再学習を行う手法もあると思います。いずれにせよ、再構成誤差とKLダイバージェンスそれぞれのlossを観察するところから始めるとよいと思います。