本記事は機械学習の徹底解説シリーズに含まれます。
初学者の分かりやすさを優先するため,多少正確でない表現が混在することがあります。もし致命的な間違いがあればご指摘いただけると助かります。
はじめに
機械学習を勉強したことのある方であれば,EMアルゴリズムの難しさには辟易したことがあるでしょう。私自身,学部生時代に意気揚々と機械学習のバイブルと言われている「パターン認識と機械学習(通称PRML)」を手に取って中身をペラペラめくってみたのですが,あまりの難しさから途方に暮れてしまったのを覚えています。多くの書籍やWeb上の資料では式変形の行間が詰まっていないことがあるため,ほとんどの初学者はEMアルゴリズムで躓くと言っても過言ではありません。
この問題を解決するため,本稿ではEMアルゴリズムをはじめからていねいに説明していきます。具体的には「この解説を読んだだけでEMアルゴリズムの概要と実際の応用方法が理解できる」状態を目指します。多少記事が長くなってしまいますが,ゆっくり自分のペースで読み進めていけば,必ずEMアルゴリズムを理解できるはずです。
EMアルゴリズムがどのような枠組みで何のために用いられるのかを説明します。
最尤推定・MAP推定を実現するための枠組みについて説明します。
混合ガウス分布を例にとってEMアルゴリズムの使い方を確認します。
pythonを使ってEMアルゴリズムを実装します。
EMアルゴリズムの目的
本章では,EMアルゴリズムがどのような目的で用いられるのかを説明します。先に結論からお伝えすると,EMアルゴリズムとは確率モデルの潜在変数・パラメータに関する最尤推定を行うための手法です。そこで,まず最初に確率モデルと最尤推定に関する説明から始めていきます。
確率モデルというのは「現象の裏側に何か適当な分布を仮定する」枠組みのことです。私たちの目的は,ある現象を確率分布を用いて記述することです。そのためには,以下のステップが必要になります。
- ある現象をよく観察して最もよくフィットする既存の確率分布を選択する
- 仮定した確率分布の形状を決定するパラメータを推定する
ある現象に対して既存の分布を仮定するという操作は,観測データの発生方法に対して尤度関数を定めることに相当します。すると,私たちの最終的な目的は分布の形状を決定するパラメータを推定することになります。
尤度関数と同時にパラメータの情報を与える事前分布を設定すると,同時分布を定めることに相当します。ここでは,ある現象に対する既存の分布として尤度関数を定めていますが,ベイズ推定を行う場合には既存の分布として同時分布を定めます。
パラメータの推定方法は,パラメータを1つの値に決め切ってしまう点推定と,パラメータ自体にも既存の分布を仮定するベイズ推定に分けられます。さらに,点推定は尤度関数を最大にする最尤推定と事後確率を最大にする最大事後確率(MAP: maximum a posteriori)推定に分けられます。
- 点推定
- 最尤推定
- MAP推定
- ベイズ推定
以下では,数式を用いて点推定とベイズ推定を説明していきます。
点推定
あるパラメータ$\theta$が与えられたときに,観測データ$X$のふるまいを定義する関数$p(X|\theta)$が尤度関数です。最尤推定では,尤度関数$p(X|\theta)$を最大にする$\theta$の値を求めます。
\hat{\theta}_{\ML} &= \argmaxTheta p(X | \theta)
\end{align}
条件付き確率の定義より,$p(X | \theta)$は「$\theta$が与えられたときの$X$」の確率を表します。言い換えれば「$\theta$が与えられたときに$X$はどれだけ尤もらしいか」を表しています。最尤推定では,条件付けられた$\theta$を変数として読み替えることで,データ$X$に対して最も尤もらしいパラメータ$\theta$を推定します。
$p(X|\theta)$を関数と呼ぶことに違和感がある人は鋭い視点をお持ちです。測度論を用いると,確率は可測空間上の確率測度(つまり関数)として定義されます。測度論を用いない場合の確率$p$の定義はこちらからご確認ください。
一方で,MAP推定では事後確率$p(\theta|X)$を最大にする$\theta$の値を求めます。
\hat{\theta}_{\MAP} &= \argmaxTheta p(\theta | X) \\[0.7em]
&= \argmaxTheta \frac{p(X | \theta)p(\theta)}{p(X)} \\[0.7em]
&= \argmaxTheta p(X | \theta) p(\theta)
\end{align}
ただし,変形にはベイズの定理を利用しました。$\theta$に関する最大化問題であるため,最終行では$p(X)$を無視しました。
計算を簡単にするため,最尤推定やMAP推定では両辺の対数を取った対数尤度関数や対数事後確率を最大化することが多いです。対数関数は単調増加関数であるため,対数を取る前後の最大最小問題は等価になります。
\hat{\theta}_{\ML} &= \argmaxTheta \ln p(X | \theta) \\[0.7em]
\hat{\theta}_{\MAP} &= \argmaxTheta \left\{ \ln p(X | \theta) + \ln p(\theta) \right\}
\end{align}
確率モデルをうまく設定できれば,これらの点推定は解析的に解くことも可能です。例えば,正規分布の形状を決定する母平均の最尤推定量は標本平均に一致し,母分散の最尤推定量は標本分散に一致します。これらはラグランジュの未定乗数法を用いて証明されます。
ベイズ推定
ベイズ推定では,点推定とは異なりパラメータを値ではなく分布として求めることで,データへの過学習を防止したり,表現力を上げたりすることができます。パラメータの分布というのは,ある観測データ$X$が得られたときの事後分布$p(\theta | X)$のことを表しています。
p(\theta | X) &= \frac{p(X | \theta)p(\theta)}{p(X)}
\end{align}
点推定とは異なり,ベイズ推定では$\arg \max$が付いていませんね。$\arg \max$・$\arg \min$は目的関数が最大・最小になるパラメータを値として求めることを意味しています。耳が痛いようですが,ベイズ推定では仮定した確率分布$p$の形状を決めるパラメータ$\theta$の事後分布$p(\theta | X)$を求めます。
点推定の限界として,対象とする現象が多峰性のふるまいを示しているケースが挙げられます。多峰性とは,複数のピークをもつ性質のことを指します。多峰性の現象に対して点推定を行うと,1つのピーク以外の情報を完全に捨て去ってしまいます。
各種推定方法の実現
本章では,各種パラメータの推定方法がどのように実現されるのかについて説明します。先に結論からお伝えすると,点推定を実現する方法はEMアルゴリズム,ベイズ推定を実現する方法は変分ベイズがよく利用されます。
- 点推定
- EMアルゴリズム
- ベイズ推定
- 変分ベイズ(変分推論)
確率モデルの問題を考えるときには,まず最初に確率モデルに潜在変数$Z$(尤度関数に姿を現さない変数)を導入します。そうすることで,複雑な分布をより単純な分布を使って表すことが可能になります。
潜在変数を導入することは,同時分布$p(X,Z)$を設計することに相当します。ここが全ての始まりです。観測データ$X$と潜在変数$Z$にどのような依存関係があるのかを同時分布として設定してしまうわけです。
ベイズ推定では,副次的に尤度関数$p(X|Z)$と事前分布$p(Z)$を仮定することになります。
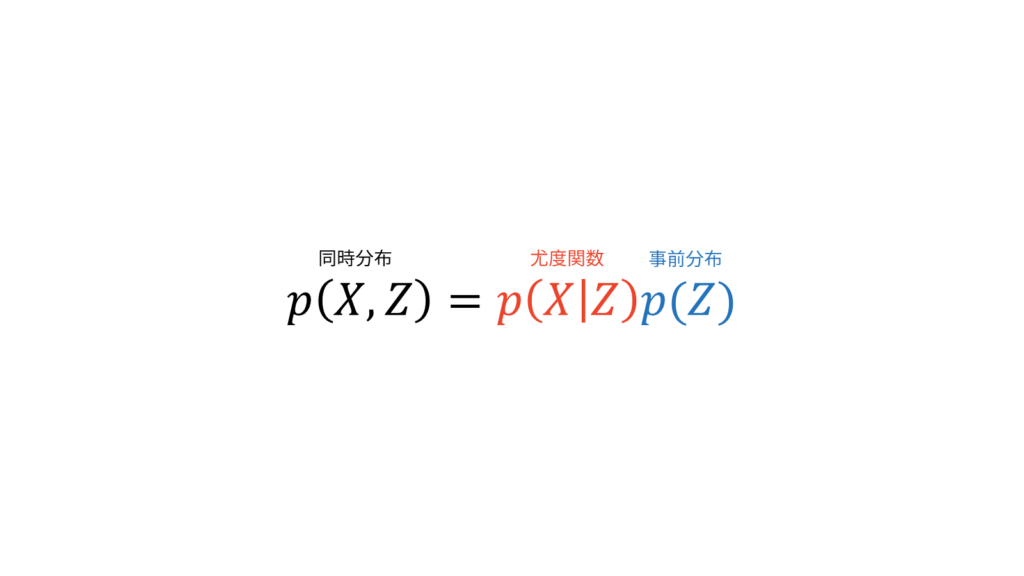
尤度関数と事前分布を定めることは,同時分布を定めることだけでなく,事後分布の形を定めることにも相当します。なぜなら,$X$が観測データであることから$p(X)$は定数だからです。
p(Z|X) &= \frac{p(X, Z)}{p(X)} \\[0.7em]
&\propto p(X, Z) \\[0.7em]
&= p(X|Z)p(Z)
\end{align}
点推定では,事前分布が無情報(定数)だと仮定します。結局,上でお伝えしたように,点推定では同時分布を設計することは尤度関数を設定することに相当します。
p(X, Z) &= p(X|Z)p(Z) \\[0.7em]
&= p(X|Z)\cdot \const \\[0.7em]
&\propto p(X|Z)
\end{align}
本題に入っていきます。結論からお伝えすると,EMアルゴリズムは以下の流れで計算されます。
潜在変数を含む点推定では,交互操作で下限を最大化するEMアルゴリズムが用いられる。まず$\theta^{\old}$を初期化した後に,以下のステップを収束条件を満たすまで繰り返す。
Eステップ
事後確率と$\calQ$関数を計算する。
q^{\ast}(Z) &= p(Z | X, \theta^{\old}) \\[0.7em]
\calQ_{\ML}(\theta, \theta^{\old}) &= E_{Z|X, \theta^{\old}} \left[ \ln p(X, Z | \theta) \right]
\end{align}
Mステップ
最尤推定の場合
\theta^{\new} &= \argmaxTheta \calQ_{\ML}(\theta, \theta^{\old})
\end{align}
MAP推定の場合
\theta^{\new} &= \argmaxTheta \left\{ \calQ_{\ML}(\theta, \theta^{\old}) + \ln p(\theta) \right\}
\end{align}
ここからは,EMアルゴリズムが上の流れで実現されることを説明していきます。
最尤推定
まずは,点推定の中でも最尤推定について注目していきます。最尤推定では,対数尤度関数$\ln p(X | \theta)$を最大にすることが目的でした。潜在変数を導入するため,対数尤度関数を潜在変数で周辺化したものとみなしましょう。ここでは,潜在変数は離散型変数とします。連続型変数にしても,シグマをインテグラルに対応させるだけで同様の議論が可能です。
\hat{\theta}_{\ML} &= \argmaxTheta \ln p(X | \theta) \\[0.7em]
&= \argmaxTheta \ln \sum_{Z} p(X, Z | \theta) \quad && (\because~\text{周辺化}) \label{eq_ML_marginalize}
\end{alignat}
しかし,ここで困ったことがあります。右辺に$\ln \sum$という項が出てきてしまいました。一般に,$\ln \sum$の計算は困難とされています。この問題を解決するため,EMアルゴリズムでは対数尤度を下から評価した下限を最大化していくことで,間接的に対数尤度を最大化していきます。
私は「下限(lower limit)」という用語の濫用に問題意識を感じています。多くの日本語の資料では,目的関数を下から評価した関数を下限と表現しています。下限は下界の最大値ですので,何も考えずに下限としてしまうのは危険です。イェンセンの不等式のように,下から評価した関数が目的関数と同じ値を取りうる場合はたしかに下限になるのですが,一般的には「下界(lower bound)」になります。例えば,後に出てくるvariational lower boundは日本語では変分下限と訳されています。しかし,正確に訳すと変分下界になるはずです。このように,英語と日本語で下限と下界の表記揺れがあるため注意が必要です。本稿では,読者の混乱を防ぐために,目的関数を下から評価した関数は一律で下限と表現します。
数理最適化の分野では,ある関数を下から評価するためにイェンセン(Jensen)の不等式が利用されます。イェンセンの不等式は,上に凸な関数に対して定義される不等式です。「2点を結ぶ内分点」よりも「2点を結んだ内分点の関数を通した値」の方が大きくなるという主張を一般化したものといえます。
$f(x)$が上に凸な関数のとき,任意の$x_1, \ldots, x_n$と$\lambda_i{\geq}0$かつ$\sum_{i=1}^{n}\lambda_{i}{=}1$を満たす任意の$\lambda_1, \ldots, \lambda_n$に対して次が成り立つ。
f\left( \sum_{i=1}^{n} \lambda_i x_i \right) \geq \sum_{i=1}^{n} \lambda_i f(x_i)
\end{align}
式($\ref{eq_ML_marginalize}$)にイェンセンの不等式を適用することを考えます。まず,上に凸な関数$f$として$\ln (\cdot)$を考えます。式($\ref{eq_ML_marginalize}$)とイェンセンの不等式の形を見比べると,足して$1$になる係数$\lambda_i$が不足していることが分かります。
そこで,式($\ref{eq_ML_marginalize}$)に対して足して$1$になる係数を準備します。変分ベイズへの拡張性を踏まえて,ここでは$q(Z)$という確率分布を持ち出します。確率分布は確率変数に対する総和・積分が$1$になりますので,足して$1$になる係数として丁度良いのです。
\ln \sum_{Z} p(X, Z | \theta) &= \ln \sum_{Z} q(Z) \frac{p(X, Z | \theta)}{q(Z)} \label{eq_before_jensen}
\end{align}
すると,式($\ref{eq_before_jensen}$)はイェンセンの不等式における左辺の形になっていることが分かります。イェンセンの不等式を適用しましょう。
\ln \sum_{Z} q(Z) \frac{p(X, Z | \theta)}{q(Z)}
&\geq \sum_{Z} q(Z) \ln \frac{p(X, Z | \theta)}{q(Z)} \quad && (\because~\text{イェンせンの不等式}) \\[0.7em]
&\equiv \calL_{\ML} \left[ q(Z), \theta \right] \label{def_l_ml}
\end{alignat}
ただし,得られた下限を$\calL_{\ML}[ q(Z), \theta]$とおきました。この$q(Z)$の持ち出し方がポイントです。多くの説明では天下り的に$q(Z)$が降ってくると思うのですが,EMアルゴリズムの文脈における$q(Z)$はあくまでも「足して$1$になる何か」という意味合いで持ち出されることに注意してください。
対数尤度関数を最大にするためには,下限を最大化すればよいのですが,ここでは対数尤度と下限の関係性についてもう少し解像度を上げてみたいと思います。下限がどれだけ大きくなっているかを評価するためには,対数尤度関数と下限の差を評価する必要があります。
&\ln p(X | \theta)-\calL_{\ML} \left[ q(Z), \theta \right] \notag \\[0.7em]
&= \ln p(X | \theta)-\sum_{Z} q(Z) \ln \frac{p(X, Z | \theta)}{q(Z)} \\[0.7em]
&= \ln p(X | \theta) \sum_{Z}q(Z)-\sum_{Z} q(Z) \ln \frac{p(X, Z | \theta)}{q(Z)} \\[0.7em]
&= \sum_{Z}q(Z)\ln p(X | \theta)-\sum_{Z} q(Z) \ln \frac{p( Z | X, \theta)p(X | \theta)}{q(Z)} \\[0.7em]
&= \sum_{Z}q(Z)\ln p(X | \theta)-\sum_{Z} q(Z) \left\{ \ln p(Z | X, \theta) + \ln p(X | \theta)-\ln q(Z) \right\} \\[0.7em]
&= -\sum_{Z} q(Z) \left\{-\ln p(X | \theta) + \ln p(Z | X, \theta) + \ln p(X | \theta)-\ln q(Z) \right\} \\[0.7em]
&=-\sum_{Z} q(Z) \ln \frac{p(Z | X, \theta)}{q(Z)} \\[0.7em]
&= \KL \left. \left[ q(Z) \right\| p(Z|X, \theta) \right]
\end{align}
ただし,以下のKLダイバージェンスの定義を利用しました。
離散型確率分布$p(X)$,$q(X)$に対して,KLダイバージェンスは以下のように定義される。
\KL \left. \left[ q(X) \right\| p(X) \right] &= \sum_{X} q(X) \log \frac{q(X)}{p(X)}
\end{align}
なんと,対数尤度関数と下限の差は,近似事後分布と真の事後分布のKLダイバージェンスと一致しました。非常に美しい結果です。一般に,KLダイバージェンスは負の値を取りませんから,下限はどれだけ頑張っても対数尤度関数より大きくなることはありません。これはイェンセンの不等式と矛盾しませんね。
KLダイバージェンスについて少し補足しておきます。2つの分布間の離れ具合を測るKLダイバージェンスは,2つの分布を入れ替えると異なる値になることがあり,距離の公理を満たさないことから数学的な距離とはいえません。しかし,情報理論の世界において自然に導入される概念であることなどから,KLダイバージェンスが「距離のような尺度」として用いられることは珍しくありません。
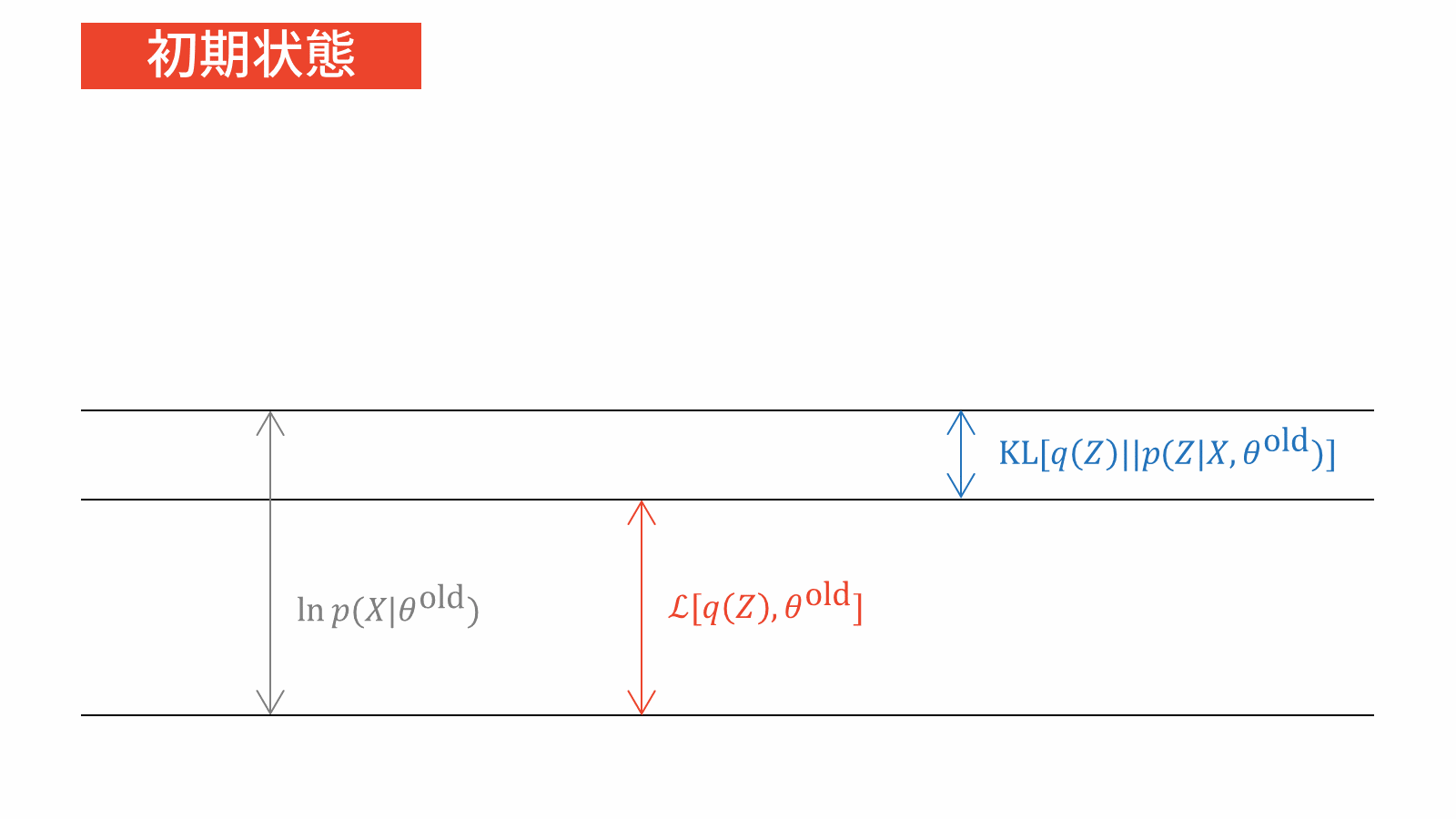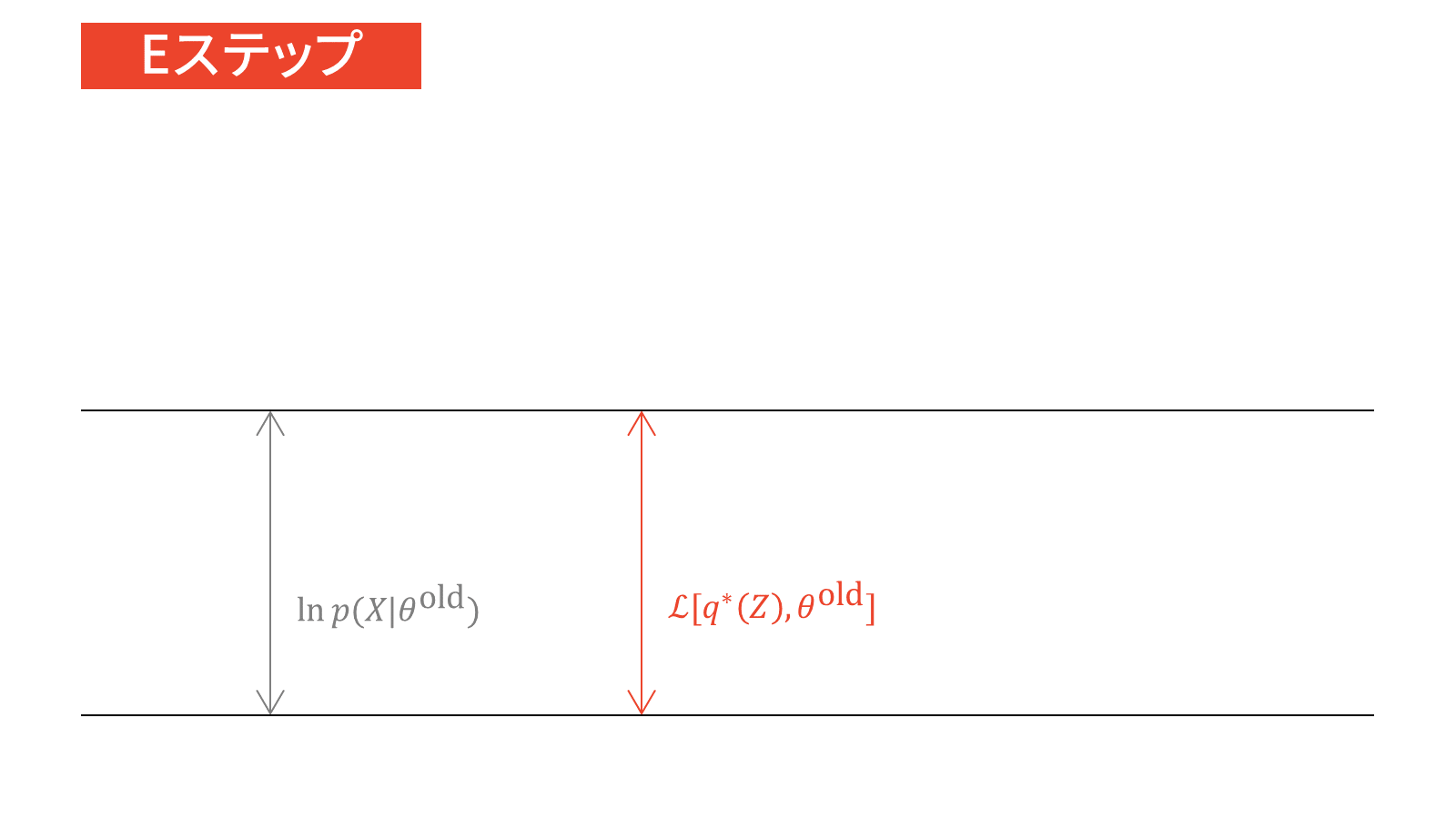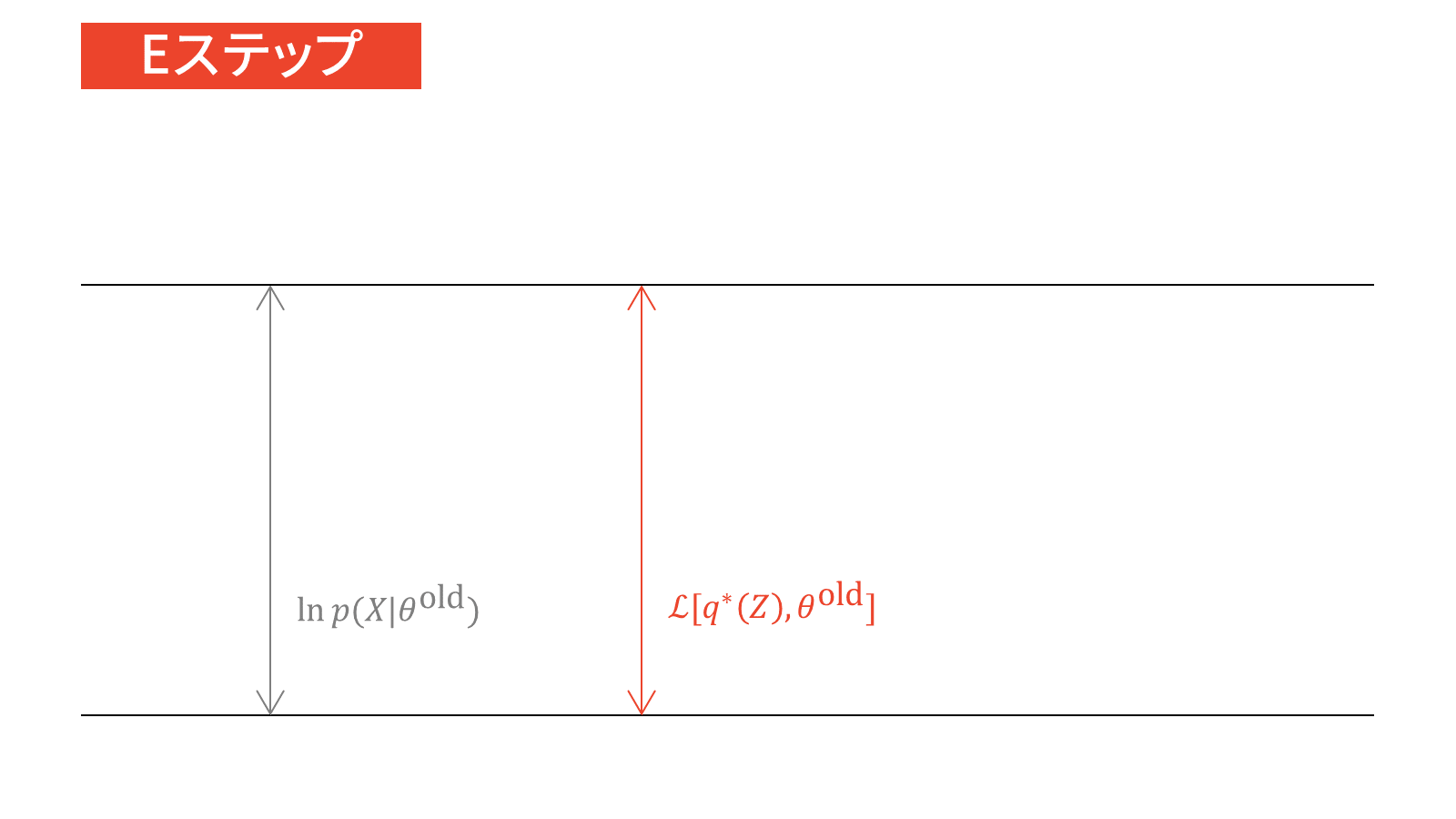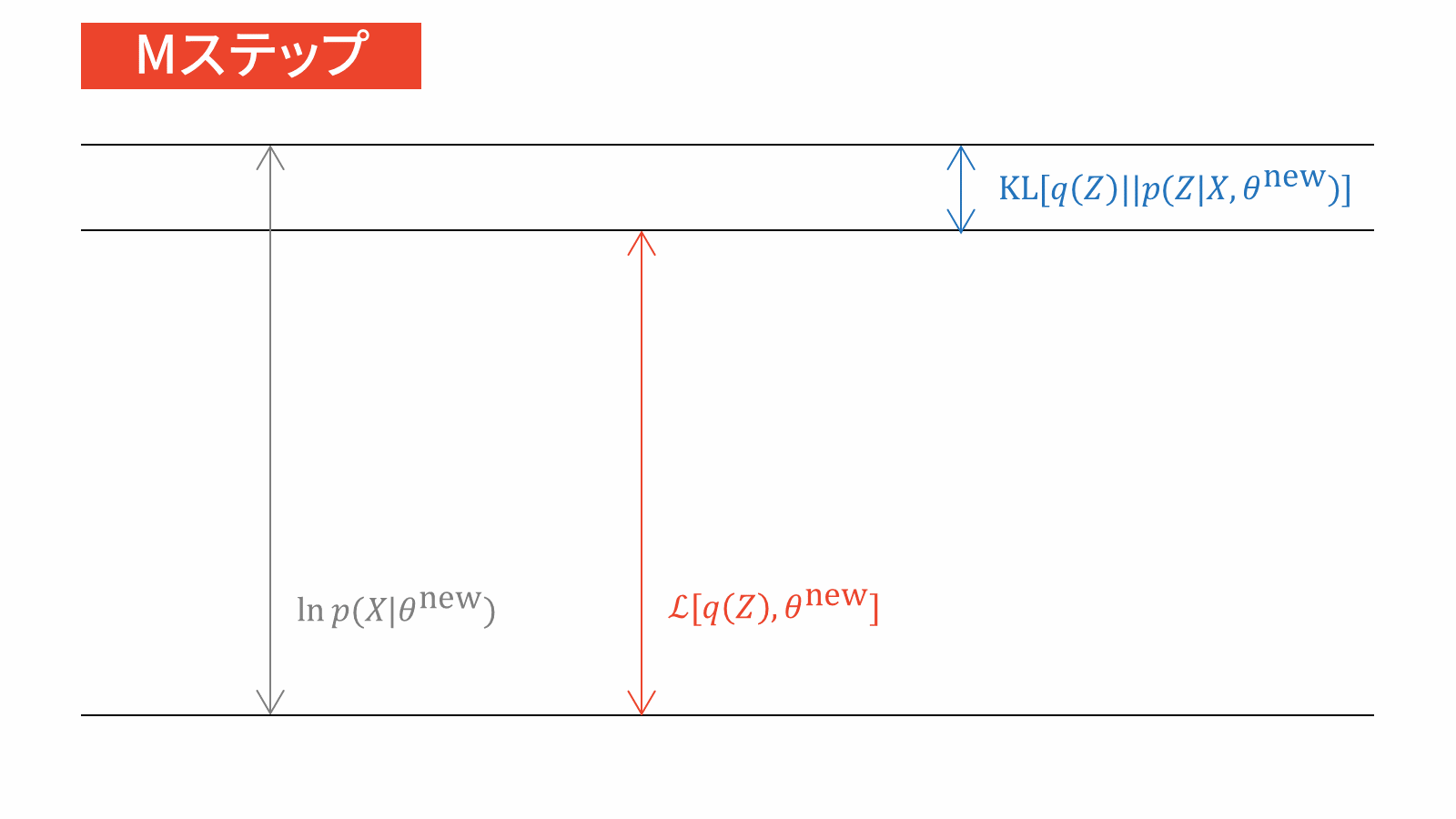
話を元に戻します。対数尤度関数・下限・KLダイバージェンスを可視化すると以下のような関係になっています。

上図を参考にすると,対数尤度関数を最大化するためには下限を最大化する必要がありますが,下限には$q(Z)$と$\theta$という2つの変数が存在します。そこで,2変数関数である下限を効率よく最大化するために,最初にいずれかの変数に注目して最適化を行います。対数尤度関数と下限の差であるKLダイバージェンスは$q(Z)$だけの変数ですので,$\theta$の最適化を行う前にKLダイバージェンスを最小化する(つまり$0$にする)$q(Z)$を選んであげます。
「KLダイバージェンスは$q(Z)$だけの変数」という部分に引っかかるかもしれません。$p(Z|X, \theta)$も変数に入っていると思われるかもしれませんが,$p(Z|X, \theta)$は真の事後分布ですので変数ではなく定数です。
その$q(Z)$を固定したうえで,下限を最大にする$\theta$を求めてあげます。すると,$q(Z)$を固定していたためにKLダイバージェンスが$0$でなくなってしまいますから,再びKLダイバージェンスを最小化してあげます。以下,これらの繰り返しにより対数尤度関数が最大化されていきます。なお,以下のアニメーションではまだ説明していない「Eステップ」と「Mステップ」という用語が使われていますが,後ほど説明しますのでご安心下さい。

これら2つのフェーズについて詳しく見ていきましょう。まずは,KLダイバージェンスを最小化する(つまり$0$にする)フェーズについてです。KLダイバージェンスが$0$となるのは,2つの分布が等しいときですから,最適な$q^{\ast} (Z)$は以下を選べばよいことになります。
q^{\ast} (Z) &= p(Z | X, \theta) \label{eq_em_e_step}
\end{align}
これは,$q$を潜在変数$Z$の事後確率で置き換えることを意味しています。より正確には,$\theta$には初期値もしくは前のフェーズで推定された$\theta^{\old}$が入っていると考えられるため,$q^{\ast} (Z)$は以下のように表されます。
q^{\ast} (Z) &= p(Z | X, \theta^{\old})
\end{align}
ここで重要な考察が得られます。EMアルゴリズムでは,真の事後分布を計算できるという前提が必要になるということです。このような前提のもと,KL最小化フェーズでは潜在変数に関する近似事後分布を計算しています。ちなみに,変分ベイズでは真の事後分布が計算できないという立場を取ります。
次に,下限を最大化するフェーズです。KL最小化フェーズにおいて,最適な$q(Z)$である$q^{\ast}(Z)$は選ばれていますので,最大化する対象は下限に$q^{\ast}(Z)$を代入したものになります。
\calL_{\ML} \left[q ^{\ast}(Z), \theta \right] &= \sum_{Z} q^{\ast} (Z) \ln \frac{p(X, Z | \theta)}{q^{\ast}(Z)} \\[0.7em]
&= \sum_{Z} p(Z|X, \theta^{\old})\ln \frac{p(X, Z | \theta)}{p(Z|X, \theta^{\old})} \\[0.7em]
&= \sum_{Z} p(Z|X, \theta^{\old})\ln p(X, Z | \theta) + \const \\[0.7em]
&= \calQ_{\ML}(\theta, \theta^{\old}) + \const
\end{align}
ただし,定数部以外の$\theta$に関する関数を$\calQ_{\ML}$とおきました。ここで定義された下限の最大化に対応する関数のことを$\calQ$関数と呼びます。$\calQ$関数は最尤推定とMAP推定で別の結果となります。最尤推定における$\calQ$関数は,潜在変数の事後分布に関する対数尤度関数の期待値のことを指しています。
ここまでの流れを整理しましょう。EMアルゴリズムは3つのフェーズから構成されています。
- フェーズ1:
- 事後確率$p(Z | X, \theta^{\old})$の計算
- フェーズ2:
- 対数尤度関数の潜在変数に関する期待値$\calQ_{\ML}(\theta, \theta^{\old})$の計算
- フェーズ3:
- $\calQ_{\ML}(\theta, \theta^{\old})$を最大にする$\theta$の計算
なお,「フェーズ」は一般的な用語ではなく,管理人独自で使用している用語ですのでご注意ください。
フェーズ1の目的はKLダイバージェンスを最小化するため,フェーズ2・フェーズ3の目的は下限を最大化するためです。一方で,フェーズ1・フェーズ2は最終的に対数尤度関数の潜在変数に関する期待値(Expectation)を計算することが目的であることから「Eステップ」と呼ばれています。加えて,フェーズ3はEステップで計算した期待値を最大化(Maximization)することが目的であることから「Mステップ」と呼ばれています。

一般的には,フェーズ2までをEステップとすることが多いです。このことから「KL最小化・下限最大化」と「Eステップ・Mステップ」の切り分け方が一対一対応している訳ではないので注意が必要です。
実際のアルゴリズムではEステップとMステップのどちらから始めても良いのですが,KLダイバージェンスを最小化するパラメータ$\theta^{\old}$の初期値を適当に与えて,Eステップから始めることが多いです。そして,EステップとMステップの交互更新は,対数尤度関数の増加幅に関する収束条件により停止されます。このようなアルゴリズムをEMアルゴリズムと呼びます。
MAP推定
ここまでは点推定の中でも最尤推定に関する内容でしたが,MAP推定も同様にEMアルゴリズムで実現することが可能です。具体的には,対数尤度関数の代わりに対数事後確率を目的関数に設定すれば良いのです。
\ln p(\theta | X) &= \ln \frac{p(X | \theta)p(\theta)}{p(X)} && (\because~\text{ベイズの定理})\\[0.7em]
&= \ln p(X | \theta) + \ln p(\theta)-\ln p(X) \\[0.7em]
&\geq \calL_{\ML} \left[ q(Z), \theta \right] + \ln p(\theta)-\ln p(X) \quad &&(\because~\text{最尤推定の結果}) \\[0.7em]
&\equiv \calL_{\MAP} \left[ q(Z), \theta\right]
\end{alignat}
ただし,対数事後確率の下限を$\calL_{\MAP} [q(Z), \theta]$とおきました。最尤推定のときと同様に,対数事後確率と下限の差を計算します。
\ln p(\theta | X)-\calL_{\MAP} \left[q(Z), \theta \right] &= \left\{ \ln p(X | \theta) + \ln p(\theta)-\ln p(X) \right\} \notag \\[0.7em]
&\quad\quad-\left\{ \calL_{\ML} \left[q(Z), \theta \right] + \ln p(\theta)-\ln p(X) \right\} \\[0.7em]
&= \ln p(X | \theta)-\calL_{\ML} \left[q(Z), \theta \right] \\[0.7em]
&= \KL \left. \left[ q(Z) \right\| p(Z|X,\theta) \right] \quad (\because~\text{最尤推定の結果})
\end{align}
したがって,MAP推定の場合も最尤推定と同じく,目的関数と下限の差はKLダイバージェンスになることが分かりました。一方で,下限を最大化するステップは少し異なる結果となります。
\calL_{\MAP} \left[ q(Z), \theta \right] &= \calL_{\ML} \left[q(Z), \theta \right] + \ln p(\theta)-\ln p(X) \\[0.7em]
&= \calQ_{\ML}(\theta, \theta^{\old}) + \ln p(\theta)-\ln p(X) + \const \quad && (\because~\text{最尤推定の結果}) \\[0.7em]
&= \calQ_{\ML}(\theta, \theta^{\old}) + \ln p(\theta) + \const \quad && (\because~p(X)\text{は定数}) \\[0.7em]
&\equiv \calQ_{\MAP}(\theta, \theta^{\old})
\end{align}
結局,MAP推定における$\calQ$関数は以下のように表されます。
\calQ_{\MAP} &= \calQ_{\ML}(\theta, \theta^{\old}) + \ln p(\theta)
\end{align}
このように,MAP推定の$\calQ$関数は最尤推定の$\calQ$関数に対して事前分布に関する正則化$\ln p(\theta)$を施した手法だといえます。MAP推定ではパラメータのとりうる値の傾向を考慮することができるようになるため,最尤推定よりも汎化性能の高い点推定を実現することが可能です。
以上をまとめると,点推定におけるEMアルゴリズムは以下のようにまとめられます。
潜在変数を含む点推定では,交互操作で下限を最大化するEMアルゴリズムが用いられる。まず$\theta^{\old}$を初期化した後に,以下のステップを収束条件を満たすまで繰り返す。
Eステップ
事後確率と$\calQ$関数を計算する。
q^{\ast}(Z) &= p(Z | X, \theta^{\old}) \\[0.7em]
\calQ_{\ML}(\theta, \theta^{\old}) &= E_{Z|X, \theta^{\old}} \left[ \ln p(X, Z | \theta) \right]
\end{align}
Mステップ
最尤推定の場合
\theta^{\new} &= \argmaxTheta \calQ_{\ML}(\theta, \theta^{\old})
\end{align}
MAP推定の場合
\theta^{\new} &= \argmaxTheta \left\{ \calQ_{\ML}(\theta, \theta^{\old}) + \ln p(\theta) \right\}
\end{align}
混合ガウス分布への適用
本章では,混合ガウス分布(GMM:Gaussian Mixture Model)を題材に,EMアルゴリズムを応用する方法(GMM-EM)をお伝えしていきます。最初に,問題設定と仮定を確認しておきましょう。
$N$個の$D$次元データ$X=\{\vx_1, \ldots, \vx_N\}$が与えられ,$K$個のクラスタに分類します。このときに,与えられたデータは「いくつかのガウス分布からそれぞれ$\pi_k$の確率で生成されたものだ」と仮定するのが混合ガウス分布を利用したクラスタリングです。具体的には,尤度関数として以下の混合ガウス分布を仮定します。
p(X|\vpi, \vmu, \mSigma) &= \prod_{n=1}^{N}\left\{\sum_{k=1}^K \pi_k \N (\vx_n | \vmu_k, \mSigma_k)\right\}
\end{align}
ただし,$\sum_{k=1}^{K}\pi_k = 1$です。ここで,表現力を高めるため,潜在変数として「データ$\vx_n$がクラスタ$k$に属しているか属していないか」を表す$\vz_n$を利用します。$\vz_n$は,one-hot-vector(ある要素だけ$1$で他は$0$となるベクトル)です。$z_{nk}=1$のときは,データ$\vx_n$がクラスタ$k$に属していることを表しています。
$\vz_n$の定義より,潜在変数$z_{nk}$が$1$となる確率が$\pi_k$になります。すなわち,$p(z_{nk}{=}1){=}\pi_k$です。
$\vz_{n}$がone-hot-vectorであることを利用すると,$p(Z|\vtheta)$は以下のように表すこともできます。
p(Z|\vtheta) &= \prod_{n=1}^{N}\prod_{k=1}^{K}\pi_k^{z_{nk}}
\end{align}
ただし,$\vpi$・$\vmu$・$\mSigma$はまとめて$\vtheta$と表すことにしました。次に,$Z$が与えられているとき,すなわち「データ$\vx_n$がどのクラスタ$k$に属しているか」を与えられているときは,$p(X|Z,\vtheta)$は以下のように表されます。
p(X|Z,\vtheta) &= \prod_{n=1}^N\prod_{k=1}^K\N (\vx_{n}| \vmu_k, \mSigma_k)^{z_{nk}}
\end{align}
これらを用いると,$(X,Z)$の尤度関数$p(X,Z|\vtheta)$は以下のように表されます。
p(X,Z|\vtheta) &= P(Z|\vtheta)P(X|Z,\vtheta) = \prod_{n=1}^{N}\prod_{k=1}^{K}\left\{\pi_k\N (\vx_{n}| \vmu_k, \mSigma_k)\right\}^{z_{nk}}
\end{align}
改めて目的を整理します。EMアルゴリズムの目的は,混合ガウス分布のパラメータ(混合係数$\pi_k$・平均$\vmu_k$・共分散行列$\mSigma_k$)を点推定することです。与えられたデータの生成をよく裏付けられるような$K$個のガウス分布の形状を求めることが,今回のミッションです。
Eステップ
早速,Eステップから計算していきましょう。EMアルゴリズムのEステップでは,潜在変数の事後確率を求めてから$\calQ$関数を計算するのでした。$Z$以外を定数とみることで,
p(Z|X, \vtheta) &= \frac{P(X,Z|\vtheta)}{P(X|\vtheta)} \\[0.7em]
&\propto P(X,Z|\vtheta)\\[0.7em]
&= \prod_{n=1}^{N}\prod_{k=1}^{K}\left\{\pi_k\N (\vx_{n}| \vmu_k, \mSigma_k)\right\}^{z_{nk}}
\end{align}
と求められます。次に$\calQ$関数を求めます。$\calQ$関数は対数尤度関数の潜在変数の事後分布に関する期待値でした。
&\calQ(\theta,\theta^{\old})\notag\\[0.7em]
&= E_{Z|X, \theta^{\old}} \left[ \ln p(X, Z | \theta) \right] \\[0.7em]
&= E_{Z|X, \theta^{\old}} \left[ \sum_{n=1}^{N} \sum_{k=1}^{K} z_{nk} \left\{ \ln \pi_{k}+\ln \N(\vx_n | \vmu_{k}, \mSigma_{k}) \right\} \right] \\[0.7em]
&= \sum_{n=1}^{N} \sum_{k=1}^{K} E_{Z|X, \theta^{\old}} [z_{nk}] \left[ \ln\pi_{k}-\frac{1}{2}\left\{D\ln 2\pi+\ln |\mSigma_{k}|+(\vx_n-\vmu_{k})^{T}\mSigma_{k}^{-1}(\vx_{n}-\vmu_{k}) \right\} \right]
\end{align}
$\calQ$関数に出現した$E_{Z|X, \theta^{\old}} [z_{nk}]$も計算しておきましょう。
E_{Z|X, \theta^{\old}} [z_{nk}]
&= \sum_{\vz_{n}} z_{nk} \cdot p(z_{nk}|\vx_n, \vtheta^{\old}) \\[0.7em]
&= \sum_{\vz_{n}} z_{nk} \cdot \frac{p(\vx_n, z_{nk}|\vtheta^{\old})}{p(\vx_{n}|\vtheta^{\old})}\\[0.7em]
&= \sum_{\vz_{n}} z_{nk} \cdot \frac{p(\vx_n, z_{nk}|\vtheta^{\old})}{\sum_{j=1}^{K}p(\vx_{n}, z_{nj}|\vtheta^{\old})}\\[0.7em]
&= \sum_{\vz_{n}}z_{nk}\cdot\frac{\prod_{k^{\prime}=1}^{K}\left\{ \pi_{k^{\prime}}^{\old} \N(\vx_{n} | \vmu_{k^{\prime}}^{\old}, \mSigma_{k^{\prime}}^{\old}) \right\}^{z_{nk^{\prime}}} }{\sum_{j=1}^{K} \pi_{j}^{\old} \N (\vx_n | \vmu_{j}^{\old}, \mSigma_{j}^{\old})} \label{one-hot適用前}\\[0.7em]
&= \frac{\pi_{k}^{\old} \N (\vx_n | \vmu_{k}^{\old}, \mSigma_{k}^{\old})} {\sum_{j=1}^{K} \pi_{j}^{\old} \N (\vx_{n} | \vmu_{j}^{\old}, \mSigma_{j}^{\old})}\label{one-hot適用後}
\end{align}
ただし,式($\ref{one-hot適用前}$)から式($\ref{one-hot適用後}$)への変形には,$\vz_n$がone-hot-vectorであることを利用しました。一般に,$E_{Z|X, \theta^{\old}} [z_{nk}]$は負担率と呼ばれ,$r_{nk}$と書かれます。
r_{nk} &= \frac{\pi_{k}^{\old} \N (\vx_n | \vmu_{k}^{\old}, \mSigma_{k}^{\old})} {\sum_{j=1}^{K} \pi_{j}^{\old} \N (\vx_n | \vmu_{j}^{\old}, \mSigma_{j}^{\old})}
\end{align}
結局,負担率$r_{nk}$を利用すれば$\calQ$関数は以下のように表されます。
\calQ(\theta,\theta^{\old}) &= \sum_{n=1}^{N} \sum_{k=1}^{K} r_{nk} \left[\ln\pi_{k}-\frac{1}{2}\left\{D\ln 2\pi+\ln |\mSigma_{k}|+(\vx_n-\vmu_{k})^{T}\mSigma_{k}^{-1}(\vx_{n}-\vmu_{k}) \right\} \right]
\end{align}
Eステップの最後に,負担率の解釈を考えてみましょう。分母は混合ガウス分布の各クラスタに関する和です。分子は混合ガウス分布のある特定のクラスタの値です。つまり,負担率とは,あるクラスタがデータをどれだけよく説明しているかを全体に占める割合で表した概念です。この負担率を使えば「どのデータ」が「どのクラスタ」に「どの程度」属しているのかを知ることができます。ちなみに,負担率は「$z_{nk}=1$となる事後確率」とも等価です。
r_{nk} &= E_{Z|X, \theta^{\old}}[z_{nk}] \\[0.7em]
&= 1 \cdot p(z_{nk}=1|\vx_n, \vtheta^{\old}) + 0 \cdot p(z_{nk}=0|\vx_n, \vtheta^{\old}) \\[0.7em]
&= p(z_{nk}=1|\vx_n, \vtheta^{\old})
\end{align}
以上で,Eステップを終了します。
Mステップ
Mステップでは,$\calQ$関数を最大化するパラメータ$\theta$を偏微分を利用して求めていきます。このときに注意が必要なのは,パラメータのうち$\pi_k$だけは$\sum_{k=1}^{K} \pi_k = 1$という制限があるという点です。今回は,条件付き最大最小問題を解くうえでオーソドックスな手法の一つであるラグランジュの未定乗数法を利用します。$\calQ$関数に$\sum_{k=1}^{K} \pi_k = 1$の制限をつけたラグランジュ関数を$F$とおくことにします。
F &= \calQ(\vtheta,\vtheta^{\old}) + \lambda \left( \sum_{k=1}^{K} \pi_k-1 \right) \\[0.7em]
&= \sum_{n=1}^{N} \sum_{k=1}^{K} r_{nk} \left[\ln\pi_{k}-\frac{1}{2}\left\{D\ln 2\pi+\ln |\mSigma_{k}|\right.\right.\notag\\[0.7em]
&\quad\quad\quad\quad\left.+(\vx_n-\vmu_{k})^{T}\mSigma_{k}^{-1}(\vx_{n}-\vmu_{k}) \right\} \biggr]+\lambda \left( \sum_{k=1}^{K} \pi_k-1 \right)
\end{align}
実際に計算していきましょう。まずは,$F$を$\vmu_k$について偏微分して$0$とおきます。
\frac{\partial F}{\partial \vmu_k} &= \sum_{n=1}^{N} r_{nk} \cdot \left\{-\frac{1}{2} \cdot 2\mSigma_k^{-1} (\vx_n-\vmu_k) \right\} \\[0.7em]
&= 0
\end{align}
ただし,以下の二次形式に関する微分公式を利用しました。
$A$が対称行列のとき,つぎが成り立つ。
\frac{d}{d \vx} \vx^T A \vx &= 2A\vx
\end{align}
したがって,$\vmu_k$の最適解は以下です。
\vmu_k &= \frac{\sum_{n=1}^{N} r_{nk} \vx_n}{\sum_{n=1}^{N} r_{nk}} \\[0.7em]
&= \frac{\sum_{n=1}^{N} r_{nk} \vx_n}{N_k}
\end{align}
次に,$F$を$\mSigma_k$について偏微分して$0$とおきます。
\frac{\partial F}{\partial \mSigma_k} &= \sum_{n=1}^{N} r_{nk} \cdot \left\{-\frac{1}{2}(\mSigma_{k}^{-1})^{T}+\frac{1}{2}\frac{\partial}{\partial \mSigma_k}(\vx_n-\vmu_k)^T \mSigma_k^{-1}(\vx_n-\vmu_k) \right\} \\[0.7em]
&= \sum_{n=1}^{N} r_{nk} \cdot \left\{-\frac{1}{2}\mSigma_{k}^{-1}+\frac{1}{2} \mSigma_k^{-1} (\vx_n-\vmu_k)(\vx_n-\vmu_k)^T\mSigma_k^{-1} \right\} \\[0.7em]
&= 0
\end{align}
ただし,対称行列の逆行列は対称行列となることと,以下の微分公式を利用しました。
\frac{d}{dA} \ln|A| &= (A^{-1})^{T}\\[0.7em]
\frac{d}{d A} \vx^T A^{-1} \vy &= -A^{-T} \vx \vy^T A^{-T}
\end{align}
したがって,$\mSigma_k$の最適解は以下です。
\mSigma_k &= \frac{\sum_{n=1}^{N} r_{nk} (\vx_n-\vmu_k)(\vx_n-\vmu_k)^T}{\sum_{n=1}^{N} r_{nk}} \\[0.7em]
&= \frac{\sum_{n=1}^{N} r_{nk} (\vx_n-\vmu_k)(\vx_n-\vmu_k)^T}{N_k}
\end{align}
ただし,$N_{k}=\sum_{n=1}^{N} r_{nk}$とおきました。最後に,$F$を$\pi_k$について偏微分して$0$とおきます。
\frac{\partial F}{\partial \pi_k} &= \sum_{n=1}^{N} r_{nk} \frac{1}{\pi_k}+\lambda = 0
\end{align}
両辺に$\pi_{k}$を掛けて整理しておきます。
\sum_{n=1}^{N} r_{nk} +\lambda \pi_k
&= 0 \label{eq_F_pi}
\end{align}
ここで,「足して$1$となる制約があるラグランジュ未定乗数法」でよく利用される式変形なのですが,式(\ref{eq_F_pi})の両辺で$k$に関して総和をとります。
\sum_{k=1}^{K} \left\{ \sum_{n=1}^{N} r_{nk} +\lambda \pi_k \right\}
&= \sum_{n=1}^{N} \sum_{k=1}^{K} r_{nk} + \lambda = 0
\end{align}
したがって,$\lambda$は以下のように表されます。
\lambda &= -\sum_{n=1}^{N} \sum_{k=1}^{K} r_{nk} \label{def_lambda}
\end{align}
式($\ref{def_lambda}$)を式(\ref{eq_F_pi})に代入すると,$\pi_k$の最適解は以下のように表されます。
\pi_k &= \frac{\sum_{n=1}^{N} r_{nk} }{\sum_{n=1}^{N} \sum_{k=1}^{K} r_{nk}} = \frac{N_k}{N}
\end{align}
ここまでをまとめます。
EMアルゴリズムのGMMへの適用(GMM-EM)は,以下の4ステップから構成される。
- 初期値設定
- 負担率$r_{nk}$と$\calQ$関数の計算(Eステップ)
- 各パラメータの更新(Mステップ)
- 収束判定
まずは各パラメータに初期値$\vmu_0$,$\mSigma_0$,$\pi_0$を与える。次に,以下のEステップとMステップを収束するまで繰り返す。
Eステップ
以下の負担率$r_{nk}$と$\calQ$関数を計算する。
r_{nk} &= \frac{\pi_k \N (\vx_n | \vmu_k, \mSigma_k)} {\sum_{j=1}^{K} \pi_j \N (\vx_n | \vmu_j, \mSigma_j)} \\[0.7em]
\calQ(\theta,\theta^{\old}) &= \sum_{n=1}^{N} \sum_{k=1}^{K} r_{nk} \left[-\frac{1}{2}\left\{ \ln |\mSigma_k|-(\vx_n-\vmu_k)^{T}\mSigma_k^{-1}(\vx_n-\vmu_k) \right\} \right]
\end{align}
Mステップ
$\calQ$関数を最大にするように以下のパラメータを計算する。
N_k &= \sum_{n=1}^{N} r_{nk} \\[0.7em]
\vmu_k &= \frac{\sum_{n=1}^{N} r_{nk} \vx_n}{N_k} \\[0.7em]
\mSigma_k &= \frac{\sum_{n=1}^{N} r_{nk} (\vx_n-\vmu_k)(\vx_n-\vmu_k)^T}{N_k} \\[0.7em]
\pi_k &= \frac{N_k}{N}
\end{align}
以上で,EMアルゴリズムのGMMへの適用は完了です。初期値の設定や収束判定は,実装の章で確認します。
実装
本章では,GMMを題材にEMアルゴリズムに基づくクラスタリングの実装をお伝えしていきます。具体的には,10000個の3次元データに対してGMM-EM(EMアルゴリズムによる混合ガウス分布の推論)を利用してクラスタリングする実装例をお伝えしていきます。要するに,以下のパラメータを仮定します。
N &= 10000 \\[0.7em]
D &= 3
\end{align}
実装はGithubで公開しています。
ソースコードのコメントは英語で書いています。これはGithubで公開する際に,外国の方々にも参考にしていただきたいからです。コメント規則であるdocstringはGoogleスタイルを利用しています。また,上記リポジトリには変分ベイズの実装も含まれています。
ここからは,以下の形式でメソッド単位で解説を行っていきます。
[メソッド名・その他タイトルなど]
# ソースコード[ソースコードの解説]
データの準備
以下では,GMM-EMを適用するデータを生成していきます。
import sys # 引数の操作
import csv # csvの読み込み
import numpy as np # 数値計算
import matplotlib.pyplot as plt # 可視化
from collections import Counter # 頻度カウント
from scipy.stats import multivariate_normal # 多次元ガウス分布の確率密度関数の計算
from mpl_toolkits.mplot3d import Axes3D # 可視化標準的なライブラリをインポートします。
# 各クラスターに属するデータ数
# 今回は全てのクラスタでデータ数が同じと仮定する
# 全体のデータ数は N = N1 + N2 + N3 + N4 となる
# 各クラスタのデータ数
N1 = 4000
N2 = 3000
N3 = 2000
N4 = 1000
# 平均
Mu1 = [5, -5, -5]
Mu2 = [-5, 5, 5]
Mu3 = [-5, -5, -5]
Mu4 = [5, 5, 5]
# 共分散
Sigma1 = [[1, 0, -0.25], [0, 1, 0], [-0.25, 0, 1]]
Sigma2 = [[1, 0, 0], [0, 1, -0.25], [0, -0.25, 1]]
Sigma3 = [[1, 0.25, 0], [0.25, 1, 0], [0, 0, 1]]
Sigma4 = [[1, 0, 0], [0, 1, 0], [0, 0, 1]]
# 乱数を生成
X1 = np.random.multivariate_normal(Mu1, Sigma1, N1)
X2 = np.random.multivariate_normal(Mu2, Sigma2, N2)
X3 = np.random.multivariate_normal(Mu3, Sigma3, N3)
X4 = np.random.multivariate_normal(Mu4, Sigma4, N4)データを作成します。今回は4つのガウス分布からデータを生成しましょう。クラスタリングとしては非常に簡単な問題設定になっています。なお,以下で載せている画像は当サイトのカラーリストを利用していますが,今回お伝えする実装はtab10のcolormapを利用します。本質的には重要でない部分ですので,気にしなくても大丈夫です。
# 描画準備
fig = plt.figure(figsize=(4, 4), dpi=300)
ax = Axes3D(fig)
# 当サイトのカスタムカラーリスト
cm = plt.get_cmap("tab10")
# メモリを除去
ax.set_xticks([])
ax.set_yticks([])
ax.set_zticks([])
# 少し回転させて見やすくする
ax.view_init(elev=10, azim=70)
# 描画
ax.plot(X1[:,0], X1[:,1], X1[:,2], "o", ms=0.5, color=cm(0))
ax.plot(X2[:,0], X2[:,1], X2[:,2], "o", ms=0.5, color=cm(1))
ax.plot(X3[:,0], X3[:,1], X3[:,2], "o", ms=0.5, color=cm(2))
ax.plot(X4[:,0], X4[:,1], X4[:,2], "o", ms=0.5, color=cm(3))
plt.show()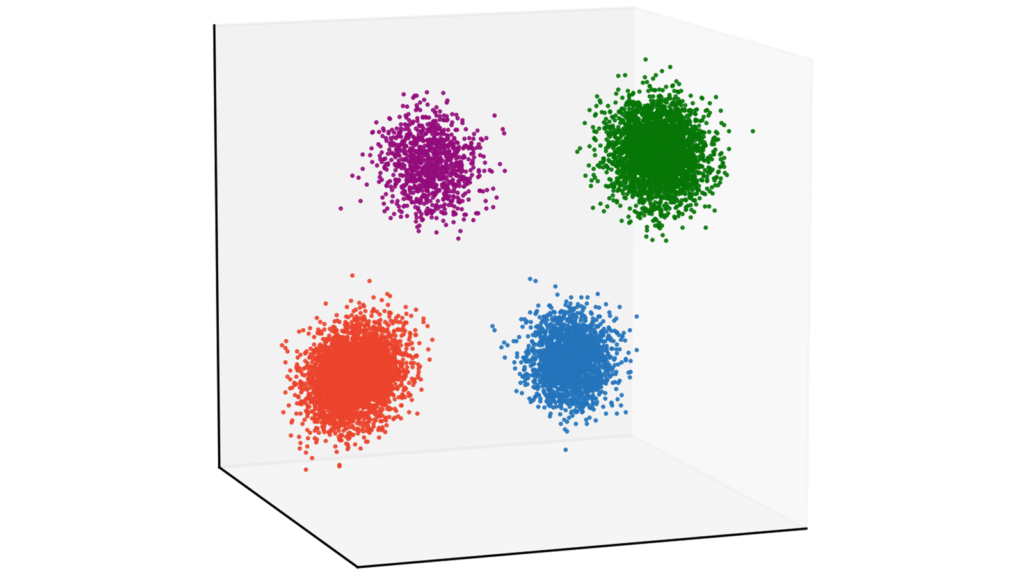
可視化して確認していきましょう。
# 4つのクラスを結合
X = np.concatenate([X1, X2, X3, X4])
# 描画準備
fig = plt.figure(figsize=(4, 4), dpi=300)
ax = Axes3D(fig)
# メモリを除去
ax.set_xticks([])
ax.set_yticks([])
ax.set_zticks([])
# 少し回転させて見やすくする
ax.view_init(elev=10, azim=70)
# 描画
ax.plot(X[:,0], X[:,1], X[:,2], "o", ms=0.5, color=cm(0))
plt.show()
今回は,4つのクラスラベルを排除したものをクラスタリング対象としますので,データを結合しましょう。
# csvでデータを保存
np.savetxt("data.csv", X, delimiter=",")毎回同じデータに対してクラスタリングを行うため,データをcsvに吐き出しておきます。当サイトのデモで利用しているcsvは以下でダウンロードできます。
# ご自身の環境におけるcsvへのパス
csv_dir = "[path to data.csv]"
# csvを読み取って(N, D)行列を生成
with open(csv_dir) as f:
reader = csv.reader(f)
X = [_ for _ in reader]
for i in range(len(X)):
for j in range(len(X[i])):
X[i][j] = float(X[i][j])
# 後のためにnumpy化しておく
X = np.array(X)当サイトと全く同じデータを利用したい場合は,上記ボタンからcsvをダウンロードしていただき,csvからデータを生成してください。ただし,[path to data.csv] にはご自身の環境におけるcsvファイルへのパスを挿入してください。
GMMEMクラスの定義
class GMMEM():ここからは,GMMEMクラスを定義していきます。
コンストラクタ
def __init__(self, K):
"""コンストラクタ
Args:
K (int): クラスタ数
Returns:
None.
Note:
eps (float): オーバーフローとアンダーフローを防ぐための微小量
"""
self.K = K
self.eps = np.spacing(1)クラスタ数Kと微小量epsを定義します。epsは$0$除算を防ぐため等に利用します。
パラメータ初期化メソッド
def init_params(self, X):
"""パラメータ初期化メソッド
Args:
X (numpy ndarray): (N, D)サイズの入力データ
Returns:
None.
"""
# 入力データ X のサイズは (N, D)
self.N, self.D = X.shape
# 平均は標準ガウス分布から生成
self.mu = np.random.randn(self.K, self.D)
# 分散共分散行列は単位行列
self.sigma = np.tile(np.eye(self.D), (self.K, 1, 1))
# 重みは一様分布から生成
self.pi = np.ones(self.K) / self.K
# 負担率は標準正規分布から生成するがEステップですぐ更新するので初期値自体には意味がない
self.r = np.random.randn(self.N, self.K)| 変数 | サイズ | 意味 |
N | int | データ数 |
D | int | データの次元 |
mu | (K, D) | ガウス分布の平均 |
sigma | (K, D, D) | ガウス分布の分散共分散行列 |
pi | (K) | ガウス分布の混合率 |
r | (N, K) | 負担率 |
パラメータの初期化を行います。ただし,rはEステップにおいて更新されますので,初期値自体には特に意味はありません。
GMMの確率密度関数計算メソッド
def gmm_pdf(self, X):
"""N個のD次元データに対してGMMの確率密度関数を計算するメソッド
Args:
X (numpy ndarray): (N, D)サイズの入力データ
Returns:
gmm_pdf (numpy ndarray): 各クラスタにおけるN個のデータに関して計算するため出力サイズは (N, K) となる
"""
return np.array([self.pi[k] * multivariate_normal.pdf(X, mean=self.mu[k], cov=self.sigma[k]) for k in range(self.K)]).T # (N, K)混合ガウス分布の確率密度関数を計算します。このメソッドは,対数尤度やEステップの計算で大活躍します。具体的には,以下を計算します。
\pi_k \N (\vx_n | \vmu_k, \mSigma_k)
\end{align}
多変量ガウス分布の確率密度関数の計算は,scipy.statsのmultivariate_normalというモジュールを利用します。
Eステップメソッド
def e_step(self, X):
"""Eステップを実行するメソッド
Args:
X (numpy ndarray): (N, D)サイズの入力データ
Returns:
None.
Note:
以下のフィールドが更新される
self.r (numpy ndarray): (N, K)サイズの負担率
"""
# GMMの確率密度関数を計算
gmm_pdf = self.gmm_pdf(X)
# 対数領域で負担率を計算
log_r = np.log(gmm_pdf) - np.log(np.sum(gmm_pdf, 1, keepdims=True) + self.eps)
# 対数領域から元に戻す
r = np.exp(log_r)
# np.expでオーバーフローを起こしている可能性があるためnanを置換しておく
r[np.isnan(r)] = 1.0 / (self.K)
# 更新
self.r = rEステップでは,以下の負担率を計算します。
r_{nk} &= \frac{\pi_k \N (\vx_n | \vmu_k, \mSigma_k)} {\sum_{j=1}^{K} \pi_j \N (\vx_n | \vmu_j, \mSigma_j)}
\end{align}
ここで,実装特有の注意点があります。ガウス分布の計算には指数計算が含まれるため,オーバーフローを引き起こす可能性があります。そこで,基本的には数値演算は対数領域で行うという鉄則があります。そこで,今回の負担率も対数領域で計算を行い,最後に対数領域から元に戻すという方法で計算していきます。
厳密に言えば,scipy.statsのmultivariate_normalはガウス分布の計算を対数領域で行っていませんので,オーバーフローのリスクを許容していると言えます。しかし,変分ベイズへの拡張という観点も含めて,今回は混合ガウス分布の確率密度が求められているものと仮定して,負担率から対数領域で計算していく方針を採用します。
早速,負担率の対数を取ってみましょう。
\ln r_{nk} &= \ln \frac{\pi_k \N (\vx_n | \vmu_k, \mSigma_k)} {\sum_{j=1}^{K} \pi_j \N (\vx_n | \vmu_j, \mSigma_j)} \\[0.7em]
&= \ln \pi_k \N (\vx_n | \vmu_k, \mSigma_k)-\left[\ln p(\mX|\pi_k, \vmu_k, \mSigma_k)\right]_n \label{em_log_r}
\end{align}
ただし,$[\cdot]_n$は行列の$n$インデックス目の要素を表し,対数尤度が以下で表されることを利用しました。
\ln p(\mX | \vpi, \vmu, \mSigma) &= \sum_{n=1}^{N} \ln \left\{ \sum_{j=1}^{K} \pi_j \N (\vx_n | \vmu_j, \mSigma_j) \right\}
\end{align}
式(\ref{em_log_r})の第一項目は,上で定義したgmm_pdf()メソッドが利用できます。式(\ref{em_log_r})の第二項目は,各データごとの対数尤度を表しており,こちらも上で定義したgmm_pdf()メソッドが利用できます。以下の対数尤度の計算は収束判定でも利用するので,このタイミングでおさえておくようにしましょう。
# 対数尤度の計算部分
np.log(np.sum(gmm_pdf, 1, keepdims=True) + self.eps)ただし,$\ln 0$演算を防ぐために微小量epsを加えている点に注意して下さい。
対数領域の負担率が計算できれば,あとはnp.exp()を通して元に戻してあげるだけです。その際,オーバーフローを起こしている可能性があるため,np.isnan()を利用して一様分布から生成された初期値に置換してあげましょう。
Mステップメソッド
def m_step(self, X):
"""Mステップを実行するメソッド
Args:
X (numpy ndarray): (N, D)サイズの入力データ
Returns:
None.
Note:
以下のフィールドが更新される
self.pi (numpy ndarray): (K) サイズの混合率
self.mu (numpy ndarray): (K, D) サイズの混合ガウス分布の平均
self.sigma (numpy ndarray): (K, D, D) サイズの混合ガウス分布の分散共分散行列
"""
# Q関数を最大にするパラメータ (mu, sigma, pi) を計算する
# まずは N_k を計算しておく
N_k = np.sum(self.r, 0) # (K)
# 最適なpiを計算して更新する
self.pi = N_k / self.N # (K)
# 最適なmuを計算して更新する
self.mu = (self.r.T @ X) / (N_k[:, None] + np.spacing(1)) # (K, D)
# 最適なsigmaを計算して更新する
r_tile = np.tile(self.r[:,:,None], (1, 1, self.D)).transpose(1, 2, 0) # (K, D, N)
res_error = np.tile(X[:,:,None], (1, 1, self.K)).transpose(2, 1, 0) - np.tile(self.mu[:,:,None], (1, 1, self.N)) # (K, D, N)
self.sigma = ((r_tile * res_error) @ res_error.transpose(0, 2, 1)) / (N_k[:,None,None] + np.spacing(1)) # (K, D, D)Mステップを実行します。具体的には,以下を計算します。
N_k &= \sum_{n=1}^{N} r_{nk} \\[0.7em]
\vmu_k &= \frac{\sum_{n=1}^{N} r_{nk} \vx_n}{N_k} \\[0.7em]
\mSigma_k &= \frac{\sum_{n=1}^{N} r_{nk} (\vx_n-\vmu_k)(\vx_n-\vmu_k)^T}{N_k} \\[0.7em]
\pi_k &= \frac{N_k}{N}
\end{align}
muとsigmaに関して,愚直にfor文を利用して各要素ごとに計算しても良いのですが,計算量が大きくなってしまいます。特にsigmaの計算は今回の設定では$O(KDN)=O(10^5)$となり,Pythonでは少し時間を要してしまいます。そこで,今回は演算子の一種である*と@を利用して行列計算を行います。
*はint同士の計算でも利用される積を表す演算子です。これをnumpy.ndarrayに適用すると,要素積(アダマール積)の演算子となります。
(i,j) * (i,j) = (i,j)
ただし,i,jは行列のサイズを表します。行列が3次元以上になっても同じです。
(i,j,k) * (i,j,k) = (i,j,k)
(i,j,k,l) * (i,j,k,l) = (i,j,k,l)
@はnumpy.matmulというモジュールの簡略化演算子であり,行列積を表します。*は行列が多次元になったときも対応する要素同士の積を計算するだけですが,@は少し注意が必要です。行列積は2次元の行列に対して定義されますので,3次元以上の行列に対して@を取るときは,numpyでは後ろの2次元以外の軸はバッチ数とみなしてくれるのです。
うまく想像できない方が多いと思います。例を挙げましょう。単純に,2次元の行列に対して@を適用する場合は,
(i,j) @ (j,k) -> (i,k)
という演算になります。一方で,3次元の行列に対して@を適用する場合は,
(b,i,j) @ (b,j,k) -> (b,i,k)
のように,一番左の軸をバッチ数とみなして保ってくれるのです。逆に言うと,一番左の軸が異なる値で設定されていると,@は機能しません。4次元以上も同様で,右2つの軸で行列積を取って他の軸はそのまま保ってくれます。
(b1,b2,i,j) @ (b1,b2,j,k) -> (b1,b2,i,k)
本実装では,行列のサイズを調整するためにnp.tileというモジュールを利用しています。例えば(A,B)サイズの行列に対してnp.tileの引数で(a,b)を指定すると,出力サイズは(aA,bB)となります。
np.tile((A,B), (a,b)) -> (aA,bB)
引数に渡す行列のサイズと指定する積み重ね方のサイズは合致していなくても良いのですが,混乱を防ぐため,ここではスライスで積み重ねたい方向の軸にNoneを指定することによって積み重ねたい軸をあらかじめ拡張しておく方針をとります。
さて,話を元に戻します。muに関しては,データ数$N$方向に関して総和をとりたいため,$N$方向の軸に関して行列積@を取ればよいです。$N$方向の行列積は,$N$方向の総和になるからです。
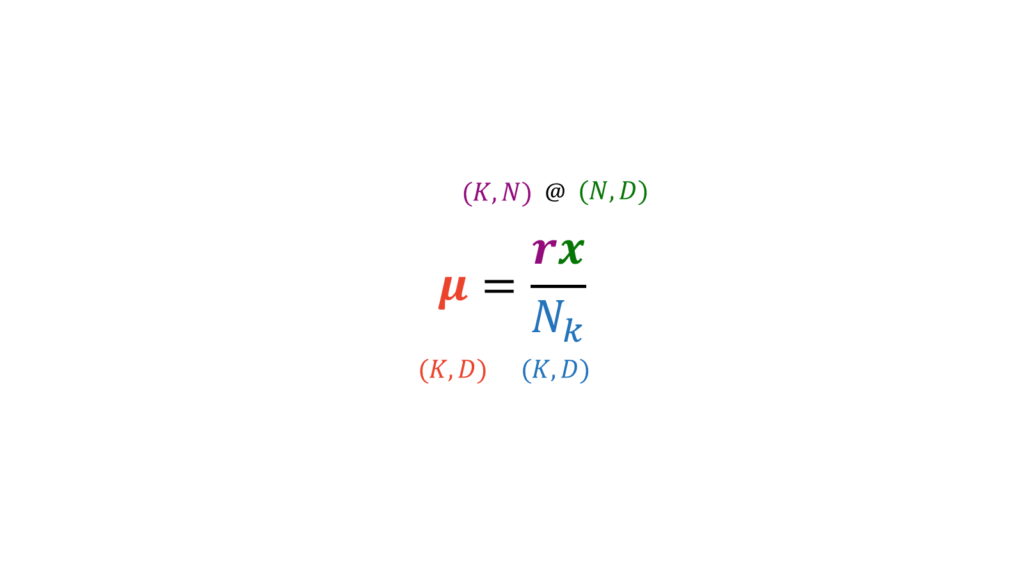
sigmaに関しては,要素積*と行列積@をうまく組み合わせて計算します。
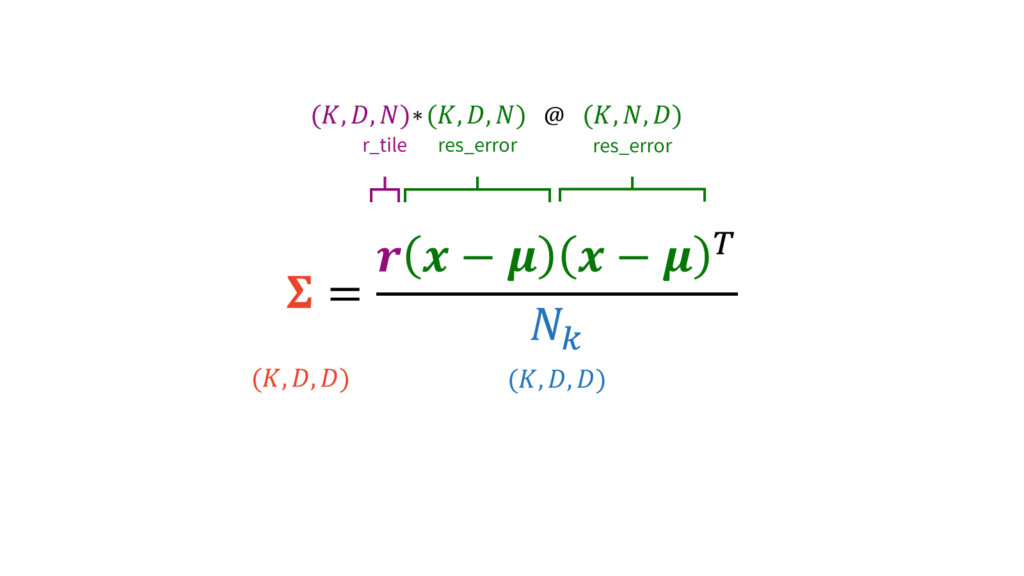
numpyには以上の操作を明示的に行うnp.einsumというモジュールが用意されています。使い方はシンプルです。添え字を使って,行列演算を行いたい軸を指定します。例えば,
(ijk, ikl -> ijl)
などと指定してあげれば,i軸方向の次元は保ったまま
(j,k) @ (k,l) = (j,l)
という行列積計算を行ってくれます。添え字はaやbなど他のアルファベットを利用しても大丈夫です。他にも,
(ijk, ijk -> ijk)
などと指定してあげれば,
(i,j,k) * (i,j,k) = (i,j,k)
という要素積(アダマール積)を取ることも可能です。
Pythonでは数学のテンソルとは別の概念で多次元行列をテンソルと呼ぶので注意です。本稿では,読者の混乱を防ぐため,テンソルという用語は使用していません。
可視化メソッド
def visualize(self, X):
"""可視化を実行するメソッド
Args:
X (numpy ndarray): (N, D)サイズの入力データ
Returns:
None.
Note:
このメソッドでは plt.show が実行されるが plt.close() は実行されない
"""
# クラスタリングを実行
labels = np.argmax(self.r, 1) # (N)
# 利用するカラーを極力揃えるためクラスタを出現頻度の降順に並び替える
label_frequency_desc = [l[0] for l in Counter(labels).most_common()] # (K)
# tab10 カラーマップを利用
cm = plt.get_cmap("tab10")
# 描画準備
fig = plt.figure(figsize=(4, 4), dpi=300)
ax = Axes3D(fig)
# メモリを除去
ax.set_xticks([])
ax.set_yticks([])
ax.set_zticks([])
# 少し回転させて見やすくする
ax.view_init(elev=10, azim=70)
# 各クラスタごとに可視化を実行する
for k in range(len(label_frequency_desc)):
cluster_indexes = np.where(labels==label_frequency_desc[k])[0]
ax.plot(X[cluster_indexes, 0], X[cluster_indexes, 1], X[cluster_indexes, 2], "o", ms=0.5, color=cm(k))
plt.show()EMアルゴリズムが収束した後に,各クラスごとに色分けした可視化を行い結果を確認します。
実行メソッド
def execute(self, X, iter_max, thr):
"""EMアルゴリズムを実行するメソッド
Args:
X (numpy ndarray): (N, D)サイズの入力データ
iter_max (int): 最大更新回数
thr (float): 更新停止の閾値 (対数尤度の増加幅)
Returns:
None.
"""
# パラメータ初期化
self.init_params(X)
# 各イテレーションの対数尤度を記録するためのリスト
log_likelihood_list = []
# 対数尤度の初期値を計算
log_likelihood_list.append(np.mean(np.log(np.sum(self.gmm_pdf(X), 1) + self.eps)))
# 更新開始
for i in range(iter_max):
# Eステップの実行
self.e_step(X)
# Mステップの実行
self.m_step(X)
# 今回のイテレーションの対数尤度を記録する
log_likelihood_list.append(np.mean(np.log(np.sum(self.gmm_pdf(X), 1) + self.eps)))
# 前回の対数尤度からの増加幅を出力する
print("Log-likelihood gap: " + str(round(np.abs(log_likelihood_list[i] - log_likelihood_list[i+1]), 2)))
# もし収束条件を満たした場合,もしくは最大更新回数に到達した場合は更新停止して可視化を行う
if (np.abs(log_likelihood_list[i] - log_likelihood_list[i+1]) < thr) or (i == iter_max - 1):
print(f"EM algorithm has stopped after {i + 1} iteraions.")
self.visualize(X)
break今まで定義してきたメソッドを駆使して,GMM-EMを実行します。初期化,Eステップ,Mステップ,収束判定と繰り返すことで,パラメータを更新していきます。収束判定では,「閾値」もしくは「最大更新回数」のいずれかが引っかかった場合に更新をストップするようにしています。
なお,閾値判定に用いる対数尤度は,全てのデータ点の和ではなく平均を利用しています。これは,データ点のスケールに閾値の大小が影響されないようにするためです。例えば,閾値判定に全てのデータ点の対数尤度の和を用いてしまうと,$N=10$と$N=10000$で用いる閾値のスケールが変わってしまい,実用上不便になってしまいます。
GMMEMの実行
上で定義したGMMEMクラスのインスタンスを生成して,GMM-EMを実行しましょう。以下では,GMM-VBとの比較を行うためにいくつかの条件で実行してみます。
$K=4$の場合
# モデルをインスタンス化する
model = GMMEM(K=4)
# EMアルゴリズムを実行する
model.execute(X, iter_max=100, thr=0.001)クラスタ数$K$は$4$,最大更新回数は$100$回としました。収束判定における対数尤度増加幅の閾値は$0.001$としました。

しっかりとクラスタリングできていますね。ログを確認すると,更新回数は$10$回だったことが分かります。
Log-likelihood gap: 19.66
Log-likelihood gap: 11.95
Log-likelihood gap: 4.53
Log-likelihood gap: 0.04
Log-likelihood gap: 0.74
Log-likelihood gap: 0.57
Log-likelihood gap: 0.01
Log-likelihood gap: 2.94
Log-likelihood gap: 1.65
Log-likelihood gap: 0.0
EM algorithm has stopped after 10 iteraions.$K=8$の場合
# モデルをインスタンス化する
model = GMMEM(K=8)
# EMアルゴリズムを実行する
model.execute(X, iter_max=100, thr=0.001)クラスタ数$K$は$8$として,他のパラメータは先ほどと同様の設定で行いました。
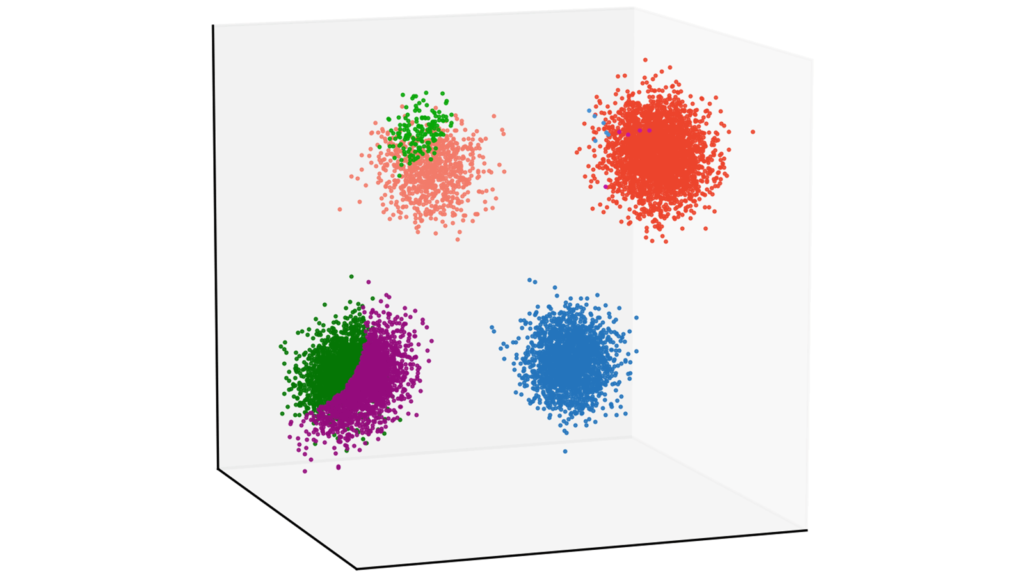
正しくクラスタリングされませんでした。ログを確認すると,更新回数は最大の$100$回となっていたため,うまく収束できなかったようです。点推定では,$4$つに分かれているクラスタを$K=8$の条件下では正しく推定できなかったということです。
Log-likelihood gap: 23.37
Log-likelihood gap: 8.06
Log-likelihood gap: 2.36
Log-likelihood gap: 3.5
Log-likelihood gap: 3.02
~~~~~~~~~~
省略
~~~~~~~~~~
Log-likelihood gap: 0.22
Log-likelihood gap: 0.2
Log-likelihood gap: 0.19
Log-likelihood gap: 0.18
Log-likelihood gap: 0.17
EM algorithm has stopped after 100 iteraions.データの中に実質的な情報が僅かしか含まれていない性質のことを「スパース性」と呼びます。今回の場合は,仮定したクラス数よりも実際に推定するクラス数の方が少なく,EMアルゴリズムがスパース性を考慮できなかったために,クラスラベルを正しく推定することができなかったと考えられます。変分ベイズでは,「関連度自動決定」という性質により,スパース性を担保したクラスタリングが可能になります [1]。
おわりに
本稿では,EMアルゴリズムの目的とその実現方法をボトムアップ的にお伝えしてきました。本稿が,一人でも多くの人にとってEMを学ぶ助けとなれることを心から願っております。
[1] Christopher M. Bishop, "Pattern Recognition and Machine Learning."


コメント
コメント一覧 (41件)
大変参考になる記事をありがとうございます。
ところで、(27), (28)のln p(Z)は、正しくはln q(Z)かと思われます。
Naoki さま
ご指摘誠にありがとうございます!
こちら修正完了しました。非常に助かりましたmm
一連の流れが丁寧に解説されており,非常に有益でした.心より感謝申し上げます.
一点質問させていただきたいのですが,(60)から(61)への式変形では,(56),(57)式を代入していると思いますが,このとき,(56)(57)の両方にπ_k^znkがあります.znkでくくった場合,π_kが2乗になりそうな気がしたのですが,こちらの解釈ミスであれば指摘いただければ幸いです.
私自身,数学や統計はめっぽう苦手で,こうした有益な記事を参考にしながら手探りで勉強している状態でして,こちらの見当違いでしたら申し訳ありません.
hoge さま
ご質問ありがとうございます。
このような場合は,一旦簡単な例に立ち戻ってみると分かりやすいです!
以下のような例を考えてみましょう。
例:$a=2^{3}$,$b=3^{3}$に対し$ab=x^{3}$とするとき,$x$は何になるか
答:
\begin{align}
ab=2^{3}\cdot 3^{3}=(2\cdot 3)^{3}=6^{3}
\end{align}
より,$x=6$となります。実際,$ab=8\cdot 27=216$となり,$6^{3}$と一致します。これは,以下の指数法則に基づきます。
\begin{align}
(ab)^{m} &= a^{m}b^{m}
\end{align}
ですので,$\pi_{k}$が二乗になることはないかと思います。
ありがたく勉強させていただいてます。
イェンゼンの不等式(20)の日本語説明文で、係数λの合計が1という記述が漏れています(Σしかない)。
修正お願いいたします。
のま さま
ご指摘誠にありがとうとざいます!
修正致しましたmm
不勉強で間違っている可能性がありますが、式57がsumになっているため、1を超えてしまう気がします。prodではないでしょうか?
ほげ 様
ご指摘誠にありがとうございます。
おっしゃる通り誤植でしたので,本文を修正致しました。
丁寧な解説で非常にわかりやすく、大変参考になっております。
記事の掲載非常にありがとうございます。
何点か質問をさせていただきたく。
私自身最近になって機械学習の勉強を始めた初学者であるため、記事を理解する上で基本的な知識が欠損しているかもしれません。
その際は参考文献を掲載していただけると助かります
①式(36)→式(37)の変形ですが、Q関数=ΣP(Z|X,θold)×lnP(X,Z|θ)という認識で間違いありませんか?
②式’(37)式の下にある文章の“対数尤度関数の潜在変数に関する期待値”とはΣZ×lnP(X,Z|θ)という認識で間違いありませんか?
―>“期待値“は”確率変数値“×”各確率変数が出る確率“の総和と認識しています(この認識が間違っていればご指摘をください)
③もし①&②がYESの場合、P(Z|X,θold)→Zになったという認識なのですが・・なぜこのようになるのでしょうか?
O_ha 様
ご指摘誠にありがとうございます。①&②がYESであり,本文が誤っておりました。潜在変数に関する期待値ではなく,正しくは潜在変数の事後分布に対する期待値でした。本文を修正しましたので,お手数ですがご確認ください。
私には非常に難解なトピックですが、ご丁寧に説明くださっているおかげで、なんとか一行一行ついていける気がしております。
細かい部分かつ私の理解不足で恐縮なのですが、Mステップで∑に関する勾配を求める際、式(80)から式(81)を導出する際に公式(83)を使用していると思いますが、(83)左辺のd/dxはd/dAではないのでしょうか?
やみくも 様
ご連絡ありがとうございます。ご指摘の通りでございますので、本文を修正致しました。また何かご質問があればお気軽にコメントください。
(54)の前の段落
「X = {x_1, ... , x_n}」
→「X = {x_1, ... , x_N}」が正しい。
(56)
p(0)=1となりおかしいです。
この書き方は総乗の中に入っているときにしか成立しませんし、それだけ言えても(57)や(61)の形式には直接結び付きません。
(58)からの式や(65)からの式も含めて、より厳密な方向に説明の仕方を変えるべきだと思います。
(62)
θとθ^{old}が区別されていません。
このままだとr_{nk}はθに依存することになり、ラグランジュの未定乗数法の微分の対象となります。
(64)
比例ではありませんし、{}内の符号は+が正しいです。
符号の反転は(81)まで続きます。
(65)
総和の中のkと外のkが区別されていません。
(77)
Aが対称行列でなければ成り立ちません。
(85)と(86)の間
「Σr_{nk}とおきました。」
→正しくは「N_k ≡ Σr_{nk}とおきました。」など正しい。
a 様
ご丁寧なご指摘,誠に恐れ入ります。本文を修正致しました。
>(64)
>比例ではありませんし、{}内の符号は+が正しいです。
>符号の反転は(81)まで続きます。
こちらですが,$\calQ$関数の途中式が間違えていたため,{}内の符号は-のままとなる認識です。
また,多変量正規分布の定数部分を無視しているため,比例となる認識です。
>Q関数の途中式が間違えていたため,{}内の符号は-のままとなる認識です。
正規分布の係数部|Σ|^(-1/2)と指数関数部exp(-1/2*…)からそれぞれ-1/2が出てくるので、-1/2で括ったら{}内は+だと思います。
仮に-のままが正しいとすれば(81)から導かれた(84)は全体に-がつくはずですよね?
同じ指摘の繰り返しになりますが、多変量正規分布の定数部分がlogにより加算で外に出るので比例にはなりません。
そもそも正規分布の係数部だけでなくπ_kの項も無視していますし。
π_kが無視されているのはまた別の問題でしたね。
符号が反転している話とは別で、πもθに含まれるので(64), (69), (74)ではlog(π_k)の項が残っていなければなりません。
a 様
ご指摘誠にありがとうございます。お恥ずかしい誤植でした。$\calQ$関数の計算以降を修正しました。
画期的に分かりやすい記事と丁寧な実装をどうも有難うございます!
文の理解には差し支えない些細な点を発見しましたので、お知らせします。よろしくお願いします。
[1] (64)及びその後:N \ln 2\pi -> D \ln 2\pi (多変量正規分布の正規化がデータ数Nではなく次元Dに依存)
[2] (67)の下の文:ただし,式(66)から式(66)への変形には ー> ただし,式(66)から式(67)への変形には
TO様
ご指摘誠にありがとうございます![1]と[2]のいずれについても修正致しました。コメント非常に助かりますmm
イェンゼンの不等式の呼び方について質問があります。
「これなら分かる最適化数学」という本の中だとイェンセンの不等式と書かれているのですが、なぜこのような表記ゆれがあるのでしょうか。「イェンセン」か「イェンゼン」かどっちでもいいと言われればそうなのですが、少し気になったので質問させていただきました。どちらの呼び方がより一般的か教えていただけると幸いです。
ご質問ありがとうございます。
人物固有名詞の発音は国によって異なるため,正解のカタカタ発音というのは存在しません。一方,Yensenがデンマーク出身の数学者であることを踏まえ,デンマーク人のJensenの発音を調べてみたところ(公式ソースではない),「イェンセン」という発音が正しそうです。ドイツ語では「イェンゼン」と濁ることがあるため,イェンゼンとカタカナ発音で表記されることがある模様です。当サイトにおいては,表記の一貫性を保つため,全ての記事で「イェンセン」と修正致しました。
本文と関係ないのですが、みんな初学者のフリしてマサカリ投げてきてるのに笑いました。
自分も「チョットワカル」っていいながらマサカリ投げられるように精進したいと思いました
ななし様
多くの方がしっかりと記事を読んだ上でコメントされているので、自分も勉強になっています。何かマサカリがあればお待ちしています!
大変勉強になっております.ありがとうございます.
すでに指摘があるかもしれませんが,式(20)の条件lambda_iの和の=1という条件が落ちているように思います.
Tomoyuki様
ご指摘誠にありがとうございます。本文を修正致しました。
式(50)で、事後確率p(Z|X,θold)を求めるとありますが、どのように求めるのでしょうか、、、?
例えば、p(X,θold)のようなものであれば、正規分布か何かのパラメータθを設定し、観測値Xを入れてあげれば求められると思いますが、潜在変数Zも絡んできているので、どのようにp(Z|X,θold)を求めればいいのか混乱しております、、、
混合ガウス分布のあたりは追いきれていませんが、ご回答頂けますと幸いです。
Yu様
ご質問ありがとうございます。式(59)〜式(61)の変形を見ると分かりやすいです。条件付き確率の定義を用いることで,事後確率に比例する値を計算できるようにしています。
(58)はp(X,Z|θ)=p(Z|θ)p(X|Z,θ)だと思います。
{p(X,Z)=p(X|Z)p(Z)から、分母にθをつけて(X,Z|θ)=p(Z|θ)p(X|Z,θ)}
p(Z)=p(Z|θ)と解釈して問題ないですか?
kim様
ご質問ありがとうございます。
>p(Z)=p(Z|θ)と解釈して問題ないですか?
定義が正確ではありませんでした。式(56)および式(58)を修正しましたので,ご確認いただけますでしょうか。
Zuca様
ご回答ありがとうございます。
式(59)-(61)のあたり、把握しました。
また、質問させていただきたいのですが、式(50)の左辺のXはxnの間違いでしょうか?
また、式(66)-(67)の式変換で、分母の、znjに関する中括弧{}が外れておりますが、こちらはなぜでしょうか、、、?
見当違いなことをお伺いしていたら申し訳ありません
Yu様
ご質問ありがとうございます。
>式(50)の左辺のXはxnの間違いでしょうか?
式(50)の左辺に$X$が登場していないのですが,再度式番号をご確認いただけますでしょうか。
>式(66)-(67)の式変換
こちらに関して,誤植がありましたので訂正しました。修正後の式変形で不明な箇所があればご指摘ください。
zuka様
>式(50)の左辺にが登場していないのですが,再度式番号をご確認いただけますでしょうか。
もうわけありません。
式(54)の間違いでした、、、
p(X|π, μ, Σ)ではなくp(xn|π, μ, Σ)なのかと考えておりました。
また、該当箇所の式を修正いただき、ありがとうございます。
式変形を追うことができました。
Yu様
ご質問ありがとうございます。
>p(X|π, μ, Σ)ではなくp(xn|π, μ, Σ)なのかと考えておりました。
ご指摘の通りです。本文を修正しました。
度々申し訳ありません。
式(56)において、右辺に、μ、Σが無いにも関わらず、左辺がp(Z|Θ)となっています。
π、μ、Σをまとめて、Θとする記述がありますが、π、μ、Σどれか一つしかなくても、Θと表現することができる認識でしょうか、、、?
追加で質問させてください。
式(59)の右辺の分母は、P(X)ではなく、P(X|θ)でしょうか?
3つの確率変数のベイズの定理、および条件付き確率の連鎖率を用いてP(Z|X)を計算したところ、分母が、P(X|θ)となりました、、、
Yu様
>π、μ、Σどれか一つしかなくても、Θと表現することができる認識でしょうか、、、?
はい,認識通りです。変文推論と表記を揃えつつ,表記の簡単のため,曖昧な表記にしております。ただ,今振り返るとやや分かりにくく感じていますので,どこかのタイミングで改善したいと考えています。
>式(59)の右辺の分母は、P(X)ではなく、P(X|θ)でしょうか?
ご指摘ありがとうございます。おっしゃる通りですので,本文を修正致しました。
zuka様
確認が遅くなり、申し訳ありません。
一つ一つ回答いただき、ありがとうございます。
おかげさまで理解が深まりました。
”混合ガウス分布への適用”のセクションで誤植を見つけたので報告させていただきます。
【原文】z_nは,one-hot-vector(ある要素だけで他は0となるベクトル)
【訂正文】z_nは,one-hot-vector(ある要素だけ1で他は0となるベクトル)
maru様
ご指摘誠にありがとうございます。本文を修正致しました。
大変わかりやすく勉強になりました。
一点、イエンセンの不等式は、不等式の向きが逆でないでしょうか。
イエンセンの不等式の向きが逆でも(正しい方でも)平均を関数と扱うことで、同じ結論になると思います。
tm様
ご指摘ありがとうございます。今回イェンセンの不等式を適用している関数は上に凸ですので、不等式の向きは合っているように思えるのですが、いかがでしょうか。