本記事は「これなら分かる!はじめての数理統計学」シリーズに含まれます。
不適切な内容があれば,記事下のコメント欄またはお問い合わせフォームよりご連絡下さい。
負の二項分布
f_{X}(x) &= {}_{r+x-1} C_{x}\;p^{r}q^{x} = {}_{-r} C_{x}\;p^{r} (-q)^{x} \\[0.7em]
G_{X}(s) &= \left(\frac{p}{1-qs} \right)^{r} \\[0.7em]
E[X] &= r\frac{q}{p} \\[0.7em]
V[X] &= r \frac{q}{p^2}
\end{align}
無限に続くベルヌーイ試行において,$r$回成功するまでの失敗の回数$X$は,負の二項分布
\NB (r, p)
\end{align}
に従います。ただし,$r \in \mN$,$p \in [0, 1]$とし,$q=1-p$とおきました。負の二項分布に従う確率変数$X$に対し,実現値は
x \in \{0, 1, \ldots \}
\end{align}
であり,確率母関数の変数は$|s|\leq 1$とします。負の二項分布は再生性を持ち,ロードマップ中では負の二項分布は二項分布の極限に相当します。なお,負の二項分布はポアソン分布の混合分布としても定義されます。
確率密度関数
負の二項分布は「$r$回表が出るまでの失敗の回数」を確率変数とする確率分布です。この定義から,確率密度関数は自然に導かれます。
f_{X}(x) &= {}_{r+x-1} C_{x}\;p^{r}q^{x}
\end{align}
ここで,負の二項係数を定義しましょう。二項係数の定義の自然な拡張として,負の二項係数は$(1+t)^{-r}$の$t^{x}$の係数として定義され,${}_{-r} C_{x}$と表されます。
(1+t)^{-r} &= \sum_{x=0}^{\infty}{}_{-r} C_{x} t^{x}\label{負の二項係数の定義}
\end{align}
式($\ref{負の二項係数の定義}$)の左辺を$g(t)$とおくと,$g$の$x$階微分は
g^{(x)}(t)
&= (-r)(-r-1)\cdots (-r-x+1)(1+t)^{-r-x}\\[0.7em]
&= (-1)^{x}r(r+1)\cdots(r+x-1)(1+t)^{-r-x}\\[0.7em]
&= (-1)^{x}(r+x-1)(r+x-2)\cdots r(1+t)^{-r-x}\\[0.7em]
&= (-1)^{x}\frac{(r+x-1)!}{(r-1)!}(1+t)^{-r-x}
\end{align}
となります。したがって,$g$のマクローリン展開は
(1+t)^{-r}
&= \sum_{x=0}^{\infty}\frac{g^{(x)}(0)}{x!}t^{x}\\[0.7em]
&= \sum_{x=0}^{\infty}(-1)^{x}\frac{(r+x-1)!}{x!(r-1)!}t^{x}\\[0.7em]
&= \sum_{x=0}^{\infty}(-1)^{x}\frac{(r+x-1)!}{x!(r-1)!}t^{x}
\end{align}
となります。$t^{x}$の係数が負の二項係数の定義でしたので,
{}_{-r} C_{x} &= (-1)^{x}\frac{(r+x-1)!}{x!(r-1)!}
\end{align}
が得られました。この定義を用いれば,負の二項分布の確率質量関数は
f_{X}(x)
&= {}_{r+x-1} C_{x}\;p^r (1-p)^{x}\\[0.7em]
&= \frac{(r+x-1)!}{x!(r-1)!}\;p^r q^{x}\\[0.7em]
&= (-1)^{x}\frac{(r+x-1)!}{x!(r-1)!}\;p^r (-q)^{x}\\[0.7em]
&= {}_{-r} C_{x}\;p^r (-q)^{x}
\end{align}
とも表されることが分かります。
確率母関数
先ほど導入した負の二項係数の定義に注意すると,負の二項分布の確率母関数は
E[s^x]
&= \sum_{x=0}^{\infty} s^x {}_{-r}\C_{x}p^{r}(-q)^{x}\\[0.7em]
&= p^{r}\sum_{x=0}^{\infty} {}_{-r}\C_{x}(-qs)^{x}\\[0.7em]
&= p^{r}(1-qs)^{-r}\\[0.7em]
&= \left(\frac{p}{1-qs}\right)^{r}
\end{align}
となります。
補足
負の二項分布の確率母関数を求める別解として「$r$回表が出るまでの失敗の回数」を「$1$回表が出るまでの失敗の回数の和」と捉える方法があります。つまり,幾何分布に従う$r$個の独立な確率変数$X_1,\cdots,X_r$の和$S$が負の二項分布に従います。
G_{S}(s) &= G_{X_1+\cdots+X_r}(s) \\[0.7em]
&= G_{X_1}(s)\cdots G_{X_r}(s)\\[0.7em]
&= \left\{ \frac{p}{1-qs} \right\}^r
\end{align}
平均・分散
離散分布の平均と分散を求めるためには,確率母関数の性質を利用します。
E[S_r] &= E[X_1 + \cdots + X_r]\\[0.7em]
&= E[X_1] + \cdots + E[X_r]\\[0.7em]
&= r\frac{1-p}{p}\\[0.7em]
V[S] &= V[X_1 + \cdots + X_r]\\[0.7em]
&= V[X_1] + \cdots + V[X_r]\\[0.7em]
&= r\frac{1-p}{p^2}\\[0.7em]
\end{align}
ただし,分散の計算では$X_1, \ldots, X_r$がそれぞれ互いに独立であることを利用しました。
補足
負の二項分布がポアソン分布とガンマ分布の混合から得られることからも,平均と分散を求めることができます。いま,$X|\Lambda{\sim}\Po(\lambda)$および$\Lambda{\sim}\Gamma(\alpha,\beta)$とおくと,ポアソン分布の平均と分散より$E[X|\Lambda]{=}V[X|\Lambda]{=}\lambda$となり,ガンマ分布の平均と分散より$E[\Lambda]{=}\alpha/\beta$および$V[\Lambda]{=}\alpha/\beta^{2}$となります。したがって,条件付き期待値・分散の性質を利用すると,
\begin{cases}
\displaystyle
E_{X}[X] = E_{\Lambda}[E_{X|\Lambda}[X|\Lambda]] = E_{\Lambda}[\Lambda] = \frac{\alpha}{\beta}\\[0.7em]
\displaystyle
V_{X}[X] = E_{\Lambda}[V_{X|\Lambda}[X|\Lambda]]+V_{\Lambda}[E_{X|\Lambda}[X|\Lambda]]
= E_{\Lambda}[\Lambda]+V_{\Lambda}[\Lambda]
= \frac{\alpha}{\beta}\left(1+\frac{1}{\beta}\right)
\end{cases}
\end{align}
となります。恣意的ですが,$\alpha{=}r$および$\beta/(\beta+1){=}p$とおくと,負の二項分布の平均と分散が求められます。
再生性
再生性を示すためには,再生性を示したい分布に従う独立な二つの確率変数を考え,その和の確率母関数を計算したときに,パラメータが和の形になっていることを示します。いま,二つの独立な確率変数
X &\sim \NB (r_{x}, p) \\[0.7em]
Y &\sim \NB (r_{y}, q)
\end{align}
を考えます。 このとき,$X+Y$の確率母関数を計算します。
G_{X+Y}(s)
&=G_{X}(s)G_{Y}(s)\\[0.7em]
&= \left(\frac{p}{1-qs}\right)^{r_{x}}\left(\frac{p}{1-qs}\right)^{r_{y}}\\[0.7em]
&= \left(\frac{p}{1-qs}\right)^{r_{x}+r_{y}}
\end{align}
これは,$X+Y$の確率母関数が$\NB(r_{x}+r_{y},p)$の確率母関数であることを示しています。つまり,
X+Y &\sim \NB(r_{x}+r_{y},p)
\end{align}
であり,負の二項分布の再生性を示しています。
ロードマップ
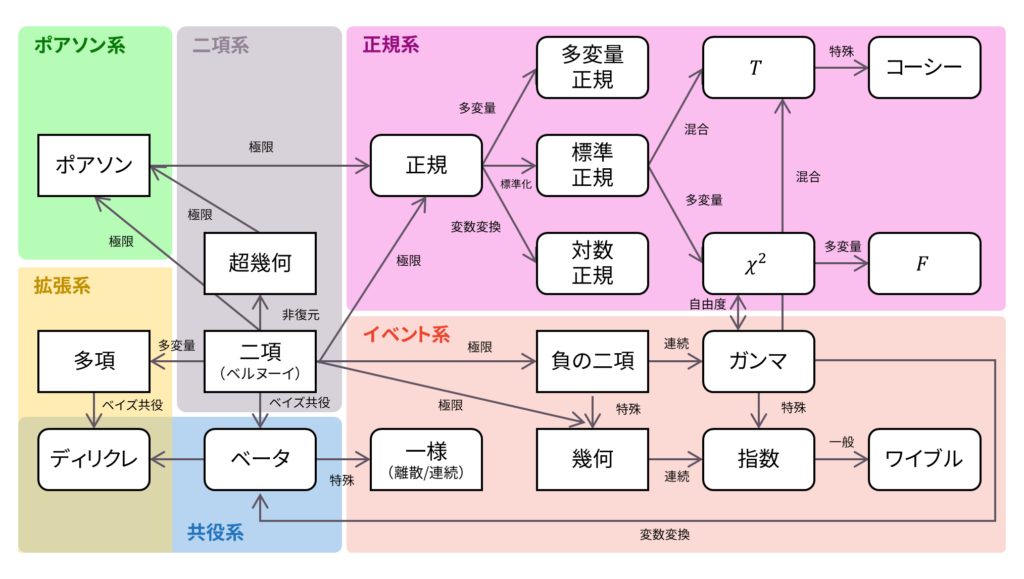
さて,ロードマップに戻りましょう。 負の二項定理は二項定理を一般に拡張したテイラー級数を利用して母関数が求められました。また,幾何分布に従う確率変数の和としても定義できました。逆に言えば,負の二項分布において,$r=1$という特殊な場合が幾何分布に相当するということになります。以下の内容も参考になるでしょう。
参考文献
本稿の執筆にあたり参考にした文献は,以下でリストアップしております。


コメント