本記事は「これなら分かる!はじめての数理統計学」シリーズに含まれます。
不適切な内容があれば,記事下のコメント欄またはお問い合わせフォームよりご連絡下さい。
M/M/1モデルの待ち行列理論
平均到着率を$\lambda>0$,平均サービス率を$\mu>0$と置く。十分時間が経過したとき,M/M/1モデルの平均待ち行列長は
\frac{\rho}{1-\rho} \label{平均待ち行列長}
\end{align}
で表され,平均待ち時間は
\frac{\rho}{1-\rho} \cdot \frac{1}{\mu} \label{平均待ち時間}
\end{align}
で表される。ただし,$\rho=\lambda/\mu$と置いた。
証明
M/M/1モデル
M/M/1モデルはケンドールの記号と呼ばれる表現方法で,
[到着発生の仮定]/[サービス提供の仮定]/[窓口の数]
を表します。MというのはMarkov processの頭文字で,マルコフ過程を意味しています。マルコフ過程というのは,マルコフ性をもつ確率過程を指します。マルコフ性というのは,確率過程において未来の挙動が現在の値だけで決定される性質を指し,無記憶性とも呼ばれています。確率過程というのは,語弊を恐れずに言うならば,時間変動を組み入れた確率分布です。差し当たりは,確率過程と確率分布は似たようなものだと把握しておけば問題ありません。
本稿では,これ以降はマルコフ性を無記憶性と呼ぶことにします。
したがって,M/M/1モデルというのは
- 到着の発生:無記憶性を持つ
- サービスの提供:無記憶性を持つ
- サービスの窓口:1個
を仮定する待ち行列理論になります。さて,まずは到着という事象の時間間隔について着目してみましょう。無記憶性を持つ連続型確率分布は指数分布のみですので,到着の時間間隔は指数分布に従うことが分かります。同様に,サービスの時間間隔も指数分布に従うことが分かります。
さらに,指数分布の導出方法を参考にすると,事象の発生回数がポアソン分布に従うときに時間間隔は指数分布に従うことが分かります。すなわち,到着の時間間隔が指数分布に従うとき,到着の発生回数はポアソン分布に従います。同様に,サービスの提供回数はポアソン分布に従います。したがって,M/M/1モデルというのは,以下を仮定する待ち行列理論になります。
- 到着の時間間隔:指数分布
- 到着の回数:ポアソン分布
- サービスの時間間隔:指数分布
- サービスの回数:ポアソン分布
- サービスの窓口:1個
平均待ち行列長と平均待ち時間
平均待ち行列長の導出では,定常過程における待ち行列長が幾何分布に従うことを利用します。冒頭でもお伝えした通り,本稿では漸近理論に踏み入れませんので,待ち行列長が定常過程に漸近するという過程のもと議論を進めていきます。
定常過程とは,ざっくり「十分時間が経って収束した場合の確率過程(分布)」と捉えておけばよいでしょう。
方針は大きく以下の三つに分かれます。定常分布のつりあいを利用する方法と微分方程式を利用する方法は,本質的には等価になります。というのも,微分方程式を用いた方針においては,定常性の仮定を行うことで定常分布のつりあいの条件式が導かれるという流れになっています。
- 大雑把に無記憶性を仮定
- 定常分布のつりあいを利用
- 微分方程式を利用
大雑把に無記憶性を仮定
M/M/1モデルは,到着の時間間隔とサービスの時間間隔という連続型の確率変数に関して無記憶性を仮定しました。これを大雑把に発展させます。到着とサービスに無記憶性を仮定するのであれば,定常過程における待ち行列長にも無記憶性が仮定できるのではないかと考えるのです。すると,定常過程における待ち行列長というのは離散型の確率変数となりますので,無記憶性を持つ離散型確率分布が幾何分布しかないことを踏まえると,定常過程における待ち行列長は幾何分布に従うことが予想されます。
ここで,到着のスピードがサービスのスピードよりも小さくなければ,行列長は無限大に発散してしまいます。したがって,平均到着率を$\lambda$,平均サービス率を$\mu$と置くと,$\lambda < \mu$となります。ただし,平均到着率と平均サービス率は以下を表します。
- 平均到着率:単位時間あたりの到着数
- 平均サービス率:単位時間あたりのサービス数
流入量よりも流出量の方が大きければ行列長は長くならないのではないかと思われる方もいらっしゃるかも知れません。しかし,$\lambda$と$\mu$というのは「平均」流入量と「平均」流出量です。常に$\lambda$流入して$\mu$流出するという訳ではなく,時間的に平均して考えると$\lambda$流入して$\mu$流出するということなのです。$\lambda$以上が流入する時間もありますし,$\mu$以下が流出する時間もあるため,行列長は長くなったり短くなったりします。
幾何分布のパラメータはコイントスが成功する確率,すなわち「全試行回数に対してどれだけの回数成功するか」を表しています。今回の例に当てはめると「単位時間あたりの流出量に対してどれだけの数が実質的に流出するか」を表すと考えられます。「実質的に流出する」量は,流出量から流入量を引いてあげることで求めることができます。具体的には,単位時間あたりに$\mu$だけ流出するという状況の中で,$\lambda$だけ新しく流入してきますから,実質的には$\mu-\lambda$だけ流出していることになります。したがって,行列長はパラメータ
\frac{\mu-\lambda}{\mu} &= 1-\rho
\end{align}
を持つ幾何分布に従うと考えられます。
流入量ではなく流出量を扱う理由は$\lambda < \mu$だからです。待ち行列が収束するためには平均流入量よりも平均流出量の方が大きくなければならないため,流出するという事象に着目するべきなのです。とはいえ,行列長が従う幾何分布のパラメータが「単位時間あたりの流出量に対してどれだけの数が実質的に流出するか」を表す$1-\rho$となる部分のロジックは曖昧です。ここは最速で結論に辿り着くための思考方法を説明するもので,数学的な正確性を担保するものではないことをご了承ください。
すると,幾何分布の平均より,定常過程における平均待ち行列長は式($\ref{平均待ち行列長}$)で表されることが分かります。さらに,指数分布の平均はパラメータの逆数であることから,一人当たりの平均待ち時間は$1/\mu$になります。平均待ち時間は,定常過程における平均待ち行列長に一人当たりの平均待ち時間$1/\mu$を掛ければよいため,式($\ref{平均待ち時間}$)で表されることも分かります。
定常分布のつりあいを利用
指数分布のパラメータは「単位時間あたりに事象が起こる回数」でしたので,平均到着率$\lambda$と平均サービス率$\mu$がそのまま指数分布のパラメータになることが分かります。
- 待ち行列の長さが$1$増加するのにかかる時間$t$は平均到着率$\lambda$をパラメータとする指数分布に従う
- 待ち行列の長さが$1$減少するのにかかる時間$t$は平均サービス率$\mu$をパラメータとする指数分布に従う
ここで,十分時間が経過した後の行列長の状態を定常状態と呼ぶことにします。状態というのは,単位時間ごとのある特定の行列長のことを指します。定常状態のインデックスを$n$と置き,その状態となる確率を$\pi_n$と置きます。まずは,インデックス$0$に着目しましょう。行列長は単位時間あたりに$\lambda$だけ増えるため,状態$1$は状態$0$から$\lambda$増えていることが分かります。逆に,状態$1$から状態$0$に時間を巻き戻すと,単位時間あたり$\mu$だけサービスを受けて戻ってきます。同様に,状態$n-1$,状態$n$,状態$n+1$の関係性を考えると,以下のように図示できます。
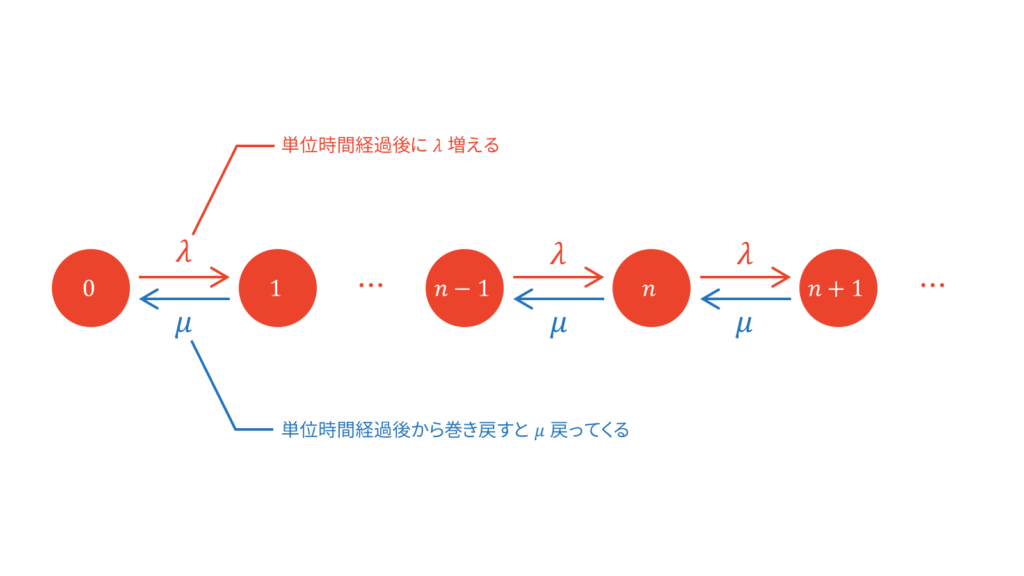
このように無記憶性を仮定する遷移を考えるモデルを連続時間マルコフ連鎖と呼びます。
上図より,状態$0$と状態$n$において行列から出ていく数の期待値は,
\begin{cases}
\lambda\pi_n & (n=0)\\[0.7em]
\lambda\pi_n + \mu\pi_n &(n>0)
\end{cases}
\end{align}
となります。一方で,状態$0$と状態$n$において行列に入ってくる数の期待値は,
\begin{cases}
\mu\pi_{n+1} & (n=0) \\[0.7em]
\lambda \pi_{n-1}+\mu\pi_{n+1}&(n>0)
\end{cases}
\end{align}
となります。定常状態においては,ある状態から他の状態に遷移する数の期待値と他の状態から遷移してくる数の期待値は等しくなければいけませんので,
\lambda\pi_{n}&=\mu\pi_{n+1}&(n=0) \\[0.7em]
(\lambda+\mu)\pi_n &=\lambda \pi_{n-1}+\mu\pi_{n+1}&(n>0)
\end{align}
が成り立ちます。改めて$\rho$を使って書き直しましょう。
\rho\pi_{n}&=\pi_{n+1}&(n=0)\label{つりあい1} \\[0.7em]
(1+\rho)\pi_n &=\rho \pi_{n-1}+\pi_{n+1}&(n>0) \label{つりあい2}
\end{align}
ここで,$\pi_n$は確率ですので,確率の定義より全てのインデックスに対しての総和は$1$になります。
\sum_{n=0}^{\infty} \pi_n &= 1 \label{定常状態の確率定義}
\end{align}
あとは,式($\ref{つりあい1}$),式($\ref{つりあい2}$),式($\ref{定常状態の確率定義}$)を連立させて$\pi_n$を求めるだけです。式($\ref{つりあい2}$)を変形すると,
\pi_{n+1}-\rho\pi_n &= \pi_{n}-\rho\pi_{n-1} \\[0.7em]
&= \ldots \\[0.7em]
&= \pi_{1}-\rho\pi_{0}
\end{align}
となります。さらに,式($\ref{つりあい1}$)より$\pi_{1} = \rho\pi_{0}$が得られます。したがって,
\pi_n &= \rho^{n}\pi_0 \label{pi_n}
\end{align}
が得られます。式($\ref{pi_n}$)を式($\ref{定常状態の確率定義}$)に代入すると,
\sum_{n=0}^{\infty} \rho^{n} \pi_{0} &= 1 \label{一般項}
\end{align}
が得られます。変形していきましょう。
\pi_{0} &= \left( \sum_{n=0}^{\infty} \rho^{n} \right)^{-1} \label{before}\\[0.7em]
&= \left( \frac{1}{1-\rho} \right)^{-1} \label{after}\\[0.7em]
&= 1-\rho \label{pi_0}
\end{align}
ただし,式($\ref{before}$)から式($\ref{after}$)は無限等比級数の公式を利用しました。式($\ref{pi_0}$)を式($\ref{一般項}$)に代入すると,
\pi_n &= (1-\rho)\rho^{n}
\end{align}
が得られます。これは,定常過程における待ち行列の長さを表す状態がパラメータを$1-\rho$とする幾何分布に従っていることを示しています。あとは,先ほどと同様に式($\ref{平均待ち行列長}$)と式($\ref{平均待ち時間}$)を求めることができます。
微分方程式を利用
時刻$t$で行列に$n$人並んでいる確率を$p_n(t)$と置きます。このとき,$p_n(t+\Delta t)$を$p_n(t)$を用いて漸化式で表し,導関数の定義を用いて微分方程式を出現させましょう。いま,時刻$t$において求める確率は以下の三つです。
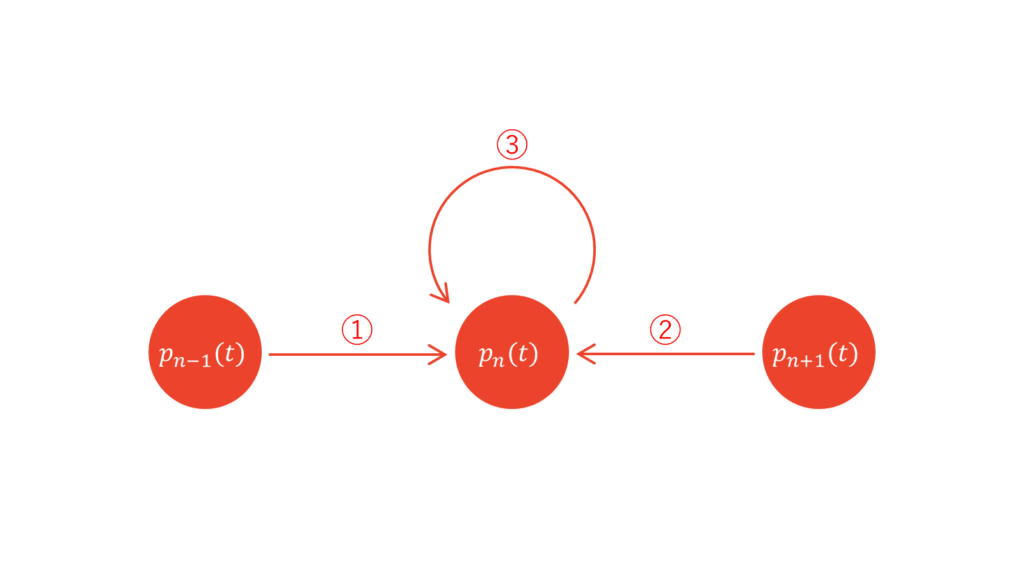
①は一人到着する遷移,②は一人抜ける遷移,③は到着もせず抜けもしない遷移のことを指します。なお,本来は$n-2$人からの遷移や$n+2$人からの遷移も考えるべきですが,$\Delta t$が微小量であることから$\Delta t$を二回以上掛ける遷移は無視していることに注意して下さい。
①と②に関しては,到着とサービスの時間間隔が指数分布に従うことを利用し,③は①と②の余事象を利用しましょう。①に関して,到着の時間間隔は指数分布に従います。指数分布のパラメータを$\lambda$と置くと,微小時間間隔$\Delta t$の間に新しい到着が$1$回発生する確率は
\int_{0}^{\Delta t} \lambda e^{-\lambda x}dx &= 1-e^{-\lambda \Delta t} \label{到着の微小時間間隔}
\end{align}
で表されます。なお,積分範囲が$[0,\Delta t]$となるのは指数分布の無記憶性に基づきます。式($\ref{到着の微小時間間隔}$)をマクローリン展開すると,
1-e^{-\lambda \Delta t} &= 1-\left\{ 1+\frac{(-\mu)}{1!}\Delta t+\frac{(-\mu)^2}{2!}(\Delta t)^2+\ldots \right\} \\[0.7em]
&= \lambda \Delta t + o\left(\Delta t\right)
\end{align}
となります。ただし,$o\left(\Delta t\right)$は$\Delta t$よりも高次の微小量を表します。二次の微小量を無視すると,①は$\lambda \Delta t$となります。サービスの時間間隔も指数分布に従うため,②は$\mu \Delta t$となります。③に関して,余事象より$1-\lambda \Delta t-\mu \Delta t$となります。以上の結果を図にまとめます。
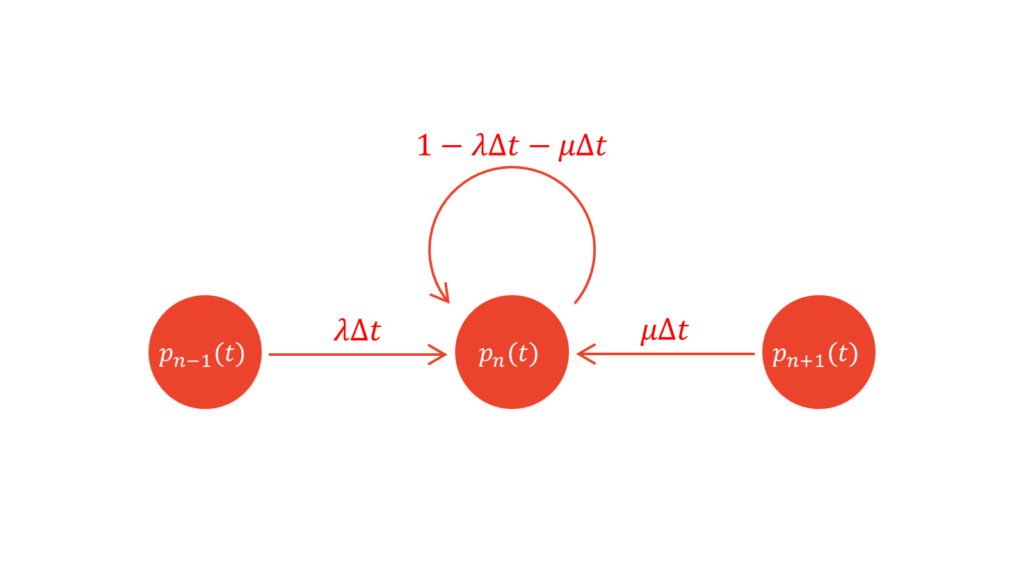
よって,$p_0(t+\Delta t)$と$p_n(t+\Delta t)$を漸化式で表すと,以下のようになります。
p_n(t+\Delta t) &= p_{n-1}(t)\lambda \Delta t + p_{n}(t)\left(1-\lambda \Delta t-\mu \Delta t\right)+p_{n+1}(t)\mu\Delta t \label{元の漸化式}
\end{align}
導関数の定義を持ち出すために変形します。
\frac{p_n(t+\Delta t)-p_{n}(t)}{\Delta t} &= p_{n-1}(t)\lambda - p_{n}(t)\left(\lambda+\mu \right)+p_{n+1}(t)\mu
\end{align}
両辺で$\Delta t \rightarrow 0$の極限を取ると,以下の微分方程式が得られます。
\frac{d}{dt}p_n(t) &= p_{n-1}(t)\lambda - p_{n}(t)\left(\lambda+\mu \right)+p_{n+1}(t)\mu
\end{align}
いま求めたいのは,十分時間が経過した後の定常分布であるため,確率$p_n(t)$が十分時間が経過した後に一定値に収束するとします。すなわち,$p_n(t)$の導関数は$0$になります。すると,微分方程式は以下のように三項間漸化式になります。
p_{n+1}(t) &= -p_{n-1}(t)\frac{\lambda}{\mu}+p_{n}(t)\left(1+\frac{\lambda}{\mu}\right) \\[0.7em]
&= -p_{n-1}(t)\rho+p_{n}(t)(1+\rho) \label{三項間漸化式}
\end{align}
ただし,$\rho=\lambda/\mu$と置きました。$\lambda < \mu$より$\rho < 1$であることに注意して下さい。これは,定常分布のつりあいの条件式($\ref{つりあい2}$)と等価になります。したがって,定常分布のつりあいのときと同様に,初期条件$p_{0}(t)$に関する微分方程式を求めましょう。これは,式($\ref{元の漸化式}$)と同様に求めることができます。ただし,$0$人の行列に対してはサービスを提供することができないため,$\mu \Delta t$が現れない点に注意して下さい。
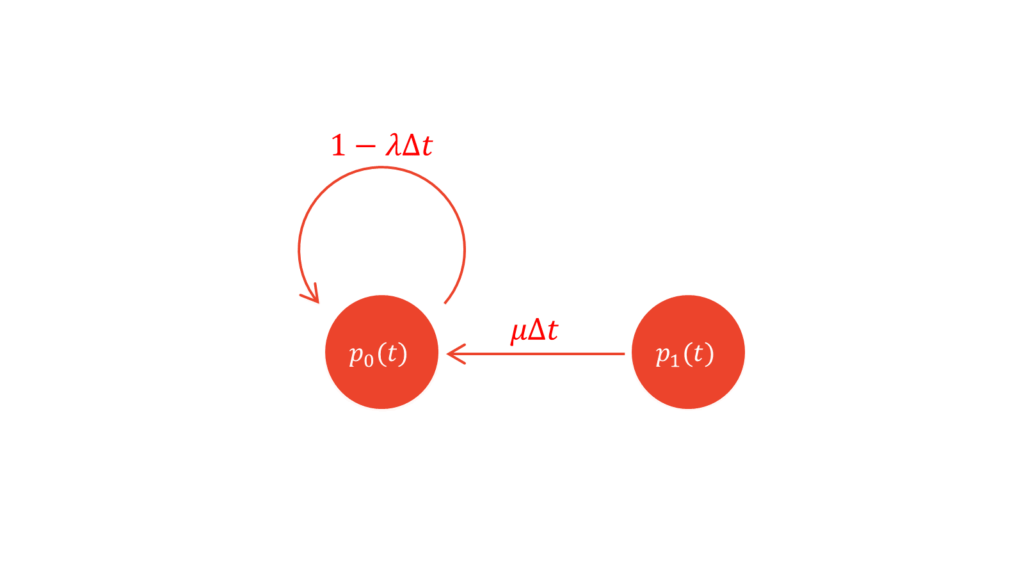
すなわち,$p_0(t)$に関する漸化式は以下のように表されます。
p_{0}(t+\Delta t) &= p_{0}(t)(1-\lambda \Delta t) + p_1(t)\mu \Delta t
\end{align}
先ほどと同様に微分方程式に変形し,定常分布の仮定$p^{\prime}_{0}(t)=0$を代入すると,
p_1(t) &= p_{0}(t)\rho \label{初期条件}
\end{align}
となります。これは,つりあいのときの条件式($\ref{つりあい1}$)と等価になります。あとは,定常分布のつりあいと同様に,確率の定義を利用して$p_{n}(t)$を求めるだけです。
参考文献
本稿の執筆にあたり参考にした文献は,以下でリストアップしております。


コメント