本記事は「これなら分かる!はじめての数理統計学」シリーズに含まれます。
不適切な内容があれば,記事下のコメント欄またはお問い合わせフォームよりご連絡下さい。
ポアソン分布
f_{X}(x) &= \frac{\lambda^x}{x!}e^{-\lambda} \\[0.7em]
G_{X}(s) &= e^{\lambda(s-1)} \\[0.7em]
E[X] &= \lambda \\[0.7em]
V[X] &= \lambda
\end{align}
二項分布$\Bin(n,p)$において,$np=\lambda>0$を一定に保ったまま$n$を大きくしていくとポアソン分布
\Po (\lambda)
\end{align}
が得られます。ポアソン分布に従う確率変数$X$に対し,実現値は
x &\in \{0, \ldots, n \}
\end{align}
であり,確率母関数の変数は$|s|\leq1$とします。ポアソン分布は再生性を持ち,ロードマップ中では二項分布の極限に相当します。
確率質量関数
ポアソン分布は,二項分布において$np=\lambda$を一定に保ちながら$n\rightarrow\infty$とすることで導かれます。$n$を大きくしていく中で$np$を一定に保つということは,$p$をその分小さくしていくことになります。要するに,ポアソン分布は稀にしか起こらない事象を表しているといえます。ここでは,ポアソン分布の確率質量関数を大まかに求める方法と,正確に計算する方法の両方をお伝えしていきます
二項分布のポアソン分布への収束は小数法則と呼ばれることもあります。
大まかに計算する方法
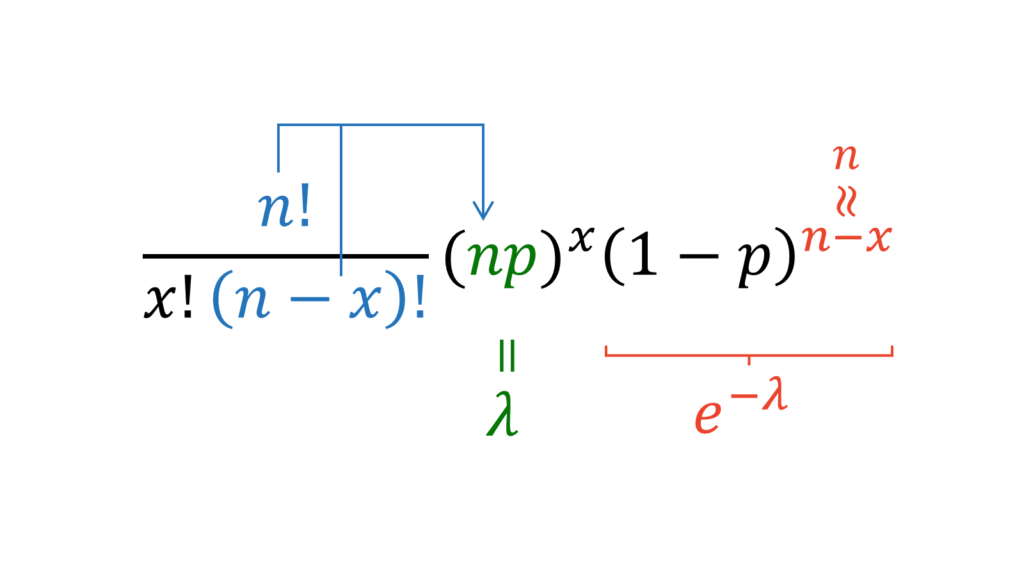
青色の部分は,分子の方が分母よりもおおよそ「$n$が$x$個分掛けられている分」だけ大きいことから,約分して$n^x$とみなします。$n^x$は$p^x$と同じ括弧の中に入れましょう。すると,緑色の部分は$np$の定義より$\lambda$となります。赤色の指数部分は,$n \rightarrow \infty$のときには$x$と比べて$n$の方が十分に大きいことから,$n-x$は$n$とみなすことができます。いま,$n=\lambda/p$ですので,ネイピア数の定義を利用すると,以下の変形により赤色の部分は$e^{-\lambda}$になります。
(1-p)^{n-x} &\approx (1-p)^{n} \\[0.7em]
&= \left\{ \left(1+\frac{1}{-n/\lambda} \right)^{-n/\lambda} \right\}^{-\lambda} \\[0.7em]
&\rightarrow e^{-\lambda}
\end{align}
すると,ポアソン分布の確率質量関数は以下のような形になると予想できます。
f_{X}(x) &= \frac{\lambda^x}{x!}e^{-\lambda}
\end{align}
正確に計算する方法
極限を正確に計算していきます。
f_{X}(x) &= P(X=x) \\[0.7em]
&= {}_n C _x p^x(1-p)^{n-x} \\[0.7em]
&= \frac{n!}{x!(n-x)!}\left(\frac{\lambda}{n}\right)^x \left( 1-\frac{\lambda}{n} \right)^{n-x}\\[0.7em]
&= \frac{n(n-1)\cdots(n-x+1)}{x!}\left( \frac{\lambda}{n} \right)^x\left(1-\frac{\lambda}{n} \right)^n \left(1-\frac{\lambda}{n} \right)^{-x}\\[0.7em]
&= \frac{\lambda^{x}}{x!}\left(1 - \frac{\lambda}{n} \right)^n
\left(1-\frac{1}{n} \right)\cdots \left(1-\frac{x-1}{n} \right)\left(1-\frac{\lambda}{n} \right)^{-x}\\[0.7em]
&= \frac{\lambda^{x}}{x!}\left\{\left(1 + \frac{1}{-n/\lambda}\right)^{-n/\lambda} \right\}^{-\lambda}
\left(1-\frac{1}{n} \right)\cdots \left(1-\frac{x-1}{n} \right)\left( 1-\frac{\lambda}{n} \right)^{-x}\\[0.7em]
&\longrightarrow \frac{\lambda^x}{x!}e^{-\lambda}\quad(n\rightarrow \infty)
\end{align}
確率母関数
確率母関数の定義に従って計算していきます。$e^{\lambda}$のマクローリン展開を利用します。
e^{s\lambda} &= 1 + \frac{s\lambda}{1!} + \frac{(s\lambda)^{2}}{2!} + \cdots
\end{align}
実際に計算していきましょう。
G_{X}(s) &= E[s^x]\\[0.7em]
&= \sum_{x=0}^{\infty} s^x e^{-\lambda}\frac{\lambda^x}{x!}\\[0.7em]
&= e^{-\lambda} \left\{ 1 + \frac{s\lambda}{1!} + \frac{(s\lambda)^{2}}{2!} + \cdots \right\}\\[0.7em]
&= e^{-\lambda} \cdot e^{s\lambda}\\[0.7em]
&= e^{\lambda(s-1)}
\end{align}
平均・分散
離散分布の平均と分散を求めるためには,確率母関数の性質を利用します。ポアソン分布は,期待値と分散が同じ値となります。まず,確率母関数の一階微分から$E[X]$を求めます。
E[X] &= \left.\frac{d G_{X}(s)}{d s}\right|_{s=1}\\[0.7em]
&= \left. \lambda e^{\lambda(s-1)} \right|_{s=1}\\[0.7em]
&= \lambda
\end{align}
次に,確率母関数の二階微分から$E[X(X−1)]$を求めます。
E[X(X-1)] &= \left.\frac{d^2 G_{X}(s)}{d s^2}\right|_{s=1}\\[0.7em]
&= \left. \lambda^2 e^{\lambda(s-1)} \right|_{s=1}\\[0.7em]
&= \lambda^2
\end{align}
最後に,分散の定義から分散を求めます。
V[X] &= E[X^2]-E[X]^2\\[0.7em]
&= E[X(X-1)] + E[X]-E[X]^2\\[0.7em]
&= \lambda^2 + \lambda-\lambda^2\\[0.7em]
&= \lambda
\end{align}
ポアソン分布の平均と分散は,上式のように「確率母関数を微分すると$\lambda$が前に出てきてそれ以外がキレイに消える」という感覚を覚えておくことで非常に素早く導出することができるようになります。
再生性
再生性を示すためには,再生性を示したい分布に従う独立な二つの確率変数を考え,その和の確率母関数を計算したときにパラメータが和の形になっていることを示します。いま,二つの独立な確率変数
X &\sim \Po (\lambda_x) \\[0.7em]
Y &\sim \Po (\lambda_y)
\end{align}
を考えます。 このとき,$X+Y$の確率母関数を計算します。
G_{X+Y}(s) &= G_{X}(s) \cdot G_{Y}(s) \\[0.7em]
&= e^{\lambda_x(s-1)} \cdot e^{\lambda_y(s-1)} \\[0.7em]
&= e^{(\lambda_x + \lambda_y)(s-1)}
\end{align}
これは,$X+Y$の確率母関数が$\Po (\lambda_x + \lambda_y)$の母関数であることを示しています。つまり,
X +Y &\sim \Po (\lambda_x + \lambda_y)
\end{align}
であり,ポアソン分布の再生性を示しています。
ロードマップ
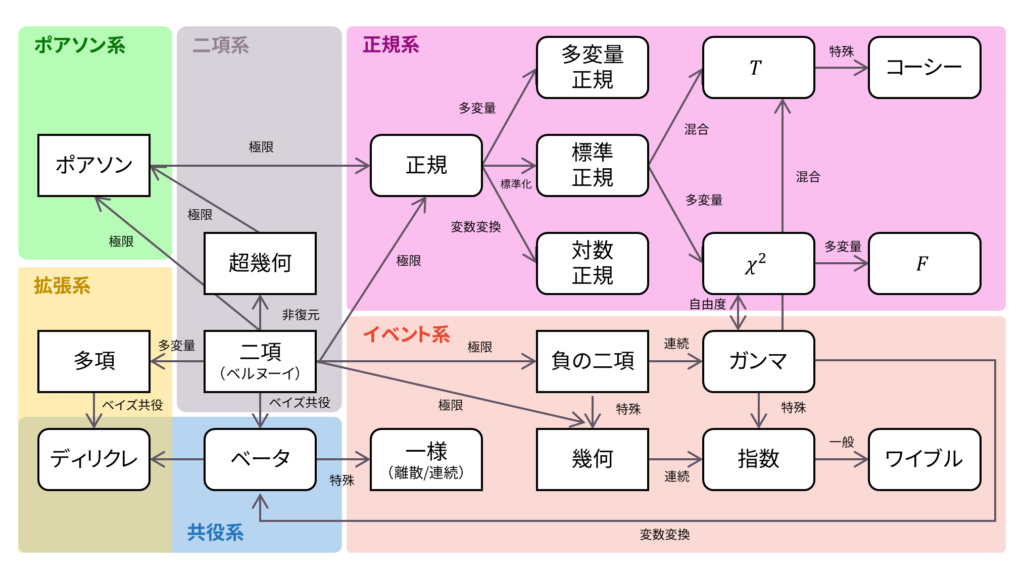
さて,ロードマップに戻ってみましょう。ポアソン分布は二項分布からの極限で表されました。以下の内容も参考になるでしょう。
参考文献
本稿の執筆にあたり参考にした文献は,以下でリストアップしております。


コメント
コメント一覧 (2件)
統計検定1級の勉強にいつも参考にしております。
細かいことで申し訳ないですが、式(12)は(1-p)^(1-x)ではなく(1-p)^(n-x)ではないでしぃうか?
riu様
ご指摘誠にありがとうございます。おっしゃる通りですので,本文を修正致しました。細かな指摘でも非常に助かりますmm