本記事は数学の徹底解説シリーズに含まれます。
初学者の分かりやすさを優先するため,多少正確でない表現が混在することがあります。もし致命的な間違いがあればご指摘いただけると助かります。
表現行列
$V,W$をそれぞれ$\mK$上の$n$次元,$m$次元ベクトル空間とし,$F:~V\rightarrow W$を$V$から$W$への線形写像とする。ただし,$\mK$は実数空間$\mR$または複素数空間$\mC$を表す。$\alpha=\{v_{1},\ldots,v_{n}\}$,$\beta=\{w_{1},\ldots,w_{m}\}$をそれぞれ$V,W$の基底とする。線形写像は行列により一意に定まることに注意して,$\mK^{n}$から$\mK^{m}$への線形写像$L_{A}$を定める$m\times n$行列を$A$とする。
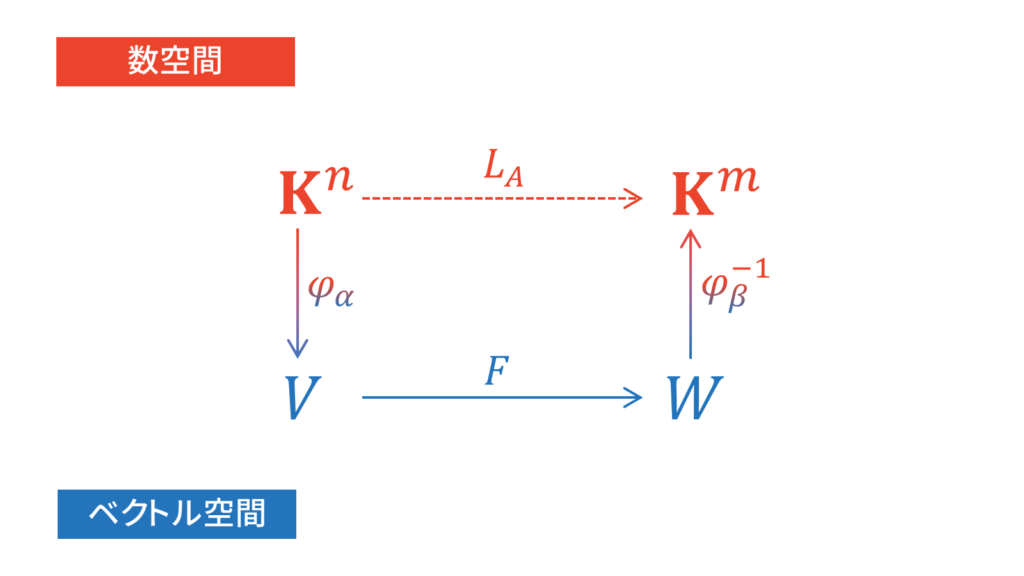
上図より,
\varphi_{\beta}^{-1}\circ F\circ \varphi_{\alpha} &= L_{A} \label{定義1}
\end{align}
となるような線形写像$L_{A}$を定める$m\times n$行列がただ一つ存在する。この行列$A$を$V$の基底$\alpha$,$W$の基底$\beta$に関する$F$の表現行列といい,
A &= [F]^{\alpha}_{\beta}
\end{align}
という記号で表す。
実数空間または複素数空間における線型変換をベクトル空間経由で考える点がポイントです。
補足
式($\ref{定義1}$)より,表現行列$A$は以下のように表すこともできます。
表現行列$A$の$(i,j)$要素を$a_{i,j}$と表すと,$a_{i,j}$は以下のように表される。
F(v_{j}) &= \sum_{i=1}^{m}a_{i,j}w_{i} \label{定義2}
\end{align}
すなわち,
\begin{cases}
F(v_{1}) &= a_{1,1}w_{1}+\cdots+a_{m,1}w_{m}\\[0.7em]
&\vdots \\[0.7em]
F(v_{n}) &= a_{1,n}w_{1}+\cdots+a_{m,n}w_{m}\label{完全形}
\end{cases}
\end{align}
が成り立つ。$A$は式($\ref{完全形}$)の係数並べた行列の転置として定義される。
式($\ref{完全形}$)の係数並べた行列がそのまま表現行列$A$となる訳ではなく,その転置として定義される点に十分注意してください。
式($\ref{定義2}$)を証明します。式($\ref{定義1}$)より,
F\circ \varphi_{\alpha} &= \varphi_{\beta}\circ L_{A} \label{大元}
\end{align}
が成り立ちます。$\mK^{n}$の標準基底を$\varepsilon=\{\ve_{1},\ldots,\ve_{n}\}$,$\mK^{m}$の標準基底を$\delta=\{\vd_{1},\ldots,\vd_{m}\}$とします。$\ve_{j}$の$F\circ \varphi_{\alpha}$による像は,
(F\circ \varphi_{\alpha})(\ve_{j}) &= F(\varphi_{\alpha}(\ve_{j})) \\[0.7em]
&= F(v_{j}) \label{布石1}
\end{align}
と表されます。一方,$\ve_{j}$の$\varphi_{\beta}\circ L_{A}$による像は,線形写像と行列の関係を利用すると,
(\varphi_{\beta}\circ L_{A})(\ve_{j}) &= \varphi_{\beta}(L_{A}(\ve_{j})) \\[0.7em]
&= \varphi_{\beta}(\va_{j}) \label{代入対象}
\end{align}
と表されます。いま,$\va_{j}$は行列$A$の列ベクトルであり,行列$A$の行方向は$\mK^{m}$の次元に相当することに注意します。
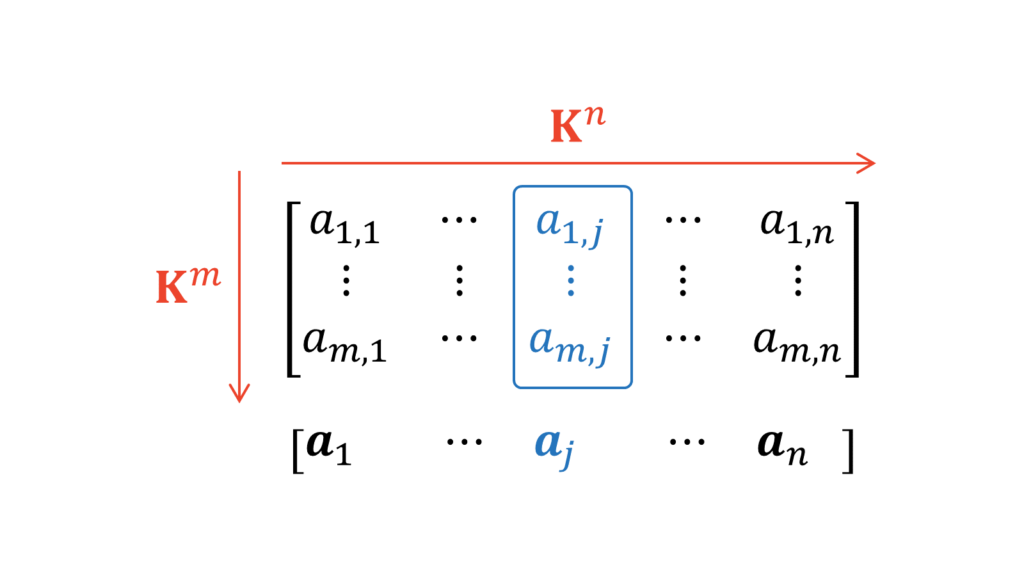
すなわち,以下のように$\mK^{m}$の標準基底の一次結合で表すことができます。
\va_{j} &= \sum_{i=1}^{m}a_{ij}\vd_{i} \label{一次結合}
\end{align}
式($\ref{一次結合}$)を式($\ref{代入対象}$)に代入すると,
(\varphi_{\beta}\circ L_{A})(\ve_{j})
&= \varphi_{\beta}\left(\sum_{i=1}^{m}a_{ij}\vd_{i}\right) \\[0.7em]
&= \sum_{i=1}^{m}a_{ij}\varphi_{\beta}(\vd_{i}) \\[0.7em]
&= \sum_{i=1}^{m}a_{ij}w_{i}\label{布石2}
\end{align}
が得られます。式($\ref{布石1}$)と式($\ref{布石2}$)を式($\ref{大元}$)に代入すると,式($\ref{定義2}$)が得られます。


コメント