統計検定1級の過去問解答解説を行います。目次は以下をご覧ください。
不適切な内容があれば,記事下のコメント欄またはお問い合わせフォームよりご連絡下さい。
問題
統計検定1級の過去問からの出題になります。統計検定の問題の著作権は日本統計学会に帰属していますので,本稿にて記載することはできません。「演習問題を俯瞰する」で詳しく紹介している公式の過去問題集をご購入いただきますようお願い致します。
解答
連続一様分布と条件付き確率分布に関する出題でした。連続一様分布の確率密度関数は面積の逆数で与えられることに気付くことができれば,解答は易しかったでしょう。
(1)
$-1\leq U,V \leq 1$に対し,$U$と$V$の累積分布関数は
F_{1}(u) &= \frac{u+1}{2},\quad
F_{2}(v) = \frac{v+1}{2}
\end{align}
となる。$U,V$はそれぞれ$[-1,1]$上の一様分布に従う。
与えられた同時累積分布関数を$v$に関して周辺化することにより,
F_{1}(u) &= \int_{-1}^{1}\frac{uv+u+v+1}{4}dv
= \frac{u+1}{4}+\frac{u+1}{4}\left[\frac{v^{2}}{2}\right]_{-1}^{1}
= \frac{u+1}{2}\label{1-1}
\end{align}
と求められます。また,与えられた同時累積分布関数は$u,v$に関して対称であることから,$F_{2}(v)$は$F_{1}(v)$と等しくなるため,$F_{2}(v)=(v+1)/2$となります。$u,v$の確率密度関数をそれぞれ$f_{1},f_{2}$とおくと,確率密度関数は累積分布関数の微分により得られることから,
f_{1}(u) &= \frac{d}{d u}F_{1}(u) = \frac{1}{2},\quad
f_{2}(v) = \frac{d}{d v}F_{2}(v) = \frac{1}{2}\label{f}
\end{align}
と求められます。したがって,$U,V$ともに$[-1,1]$上の一様分布に従うことが分かりました。
$F_{1}(u)$と$F_{2}(u)$が求められた時点で,一様分布の累積分布関数の形となっていることが分かります。ただし,一様分布の累積分布関数を導出せずに用いるよりは,上記解答のように確率密度関数まで求めてしまった方が安全です。
(2)
$U$と$V$は独立であり,$[-1,1]\times[-1,1]$上の一様分布に従う。
f(u,v) &= \frac{\partial^{2}F(u,v)}{\partial u\partial v}
= \frac{1}{4}\frac{\partial^{2}}{\partial u\partial v}(uv+u+v+1)
= \frac{1}{4}
\end{align}
となります。式($\ref{f}$)より,
f(u,v) &= \frac{1}{4} = f_1(u)\cdot f_{2}(v)
\end{align}
が成り立ちますので,独立の定義より$U$と$V$は独立になります。また,同時確率密度関数が一定値であることから,$(U,V)$は$[-1,1]\times[-1,1]$上の一様分布に従います。
(3)
P(U^{2}+V^{2}\leq 1) &= \frac{\pi}{4}
\end{align}
$-1\leq U,V \leq 1$に対し,$U^{2}+V^{2}\leq 1$は半径$1$の円の面積を表します。$(U,V)$が$[-1,1]\times[-1,1]$上を一様に動くとき,$(U,V)$が$U^{2}+V^{2}\leq 1$の内部にある確率は面積比を考えればよく,
P(U^{2}+V^{2}\leq 1) &= \frac{\pi}{4}
\end{align}
と求められます。
補足
後の問題のため,補足として変数変換による解法を紹介します。以下の極座標変換を考えます。
U &= R\cos\Theta,\quad
V = R\sin\Theta
\end{align}
ただし,$-1\leq U,V\leq 1$のとき,$0\leq R\leq 1$,$0\leq \Theta\leq 2\pi$となることに注意してください。
極座標変換は独立性を失わないため,$(U,V)$が独立のときは$(R,\Theta)$も独立になります。
ヤコビアンは
J(r, \theta)
&{=} \left|
\begin{array}{cc}
\partial (r\cos)\theta/ \partial r & \partial (r\cos)\theta / \partial \theta \\[0.7em]
\partial (r\sin)\theta/ \partial r & \partial (r\sin)\theta / \partial \theta
\end{array}
\right|
{=} \left|
\begin{array}{cc}
\cos\theta & -r\sin\theta \\[0.7em]
\sin\theta & r\cos\theta
\end{array}
\right|
{=} r(\cos^{2}\theta+\sin^{2}\theta)
{=} r
\end{align}
となるため,$(R,\Theta)$の同時確率密度関数を$g$とおくと,確率変数の変数変換の性質より,
g(r,\theta) &= f(r,\theta)\cdot |J(r,\theta)| = \frac{r}{4}
\end{align}
となります。したがって,
P(U^{2}+V^{2}\leq 1) = P(R^{2}\leq 1)
= \int_{0}^{2\pi}\int_{0}^{1}\frac{r}{4}drd\theta
= \frac{\pi}{4}
\end{align}
となります。
(4)
P(U^{2}{-}2UV{+}V^{2}{\leq}1) &= \frac{3}{4}
\end{align}
この問題では,$X{=}U{-}V$とおいて変数変換を考えたくなりますが,結局$(U,V)$のまま考えていく場合と同様の手続きが必要になります。さらに,次の問題で$(U,V)$の相関係数を求めさせており,ここで変数変換を用いると次の問題で逆変換を考えなければならず,二度手間となってしまいます。そこで,与えられた$(U,V)$をそのまま考えていきます。いま,
P(U^{2}{-}2UV{+}V^{2}{\leq}1)
&{=} P((U{-}V)^{2}{\leq}1)
{=} P(-1{\leq}U{-}V{\leq}1)
{=} P(-1{+}V{\leq}U{\leq}1{+}V)
\end{align}
に注意すると,前問と同様に$(U,V)$の定義域の面積と$-1{\leq}U,V{\leq}1$かつ$-1{+}V{\leq}U{\leq}1{+}V$の囲む面積の比を考えればよいことが分かります。前問の通り前者は$4$であり,後者を図示して面積を求めると$3$となるため,求める確率は$3/4$となります。
別解
$-1{\leq}U,V{\leq}1$かつ$-1{+}V{\leq}U{\leq}1{+}V$を数直線で考えると,
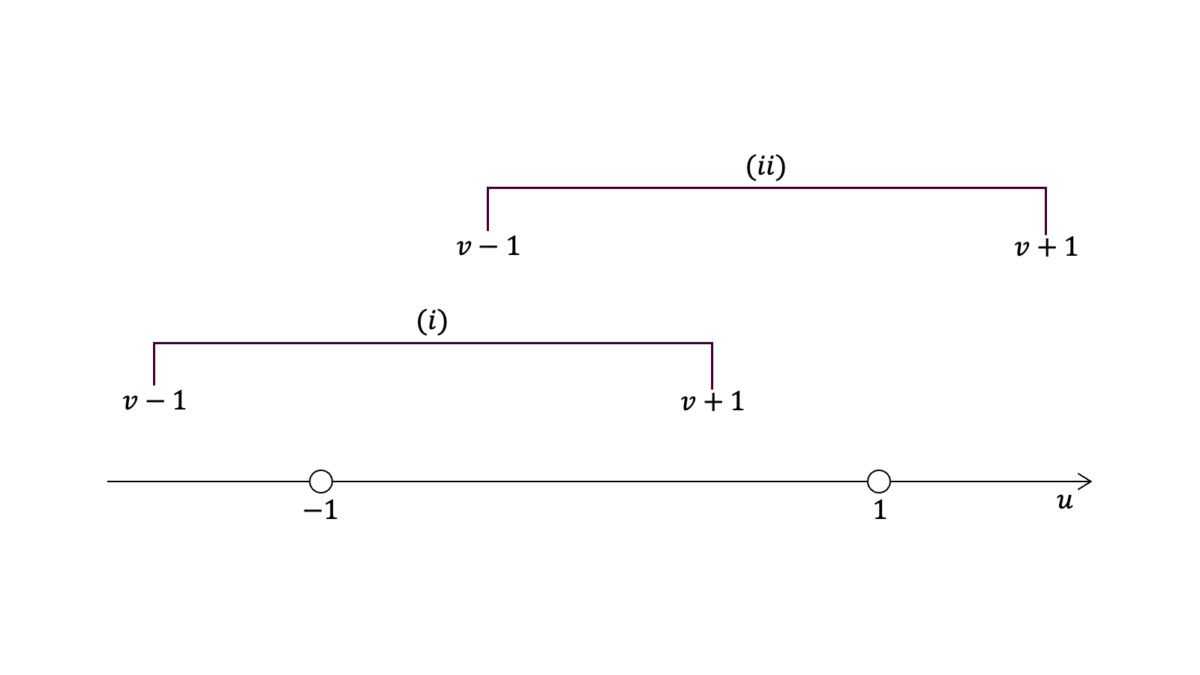
のように$-1<v<0$と$0<v<1$で場合分けすればよいことが分かります。したがって,
P(-1{+}V{\leq}U{\leq}1{+}V)
&= \int_{-1}^{0}\int_{-1}^{v+1}\frac{1}{4}dudv+\int_{0}^{1}\int_{v-1}^{1}\frac{1}{4}dudv\\[0.7em]
&= \int_{-1}^{0}\frac{2+v}{4}dv+\int_{0}^{1}\frac{2-v}{4}du
= \frac{3}{8}+\frac{3}{8} = \frac{3}{4}
\end{align}
となります。
(5)
\rho &= \frac{1}{2}
\end{align}
条件$u^{2}{-}2uv{+}v^{2}{\leq}1$を$d$とおきます。一様分布の確率密度関数は定義域によって囲まれる面積の逆数として定義されることに注意すると,前問より条件$f(u,v|d){=}1/3$となります。前問と同様にして$v$の周辺確率密度関数は
f(v) &=
\begin{cases}
\displaystyle
\int_{-1}^{v+1}\frac{1}{3}du = \frac{2+v}{3}&\quad(-1<v<0)\\[0.7em]
\displaystyle
\int_{v-1}^{1}\frac{1}{3}du = \frac{2-v}{3}&\quad(0<v<1)
\end{cases}
\end{align}
となります。
$f(v)$と書いていますが,厳密には$d$により条件付けられた確率密度関数の周辺確率密度関数です。
$f(v)$は$v{=}0$を軸として対称であることから,$E[V]{=}0$となります。さらに,分散は
V[V] &= E[V^{2}] - E[V]^{2} = E[V^{2}] = \int_{-1}^{0}v^{2}\frac{2+v}{3}dv+\int_{0}^{1}v^{2}\frac{2-v}{3}dv = \frac{5}{18}
\end{align}
となります。一方,共分散は
\Cov[U,V]
&= E[UV]-E[U]E[V]\\[0.7em]
&= E[UV]\\[0.7em]
&= \int_{-1}^{0}\int_{-1}^{v+1}uv\frac{1}{3}dudv+\int_{0}^{1}\int_{v-1}^{1}uv\frac{1}{3}dudv\\[0.7em]
&= \frac{1}{6}\int_{-1}^{0}(v^{3}+2v^{2})dv+\frac{1}{6}\int_{0}^{1}(-v^{3}+2v^{2})dv\\[0.7em]
&= \frac{5}{72}+\frac{5}{72} = \frac{5}{36}
\end{align}
となります。したがって,相関係数は
\rho &= \frac{\Cov[U,V]}{\sqrt{V[U]}\sqrt{V[V]}} = \frac{5/36}{5/18} = \frac{1}{2}
\end{align}
となります。


コメント
コメント一覧 (2件)
式(17)2式目 積分範囲は[v-1,1]の誤植ですか?
yakata66 さま
ご指摘ありがとうございます。反応が遅くなり大変恐縮ですが,本文を修正しました。