統計検定1級の過去問解答解説を行います。目次は以下をご覧ください。
不適切な内容があれば,記事下のコメント欄またはお問い合わせフォームよりご連絡下さい。
問題
統計検定1級の過去問からの出題になります。統計検定の問題の著作権は日本統計学会に帰属していますので,本稿にて記載することはできません。「演習問題を俯瞰する」で詳しく紹介している公式の過去問題集をご購入いただきますようお願い致します。
解答
二つの連続型確率変数の確率密度関数と独立性に関する問題です。
(1)
期待値の定義にしたがって計算します。まずは,$X$の期待値を求めます。
E[X]
&= \int_{0}^{\infty}xe^{-x}dx
= \left[x(-e^{-x})\right]_{0}^{\infty} + \int_{0}^{\infty}e^{-x}dx
= 1
\end{align}
部分積分を使わなくても,ガンマ関数を利用して$\Gamma(2)=1$と求めることもできます。
同様に,$Y$の期待値を求めます。
E[Y]
&= \int_{0}^{1}y~dy
= \frac{1}{2}
\end{align}
(2)
確率変数と独立の性質より,$XY$の期待値は以下のように求められます。
E[XY] &= E[X]E[Y] s= \frac{1}{2}
\end{align}
(3)
$X,Y$が独立のとき,確率変数の和の分布と畳み込みより,$Z=X+Y$の確率密度関数は$W=Y$を用いて
f_{Z}(z) &= \int_{-\infty}^{\infty}f_{X}(z-w)f_{Y}(w)dw\\[0.7em]
&=\int_{0}^{1}f_{X}(z-w)dw
\end{align}
と表されます。ここで,$z$を固定して$w$を変数とみると,
f_{X}(z-w) &=
\begin{cases}
e^{w-z} & (w<z)\\[0.7em]
0 & (z\leq w)
\end{cases}
\end{align}
と場合分けできます。$w$が積分範囲$[0,1]$を動くことを考えると,$z\leq0$の場合,$0<z<1$の場合,$1\leq z$の場合の三通りを考えればよいです。まず,$z\leq0$の場合を考えます。常に$z\leq w$となりますので,
f_{Z}(z) &= \int_{0}^{1}0~dw = 0
\end{align}
となります。次に,$0<z<1$の場合を考えます。$w<z$のときのみ$f_{X}(z-w)=e^{w-z}$となりますので,
f_{Z}(z) &= \int_{0}^{z}e^{-z+w}dw = \left[e^{-z+w}\right]_{0}^{z} = 1-e^{-z}
\end{align}
となります。最後に,$1\leq z$の場合を考えます。$w$の積分区間$[0,1]$で常に$f_{X}(z-w)=e^{w-z}$となりますので,
f_{Z}(z) &= \int_{0}^{1}e^{-z+w}dw = \left[e^{-z+w}\right]_{0}^{1} = e^{-z}(e-1)
\end{align}
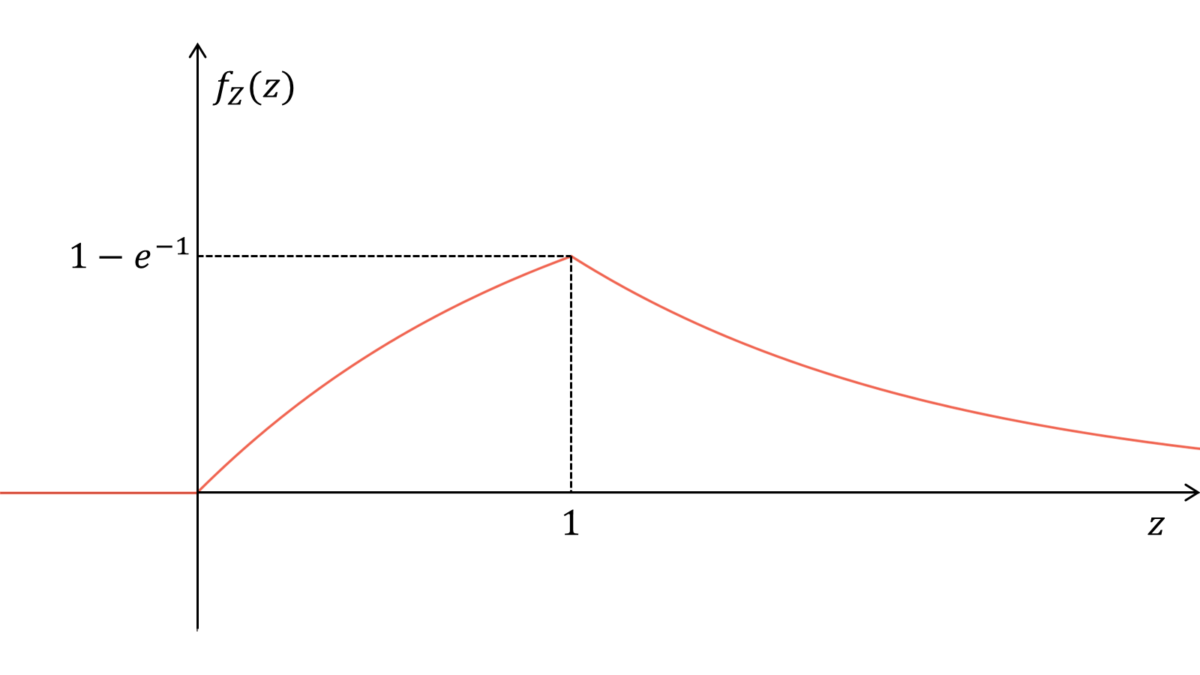
となります。以上より,$f_{Z}(z)$は以下のように表されます。
f_{Z}(z) &=
\begin{cases}
0 & (z\leq0)\\[0.7em]
1-e^{-z} & (0<z<1)\\[0.7em]
e^{-z}(e-1) & (1\leq z)
\end{cases}
\end{align}
グラフは以下のようになります。
(4)
$h(x)$の単調性,すなわち$X$から$Y$への変換前後で順序が保存されることに着目します。確率変数$X$がある実現値$x$以下の値をとるとき,
P(X\leq x) &= P(h(X)\leq h(x))\label{順序}
\end{align}
が成り立ちます。$P(X\leq x)$は累積分布関数そのものですので,式($\ref{順序}$)は
F_{X}(x) &= F_{Y}(y)\label{累積分布関数_順序}
\end{align}
と表されます。$f_{X}(x)$は与えられていますから,累積分布関数の定義から$F_{X}(x)$を計算しましょう。
F_{X}(x) &= \int_{0}^{x}e^{-u}du = 1-e^{-x}\label{累積分布関数_x}
\end{align}
同様に,$f_{Y}(y)$から$F_{Y}(y)$を計算しましょう。
F_{Y}(y) &= \int_{0}^{y}1~dv = y\label{累積分布関数_y}
\end{align}
$y=h(x)$に注意して,式($\ref{累積分布関数_x}$)と式($\ref{累積分布関数_y}$)を式($\ref{累積分布関数_順序}$)に代入すると,
1-e^{-x} &= y = h(x)
\end{align}
が得られます。次に,$XY$の期待値を求めます。確率変数の性質より,
E[XY] &= E[Xh(X)] = E[X(1-e^{-X})] = E[X]-E[Xe^{-X}] = 1- E[Xe^{-X}]
\end{align}
が成り立ちます。ただし,$E[\cdot]$は$f_{X}$に対する期待値であることに注意してください。すると,
E[Xe^{-X}] &= \int_{0}^{\infty}xe^{-x}\cdot e^{-x}dx\label{ガンマ関数前}\\[0.7em]
&= \left[x\left(-\frac{e^{-2x}}{2}\right)\right]_{0}^{\infty}+\frac{1}{2}\int_{0}^{\infty}e^{-2x}dx\\[0.7em]
&= 0+\frac{1}{2} \left[\left(-\frac{e^{-2x}}{2}\right)\right]_{0}^{\infty}
= \frac{1}{4}
\end{align}
と計算できます。
部分積分を使わなくても,式($\ref{ガンマ関数前}$)をガンマ関数が出現するように形に変形し,$\Gamma(2)=1$を利用して求めることもできます。
以上より,
E[XY] &= 1- E[Xe^{-X}] = 1 - \frac{1}{4} = \frac{3}{4}
\end{align}
が得られます。
別解
一次元の場合の確率変数の変数変換を利用しても解くことができます。$f_{Y}(y)$を$Y{=}h(X)$により$f_{X}(x)$に変換することを考えます。一次元のヤコビアンは変換に利用する関数の導関数であること,$h$の単調性より$h^{\prime}(x)\geq 0$となることに注意すると,
f_{X}(x) &= f_{Y}(h(x))\left|J(x)\right| = f_{Y}(h(x))h^{\prime}(x)\label{一次元の変数変換}
\end{align}
が成り立ちます。
ヤコビアンが変換前後の面積比を保存するための調整であることを思い出してください。
$x>0$かつ$0<y= h(x)<1$のとき,式($\ref{一次元の変数変換}$)に$f_{X}(x)$と$f_{Y}(y)$を代入すると,
e^{-x} &= h^{\prime}(x)
\end{align}
が得られます。両辺を$x$で積分すると,
h(x) &= -e^{-x} + C\label{Cあり}
\end{align}
が得られます。ここで,$C$を求めるため$f_{X}$が定義される$0{<}x$を考えます。$h$が単調増加関数かつ$0{<}h(x){<}1$であることに注意すると,$h(0)=0$かつ$h(x)の$右側極限は$1$となり,$C{=}1$が得られます。
仮に$h(0)=0$かつ$h(x)$の右側極限は$1$でないと仮定すると,$y$の定義域が$(0,1)$ではなくなるため不適切です。例えば,$h(x)$の右側極限が$1/2$である場合,$f_{Y}(y)$は$(0,1/2)$の区間で$1$となり,定義域で積分しても$1$とならず確率密度関数の定義を満たさなくなってしまいます。$[1/2,1)$の区間の$y$が定義されず,与えられた$f_{Y}(y)$を満たさない,と解釈してもよいでしょう。
したがって,$h(x)=1-e^{-x}$が得られます。同様にして,$E[XY]$を求められます。


コメント
コメント一覧 (2件)
統計検定1級の過去問の勉強をしておりこのページにたどり着きました。
とても丁寧で分かりやすい解説で助かっております。
この問題に関して1点わからない点があるので質問させてください。
(4)の別解にて「h(x)が単調増加関数かつ0<h(x)<1であることに注意すると,h(x)の右側極限は1となります」との記載があります。
単調増加性と有界性からh(x)の右側極限は1以下になることは分かりますが、1となるのはどうしてでしょうか?
よろしければお教え頂ければ幸いです。
nagatani様
ご質問ありがとうございます。私の理解を本文に追記しました。間違いがある場合はご指摘いただけないでしょうか。よろしくお願い致します。