北川 博之著「データベースシステム(オーム社)」を参考に,データベースシステムの知識をまとめます。
結論
データベースの正規化は,データ挿入・更新・削除時の不整合を防止するために行われる分解操作のことを指す。課される制約の種類により,正規化は以下のように分類される。
- 第一正規形:セルの結合がない
- 第二正規形:属性間の依存関係に弱い制約を課している(部分関数従属性の排除)
- 第三正規形:属性間の依存関係にやや強い制約を課している(推移的関数従属性の排除)
- ボイス・コッド正規形:属性間の依存関係に強い制約を課している
- 第四正規形:タスキ掛けのような明らかな冗長性がない
- 第五正規形:複数の表の結合として分解不可能な最小単位である
はじめに
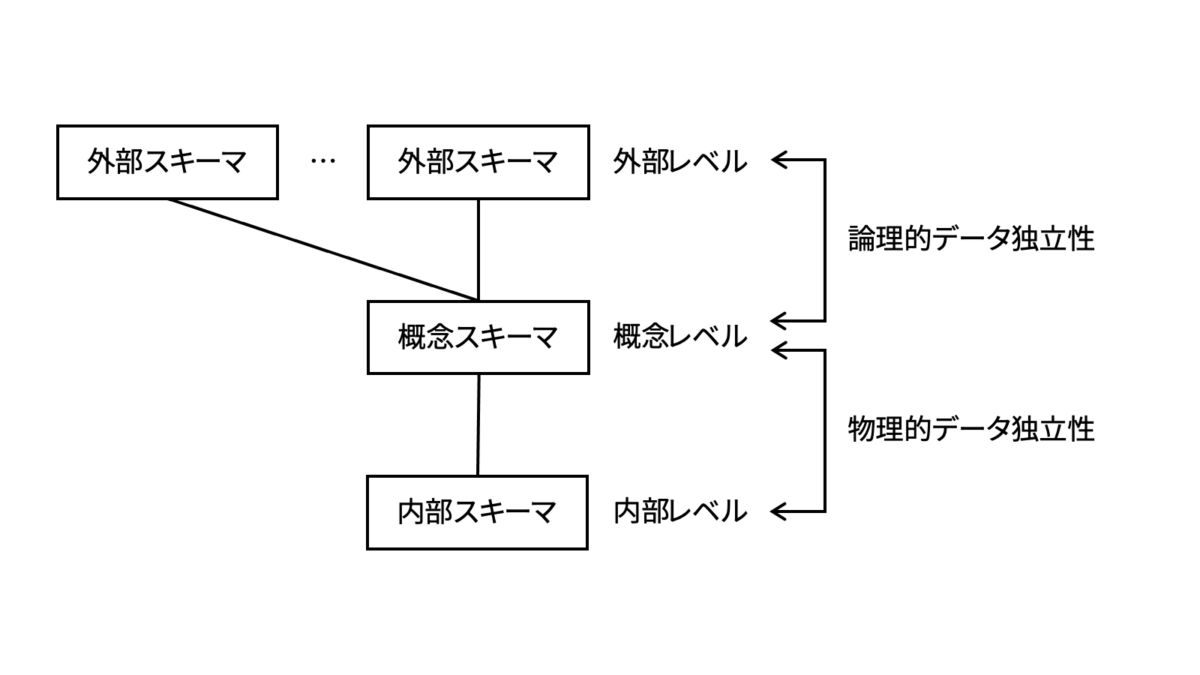
今日のデータベースシステムは,複数の応用目的での共有を意図して組織的かつ永続的にデータ群を格納するために利用されています。データベース中のデータの構造,形式,関連,各種整合性制約等を記述したものをスキーマと呼び,「外部スキーマ」「概念スキーマ」「内部スキーマ」と三階層に分ける解釈方法が一般的です。
内部スキーマとは,物理的なデータの管理方法を規定したルールのことを指します。概念スキーマとは,データベース全体を論理的に記述したルールのことを指します。外部スキーマとは,アプリケーションに対するデータの提供方法を規定したルールのことを指します。これらのスキーマ間には,従来のファイルシステムにおける問題点を克服するために,論理的・物理的なデータ独立性をもたせます。
実世界のデータは複雑で難解であるため,データベースシステムに落とし込むにはデータベース設計を行う必要があります。古くから研究が盛んなデータベース設計には,「概念設計」と「論理設計」があります。
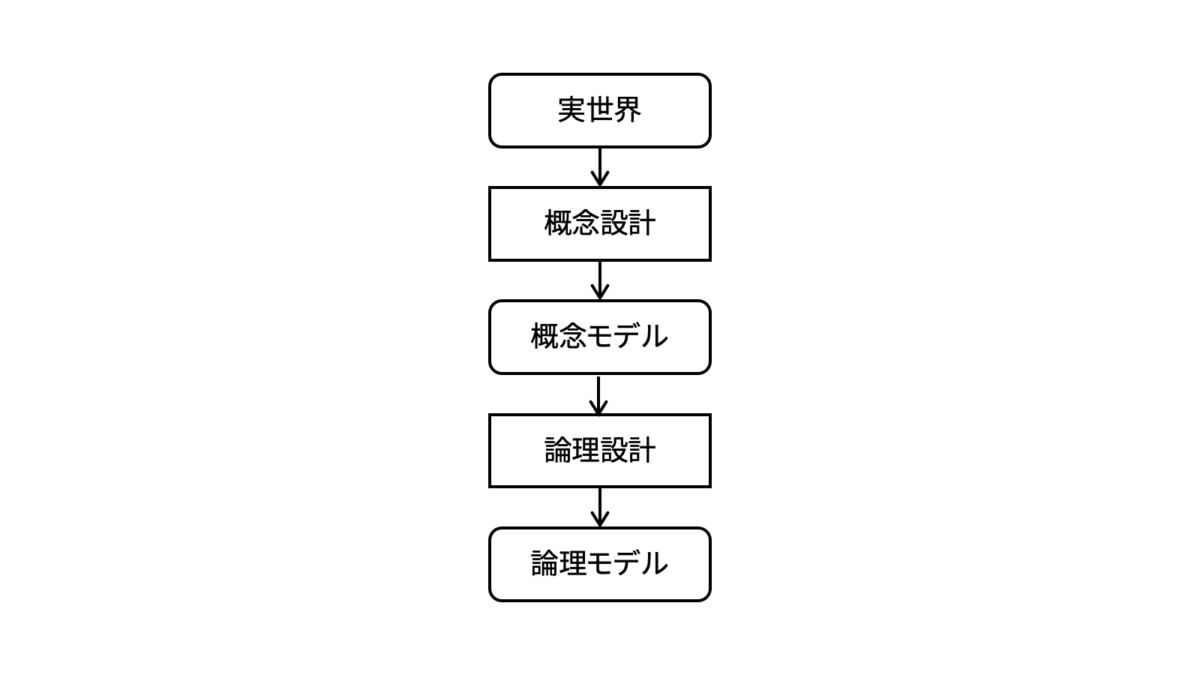
概念設計では,実世界をDBMSでどのように構造化するかを規定します。実体関連モデルを作成すると捉えておけばよいでしょう。論理設計では,DBMSが提供するデータモデルを作成します。概念スキーマを作成すると捉えておけばよいでしょう。データベース設計の目的は,概念スキーマの作成であることをおさえてください。
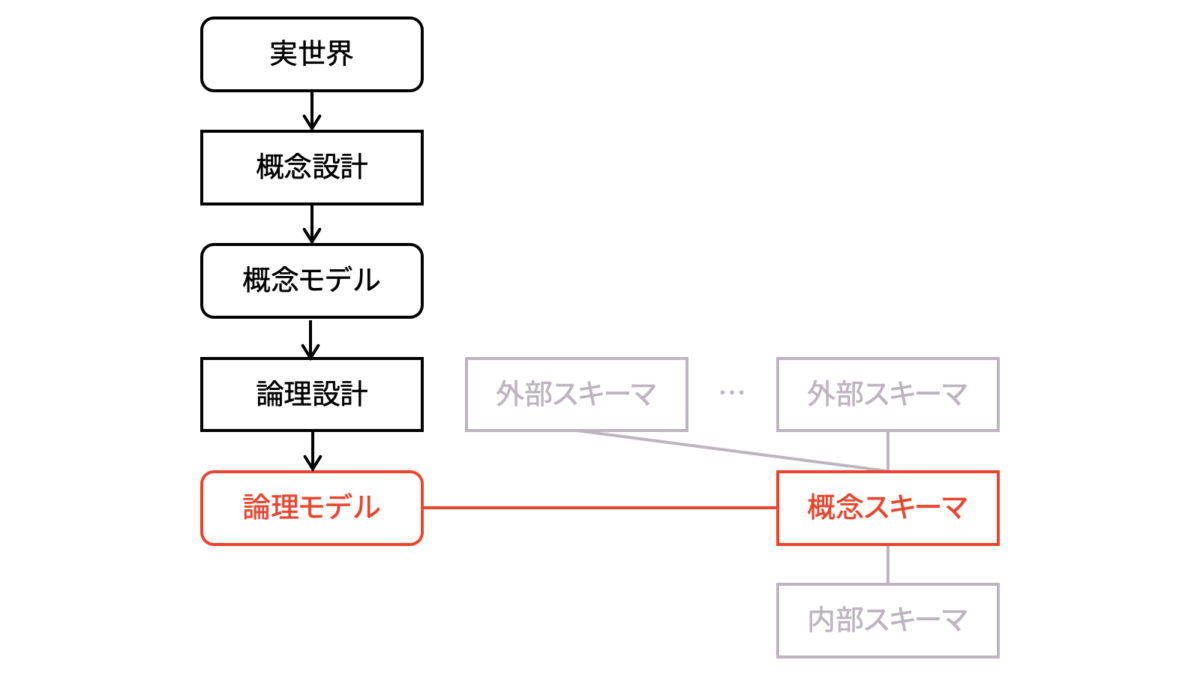
格納するデータ構造のルールと整合性制約を定めるデータモデルとしては,リレーショナルデータモデルがデファクトスタンダードとなっています。したがって,以下では「データベース」という曖昧な用語を,リレーションスキーマ,およびリレーションスキーマの集合と関連する整合性制約の集合として定義されるリレーショナルデータベーススキーマという用語により表現します。
正規化とは
前述の通り,概念設計では実体関連モデルを利用することで概念モデルを作成することが可能です。論理設計では,Teoryらによって提案された手法により,実体関連モデルからリレーショナルデータベーススキーマを導出することができます。
しかしながら,この手法だけで導出されたリレーショナルデータベーススキーマでは,更新不整合を引き起こしてしまう可能性があります。そこで,データベース設計の歴史では,論理設計の中でデータベースの正規化を行うことにより更新不整合を極力防ごうとしてきました。すなわち,データベースの正規化とは,更新不整合を防ぐために元のリレーションスキーマの情報をなるべく保ちながらリレーションスキーマを変形する操作のことを指します。
「データベースの正規化」という用語がよく使われていますが,正確に表現するならば「リレーションスキーマの正規化」となります。本稿のタイトルは,検索エンジン経由での流入を考慮して「データベースの正規化」としています。
正規化の種類
更新不整合を防ぐためにリレーションスキーマの各種制約を課すことで,リレーションスキーマを正規化します。これらの制約に応じて,正規形には第一正規形〜第五正規形とボイス・コッド正規形の計六種類があります。ボイス・コッド正規形は,第三正規形と第四正規形の中間的な正規形のことを指します。数字の大きな正規形は数字の小さな正規形の制約を徐々に強めていくため,数字の大きなは正規形は小さな正規形を内包します。
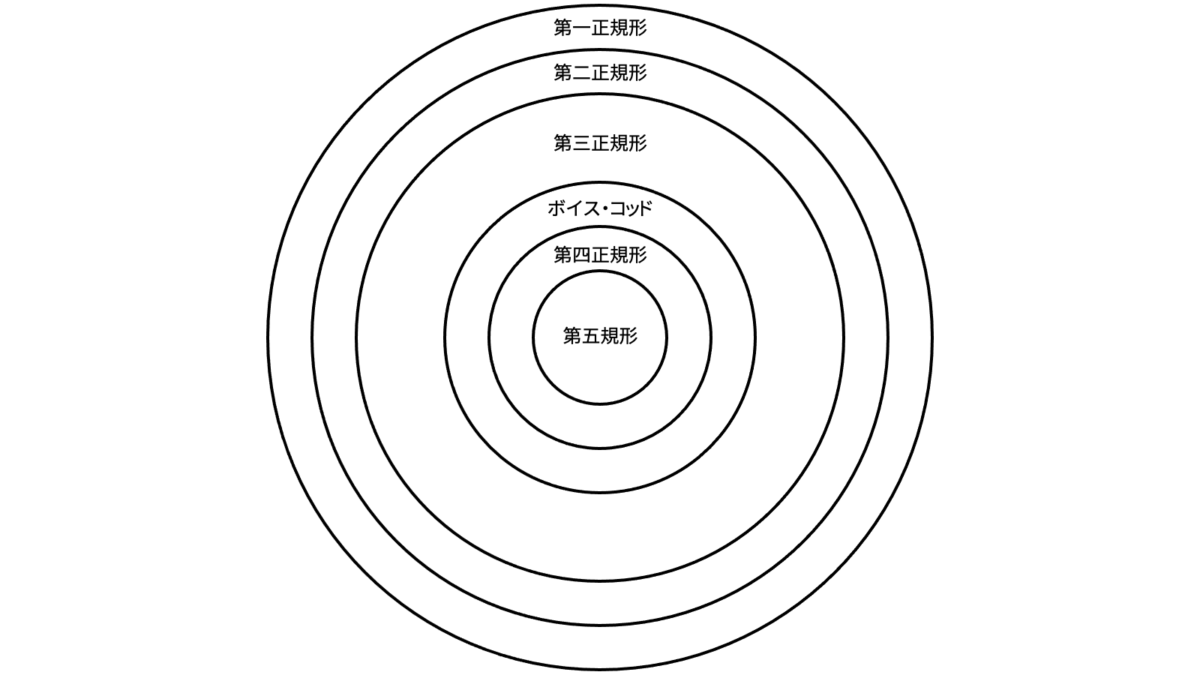
それぞれの正規形は,リレーションに課される制約の種類が異なります。前述の通り,数字が大きくなるほどリレーションスキーマに強い制約を課していくため,更新不整合を引き起こす可能性が低くなっていきます。しかし,第三正規形からボイス・コッド正規形への分解は,従属性保存を犠牲にします。つまり,第三正規形までは更新不整合を防げる可能性を高めると同時に従属性も保存することができるという関係になっていますが,ボイス・コッド正規形以降は従属性保存を犠牲にして更新不整合を防げる可能性を高めていくというトレードオフになっています。なお,全ての正規形には無損失結合分解が得られるアルゴリズムが存在します。
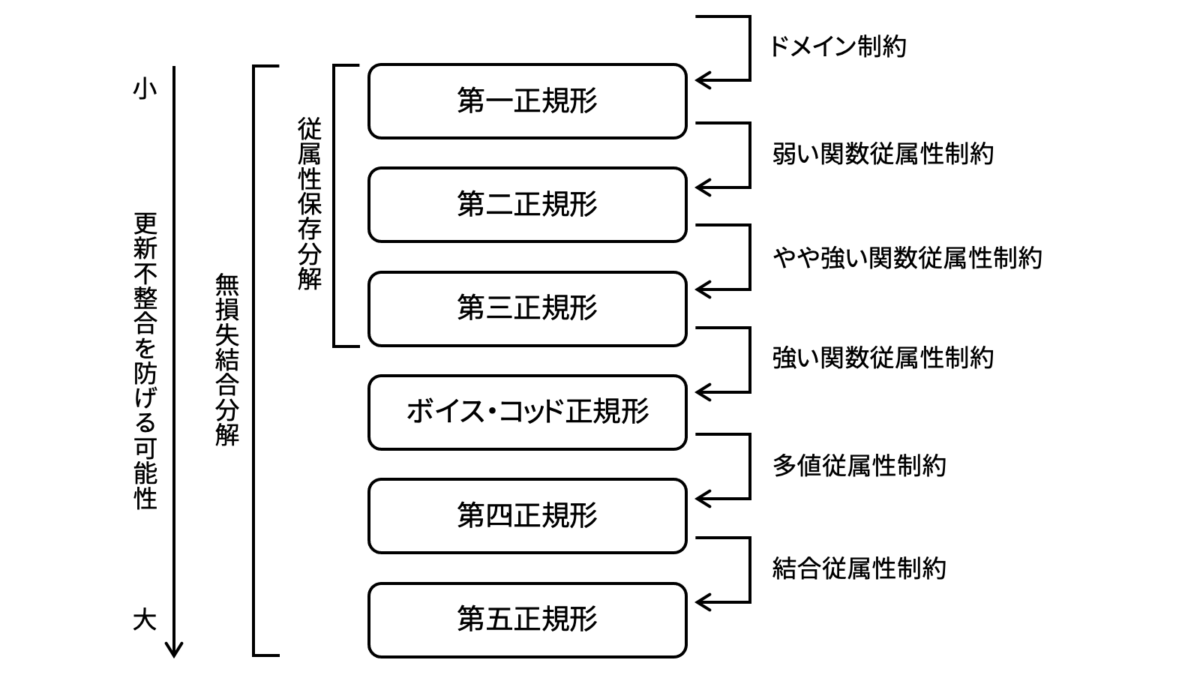
各種制約と正規形の定義については後ほど確認します。
多くのリレーションスキーマは,第三正規形に変形した時点でボイス・コッド正規形・第四正規形・第五正規形の定義を満たす形になっていることがほとんどです。というのも,ボイス・コッド正規形・第四正規形・第五正規形は重箱の隅を突くような細かな制約を考慮するものであり,論述的にリレーションスキーマの正規化を語る上で必要となる道具として持ち出された概念になります。したがって,データベースの運用上は第三正規形までをおさえておけば十分でしょう。ただし,本稿では正規形に関する正確な記述を行うため,ボイス・コッド正規形以降もスコープとします。
第二正規形は第三正規形への中間的な状態という位置づけであるため,第二正規形自体には大きな意義はありません。前述の通り,第三正規形を満たした時点でボイス・コッド正規形以降の制約を満たしている場合がほとんどであること,そしてボイス・コッド正規形への変形が必ずしも従属性保存分解でないことを踏まえると,データベース設計の目的はあくまでも第三正規形を目指すことだといえます。
各種正規形の定義
それぞれの正規形の定義とその例を確認していきます。表記を簡潔にするため,特に断わりなく以下のノーテーションを利用します。
| ノーテーション | 意味 |
|---|---|
| $RS$ | リレーションスキーマ |
| $X$ | $X\subseteq RS$なる属性 |
| $A$ | $A\subseteq RS$かつ$A\notin X$なる属性 |
| $Y$ | $XY\subseteq RS$かつ$Y\notin X$ |
| $X\rarr A$ | 関数従属性 |
$A$や$Y$に$X$の部分集合ではないという条件がないと,自明な関数従属性や自明な多値従属性を含んでしまうノーテーションとなってしまいます。
第一正規形
$RS$のドメインが分解不可能な単純値のみで構成されるという制約を第一正規形制約と呼ぶ。$RS$が第一正規形制約を満たすとき,$RS$は第一正規形であるという。
第一正規形の英語表記はfirst formですので,1NFと略されます。また,第一正規形制約を満たさないリレーションスキーマを非正規リレーションと呼びます。1NFを一言で表すならば「セルの結合がない」です。
定義を噛み砕くと,セルが結合されていない表のみで構成されているリレーションスキーマを第一正規形と呼ぶということです。逆に言えば,結合されたセルが存在する場合は第一正規形制約を満たさないということになります。第一正規形制約は,ドメインの取りうる値を複数値の集合ではなく単純値とするドメイン制約の一種と捉えることができ,リレーショナルデータモデルにおいて表・行・列の統一的な扱いを可能にするための基礎的な制約となっています。
第一正規形を求める手順
セルを分割すればよいです。
例
以下のリレーションは第一正規形制約を満たしていません。
| 科目番号 | 科目名 | 単位数 | 担当者 | 実習課題 | |
|---|---|---|---|---|---|
| 担当者名 | 課題番号 | 課題名 | |||
| 001 | データベース | 2 | 山田 | 01 | モデリング |
| 鈴木 | 02 | 設計 | |||
| NULL | 03 | SQL | |||
| 002 | システムプログラム | 3 | 佐藤 | 01 | C言語 |
| 田中 | 02 | OS | |||
以下のように変形すると,第一正規形制約を満たします。
| 科目番号 | 科目名 | 単位数 | 担当者名 | 課題番号 | 課題名 |
|---|---|---|---|---|---|
| 001 | データベース | 2 | 山田 | 01 | モデリング |
| 001 | データベース | 2 | 鈴木 | 02 | 設計 |
| 001 | データベース | 2 | NULL | 03 | SQL |
| 002 | システムプログラム | 3 | 佐藤 | 01 | C言語 |
| 002 | システムプログラム | 3 | 田中 | 02 | OS |
第二正規形
第二正規形の英語表記はsecond formですので,2NFと略されます。前述の通り,2NFは3NFへの中間的な状態という位置づけであるため,2NF自体には大きな意義はありません。2NFを一言で表すならば「属性間の依存関係に弱い制約を課している」です。この条件は「部分関数従属性の排除」や「完全関数従属性を満たす」と表現される場合もあります。
第二正規形を求める手順
第三正規形を求める手順に従えばよいです。
例
第三正規形の例で第二正規形についても扱います。
第三正規形
第三正規形の英語表記はthird formですので,3NFと略されます。第二正規形制約との違いは条件1.です。第二正規形制約では候補キーの真部分集合であれば満たされていたものを,第三正規形制約では超キーでなくてはならず,制約が強められていることが分かります。また,定義では全ての関数従属性に対して条件を満たすとされていますが,実際にはアームストロングの公理系と呼ばれる公理により,極小被覆から全ての関数従属性を導出できることが知られていますので,3NFの判定には極小被覆に含まれる関数従属性だけを確認すれば十分です。3NFを一言で表すならば「属性間の依存関係にやや強い制約を課している」です。
第三正規形を求める手順
下記のアリゴリズムにより,従属性保存分解かつ無損失結合分解として第三正規形制約を満たす分解を求められることが知られています。
# 変数初期化
rho := {空集合} # 結果を返すリレーションスキーマの集合
M := {Fの極小被覆} # 検査対象の関数従属性
# 既にRSが第三正規形である場合はRSを返す
if { XA=RS なる X->A が存在} rho := {RS}
# RSが第三正規形でない場合は関数従属性ごとに新しいリレーションスキーマを作成
else
for each X->A in M
rho := rho || {XA} # 結果を返す変数に関数従属性ごとにリレーションスキーマを格納
M := M - {X->A} # 検査が完了した関数従属性は検査対象の変数から削除
# 得られたリレーションスキーマの中に元のリレーションスキーマの候補キーがない場合は無理やり追加する
if {全てのrhoの要素がRSの候補キーを含まない} rho := rho || {Rの任意の候補キー}このアルゴリズムでは「既にRSが第三正規形であるか」の判定に,極小被覆の関数従属性の中にリレーション全体を表現可能な関数従属性が含まれているかというロジックを使っています。厳密には証明が必要なのですが,直感的にも,ある関数従属性によりリレーション全体が表現可能であれば,その関数従属性の根本は候補キーとなりますので,第三正規形制約の定義を満たすことが分かります。
例
表形式の例と記号形式の例の二つを考えます。
表形式の例
表形式の例として,以下のリレーションを考えます。
| 商品番号 | 顧客番号 | 社員番号 | 販売価格 |
|---|---|---|---|
| $i1$ | $c1$ | $s1$ | $100$ |
| $i1$ | $c2$ | $s2$ | $120$ |
| $i2$ | $c1$ | $s1$ | $200$ |
| $i2$ | $c2$ | $s2$ | $210$ |
| $i3$ | $c1$ | $s1$ | $250$ |
| $i3$ | $c2$ | $s2$ | $250$ |
| $i4$ | $c1$ | $s1$ | $150$ |
営業リレーションには,{{商品番号,顧客番号}$\rarr$販売価格}と{顧客番号$\rarr$社員番号}という二つの関数従属性があります。これは極小被覆です。関数従属性における矢印の根本を定めれば全ての属性が定まることが分かりますので,営業リレーションの超キーは{商品番号,顧客番号}となりますので,この場合は超キーは候補キーにもなります。したがって,素属性は{商品番号}と{顧客番号}の二つになります。
{商品番号,顧客番号$\rarr$販売価格}に関して,{商品番号,顧客番号}は超キーではありませんし,{販売価格}も素属性ではありません。{顧客番号$\rarr$社員番号}に関して,{顧客番号}は超キーではありませんし,{社員番号}も素属性ではありません。したがって,営業リレーションは第三正規形制約を満たしません。一方で,{顧客番号}は候補キーの一部であるため,{{商品番号,顧客番号}$\rarr$販売価格}と{顧客番号$\rarr$社員番号}のいずれも第二正規形制約を満たします。したがって,営業リレーションは第二正規形ではありますが,第三正規形ではないリレーションの例となります。
上のアルゴリズムに則ると,以下のようにリレーションスキーマを分解できます。
| 商品番号 | 顧客番号 | 販売価格 |
|---|---|---|
| $i1$ | $c1$ | $100$ |
| $i1$ | $c2$ | $120$ |
| $i2$ | $c1$ | $200$ |
| $i2$ | $c2$ | $210$ |
| $i3$ | $c1$ | $250$ |
| $i3$ | $c2$ | $250$ |
| $i4$ | $c1$ | $150$ |
| 顧客番号 | 社員番号 |
|---|---|
| $c1$ | $s1$ |
| $c2$ | $s2$ |
左側のリレーションが営業リレーションの超キー{商品番号,顧客番号}を含みますので,候補キーから構成されるリレーションを無理やり付け加える必要はありません。また,{顧客番号$\rarr$社員番号}という関数従属性に注目すると,無損失結合分解の必要十分条件より,この分解は無損失結合分解であることも分かります。
左側のリレーションには,{{商品番号,顧客番号}$\rarr$ 販売価格}という関数従属性があります。これは極小被覆です。関数従属性における矢印の根本を定めれば全ての属性が定まることが分かりますので,左側のリレーションの超キーは{商品番号,顧客番号}となります。ただし,この場合は超キーは候補キーにもなりますので,素属性は{商品番号}と{顧客番号}の二つになります。{{商品番号,顧客番号}$\rarr$ 販売価格}に関して,{商品番号,顧客番号}は超キーとなりますので,左側のリレーションは第三正規形制約を満たします。
右側のリレーションには,{顧客番号$\rarr$ 社員番号}という関数従属性があります。これは極小被覆です。関数従属性における矢印の根本を定めれば全ての属性が定まることが分かりますので,左側のリレーションの超キーは{顧客番号}となります。ただし,この場合は超キーは候補キーにもなりますので,素属性は{顧客番号}の二つになります。{顧客番号$\rarr$ 社員番号}に関して,{顧客番号}は超キーとなりますので,右側のリレーションは第三正規形制約を満たします。
記号形式の例
記号形式の例として,$RS=\{I,A,S,P\}$および$F=\{IA\rarr S,I\rarr P,S\rarr A\}$という関数従属性集合を考えます。まず,以下のような図で関数従属性における矢印の根本を考えることにより,超キーが$\{IA, IS\}$であることが分かります。
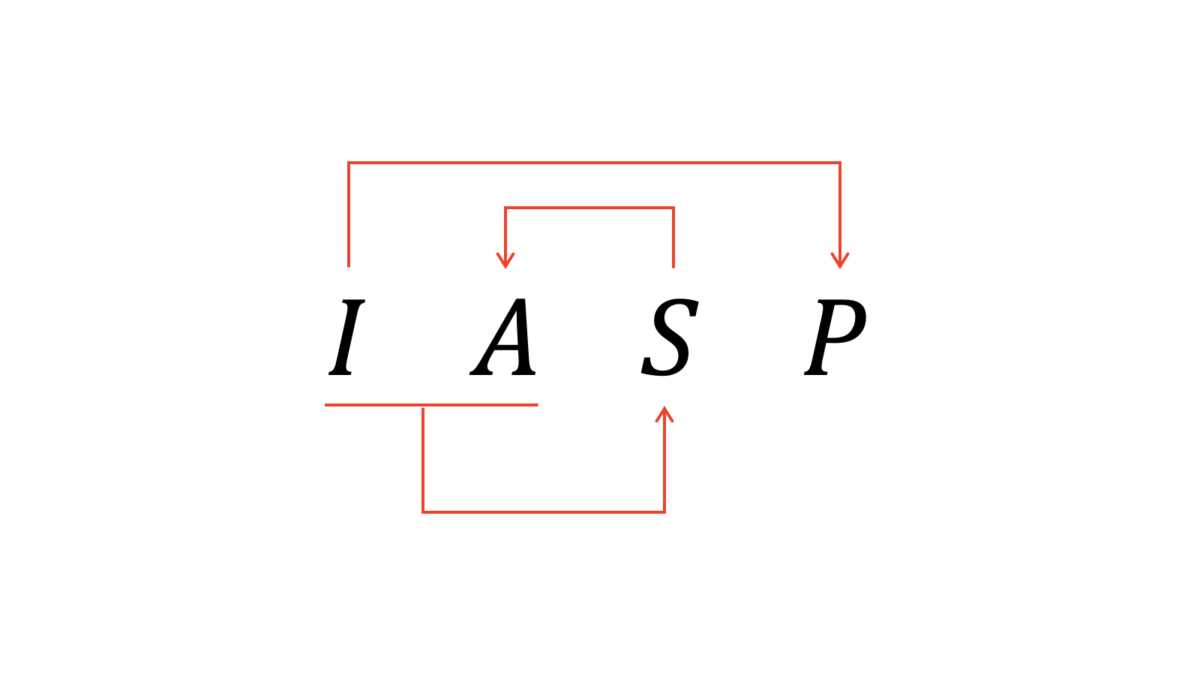
候補キーとして$\{IS\}$が含まれることを忘れないようにしてください。
初期状態では,$I\rarr P$に関して,$I$は候補キーではありませんし,$P$も素属性ではありません。したがって,$RS$は第三正規形制約を満たしません。
上のアルゴリズムに則ると,$\{IAS,IP,AS\}$という新たなリレーションスキーマが三つ得られます。$AS$は$IAS$の部分集合であるため,本質的には$\{IAS,IP\}$の二つのリレーションスキーマを考えれば十分です。$IAS$が元のリレーションの超キー$\{IA\}$もしくは$\{IS\}$を含みますので,候補キーから構成されるリレーションを無理やり付け加える必要はありません。また,$I\rarr P$という関数従属性に注目すると,無損失結合分解の必要十分条件より,この分解は無損失結合分解であることも分かります。
新しいリレーションスキーマ$IAS$には,$IA\rarr S$と$S\rarr A$という関数従属性があります。これは極小被覆です。関数従属性における矢印の根本$IA$を定めれば全ての属性が定まるのと,$S$に加えて$I$を定めれば全ての属性が定まることが分かりますので,$IAS$の超キーは$IA$または$IS$となります。ただし,この場合は超キーは候補キーにもなりますので,素属性は$I,A,S$となります。$IA\rarr S$に関して,$IA$は超キーとなりますので,第三正規形制約を満たします。$S\rarr A$に関して,$S$は超キーとなりますので,第三正規形制約を満たします。以上より,$IAS$は第三正規形制約を満たします。
新しいリレーションスキーマ$IP$には,$I\rarr P$という関数従属性があります。これは極小被覆です。関数従属性における矢印の根本$I$を定めれば全ての属性が定まるのことが分かりますので,$IP$の超キーは$I$となります。ただし,この場合は超キーは候補キーにもなりますので,素属性は$I$となります。$I\rarr P$に関して,$I$は超キーとなりますので,第三正規形制約を満たします。$S\rarr A$に関して,$S$は超キーとなりますので,第三正規形制約を満たします。したがって,$IP$は第三正規形制約を満たします。
いずれの新しいリレーションスキーマも第三正規形制約を満たしますので,$\{IAS,IP\}$という分解は第三正規形となります。
ボイス・コッド正規形
全ての関数従属性$X\rarr A$に対し,$X$が$RS$の超キーであるという制約をボイス・コッド正規形制約という。$RS$がボイス・コッド正規形制約を満たすとき,$RS$はボイス・コッド正規形であるという。
ボイス・コッド正規形の英語表記はBoyce-Codd normal formですので,BCNFと略されます。BCNFの制約条件は,第三正規形の条件2.を排除したものになっています。また,定義から分かる通り,二つの属性から構成されるリレーションは,考え得る関数従属性は二つしかなく,それぞれ必ず$X$は超キーとなりますので,必ずBCNFになります。BCNFを一言で表すならば「属性間の依存関係に強い制約を課している」です。上記の条件は「推移的関数従属性の排除」と表現される場合もあります。
ボイス・コッド正規形を求める手順
下記のアリゴリズムにより,無損失結合分解としてボイス・コッド正規系制約を満たす分解を求められることが知られています。
# 変数初期化
rho := {空集合} # 結果を返すリレーションスキーマの集合
# ボイス・コッド正規形制約に違反する関数従属性がなくなるまで繰り返す
while {rhoにBCNFでないリレーションスキーマRSが存在}
for each {BCNFでないRSの関数従属性 X->A}
rho := (rho - RS) || {RS - A} || XA # 無損失結合分解となるように関数従属性をブチっと切る
{{RS - A}の関数従属性の射影と{XA}の関数従属性の射影を計算して次の判定に備える}このアルゴリズムで行っているのは「ボイス・コッド正規形制約に違反する関数従属性がなくなるまで関数従属性を切って新しいリレーションスキーマを作成する」という操作です。最終的には,全てのリレーションスキーマは要素数が$2$となりますので,前述の通り必ずボイス・コッド正規形制約を満たすことが保証されています。また,for eachの中で無損失結合分解の必要十分条件を満たすような分解を行っていますので,このアルゴリズムに則って得られる分解は無損失結合分解となることが分かります。
例
第三正規形の例を利用します。正規化前は第三正規形ではありませんでしたので,ボイス・コッド正規形でもありません。上のアルゴリズムに則ると,下図のようにリレーションスキーマを分解していくことができます。
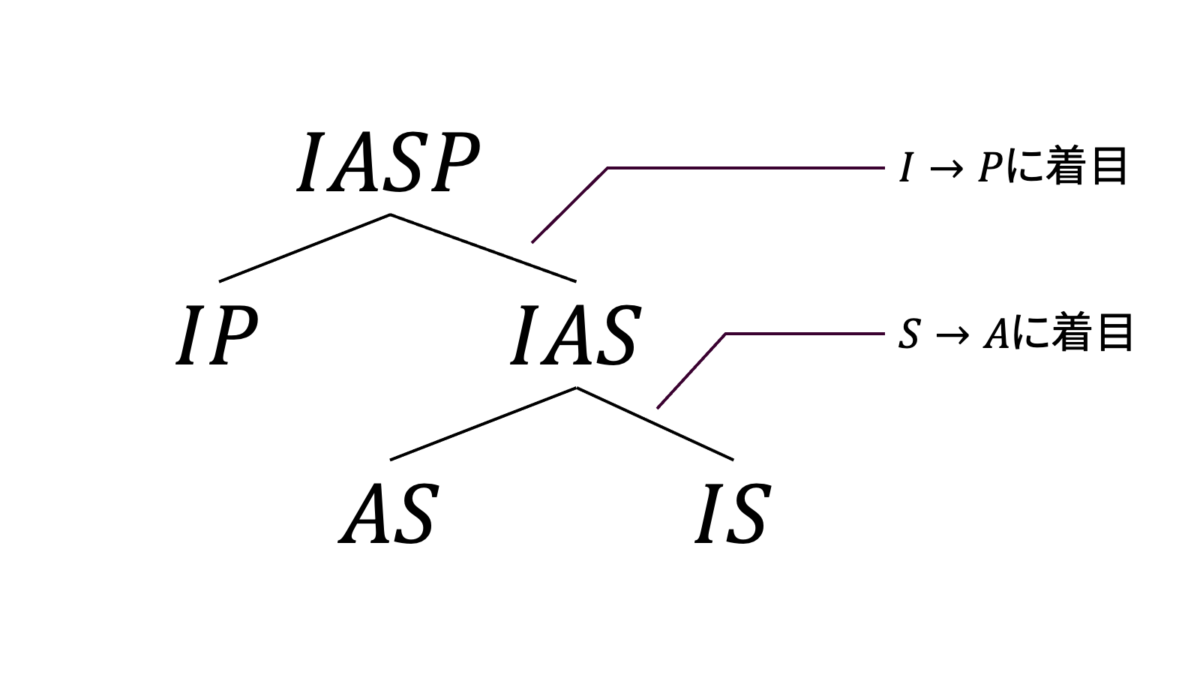
ただし,最初に$\{I\rarr P\}$ではなく$\{S\rarr A\}$に着目すると,下図のようにリレーションスキーマを分解していくことができます。いずれの分解も,最終的には要素数が$2$となっているため,ボイス・コッド正規形であることが分かります。
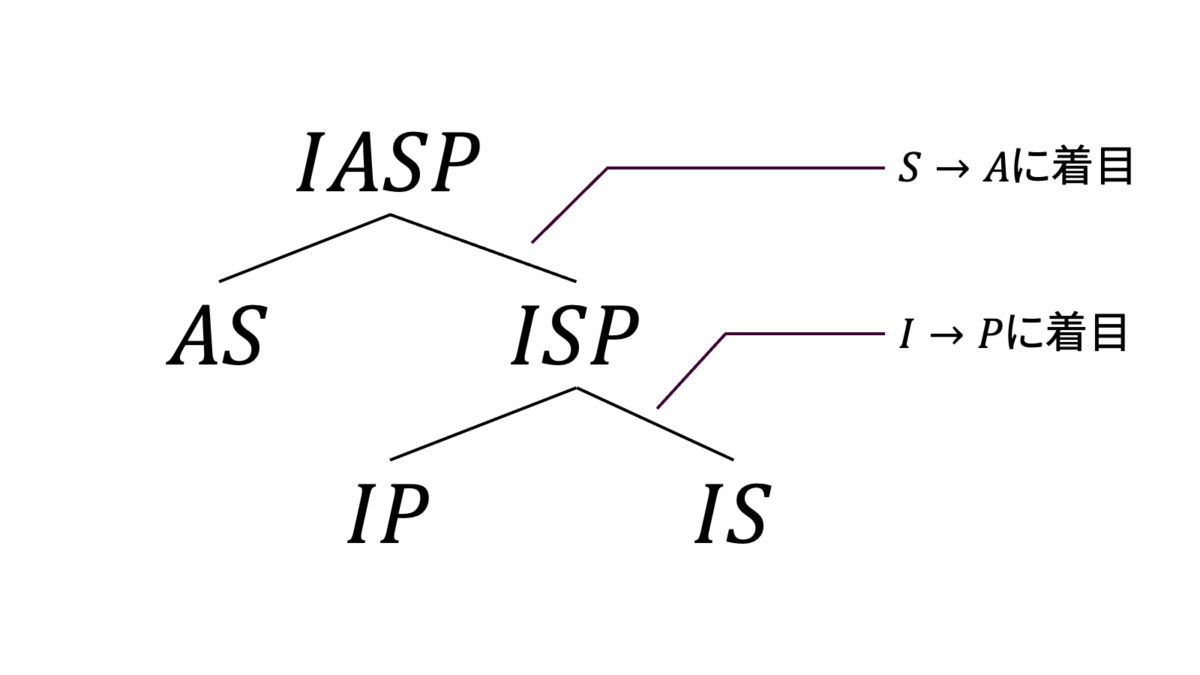
今回はたまたま同じ結果が得られましたが,一般的に着目する関数従属性の順番に依存して得られるボイス・コッド正規形の分解は異なります。
第四正規形
第四正規形の英語表記はfourth normal formですので,4NFと略されます。4NFの制約条件は,ボイス・コッド正規形の条件における関数従属性を多値従属性に拡張したものになっています。4NFを一言で表すならば「タスキ掛けのような明らかな冗長性がない」です。
第四正規形を求める手順
ボイス・コッド正規系を求める手順において,関数従属性を多値従属性に置き換えます。
無損失結合分解の必要十分条件を多値従属性に拡張することで,ボイス・コッド正規形を求める手順の関数従属性をを多値従属性に拡張した手順でも無損失結合分解が得られることが保証されます。
例
以下のリレーションを利用します。
| プロジェクト番号 | 社員番号 | ミーティング日 |
|---|---|---|
| $p_{1}$ | $e_{1}$ | 月 |
| $p_{1}$ | $e_{2}$ | 月 |
| $p_{1}$ | $e_{1}$ | 木 |
| $p_{1}$ | $e_{2}$ | 木 |
| $p_{2}$ | $e_{1}$ | 月 |
| $p_{2}$ | $e_{3}$ | 月 |
| $p_{2}$ | $e_{1}$ | 金 |
| $p_{2}$ | $e_{3}$ | 金 |
この例からも分かる通り,第四正規形を満たさないリレーションは明らかに不自然なリレーションであることがほとんどです。冒頭からお伝えしていますが,ほとんどのリレーションは第三正規形を目指せば自然にボイス・コッド正規形以降の制約も満たしますので,第四正規形以降の議論は重箱の隅をつつくような内容になります。
このリレーションには,関数従属性が存在しません。ゆえに,超キーは全ての属性で{プロジェクト番号,社員番号,ミーティング日}となります。さらに,ボイス・コッド正規系制約を違反する関数従属性も存在しませんので,このリレーションはボイス・コッド正規系となります。
一方,多値従属性の定義でもお伝えしている通り,このリレーションには{プロジェクト番号$\twoheadrightarrow$社員番号}と{プロジェクト番号$\twoheadrightarrow$ミーティング日}という二つの多値従属性が存在します。いずれの多値従属性についてもプロジェクト番号は超キーではありませんので,このリレーションは第四正規形ではありません。
プロジェクト番号を$P$,社員番号を$S$,ミーティング日を$M$とおきます。ボイス・コッド正規形を求める手順と同様に分解を行うと,下図のように分解できます。
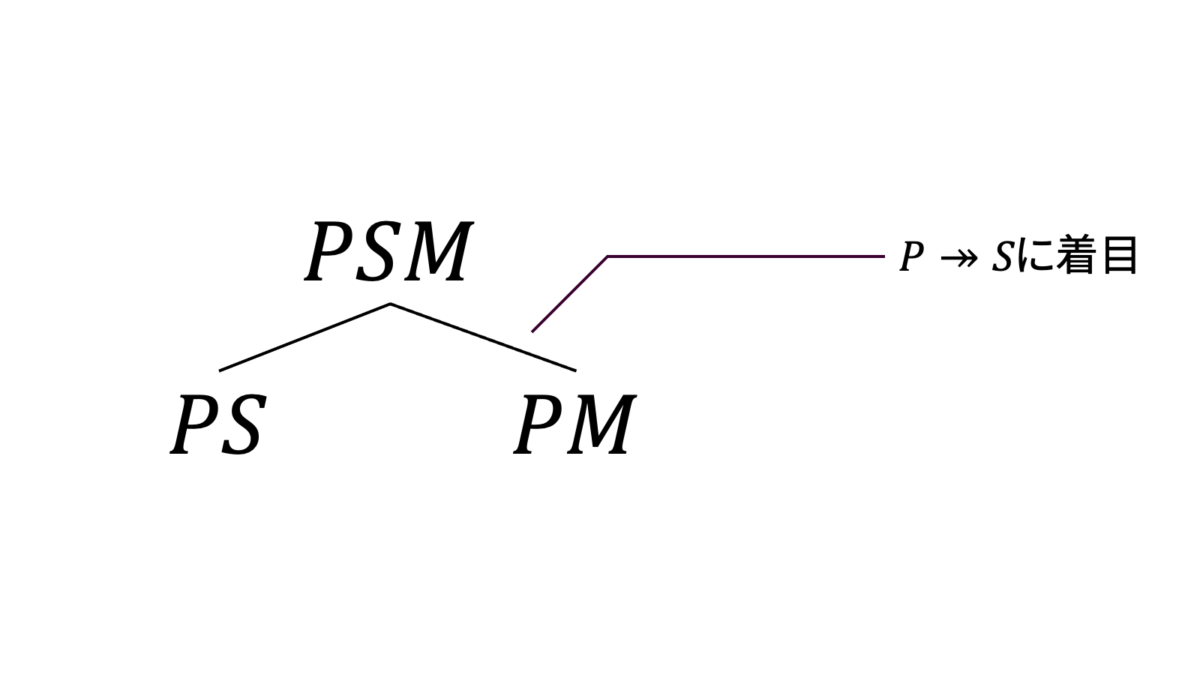
ボイス・コッド正規形での分解と同様に,$P\twoheadrightarrow M$から着目しても構いませんが,今回の例も全く同様の分解が得られます。
分解後の$\{P,S\}$と$\{P,M\}$は,以下のようになります。
| プロジェクト番号 | 社員番号 |
|---|---|
| $p_{1}$ | $e_{1}$ |
| $p_{1}$ | $e_{2}$ |
| $p_{2}$ | $e_{1}$ |
| $p_{2}$ | $e_{3}$ |
| プロジェクト番号 | ミーティング日 |
|---|---|
| $p_{1}$ | 月 |
| $p_{1}$ | 木 |
| $p_{2}$ | 月 |
| $p_{2}$ | 金 |
いずれのリレーションについても多値従属性は存在しませんので,第四正規形制約を違反する多値従属性も存在しません。したがって,分解後のリレーションはいずれも第四正規形になります。
第五正規形
自明でない結合従属性$\ast(RS_{1},{\cdots},RS_{n})$が成り立つならば$RS_{1},{\cdots},RS_{n}$は常に$RS$の超キーであるという制約を第五正規形制約という。$RS$が第五正規形制約を満たすとき,$RS$は第五正規形であるという。
第五正規形(fifth normal form)は射影結合正規形(projection join normal form)とも呼ばれ,頭文字を取って5NFやPJNFと略されます。結合従属性が多値従属性の一般化であることを踏まえると,第五正規形は第四正規形制約を守りながら制約をより強くした正規形であることが分かります。第五正規形に明示的に変形する必要がある場合は,「違和感の覚えるリレーションスキーマではないが,無損失結合分解となるように複数のリレーションスキーマに分けてあげた方が更新不整合を起こす可能性が低くなりそうだ」といったようなリレーションスキーマであることがほとんどです。5NFを一言で表すならば「複数の表の結合として分解不可能な最小単位である」です。
第五正規形を求める手順
第五正規形に違反する結合従属性に基づいて分解を行えばよいです。第四正規形までとは異なり,結合従属性を判定するために分解後の形を調べる必要があるという特殊な正規形になっています。
例
以下のリレーションを利用します。
| 工場番号 | 部品番号 | 業者番号 |
|---|---|---|
| $f_{1}$ | $p_{1}$ | $s_{1}$ |
| $f_{1}$ | $p_{2}$ | $s_{1}$ |
| $f_{1}$ | $p_{2}$ | $s_{2}$ |
| $f_{1}$ | $p_{3}$ | $s_{2}$ |
| $f_{2}$ | $p_{1}$ | $s_{1}$ |
| $f_{2}$ | $p_{3}$ | $s_{3}$ |
このリレーションには多値従属性が存在しませんので,第四正規形制約を満たさない多値従属性も存在しません。したがって,このリレーションは第四正規形です。多値従属性が存在しませんので,このリレーションの超キーは全ての属性となり,{工場番号,部品番号,業者番号}です。
一方,{{工場番号,部品番号},{工場番号,業者番号},{部品番号,業者番号}}の三つのリレーションスキーマへの分解を考えます。
| 工場番号 | 部品番号 |
|---|---|
| $f_{1}$ | $p_{1}$ |
| $f_{1}$ | $p_{2}$ |
| $f_{1}$ | $p_{3}$ |
| $f_{2}$ | $p_{1}$ |
| $f_{2}$ | $p_{3}$ |
| 工場番号 | 業者番号 |
|---|---|
| $f_{1}$ | $s_{1}$ |
| $f_{1}$ | $s_{2}$ |
| $f_{2}$ | $s_{1}$ |
| $f_{2}$ | $s_{3}$ |
| 部品番号 | 業者番号 |
|---|---|
| $p_{1}$ | $s_{1}$ |
| $p_{2}$ | $s_{1}$ |
| $p_{2}$ | $s_{2}$ |
| $p_{3}$ | $s_{2}$ |
| $p_{3}$ | $s_{3}$ |
これらの自然結合は元のリレーションスキーマと完全一致しますので,結合従属性が成り立ちます。各分解の属性は元のリレーションスキーマの超キーとなっていませんので,上のリレーションスキーマは第五正規形ではありません。分解後の各リレーションスキーマでは,自明な結合従属性は成り立ちませんので,分解後のリレーションスキーマは第五正規形になります。



コメント