本記事は「これなら分かる!はじめての数理統計学」シリーズに含まれます。
不適切な内容があれば,記事下のコメント欄またはお問い合わせフォームよりご連絡下さい。
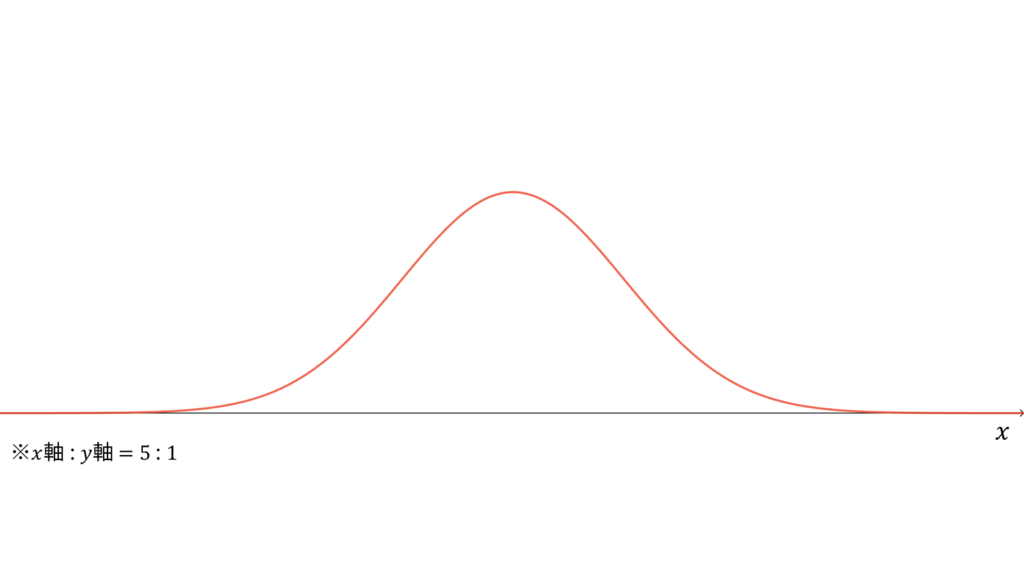
標準正規分布
f_{X}(x) &= \frac{1}{\sqrt{2\pi}}\exp\left( -\frac{1}{2} x^2 \right) \\[0.7em]
M_{X}(t) &= \exp \left(\frac{1}{2}t^2 \right) \\[0.7em]
E[X] &= 0 \\[0.7em]
V[X] &= 1
\end{align}
正規分布$\N (\mu, \sigma^2)$に従う確率変数$X$対して,
Z &= \frac{X-\mu}{\sigma}
\end{align}
が従う分布$\N (0, 1)$を標準正規分布と呼びます。標準正規分布に従う確率変数$X$に対し,実現値は
x \in \bbR
\end{align}
であり,モーメント母関数の変数は$t \in \bbR$とします。標準分布は再生性を持ち,ロードマップ中では正規分布を標準化したもの相当します。
確率密度関数
正規分布$\N (\mu, \sigma^2)$に従う確率変数を$X$とおきます。このとき,以下で定義される確率変数
Z&=\frac{X-\mu}{\sigma}
\end{align}
を考えます。$Z$は$X$に対する定数の引き算と割り算で定義されていますので,$Z$が従う分布は$X$と同じで正規分布になります。そこで,確率変数の性質を利用して,$Z$の従う正規分布の期待値を計算してみましょう。
E[Z] &= E\left[ \frac{X-\mu}{\sigma} \right] \\[0.7em]
&= \frac{E[X]-\mu}{\sigma} \\[0.7em]
&= \frac{\mu-\mu}{\sigma} \\[0.7em]
&= 0
\end{align}
同様に,分散を計算しましょう。ただし,分散の演算子$V$は期待値の演算子$E$とは異なり線形性を持たないことに注意してください。今回は,定数の引き算ですので,共分散は$0$になります。
V[Z] &= V\left[ \frac{X-\mu}{\sigma} \right] \\[0.7em]
&= \frac{V[X]+0-0}{\sigma^2} \\[0.7em]
&= \frac{\sigma^2}{\sigma^2} \\[0.7em]
&= 1
\end{align}
したがって,$Z$は平均が$0$で分散が$1$の正規分布に従います。
Z \sim \N (0, 1)
\end{align}
この$\N (0, 1)$を標準正規分布と呼びます。確率密度関数は,正規分布で$\mu=0$かつ$\sigma^2=1$の場合を考えればよいです。
f(x) &= \frac{1}{\sqrt{2\pi}} e^{-x^2/2}
\end{align}
正規分布のページでは正規分布を「二項分布の極限としての証明」と「ガウスによる証明」の2通りで導出しています。また,ポアソン分布のページではポアソン分布の極限が正規分布になることを示しています。
モーメント母関数
$\mu=0$かつ$\sigma=1$を正規分布のモーメント母関数に代入すればよいです。
M(t) &= e^{t^2/2}
\end{align}
平均・分散
$\mu=0$かつ$\sigma=1$を正規分布の平均・分散に代入すればよいです。
E[X] &= 0 \\[0.7em]
V[X] &= 1
\end{align}
再生性
再生性を示すためには,再生性を示したい分布に従う独立な二つの確率変数を考え,その和のモーメント母関数を計算したときに,パラメータが和の形になっていることを示します。ただし,正規分布が再生性を持ちますので,その特殊な場合の標準正規分布も再生性を持ちます。
ロードマップ
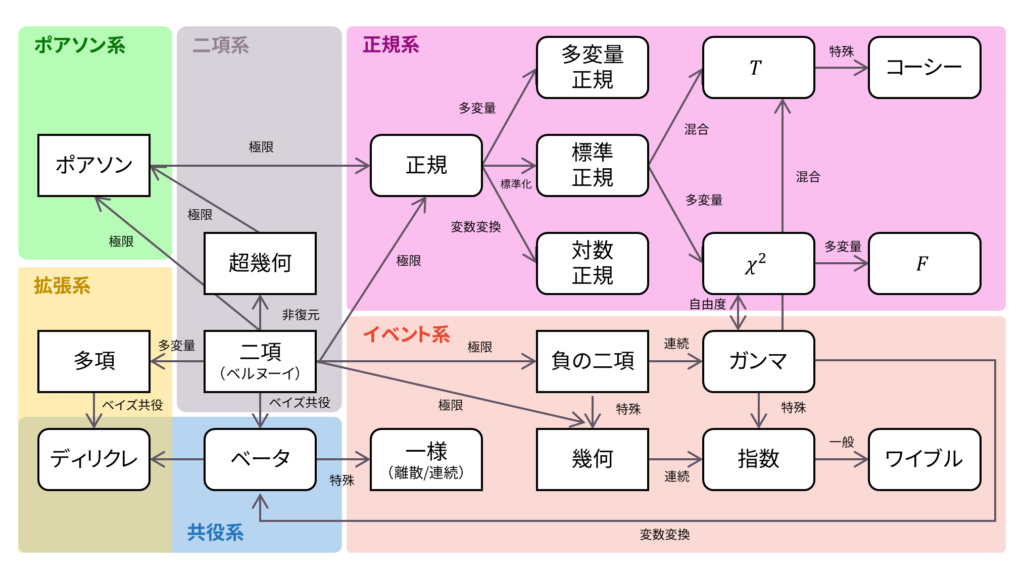
さて,ロードマップに戻りましょう。 標準正規分布は,正規分布を標準化して得られる確率分布でした。以下の内容も参考になるでしょう。
参考文献
本稿の執筆にあたり参考にした文献は,以下でリストアップしております。


コメント