本記事は「これなら分かる!はじめての数理統計学」シリーズに含まれます。
不適切な内容があれば,記事下のコメント欄またはお問い合わせフォームよりご連絡下さい。
多項分布
f_{\mX}(\vx) &= \frac{n!}{x_1!\cdots x_K!}~p_1^{x_1}\cdots p_K^{x_K} \\[0.7em]
G_{\mX}(\vs) &= (p_1s_1 + \cdots + p_{K-1}s_{K-1} + p_K)^n \\[0.7em]
E[X_i] &= np_i \\[0.7em]
V[X_i] &= np_i(1-p_i)
\end{align}
二項分布を$n$カテゴリに拡張した分布を多項分布と呼びます。ただし,毎回の試行で各カテゴリーの発生確率を$p_1,\cdots,p_K$とし,これらは
p_1+\cdots+p_K &= 1
\end{align}
を満たします。パラメータ$n,p_{1},\ldots,p_{K}$の多項分布は
\Mn(n,p_{1},\ldots,p_{K})
\end{align}
と表されます。$K-1$個の確率が決まった時点であと$1$つの確率も決まってしまうため,自由に定められる確率変数は$X_1,\ldots, X_{K-1}$の$K-1$個になります。また,多項分布では実現値$x$と確率母関数の変数$s$も$K-1$個用意しなくてはなりません。簡単のため,確率質量関数と確率母関数は,以下の長さ$K$のベクトルを用いて表します。
\mX &= [ X_1, \ldots, X_K ] \\[0.7em]
\vx &= [x_1, \ldots, x_K] \\[0.7em]
\vs &= [s_1, \ldots, s_K]
\end{align}
ただし,自由度は$K-1$であることに注意してください。多項分布に従う確率変数$X_k$に対し,実現値は
x_k \in \{0, \ldots, n\}
\end{align}
であり,確率母関数の変数は$|s_k|\leq 1$とします。多項分布は再生性を持たず,ロードマップ中では二項分布の多変量拡張に相当します。
確率密度関数
二項分布を複数のカテゴリに拡張した分布が多項分布です。多項分布の確率密度関数は直感的に導くことが可能です。カテゴリ$i$が$x_i$回独立に起こるとすれば,考えられる組み合わせは$n!$で,全事象は$x_1!\cdots x_K!$です。確率部分は$p_1^{x_1}\cdots p_K^{x_K}$となり,たしかに以下のように確率密度関数が求められます。
f_{\mX}(\vx) &= \frac{n!}{x_1!\cdots x_K!}~p_1^{x_1}\cdots p_K^{x_K}
\end{align}
確率母関数
確率母関数の定義に従って計算していき,多項定理を利用します。注意するべきなのは,多項分布では
x_1 + \cdots + x_K &= n\label{制約条件}
\end{align}
という条件があるため,対象とする確率変数は$x_1,\cdots, x_{K-1}$の$K-1$個になるという点です。$K-1$個の確率が決まった時点であと1つの確率も決まってしまうからです。また,今までは確率母関数の$s$は1つでしたが,多項分布では$K-1$個の$x$を考えるため,$s$も$K-1$個用意すれば十分です。
G_{\mX}(\vs) &= E[s_1^{x_1}\cdots s_{K-1}^{x_{K-1}}] \\[0.7em]
&= \sum_{\vx\in A} \frac{n!}{x_1!\cdots x_K!}~(p_1s_1)^{x_1}\cdots (p_{K-1}s_{K-1})^{x_{K-1}} (p_K)^{x_K} \label{1}\\[0.7em]
&= (p_1s_1 + \cdots + p_{K-1}s_{K-1} + p_K)^n \label{2}
\end{align}
ただし,式($\ref{制約条件}$)を満たす$x_{1}\ldots, x_{K}$の集合を$A$とおき,式($\ref{1}$)から式($\ref{2}$)は多項定理を利用しました。
平均・分散
離散分布の平均と分散を求めるためには,確率母関数の性質を利用します。しかし,多項分布の平均と分散は二項分布の定義を利用すると簡単に求められます。そのためには,まず多項分布のある1つの変数に関する周辺分布が二項分布になることを示さなくてはなりません。
多項関数の確率母関数において,1つの変数$x_i$に着目して確率母関数を求めます。そのためには,$s_i$以外の$s$を全て1にセットすればよいです。なぜなら,多変量の確率母関数は$E[s_{1}^{x_{1}}\cdots s_{K}^{x_{K}}]$と表されるため,ある$x_{i}$に対する確率母関数$E[s_{1}^{x_{1}}]$を求めたい場合は$s_{1}{=}\cdots{=}s_{i-1}{=}s_{i+1}\cdots{=}s_{K}{=}1$とできるからです。すると,
G_{\mX}(\vs) &= (p_1 + \cdots + p_is_i + \cdots + p_{K-1} + p_K)^n \\[0.7em]
&= (p_is_i + 1 - p_i)^n
\end{align}
となり,二項分布の確率母関数と一致します。したがって,多項分布におけるある1つの変数の周辺分布は二項分布になることが分かりました。ゆえに,$X=X_1+\cdots+X_{K-1}$として$X$が多項分布にしたがうとき,以下が成り立ちます。
X_{i} \sim B(n, p_i) \\[0.7em]
X_{j} \sim B(n, p_j)
\end{align}
新しい確率変数$X_{i}+X_{j}$は試行回数$n$,出現確率$p_{i}+p_{j}$の二項分布に従います。すなわち,
X_i + X_j \sim B(n, p_1 + p_j)
\end{align}
と表されます。ここで,確率変数の性質より
V[X_i + X_j]=V[X_i] + V[X_j] + 2\Cov[X_i, X_j]
\end{align}
が成り立つことに注意すると,$X_i$の期待値・分散,$X_i$と$X_j$の共分散は以下のように求められます。
E[X_i] &= n p_i \\[0.7em]
V[X_i] &= n p_i (1 - p_i) \\[0.7em]
\Cov[X_i, X_j] &= \frac{V[X_i + X_j] - V[X_i] - V[X_j]}{2} \\[0.7em]
&= \frac{n (p_i + p_j)(1 - p_i - p_j) - n p_i (1 - p_i) - n p_j (1 - p_j)}{2} \\[0.7em]
&= -n p_i p_j
\end{align}
ただし,二項分布の平均と分散を利用しました。
再生性
再生性を示すためには,再生性を示したい分布に従う独立な二つの確率変数を考え,その和の確率母関数を計算したときに,パラメータが和の形になっていることを示します。しかし,確率母関数の形からも推測される通り,多項分布は再生性を持ちません。
ロードマップ
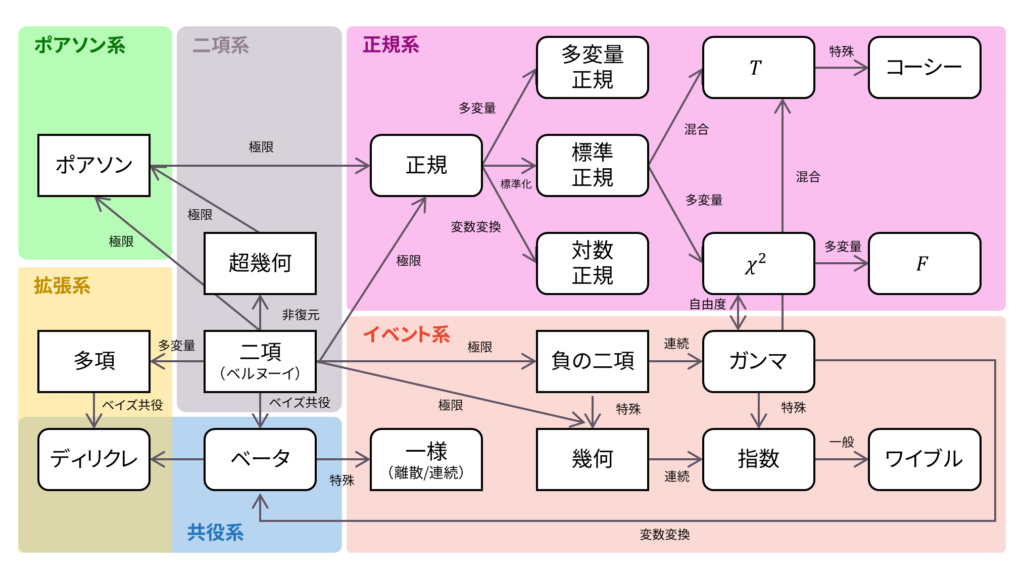
さて,ロードマップに戻りましょう。 多項分布は二項分布を多変量に拡張したものでした。本ロードマップの拡張系に分類されるのは多項分布しかありませんので,覚えやすい位置付けになっています。以下の内容も参考になるでしょう。
参考文献
本稿の執筆にあたり参考にした文献は,以下でリストアップしております。


コメント
コメント一覧 (3件)
式(20)について質問させてください。
二項分布の再生性は、成功確率pが等しい確率変数Xi~Bin(m,p), Xj~Bin(n,p)があるときにXi+Xj~Bin(m+n,p)が成り立つことと理解しており、成功確率が異なる確率変数に対しては成り立たないと理解しているのですが、式(20)のような成功確率が等しくない場合にも成立する特別な場合があるのでしょうか?
ご指摘ありがとうございます。たしかに再生性という言葉の使い方が不適切でした。内容を修正しましたので、お手数ですがご確認お願い致します。
ご対応ありがとうございます。公開いただいている質の高いコンテンツは、統計およびAWSの勉強の際にいつも参考にさせていただいています。引き続きよろしくお願いします。