はじめに
本稿では,統計検定1級の数理統計分野で必ずおさえておくべきポイントをまとめます。特に断りなく下記のノーテーションを利用します。
| 記号 | 意味 |
|---|---|
| $a,b$ | 実定数 |
| $p$ | $0\leq p\leq 1$なる確率を表す変数 |
| $q$ | $1-p$なる確率を表す変数 |
| $X_{(i)}$ | 第$i$順序統計量 |
ベースとなる基礎知識
確率関数・母関数
離散一様分布の確率関数と母関数を求めよ。
一様分布の意味を踏まえると,確率質量関数は
f(x) &=
\begin{cases}
\displaystyle
\frac{1}{n}&(x=1,2,\ldots,n)\\[0.7em]
0&(\text{その他})
\end{cases}
\end{align}
となる。$f(x)=0$のときは確率母関数も$0$になる。そこで,$x=1,2,\ldots,n$のときの確率母関数を求める。定義より,
G(s) &= E[s^{X}] = \sum_{x=1}^{n}\frac{s^{x}}{n}
\end{align}
と表される。安直に等比級数の和の公式を利用したいが,分母が$0$となる条件に注意する。ここで,確率母関数は$|s|\leq 1$で定義されることを思い出したい。$|s|<1$のときと$s=1$のときで場合分けをして,
G(s) &=
\begin{cases}
\displaystyle
\frac{s(1-s^{n})}{n(1-s)}&(|s|<1)\\[0.7em]
1&(s=1)
\end{cases}
\end{align}
と表される。
連続一様分布の確率関数と母関数を求めよ。
一様分布の意味を踏まえると,確率密度関数は
f(x) &=
\begin{cases}
\displaystyle
\frac{1}{b-a}&(a\leq x\leq b)\\[0.7em]
0&(\text{その他})
\end{cases}
\end{align}
と表される。$f(x)=0$のときはモーメント母関数も$0$になる。そこで,$a\leq x\leq b$のときのモーメント母関数を求める。定義より,
M(t) &= E[e^{tX}] = \int_{a}^{b}\frac{e^{tx}}{b-a}dx = \frac{e^{bt}-e^{at}}{(b-a)t}
\end{align}
と表される。
ベルヌーイ分布の確率関数と母関数を求めよ。
ベルヌーイ分布の意味を踏まえると,確率質量関数は
f(x) &= p^{x}q^{1-x}
\end{align}
と表される。ただし,$x\in\{0,1\}$である。定義より,確率母関数は
G(s) &= E[s^{X}] = \sum_{x=0}^{1}(ps)^{x}q^{1-x} = ps+q
\end{align}
と表される。
二項分布の確率関数と母関数を求めよ。
二項分布の意味を踏まえると,確率質量関数は
f(x) &= {}_{n}C_{x}p^{x}q^{n-x}
\end{align}
と表される。ただし,$x=1,\ldots,n$である。定義より,確率母関数は
G(s) &= E[s^{X}] = \sum_{x=0}^{\infty}{}_{n}C_{x}p^{x}(ps)^{x}q^{n-x} = (ps+q)^{n}
\end{align}
と表される。
ポアソン分布の確率関数と母関数を求めよ。
二項分布において$np=\lambda$を一定に保ちながら$n\rarr\infty$とする。以下のように理解する。
f(x) &= \frac{n!}{x!(n-x)!}p^{x}(1-p)^{n-x}\\[0.7em]
&\approx \frac{n^{x}}{x!}p^{x}(1-p)^{n}\\[0.7em]
&= \frac{\lambda^{x}}{x!}\left\{ \left(1+\frac{1}{-n/\lambda} \right)^{-n/\lambda} \right\}^{-\lambda}\\[0.7em]
&\rightarrow \frac{\lambda^{x}}{x!}e^{-\lambda}
\end{align}
ただし,$x=1,\ldots$である。定義より,確率母関数は
G(s) &= E[s^{X}]
= \sum_{x=0}^{\infty}\frac{(\lambda s)^{x}}{x!}e^{-\lambda}
= e^{\lambda(s-1)}
\end{align}
と表される。
幾何分布の確率関数と母関数を求めよ。
幾何分布は「無限に続くベルヌーイ試行において$1$回成功するまでの失敗の回数」が従う分布であるため,確率質量関数は
f(x) &= pq^{x}
\end{align}
と表される。ただし,$x=1,\ldots$である。定義より,確率母関数は
G(s) &= E[s^{X}]
= \sum_{x=0}^{\infty}p(qs)^{x}
= \frac{p}{1-qs}
\end{align}
と表される。
負の二項分布の確率関数と母関数を求めよ。
負の二項分布は「無限に続くベルヌーイ試行において$r$回成功するまでの失敗の回数」が従う分布であるため,確率質量関数は
f(x) &= {}_{r+x-1}C_{x}~p^{r}q^{x}
\end{align}
と表される。ただし,$x=1,\ldots$である。負の二項分布は幾何分布に従う$r$個の確率変数$X_{1},\ldots,X_{n}$の和であることから,確率母関数は
G(s) &= E[s^{X_{1},\ldots,X_{r}}]
= E[s^{X_{1}}]\cdots E[s^{X_{r}}]
= \left(\frac{p}{1-qs}\right)^{r}
\end{align}
と表される。
多項分布の確率関数と母関数を求めよ。
多項分布の意味を踏まえると,確率質量関数は
f(x) &= \frac{n!}{x_{1}!\cdots x_{k}!}(p_{1}s_{1})^{x_{1}}\cdots (p_{k-1}s_{k-1})^{x_{k}}p_{k}^{x_{k}}
\end{align}
と表される。多項分布は$x_{1}+\cdots+x_{k}=1$という制約条件を満たす集合$A$上で定義されるため,確率母関数の定義には$k-1$個の変数を利用すれば十分で,
G(\vs)
&= E[s_{1}^{X_{1}}\cdots s_{k-1}^{X_{k-1}}]\\[0.7em]
&= \sum_{\vx\in A}\frac{n!}{x_{1}!\cdots x_{k}!}(p_{1}s_{1})^{x_{1}}\cdots (p_{k-1}s_{k-1})^{x_{k}}p_{k}^{x_{k}}\\[0.7em]
&= (p_{1}s_{1}+\cdots+p_{k-1}s_{k-1}+p_{k})^{n}
\end{align}
と表される。
超幾何分布の確率関数と母関数を求めよ。
超幾何分布は「アタリが$M$個,ハズレが$N-M$個入っているくじ引きから$n$個を引くときのアタリの個数」が従う分布であるため,確率質量関数は
f(x) &= \frac{{}_{M} \tilde{\C}_{x} \times {}_{N-M}\tilde{\C}_{n-x}}{{}_NC_{n}}
\end{align}
と表される。ただし,二項係数${}_{M}C_{x}$および${}_{N-M}\tilde{\C}_{n-x}$はそれぞれ$x{=}0,\ldots,M$および$n{-}x{=}0,\ldots,N{-}M$で定義されるが,$f(x)$の定義域は$x\in\{0,\ldots,n\}$であるため,二項係数の定義域以外では$0$をとる二項係数を拡張したような記号$\tilde{C}$を導入した。また,超幾何分布の確率母関数は複雑な形をしており,平均と分散の導出に利用されないため割愛する。
正規分布の確率関数と母関数を求めよ。
正規分布の確率密度関数の導出は複雑であるため,暗記してしまった方が結果として楽である。
f(x) &= \frac{1}{\sqrt{2\pi\sigma^2}}\exp\left\{ -\frac{(x-\mu)^{2}}{2\sigma^2} \right\}
\end{align}
ただし,$x\in\mR$である。定義より,モーメント母関数は
M(t)
&= E[e^{tX}]\\[0.7em]
&= \int_{-\infty}^{\infty}\frac{1}{\sqrt{2\pi\sigma^2}}\exp\left\{ tx-\frac{(x-\mu)^2}{2\sigma^2} \right\}\\[0.7em]
&= \int_{-\infty}^{\infty}\frac{1}{\sqrt{2\pi\sigma^2}}\exp\left\{ \frac{x^{2}-2(\mu+\sigma^{2}t) x+\mu^{2}}{2\sigma^2} \right\}\\[0.7em]
&= \int_{-\infty}^{\infty}\frac{1}{\sqrt{2\pi\sigma^2}}\exp\left[ \frac{\{x-(\mu+\sigma^{2}t)\}^{2}+2\mu\sigma^{2}t+\sigma^{4}t^{2}}{2\sigma^2} \right]\\[0.7em]
&= \exp\left(\mu t+\frac{\sigma^{2}t^{2}}{2}\right)
\end{align}
と表される。平方完成することをおさえておく。
標準正規分布の確率関数と母関数を求めよ。
正規分布において$\mu=0$と$\sigma^{2}=1$を代入すると,標準正規分布の確率密度関数は
f(x) &= \frac{1}{\sqrt{2\pi}}\exp\left( -\frac{x^{2}}{2} \right)
\end{align}
と表される。ただし,$x\in\mR$である。同様に,モーメント母関数は
M(t) &= \exp\left(\frac{t^{2}}{2}\right)
\end{align}
と表される。
対数正規分布の確率関数と母関数を求めよ。
$X\sim\N(0,1)$に対して$Y=e^{X}$が従う分布が対数正規分布であるため,確率密度関数は
f(x)
&= \frac{1}{\sqrt{2\pi\sigma^2}}\exp\left\{ -\frac{(\log x-\mu)^{2}}{2\sigma^2} \right\}\cdot \frac{1}{x}
= \frac{1}{x\sqrt{2\pi\sigma^2}}\exp\left\{ -\frac{(\log x-\mu)^{2}}{2\sigma^2} \right\}
\end{align}
と表される。ただし,$x\in\mR_{+}$である。$Y=\log X$が従う分布ではないため注意する。逆関数が対数となる変数変換として理解する。また,簡単な計算により,モーメント母関数が発散することが確認できる。
多変量標準正規分布の確率関数と母関数を求めよ。
一次元正規分布とは異なり,導出の誘導として多変量正規分布では標準正規分布から考える。独立に標準正規分布に従う$Z_{1},\ldots,Z_{n}$に対し,同時確率密度関数$f(\vz)$は
f(\vz)
&= \prod_{i=1}^{n}\frac{1}{\sqrt{2\pi}}\exp\left( -\frac{z_{i}^{2}}{2} \right)
= \frac{1}{(2\pi)^{n/2}}\exp\left( -\frac{\vz^{T}\vz}{2} \right)
\end{align}
と表される。ただし,$x\in\mR^{n}$である。定義より,モーメント母関数は
M(\vt)
&= E[e^{\vt^{T}Z}]\\[0.7em]
&= \frac{1}{(2\pi)^{n/2}}\exp\left( -\frac{\vz^{T}\vz}{2}+\vt^{T}\vz \right)\\[0.7em]
&= \frac{1}{(2\pi)^{n/2}}\exp\left\{ -\frac{(\vz-\vt)^{T}(\vz-\vt)-\vt^{T}\vt}{2} \right\}\\[0.7em]
&= \exp\left(\frac{\vt^{T}\vt}{2}\right)
\end{align}
と表される。
多変量正規分布の確率関数と母関数を求めよ。
標準正規分布に従う$Z$に対し$X{=}AZ+\mu$が従う分布が多変量正規分布である。逆変換は$Z{=}A^{-1}(X-\mu)$であるため,確率密度関数は
f(\vx)
&= \frac{1}{(2\pi)^{n/2}}\exp\left\{ -\frac{(\vx-\vmu)^{T}(A^{-1})^{T}A^{-1}(\vx-\vmu)}{2} \right\}\abs\{\det(A^{-1})\}\\[0.7em]
&= \frac{1}{(2\pi)^{n/2}}\exp\left\{ -\frac{(\vx-\vmu)^{T}(AA^{T})^{-1}(\vx-\vmu)}{2} \right\}\abs\{\det(A)^{-1}\}\\[0.7em]
&= \frac{1}{(2\pi)^{n/2}\det(\Sigma)^{1/2}}\exp\left\{ -\frac{(\vx-\vmu)^{T}\Sigma^{-1}(\vx-\vmu)}{2} \right\}
\end{align}
と表される。ただし,$x\in\mR^{n}$であり,逆行列の行列式は行列式の逆行列となること,$X{=}AZ+\mu$で両辺の分散を考えることで$V[X]{=}AA^{T}$が導かれること,$V[X]$は$\Sigma$と表されるため$\det(\Sigma)$は$\det(A)^{2}$であることを利用した。係数部分を省略してモーメント母関数の指数部のみを平方完成すると,
&\vt^{T}\vx -\frac{1}{2}(\vx-\vmu)^T \Sigma^{-1}(\vx-\vmu)\notag\\[0.7em]
&\quad\quad= -\frac{1}{2}\left\{\vx^{T}\Sigma^{-1}\vx-2(\vmu+\Sigma\vt)^{T}\Sigma^{-1}\vx+\vmu^{T}\Sigma^{-1}\vmu\right\}\\[0.7em]
&\quad\quad= -\frac{1}{2}\left[\left\{\vx-(\vmu+\Sigma\vt)\right\}^{T}\Sigma^{-1}\left\{\vx-(\vmu+\Sigma\vt)\right\}-2\vt^{T}\vmu-\vt^{T}\Sigma^{-1}\vt\right]\\[0.7em]
&\quad\quad=\vt^{T}\vmu+\frac{1}{2}\vt^{T}\Sigma\vt-\frac{1}{2}\left(\vx-\vmu-\Sigma\vt\right)^{T}\Sigma^{-1}\left(\vx-\vmu-\Sigma\vt\right)
\end{align}
と表されるため,モーメント母関数は$\exp(\vt^{T}\vmu+\vt^{T}\Sigma\vt/2)$と表される。なお,多変量正規分布のモーメント母関数は,冪級数を用いて
M(\vt)
&=1 +\left( \vmu^T\vt + \frac{1}{2}\vt^T\Sigma\vt\right)+\left(\vt^{T}\vmu\vmu^{T}\vt\right. + \cdots\\[0.7em]
\end{align}
と表されることもある。
指数分布の確率関数と母関数を求めよ。
指数分布の導出方法のうち,幾何分布の連続拡張として導出する方法と,ポアソン分布における時間間隔として導出する方法が肝要である。
まず,幾何分布の連続拡張として導出する方法を確認する。区間$[0,\infty)$を長さ$1/n$の小区間に分割してインデックスを$k$とおくと,時刻$t$は$k/n$に離散化される。インデックス$k$まで失敗し,インデックス$k{+}1$で初めて成功するという事象は幾何分布に従うが,この幾何分布のパラメータを$p{=}\lambda/n$とおく。このように置く理由は,二項分布の極限としてポアソン分布を導出する際に利用される$np{=}\lambda$という定義と整合性を保つためである。一方,時刻$t$で初めて成功するという事象を表す確率変数が従う分布を指数分布と定義すると,微小区間$dt$で初めて成功する確率は$f(t)dt$と表される。幾何分布と指数分布の意味から,$\lambda/n$をパラメータとする幾何分布において$n\rarr\infty$を考えると指数分布になるため,
\lim_{n\rightarrow \infty} (1-p)^{k}p
&=\lim_{n\rightarrow \infty} \left(1-\frac{\lambda}{n}\right)^{k} \frac{\lambda}{n} \\[0.7em]
&=\lambda\lim_{n\rightarrow \infty} \left(1-\frac{\lambda}{n}\right)^{nt}~dt \\[0.7em]
&=\lambda\lim_{n\rightarrow \infty} \left\{ \left(1-\frac{\lambda}{n}\right)^{-n/\lambda}\right\}^{-\lambda t} dt \\[0.7em]
&\rightarrow \lambda e^{-\lambda t} dt = f(t)dt
\end{align}
と表される。したがって,指数分布の確率密度関数は$\lambda e^{-\lambda t}$である。ただし,$t\in\mR_{+}$である。
次に,ポアソン分布における時間間隔として導出する方法を確認する。ポアソン分布に従う確率変数$X$に対し,単位時間あたりに成功する回数の期待値を$\lambda$とおくと,
f(x) &= \frac{(\lambda t)^{x}}{x!}e^{-\lambda t}
\end{align}
となる。初めて成功するまでの待ち時間を$T$とおくと,時間$t$で初めて成功する確率は
p(T\leq t) &= 1-p(T > t) = 1 - f(0) = 1-e^{-\lambda t}
\end{align}
と表される。$T$が従う分布を指数分布と定義すると,$p(T\leq t)$は指数分布の累積密度関数であるため,指数分布の確率密度関数は
\frac{d}{dt} (1-e^{-\lambda t}) &= \lambda e^{-\lambda t}
\end{align}
と表される。モーメント母関数の定義より,$t$は$0$の近くで定義されることから$t-\lambda<0$としてよく,
M(t) &= \int_{0}^{\infty}\lambda e^{(t-\lambda)x}dx = \left(\frac{\lambda}{\lambda-t}\right) = \left(1-\frac{t}{\lambda}\right)^{-1}
\end{align}
と表される。
ガンマ分布の確率関数と母関数を述べよ。
ガンマ分布はポアソン分布と形が似ていること,ガンマ関数の形が現れることの二点をおさえておく。
f(x)
&= \frac{\text{パラメータ}^{n}}{\text{階乗}}\cdot\text{ガンマ関数}
= \frac{\lambda^{n}}{\Gamma(n)}x^{n-1}e^{-\lambda x}
\end{align}
ただし,ガンマ関数の定義域より$x\in\mR_{+}$である。愚直に計算で導出しようとすると多変数から一変数への変換が必要になるため,確率密度関数に関しては覚えてしまった方が楽である。確率密度関数が分かれば,モーメント母関数は
M(x)
&= \int_{0}^{\infty}\frac{\lambda^{n}}{\Gamma(n)}x^{n-1}e^{-(\lambda-t) x}dx\\[0.7em]
&= \frac{\lambda^{n}}{\Gamma(n)}\int_{0}^{\infty}\left(\frac{y}{\lambda-t}\right)^{n-1}e^{-y}\frac{dy}{\lambda-t}\\[0.7em]
&= \left(\frac{\lambda}{\lambda-t}\right)^{n}
\end{align}
と求められる。これは,ガンマ分布が指数分布に従う確率変数の和として定義されることからも導かれる。
ベータ分布の確率関数と母関数を述べよ。
二項分布の共役事前分布がベータ分布であること,ベータ分布の正規化定数がベータ関数と定義されることから,
f(x)
&= \frac{1}{B(a,b)}x^{a-1}(1-x)^{b-1}
= \frac{\Gamma(a+b)}{\Gamma(a)\Gamma(b)}x^{a-1}(1-x)^{b-1}
\end{align}
と求められる。ただし,$x\in(0,1)$である。また,ベータ関数のモーメント母関数は複雑な形をしているため割愛する。
ディリクレ分布の確率関数と母関数を述べよ。
多項分布の共役事前分布がディリクレ分布になるが,ベータ分布が二項分布の共役事前分布であることから,ディリクレ分布の確率密度関数はベータ分布を多次元に拡張すればよい。
f(x)
&= \frac{1}{B(\valpha)}\prod_{i=1}^{k}x_{i}^{\alpha_{i}-1}
= \frac{\Gamma(\alpha_{1}+\cdots\alpha_{k})}{\Gamma(\alpha_{1})\cdots\Gamma(\alpha_{k})}\prod_{i=1}^{k}x_{i}^{\alpha_{i}-1}
\end{align}
ただし,$x_{1}+\cdots+x_{k}=1$である。ベータ分布同様,モーメント母関数は複雑な形をしているため割愛する。
コーシー分布の確率関数と母関数を述べよ。
$X\sim\U(-\pi/2,\pi/2)$に対して$Y=\tan X$が従う分布がコーシー分布であることから,確率密度関数は
f(y) &= \frac{1}{\pi}\frac{1}{y^{2}+1}
\end{align}
と表される。ただし,$y\in\mR$である。コーシー分布のモーメント母関数は存在しない。
ワイブル分布の確率関数と母関数を述べよ。
危険率が$ct^{b}$となる確率分布がワイブル分布であることから,確率密度関数は
-\frac{d}{dt}\exp\left(-\int_{0}^{t}cu^{b}du\right)
&= -\frac{d}{dt}\exp\left(-\frac{ct^{b+1}}{b+1}\right)
= ct^{b}\exp\left(-\frac{ct^{b+1}}{b+1}\right)
\end{align}
と表される。ただし,$y\in\mR_{+}$である。ワイブル分布の平均と分散はモーメント母関数を使わずとも簡単に求められるため割愛する。
カイ二乗分布の確率関数と母関数を求めよ。
$X\sim\N(0,1)$に対し$Y=X^{2}$が従う分布が$\chi^{2}(1)$であることから,確率密度関数は
f(y)
&= \frac{d}{dy}P(X^{2}\leq y)\\[0.7em]
&= \frac{d}{dy}P(-\sqrt{y}\leq X\leq \sqrt{y})\\[0.7em]
&= 2\frac{d}{dy}\int_{0}^{\sqrt{y}}f(x)dx\\[0.7em]
&= y^{-1/2}f(\sqrt{y})\\[0.7em]
&= \frac{1}{2^{1/2}\sqrt{\pi}}y^{-1/2}e^{-y/2}\\[0.7em]
&= \frac{1}{2^{1/2}\Gamma(1/2)}y^{1/2-1}e^{-y/2}\\[0.7em]
&= \Ga\left(\frac{1}{2},\frac{1}{2}\right)
\end{align}
と表される。ただし,$y\in\mR_{+}$であり,標準正規分布の確率密度関数を$f$とおいた。なお,$y<0$のときは$x^{2}\leq y$を満たす$y$が存在しないため,確率密度は$0$となる。ガンマ分布の再生性から,$\chi^{2}(n)$の確率密度関数は$\Ga(n/2,1/2)$であり,
f(y) &= \frac{1}{2^{n/2}\Gamma(n/2)}y^{n/2-1}e^{-y/2}
\end{align}
と表される。定義より,モーメント関数は
M(t) &= \int_{0}^{\infty}\frac{1}{2^{n/2}\Gamma(n/2)}x^{n/2-1}e^{-(1-2t)x/2}dx\\[0.7em]
&= \int_{0}^{\infty}\frac{1}{2^{n/2}\Gamma(n/2)}\left(\frac{y}{1-2t}\right)^{n/2-1}e^{-y/2}\frac{dy}{1-2t}\\[0.7em]
&= (1-2t)^{-n/2}
\end{align}
と表される。
$F$分布の確率関数と母関数を求めよ。
$U{\sim}\chi^{2}(p)$と$V{\sim}\chi^{2}(q)$に対し$(U/p)/(V/q)$が従う分布が$F$分布である。まず$Z{=}U/V$が従う分布を求める。$\chi^{2}(n)$が$\Ga(n/2,1/2)$となること,およびガンマ分布とベータ分布の関係より,$Y{=}U/(U{+}V)$は$\Be(p/2,q/2)$に従う。一方,$Y{=}Z/(1{+}Z)$であることから,$Z$の従う確率密度関数$f$は$Y$の従う確率密度関数$g$を用いて
f(z)
&= g(y)\frac{dy}{dz}\\[0.7em]
&= \frac{1}{B(p/2,q/2)}\left(\frac{z}{1+z}\right)^{p/2-1}\left(\frac{z}{1+z}\right)^{q/2-1}\frac{1}{(1+z)^{2}}\\[0.7em]
&= \frac{1}{B(p/2,q/2)}\frac{z^{p/2-1}}{(1+z)^{(p+q)/2}}
\end{align}
と表される。ただし,$z\in\mR_{+}$である。したがって,$X{=}(q/p)Z$の確率密度関数は
f(x)
&= \frac{1}{B(p/2,q/2)}\frac{\{(p/q)x\}^{p/2-1}}{\{1+(p/q)x\}^{(p+q)/2}}(p/q)\\[0.7em]
&= \frac{p^{p/2}q^{q/2}}{B(p/2,q/2)}\frac{x^{p/2-1}}{(px+q)^{(p+q)/2}}
\end{align}
と表される。$F$分布のモーメント母関数は存在しない。
$t$分布の確率関数と母関数を求めよ。
$Z{\sim}\N(0,1)$と$W{\sim}\chi^{2}(n)$に対し,$X{=}Z/\sqrt{W/n}$が従う分布が$t(n)$である。$Y{=}W$とおくと,$Z$と$W$の逆変換は
z &= x\sqrt{\frac{y}{n}},\quad w=y
\end{align}
であり,ヤコビアンは
\det J
&= \det
\begin{pmatrix}
\partial z/\partial x&\partial z/\partial y\\
\partial w/\partial x&\partial w/\partial y
\end{pmatrix}
= \det
\begin{pmatrix}
\sqrt{y/n}&*\\
0&1
\end{pmatrix}
= \sqrt{\frac{y}{n}}
\end{align}
であるため,$X$の確率密度関数は
\int_{0}^{\infty}f(x,y)dy
&= \int_{0}^{\infty}\frac{1}{\sqrt{2\pi}}e^{x^{2}y/(2n)}\frac{y^{n/2-1}e^{-y/2}}{\Gamma(n/2)2^{n/2}}\sqrt{\frac{y}{n}}dy\\[0.7em]
&= \frac{1}{\sqrt{2\pi n}\Gamma(n/2)2^{n/2}}\int_{0}^{\infty} y^{(n+1)/2-1}e^{-y(1+x^{2}/n)/2} dy
\end{align}
と表される。ただし,$x\in\mR$である。$m{=}(1+x^{2}/n)/2$および$s{=}my$とおくと,
f(x)
&= \frac{1}{\sqrt{2\pi n}\Gamma(n/2)2^{n/2}}\int_{0}^{\infty} (sm^{-1})^{(n+1)/2-1}e^{-s} (m^{-1}ds)\\[0.7em]
&= \frac{m^{-(n+1)/2}}{\sqrt{2\pi n}\Gamma(n/2)2^{n/2}}\int_{0}^{\infty} s^{(n+1)/2-1}e^{-s} ds\\[0.7em]
&= \frac{2^{(n+1)/2}}{\sqrt{2\pi n}\Gamma(n/2)2^{n/2}}\left(1+\frac{x^{2}}{n}\right)^{-(n+1)/2}\Gamma\left(\frac{n+1}{2}\right)\\[0.7em]
&= \frac{\Gamma(n/2+1/2)}{\sqrt{n}\Gamma(n/2)\Gamma(1/2)}\left(1+\frac{x^{2}}{n}\right)^{-(n+1)/2}\\[0.7em]
&= \frac{1}{\sqrt{n}B(n/2,1/2)}\left(1+\frac{x^{2}}{n}\right)^{-(n+1)/2}
\end{align}
と表される。$t$分布のモーメント母関数は存在しない。
標準ロジスティック分布の確率関数と母関数を求めよ。
累積密度関数が標準シグモイド関数$\sigma(x)$となる分布が標準ロジスティック分布であるため,確率密度関数は
f(x) &= \frac{d}{dx}\frac{1}{1+e^{-x}} = \frac{e^{-x}}{(1+e^{-x})^{2}}
\end{align}
と表される。ただし,$x\in\mR$である。$u{=}\sigma(x)$とおくと,$e^{x}{=}u/(1-u)$および$du/dx{=}u(1-u)$となることから,モーメント母関数は
M(t)
&= \int_{0}^{\infty}\frac{e^{(t-1)x}}{(1+e^{-x})^{2}}dx\\[0.7em]
&= \int_{0}^{1}\left\{u/(1-u)\right\}^{t-1}\cdot u^{2}\frac{du}{u(1-u)}\\[0.7em]
&= \int_{0}^{1}\left\{u/(1-u)\right\}^{t}du\\[0.7em]
&= \int_{0}^{1}u^{(1+t)-1}(1-u)^{(1-t)-1}du\\[0.7em]
&= B(1+t,1-t)
= \Gamma(1+t,1-t)
\end{align}
と表される。
ゴンペルツ分布の確率関数と母関数を求めよ。
危険率が$ce^{bt}$となる分布がゴンペルツ分布であることから,確率密度関数は
-\frac{d}{dt}\exp\left(-\int_{0}^{t}ce^{bu}du\right)
&= -\frac{d}{dt}\exp\left(-\frac{ce^{bt}}{b}+\frac{c}{b}\right)
= c\exp\left(bt-\frac{c}{b}e^{bt}+\frac{c}{b}\right)
\end{align}
と表される。ただし,$x\in\mR_{+}$である。モーメント母関数は複雑な形をしているため割愛する。
ラプラス分布の確率関数と母関数を求めよ。
指数分布を$y$軸に対して対象に貼り付けた分布がラプラス分布であるため,確率密度関数は
f(x) &= C\exp\left(-\frac{|x-\mu|}{b}\right)
\end{align}
と表される。ただし,$x\in\mR$である。正規化定数$C$は
\frac{1}{C}
&= 2\int_{\mu}^{\infty}\exp\left(-\frac{x-\mu}{b}\right)
= 2\left[-b\exp\left(-\frac{x-\mu}{b}\right)\right]_{\mu}^{\infty}
= 2b
\end{align}
を満たすため,$C=1/(2b)$となる。定義より,モーメント母関数は
M(t)
&= \frac{1}{2b}\int_{-\infty}^{\infty}\exp\left(tx-\frac{|x-\mu|}{b}\right)dx\\[0.7em]
&= \frac{1}{2b}\int_{-\infty}^{\infty}\exp\left(t(by+\mu)-\frac{|y|}{b}\right)(bdy)\\[0.7em]
&= \frac{e^{\mu t}}{2}\int_{-\infty}^{\infty}e^{bty-|y|}dy\\[0.7em]
&= \frac{e^{\mu t}}{2}\left\{\int_{-\infty}^{0}e^{(1+bt)y}dy+\int_{0}^{\infty}e^{-(1-bt)y}dy\right\}\\[0.7em]
&= \frac{e^{\mu t}}{2}\left(\frac{1}{1+bt}+\frac{1}{1-bt}\right)\\[0.7em]
&= \frac{e^{\mu t}}{1-b^{2}t^{2}}
\end{align}
と表される。ただし,収束条件より$|t|<1/b$とした。
アーラン分布の確率密度関数とモーメント母関数を求めよ。
アーラン分布は$\Ga(k,k\lambda)$であるため,$x>0$,$\lambda>0$および正の整数$k$に対し,確率密度関数は
f(x) &= \frac{(k\lambda)^{k}}{(k-1)!}x^{k-1}e^{-k\lambda x}
\end{align}
と表され,モーメント母関数は
M(t) &= \left(1-\frac{t}{k\lambda}\right)^{-k}
\end{align}
と表される。
平均・分散
離散一様分布の平均と分散を求めよ。
定義に従って計算すると,原点周りの一次モーメントは
E[X] &= \sum_{x=1}^{n}\frac{x}{n} = \frac{n+1}{2}
\end{align}
と表される。同様に,原点周りの二次モーメントは
E[X^{2}] &= \sum_{x=1}^{n}\frac{x^{2}}{n} = \frac{(n+1)(2n+1)}{6}
\end{align}
と表される。したがって,分散は
V[X] &= E[X^{2}]-E[X]^{2} = \frac{(n+1)(2n+1)}{6}-\frac{(n+1)^{2}}{4} = \frac{n^{2}-1}{12}
\end{align}
と表される。
連続一様分布の平均と分散を求めよ。
定義に従って計算すると,原点周りの一次モーメントは
E[X] &= \int_{a}^{b}\frac{x}{b-a} = \frac{b+a}{2}
\end{align}
と表される。同様に,原点周りの二次モーメントは
E[X^{2}] &= \sum_{x=1}^{n}\frac{x^{2}}{n} = \frac{b^{2}+ba+a^{2}}{3}
\end{align}
と表される。したがって,分散は
V[X] &= E[X^{2}]-E[X]^{2} = \frac{b^{2}+ba+a^{2}}{3}-\frac{(b+a)^{2}}{4} = \frac{(b-a)^{2}}{12}
\end{align}
と表される。
ベルヌーイ分布の平均と分散を求めよ。
確率母関数の性質より,原点周りの一次モーメントは
E[X] &= G^{\prime}(1) = p
\end{align}
と表される。同様に,原点周りの二次モーメントは
E[X^{2}] &= E[X(X-1)]+E[X] = G^{\prime\prime}(1)+G^{\prime}(1) = p
\end{align}
と表される。したがって,分散は
V[X] &= E[X^{2}]-E[X]^{2} = p-p^{2} = pq
\end{align}
と表される。
二項分布の平均と分散を求めよ。
確率母関数の性質より,原点周りの一次モーメントは
E[X] &= G^{\prime}(1) = np(ps+q)^{n-1}\biggr|_{s=1} = np
\end{align}
と表される。同様に,原点周りの二次モーメントは
E[X^{2}] &= E[X(X-1)]+E[X] = G^{\prime\prime}(1)+G^{\prime}(1) = n(n-1)p^{2}+np
\end{align}
と表される。したがって,分散は
V[X] &= E[X^{2}]-E[X]^{2} = n(n-1)p^{2}+np-n^{2}p^{2} = np(np-p+1-np) = npq
\end{align}
と表される。
ポアソン分布の平均と分散を求めよ。
確率母関数の性質より,原点周りの一次モーメントは
E[X] &= G^{\prime}(1) = \lambda e^{\lambda(s-1)}\biggr|_{s=1} = \lambda
\end{align}
と表される。同様に,原点周りの二次モーメントは
E[X^{2}] &= E[X(X-1)]+E[X] = G^{\prime\prime}(1)+G^{\prime}(1) = \lambda^{2}+\lambda
\end{align}
と表される。したがって,分散は
V[X] &= E[X^{2}]-E[X]^{2} = \lambda^{2}+\lambda-\lambda^{2} = \lambda
\end{align}
と表される。
超幾何分布の平均と分散を求めよ。
$i{=}1,\ldots,n$の有限母集団から抽出した標本$X_{i}$の期待値$E[X_{i}]$と分散は$V[X_{i}]$それぞれ$\mu$と$\sigma^{2}$と定義される。一方,各標本の無作為抽出は$p{=}M/N$のベルヌーイ分布に従うため,$E[X_{i}]{=}p$および$V[X_{i}]{=}pq$となる。ゆえに,$\mu{=}p$および$\sigma^{2}{=}pq$となる。
いま,有限母集団から抽出した標本の和が従う分布が超幾何分布であること,および有限母集団から抽出された観測値の標本平均の期待値は母平均と変わらず,分散は無限母集団の場合の結果に対して有限修正項を付け加えた結果となることを利用すれば,
E[X] &= nE[\oX] = n\mu = np
\end{align}
となり,
V[X] &= n^{2}V[\oX] = n^{2}\frac{N-n}{N-1}\frac{\sigma^{2}}{n} = \frac{N-n}{N-1}npq
\end{align}
となる。
幾何分布の平均と分散を求めよ。
確率母関数の性質より,原点周りの一次モーメントは
E[X] &= G^{\prime}(1) = \frac{pq}{(1-qs)^{2}}\biggr|_{s=1} = \frac{q}{p}
\end{align}
と表される。同様に,原点周りの二次モーメントは
E[X^{2}] &= E[X(X-1)]+E[X] = G^{\prime\prime}(1)+G^{\prime}(1) = \frac{2q^{2}}{p^{2}}+\frac{q}{p}
\end{align}
と表される。したがって,分散は
V[X] &= E[X^{2}]-E[X]^{2} = \frac{2q^{2}}{p^{2}}+\frac{q}{p}-\frac{q^{2}}{p^{2}} = \frac{q(q+p)}{p^{2}} = \frac{q}{p^{2}}
\end{align}
と表される。
負の二項分布の平均と分散を求めよ。
幾何分布に独立に従う$r$個の確率変数$X_{1},\ldots,X_{r}$の和が従う分布が負の二項分布であることから,
E[X_{1}+\cdots+X_{r}] &= \frac{rq}{p},\quad V[X_{1}+\cdots+X_{r}] = \frac{rq}{p^{2}}
\end{align}
と表される。
多項分布の平均と分散を求めよ。
多項分布において,ある変数$X_{i}$に関する周辺分布は$\Bin(n,p_{i})$となることから,
E[X_{i}] &= np_{i},\quad V[X_{i}] = np_{i}q_{i}
\end{align}
と表される。
正規分布の平均と分散を求めよ。
モーメント母関数の性質より,原点周りの一次モーメントは
E[X] &= M^{\prime}(0) = (\mu+\sigma^{2} t)\exp\left(\mu t+\frac{\sigma^{2}}{2}t\right)\biggr|_{t=0} = \mu
\end{align}
と表される。同様に,原点周りの二次モーメントは
E[X^{2}] &= M^{\prime\prime}(0) = \left\{(\mu+\sigma^{2} t)^{2}+\sigma^{2}\right\}\exp\left(\mu t+\frac{\sigma^{2}}{2}t\right)\biggr|_{t=0} = \mu^{2}+\sigma^{2}
\end{align}
と表される。したがって,分散は
V[X] &= E[X^{2}]-E[X]^{2} = (\mu^{2}+\sigma^{2}) - \mu^{2} = \sigma^{2}
\end{align}
と表される。
標準正規分布の平均と分散を求めよ。
定義より,$E[X]=1$および$V[X]=\sigma^{2}$となる。
対数正規分布の平均と分散を求めよ。
対数正規分布の$t$次モーメントが正規分布のモーメント母関数$M(t)$に相当するため,原点周りの一次モーメントは
E[X] &= M(1) = \exp\left(\mu+\frac{\sigma^{2}}{2}\right)
\end{align}
と表される。同様に,原点周りの二次モーメントは
E[X^{2}] &= M(2) = \exp\left(2\mu+2\sigma^{2}\right)
\end{align}
と表される。したがって,分散は
V[X] &= E[X^{2}]-E[X]^{2} = e^{2\mu+2\sigma^{2}}-e^{2\mu+\sigma^{2}} = e^{2\mu+\sigma^{2}}(e^{\sigma^{2}}-1)
\end{align}
と表される。
多変量正規分布の平均と分散を求めよ。
モーメント母関数の性質より,原点周りの一次モーメントは
E[X] &= M^{\prime}(\vzero) = \vmu + \Sigma\vt+\vmu\vmu^{T}\vt + \cdots\biggr|_{\vt=\vzero}
= \vmu
\end{align}
と表される。同様に,原点周りの二次モーメントは
E[XX^{T}] &= M^{\prime\prime}(\vzero) = \Sigma+\vmu\vmu^{T} + \cdots\biggr|_{\vt=\vzero}
= \Sigma+\vmu^{T}\vmu
\end{align}
と表される。したがって,分散は
V[X] &= E[XX^{T}]-E[X]E[X]^{T} = (\Sigma+\vmu\vmu^{T})-\vmu\vmu^{T} = \Sigma
\end{align}
と表される。
指数分布の平均と分散を求めよ。
モーメント母関数の性質より,原点周りの一次モーメントは
E[X] &= M^{\prime}(0) = \frac{1}{\lambda}\left(1-\frac{t}{\lambda}\right)^{-2}\biggr|_{t=0} = \frac{1}{\lambda}
\end{align}
と表される。同様に,原点周りの二次モーメントは
E[X^{2}] &= M^{\prime\prime}(0) = \frac{2}{\lambda^{2}}\left(1-\frac{t}{\lambda}\right)^{-3}\biggr|_{t=0} = \frac{2}{\lambda^{2}}
\end{align}
と表される。したがって,分散は
V[X] &= E[X^{2}]-E[X]^{2} = \frac{2}{\lambda^{2}}-\frac{1}{\lambda^{2}}=\frac{1}{\lambda^{2}}
\end{align}
と表される。
ガンマ分布の平均と分散を求めよ。
指数分布に独立に従う$n$個の確率変数$X_{1},\ldots,X_{n}$の和が従う分布がガンマ分布であることから,
E[X_{1}+\cdots+X_{n}] &= \frac{n}{\lambda},\quad V[X_{1}+\cdots+X_{r}] = \frac{n}{\lambda^{2}}
\end{align}
と表される。
ベータ分布の平均と分散を求めよ。
定義に従って計算すると,原点周りの一次モーメントは
E[X] &= \frac{1}{B(a,b)}\int_{0}^{1}x^{a}(1-x)^{b-1}
= \frac{\Gamma(a+b)}{\Gamma(a)\Gamma(b)}\frac{\Gamma(a+1)\Gamma(b)}{\Gamma(a+b+1)}
= \frac{a}{a+b}
\end{align}
と表される。同様に,原点周りの二次モーメントは
E[X^{2}] &{=} \frac{1}{B(a,b)}\int_{0}^{1}x^{a{+}1}(1{-}x)^{b{-}1}
{=} \frac{\Gamma(a{+}b)}{\Gamma(a)\Gamma(b)}\frac{\Gamma(a{+}2)\Gamma(b)}{\Gamma(a{+}b{+}2)}
{=} \frac{(a{+}1)a}{(a{+}b{+}1)(a{+}b)}
\end{align}
と表される。したがって,分散は
V[X] &= E[X^{2}]-E[X]^{2} = \frac{(a+1)a}{(a+b+1)(a+b)}-\frac{a^{2}}{(a+b)^{2}} = \frac{ab}{(a+b)^{2}(a+b+1)}
\end{align}
と表される。
ディリクレ分布の平均と分散を求めよ。
定義に従って計算すると,原点周りの一次モーメントは
E[X_{i}] &= \frac{\Gamma(x_{1})\cdots\Gamma(x_{i}+1)\cdots+\Gamma(x_{k})}{\Gamma(x_{1}+\cdots+x_{i}+1+\cdots+x_{k})}
= \frac{x_{i}}{x_{1}+\cdots+x_{k}}
\end{align}
と表される。同様に,原点周りの二次モーメントは
E[X_{i}^{2}] &= \frac{\Gamma(x_{1})\cdots\Gamma(x_{i}+2)\cdots+\Gamma(x_{k})}{\Gamma(x_{1}+\cdots+x_{i}+2+\cdots+x_{k})}
= \frac{(x_{i}+1)x_{i}}{(x_{1}+\cdots+x_{k}+1)(x_{1}+\cdots+x_{k})}
\end{align}
と表される。したがって,分散は
V[X] {=} E[X^{2}]{-}E[X]^{2} &{=} \frac{(x_{i}+1)x_{i}}{(x_{1}+\cdots+x_{k}+1)(x_{1}+\cdots+x_{k})}{-}\frac{x_{i}^{2}}{(x_{1}+\cdots+x_{k})^{2}}\\[0.7em]
&= \frac{(x_{i}+1)x_{i}(\sum_{j=1}^{k}x_{j})-x_{i}^{2}(\sum_{j=1}^{k}x_{j}+1)}{(\sum_{j=1}^{k}x_{j}+1)(\sum_{j=1}^{k}x_{j})^{2}}\\[0.7em]
&= \frac{x_{i}\left\{(x_{i}+1)(\sum_{j=1}^{k}x_{j}+1){-}(x_{i}+1){-}x_{i}(\sum_{j=1}^{k}x_{j}+1)\right\}}{(\sum_{j=1}^{k}x_{j}+1)(\sum_{j=1}^{k}x_{j})^{2}}\\[0.7em]
&= \frac{x_{i}\left\{(\sum_{j=1}^{k}x_{j}+1)-(x_{i}+1)\right\}}{(\sum_{j=1}^{k}x_{j}+1)(\sum_{j=1}^{k}x_{j})^{2}}\\[0.7em]
&= \frac{x_{i}(\sum_{j=1}^{k}x_{j}-x_{i})}{(\sum_{j=1}^{k}x_{j}+1)(\sum_{j=1}^{k}x_{j})^{2}}
\end{align}
と表される。
コーシー分布の平均と分散を求めよ。
コーシー分布のモーメント母関数は定義されないため,平均と分散も定義されない。
ワイブル分布の平均と分散を求めよ。
$Y=X^{b+1}/(b+1)=\kappa X^{1/\kappa}$が$\Exp(c)$に従うときに$X$が従う分布がワイブル分布であるため,原点周りの一次モーメントは
E[X] &= E[(\kappa^{-1}Y)^{\kappa}]\\[0.7em]
&= \kappa^{-\kappa}E[Y^{\kappa}]\\[0.7em]
&= \kappa^{-\kappa}\int_{0}^{\infty}y^{\kappa}ce^{-cy}dy\\[0.7em]
&= c\kappa^{-\kappa}\int_{0}^{\infty}y^{(\kappa+1)-1}e^{-cy}dy\\[0.7em]
&= c\kappa^{-\kappa}\frac{\Gamma(\kappa+1)}{c^{\kappa+1}}\\[0.7em]
&= \frac{\kappa^{-\kappa}\Gamma(\kappa+1)}{c^{\kappa}}
\end{align}
と表される。同様に,原点周りの二次モーメントは
E[X^{2}] &= \frac{\kappa^{-2\kappa}\Gamma(2\kappa+1)}{c^{2\kappa}}
\end{align}
と表される。したがって,分散は
V[X] = E[X^{2}]{-}E[X]^{2} &= \frac{\kappa^{-2\kappa}\Gamma(2\kappa+1)}{c^{2\kappa}}-\frac{\kappa^{-2\kappa}\Gamma^{2}(\kappa+1)}{c^{2\kappa}}\\[0.7em]
&= (c\kappa)^{-2\kappa}\left\{\Gamma(2\kappa+1)-\Gamma^{2}(\kappa+1)\right\}
\end{align}
と表される。
カイ二乗分布の平均と分散を求めよ。
モーメント母関数の性質より,原点周りの一次モーメントは
E[X] &= M^{\prime}(0) = n(1-2t)^{-n/2-1}\biggr|_{t=0} = n
\end{align}
と表される。同様に,原点周りの二次モーメントは
E[X^{2}] &= M^{\prime\prime}(0) = n(n+2)(1-2t)^{-n/2-2}\biggr|_{t=0} = n(n+2)
\end{align}
と表される。したがって,分散は
V[X] &= E[X^{2}]-E[X]^{2} = n(n+2) - n^{2} = 2n
\end{align}
と表される。
$F$分布の平均と分散を求めよ。
$U{\sim}\chi^{2}(p)$と$V{\sim}\chi^{2}(q)$に対し$Y{=}U/(U+V)$は$\Be(p/2,q/2)$に従い,$X{=}(q/p)U/V$を$Y$を用いて表すと$X{=}(q/p)Y/(1-Y)$となることに注意すると,原点周りの一次モーメントは
E[X]
&= \frac{q}{p}E\left[\frac{Y}{1-Y}\right]\\[0.7em]
&= \frac{q}{p}\int_{0}^{1}\frac{y^{(p/2+1)-1}(1-y)^{(q/2-1)-1}}{B(p/2,q/2)}dy\\[0.7em]
&= \frac{q}{p}\frac{B(p/2+1,q/2-1)}{B(p/2,q/2)}\\[0.7em]
&= \frac{q}{p}\frac{\Gamma(p/2+1)\Gamma(q/2-1)}{\Gamma(p/2)\Gamma(q/2)}\\[0.7em]
&= \frac{q}{p}\frac{p/2}{q/2-1}\\[0.7em]
&= \frac{q}{q-2}
\end{align}
と表される。ただし,ガンマ関数の定義域より$q>2$とする。同様に,原点周りの二次モーメントは
E[X^{2}]
&= \frac{q^{2}}{p^{2}}E\left[\frac{Y^{2}}{(1-Y)^{2}}\right]\\[0.7em]
&= \frac{q^{2}}{p^{2}}\int_{0}^{1}\frac{y^{(p/2+1)-2}(1-y)^{(q/2-1)-2}}{B(p/2,q/2)}dy\\[0.7em]
&= \frac{q^{2}}{p^{2}}\frac{B(p/2+2,q/2-2)}{B(p/2,q/2)}\\[0.7em]
&= \frac{q^{2}}{p^{2}}\frac{\Gamma(p/2+2)\Gamma(q/2-2)}{\Gamma(p/2)\Gamma(q/2)}\\[0.7em]
&= \frac{q^{2}}{p^{2}}\frac{(p/2+1)p/2}{(q/2-2)(q/2-1)}\\[0.7em]
&= \frac{q^{2}(p+2)}{p(q-2)(q-4)}
\end{align}
と表される。ただし,ガンマ関数の定義域より$q>4$とする。したがって,分散は
V[X] &= E[X^{2}]-E[X]^{2} = \frac{q^{2}(p+2)}{p(q-2)(q-4)}-\frac{q^{2}}{(q-2)^{2}}
= 2\left(\frac{q}{q-2}\right)^{2}\frac{p+q-2}{p(q-4)}
\end{align}
と表される。
$t$分布の平均と分散を求めよ。
定義に従って計算すると,原点周りの一次モーメントは
E[X]
&= \int_{-\infty}^{\infty}\frac{x}{\sqrt{n}B(n/2,1/2)}\left(1+\frac{x^{2}}{n}\right)^{-(n+1)/2}dx
\end{align}
と式変形される。被積分関数は奇関数であることから,被積分関数が収束するならば$E[X]$は$0$となる。被積分関数を展開すると,
E[X]
&= \int_{-\infty}^{\infty}\frac{x}{\sqrt{n}B(n/2,1/2)}\left(1+\frac{x^{2}}{n}\right)^{-(n+1)/2}dx\\[0.7em]
&= \frac{1}{\sqrt{n}B(n/2,1/2)}\int_{-\infty}^{\infty}x\left(1+\frac{x^{2}}{n}\right)^{-(n+1)/2}dx\\[0.7em]
&= -\frac{\sqrt{n}}{(n+1)B(n/2,1/2)}\lim_{a\rarr\infty}\left[\left(1+\frac{x^{2}}{n}\right)^{-(n+1)/2}\right]_{-a}^{a}
\end{align}
と表される。$(a+x^{2}/n)$の指数部に注目すると,$n>1$のとき$E[X]$は存在して$0$となる。次に,t分布とベータ分布の関係性より,$U{=}(1{+}X^{2}/n)^{-1}$とおくと$U{\sim}\Be(n/2,1/2)$となることを利用すると,原点周りの二次モーメントは
E[X^{2}]
&= E[nU^{-1}-n]\\[0.7em]
&= nE[U^{-1}]-n\\[0.7em]
&= n\int_{0}^{1}\frac{u^{(n/2-1)-1}(1-u)^{1/2-1}}{B(n/2,1/2)}-n\\[0.7em]
&= n\frac{B(n/2-1,1/2)}{B(n/2,1/2)}-n\\[0.7em]
&= n\frac{\Gamma(n/2-1)\Gamma(1/2)\Gamma(n/2+1/2)}{\Gamma(n/2-1/2)\Gamma(n/2)\Gamma(1/2)}-n\\[0.7em]
&= n\frac{n/2-1/2}{n/2-1}-n\\[0.7em]
&= \frac{n}{n-2}
\end{align}
と表される。ただし,ガンマ関数の定義域より$n>2$とする。したがって,分散は
V[X] &= E[X^{2}]-E[X]^{2} = \frac{n}{n-2}
\end{align}
と表される。
ロジスティック分布の平均と分散を求めよ。ただし,$\psi^{(1)}(1)=\pi^{2}/6$を利用してもよい。
モーメント母関数の性質より,原点周りの一次モーメントは
E[X] &= M^{\prime}(0) = \Gamma^{\prime}(1)\Gamma(1)-\Gamma(1)\Gamma^{\prime}(1) = 0
\end{align}
と表される。同様に,原点周りの二次モーメントは
E[X^{2}] &= M^{\prime\prime}(0) = 2\left(\Gamma^{\prime\prime}(1)-\Gamma^{\prime}(1)\Gamma^{\prime}(1)\right)\label{ロジスティック分布_二次モーメント}
\end{align}
と表される。式($\ref{ロジスティック分布_二次モーメント}$)の右辺は対数ガンマ関数の導関数であるディガンマ関数$\psi(x)$を用いて求めることができる。ポリガンマ関数$\psi^{(m)}(x)$はディガンマ関数の$m$階微分として定義され,$m=1$のとき
\psi^{(1)}(1)
&{=} \frac{d}{dx}\left(\frac{d}{dx}\log \Gamma(x)\right)\Biggr|_{x=1}
{=} \frac{\Gamma^{\prime\prime}(x)\Gamma(x){-}\Gamma^{\prime}(x)\Gamma^{\prime}(x)}{\Gamma^{2}(x)}\Biggr|_{x=1}
{=} \Gamma^{\prime\prime}(1){-}\Gamma^{\prime}(1)\Gamma^{\prime}(1)
\end{align}
となる。$\psi^{(1)}(1)=\pi^{2}/6$が与えられていることから,分散は
V[X] &= E[X^{2}]-E[X]^{2} = 2\left(\Gamma^{\prime\prime}(1)-\Gamma^{\prime}(1)\Gamma^{\prime}(1)\right) = \frac{\pi^{2}}{3}
\end{align}
と表される。
ゴンペルツ分布の平均と分散を求めよ。
ゴンペルツ分布の平均と分散は複雑な形をしているため割愛する。
ラプラス分布の平均と分散を求めよ。
モーメント母関数の性質より,原点周りの一次モーメントは
E[X]
&= M^{\prime}(0)
= \left(\mu M(t)+\frac{2b^{2}t}{1-b^{2}t^{2}}M(t)\right)\Biggr|_{t=0}
= \mu
\end{align}
と表される。ただし,$M(0)=1$に注意する。同様に,原点周りの二次モーメントは
E[X^{2}]
{=} \left(\mu M^{\prime}(t){+}\frac{2b^{2}(1{-}b^{2}t^{2}){+}4b^{4}t^{2}}{(1{-}b^{2}t^{2})^{2}}M(t){+}\frac{2b^{2}t}{1{-}b^{2}t^{2}}M^{\prime}(t)\right)\Biggr|_{t=0}
{=}\mu^{2}{+}2b^{2}
\end{align}
と表される。したがって,分散は
V[X] &= E[X^{2}]-E[X]^{2} = \mu^{2}+2b^{2}-\mu^{2} = 2b^{2}
\end{align}
と表される。
アーラン分布の平均と分散を求めよ。
アーラン分布は$\Ga(k,k\lambda)$であるため,平均と分散は
E[X] &= \frac{k}{k\lambda} = \frac{1}{\lambda},\quad V[X] = \frac{k}{k^{2}\lambda^{2}} = \frac{1}{k\lambda^{2}}
\end{align}
となる。
重要問題
累積密度関数・変数変換・順序統計量
$k{=}1,{\ldots}$で$k{\leq}x{<}k{+}1$に対し$F(x){=}1{-}1/2^{k}$のとき,$X$の確率分布を求めよ。
離散型確率分布であることに注意すると,
P(X=k) &= F(k)-\lim_{x\rarr k-0}F(x)
= \left(1-\frac{1}{2^{k}}\right)-\left(1-\frac{1}{2^{k-1}}\right)
= \frac{1}{2^{k}}
\end{align}
が得られる。
$0{<}x{<}1,0{<}y{<}1,x{+}y<1$で$f(x,y){=}Kxy(1{-}x{-}y)$のとき,$K,f(x),f(y)$を求めよ。
$(x,y)$の積分領域を$D$とおくと,
\int\int_{D}f(x,y)dxdy
&= \int_{0}^{1}\int_{0}^{1-x}Kxy(1-x-y)dydx\\[0.7em]
&= K\int_{0}^{1}\int_{0}^{1-x}-xy^{2}+x(1-x)ydydx\\[0.7em]
&= K\left[-\frac{xy^{3}}{3}+\frac{x(1-x)y^{2}}{2}\right]_{0}^{1-x}\\[0.7em]
&= \frac{K}{6}\int_{0}^{1}x(1-x)^{3}dx\\[0.7em]
&= \frac{K}{6}\left\{\left[-\frac{1}{4}x(1-x)^{4}\right]_{0}^{1}+\frac{1}{4}\int_{0}^{1}(1-x)^{4}dx\right\}\\[0.7em]
&= \frac{K}{120}\left[(1-x)^{5}\right]_{0}^{1}
= \frac{K}{120} = 1
\end{align}
となるため,$K=120$が得られる。$x$の周辺分布は,上の計算結果より$0<x<1$のとき
f(x)
&= \int_{0}^{1-x}f(x,y)dy
= K\frac{x(1-x)^{3}}{6}
= 20x(1-x)^{3}
\end{align}
となる。対称性より,$y$の周辺分布は$0<y<1$のとき$f(y)=20y(1-y)^{3}$となる。
$Y=aX+b$の確率関数を$X$の確率関数$f$を用いて表せ。
変数変換とヤコビアンの関係より,
g(y) &= \frac{1}{|a|}f\left(\frac{y-b}{a}\right)\label{ヤコビアンを用いた変数変換}
\end{align}
となる。ヤコビアンを用いない場合は,累積密度関数を利用する。$a>0$のとき,
g(y)
&{=} G^{\prime}(y)
{=} \frac{d}{dy}P(ax{+}b\leq y)
{=} \frac{d}{dy}P\left(x\leq\frac{y-b}{a}\right)
{=} F^{\prime}\left(\frac{y-b}{a}\right)
{=} \frac{1}{a}f\left(\frac{y-b}{a}\right)
\end{align}
となり,$a<0$のとき,同様に
g(y)
{=} \frac{d}{dy}P\left(x{\geq}\frac{y{-}b}{a}\right)
{=} \frac{d}{dy}\left\{1{-}F\left(x{\leq}\frac{y{-}b}{a}\right)\right\}
{=} {-}F^{\prime}\left(\frac{y{-}b}{a}\right)
{=} {-}\frac{1}{a}f\left(\frac{y{-}b}{a}\right)
\end{align}
となる。これらを組み合わせることにより式($\ref{ヤコビアンを用いた変数変換}$)が得られる。つまり,$a$を掛け合わせる際に不等式が反転し,結果として累積分布の余事象を考えることが絶対値表記に繋がっているのである。
$X\sim\U(-1,1)$に対し,$Y=|X|$の確率密度関数を求めよ。
$Y=|X|$は非連続関数であるため,$0<y<1$に対して累積密度関数を用いて
f(y) &= F^{\prime}(Y) = \frac{d}{dy}P(|X|\leq y) = \frac{d}{dy}\int_{-y}^{y}\frac{1}{2}dx = \frac{d}{dy}y = 1
\end{align}
と求められる。
$X$が連続な累積分布関数$F$をもつとき,$Y=F(X)$の確率密度関数を求めよ。
$F$が連続で狭義単調増加関数であることから$F^{-1}$が存在し,
g(y) &= G^{\prime}(y) = \frac{d}{dy}P(Y\leq y) = \frac{d}{dy}P(X\leq F^{-1}(y)) = \frac{d}{dy}F(F^{-1}(y)) = 1
\end{align}
と求めることができる。
$X+Y$,$X-Y$,$XY$,$Y/X$の確率密度関数を求める方法を述べよ。
下表の通り,同時確率密度関数から周辺確率密度関数を求める。
| $U$ | 逆関数 | $J$の第一行 | $J$の第二行 | $J$ | $f(u)$ |
|---|---|---|---|---|---|
| $X{+}Y$ | $X{=}V,Y{=}U{-}V$ | $(0,1)$ | $(1,-1)$ | $1$ | $\int_{-\infty}^{\infty}f(x,u{-}x)dx$ |
| $X{-}Y$ | $X{=}V,Y{=}U{+}V$ | $(0,1)$ | $(1,1)$ | $1$ | $\int_{-\infty}^{\infty}f(x,x{-}u)dx$ |
| $XY$ | $X{=}V,Y{=}U/V$ | $(0,1)$ | $(1/x,*)$ | $1/|x|$ | $\int_{-\infty}^{\infty}f(x,u/x)/|x|dx$ |
| $Y/X$ | $X{=}V,Y{=}U/V$ | $(0,1)$ | $(x,*)$ | $|x|$ | $\int_{-\infty}^{\infty}f(u,ux)|x|dx$ |
$V=X$とおくと,ヤコビ行列において第一行が$(0,1)$となり$\partial y/\partial u$のみが残るため,$y=\cdots$と変形してから$u$で微分した絶対値がヤコビアンとなることに注意する。$V=X$とおく理由は,$f(u)$の形で表すときにヤコビアンを$x$を用いて表すためである。$Y/X$に関しては$X/Y$と与えられることもあるが,その場合は$x$と$y$を入れ替えた結果となるため注意する。
$x>0,y>0$に対して$f_{1}(x)=xe^{-x},f_{2}(y)=e^{-y}$のとき,$X+Y$の確率密度関数を求めよ。
$U{=}X{+}Y,V{=}X$の変数変換を用いる。逆変換は$X{=}V,Y{=}U{-}V$であり,$y{>}0$より$0{<}X{<}U$となるため,
f(u) &= \int_{0}^{u}f_{1}(x)f_{2}(u-x)dx = \int_{0}^{u}xe^{-u}dx = \frac{u^{2}e^{-u}}{2}
\end{align}
と表される。ただし,$u>0$である。
$X_{1},X_{2}$が独立に$\U(-1,1)$に従うとき,$S=X_{1}+X_{2}$の確率密度関数を求めよ。
$X,S$の確率密度関数をそれぞれ$f,g$とおくと,確率変数の四則と確率密度関数の関係より$g$の被積分関数は$f(x)f(s-x)$となる。$f$の定義域より,$x$の取り得る値の範囲は第一項目について$D_{1}=(-1,1)$であり,第二項目について$D_{2}=(s-1,s+1)$である。$x$の積分範囲は$D_{1}$と$D_{2}$の共通部分である。
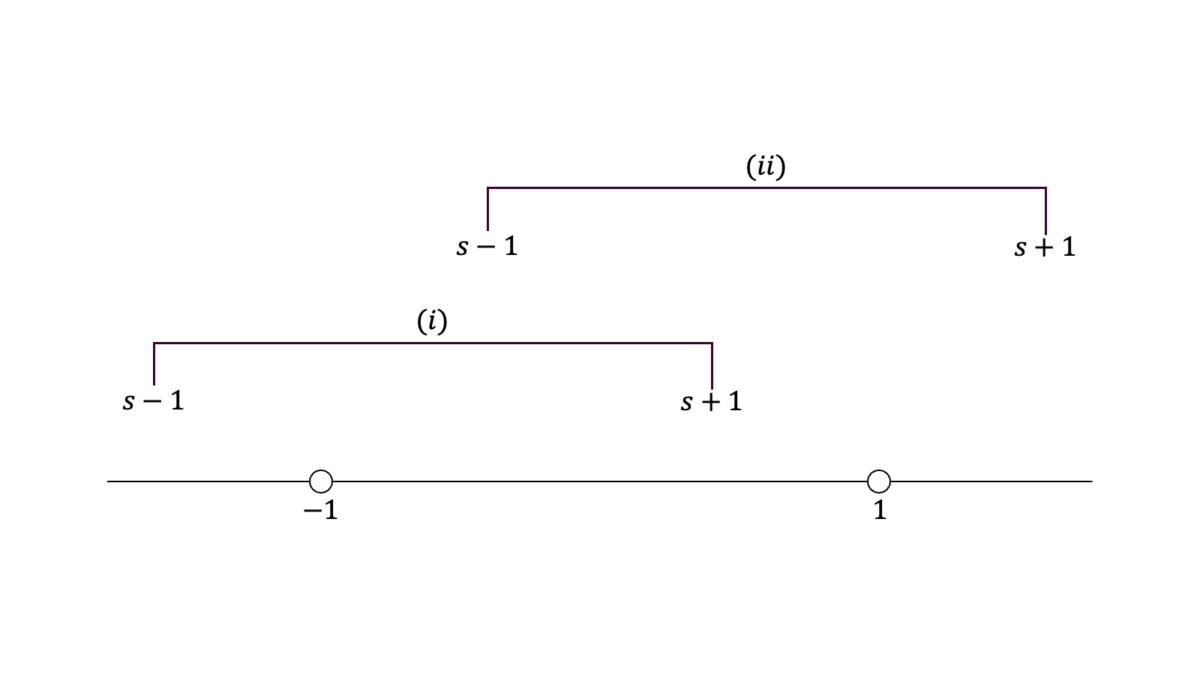
$D_{2}$の上限が$D_{1}$に含まれているとき,すなわち$-2<s<0$のとき,
g(s) &= \int_{-1}^{s+1}f(x)f(s-x)dx = \int_{-1}^{s+1}\frac{1}{4}dx = \frac{2+s}{4}
\end{align}
となる。$D_{2}$の下限が$D_{1}$に含まれているとき,すなわち$0<s<2$のとき,
g(s) &= \int_{s-1}^{1}f(x)f(s-x)dx = \int_{s-1}^{1}\frac{1}{4}dx = \frac{2-s}{4}
\end{align}
となる。それ以外の場合は$g(y)=0$となる。
$X_{1},X_{2},X_{3}$が独立に$\U(-1,1)$に従うとき,$T=X_{1}+X_{2}+X_{3}$の確率密度関数を求めよ。
前問を利用する。$X,T,S$の確率密度関数をそれぞれ$f,g,h$とおくと,確率変数の四則と確率密度関数の関係より$h$の被積分関数は被積分関数は$g(s)f(t-s)$となる。$f,g$の定義域より$s$の取り得る値の範囲は第一項目について$D_{1}{=}(-2,2)$であり,第二項目について$D_{2}{=}(t-1,t+1)$である。$s$の積分範囲は$D_{1}$と$D_{2}$の共通部分である。$g$は$s=0$を境に確率密度関数が変わること,および$D_{2}$の幅が$2$であることに注意すると,下図のような場合分けを行えばよいことが分かる。
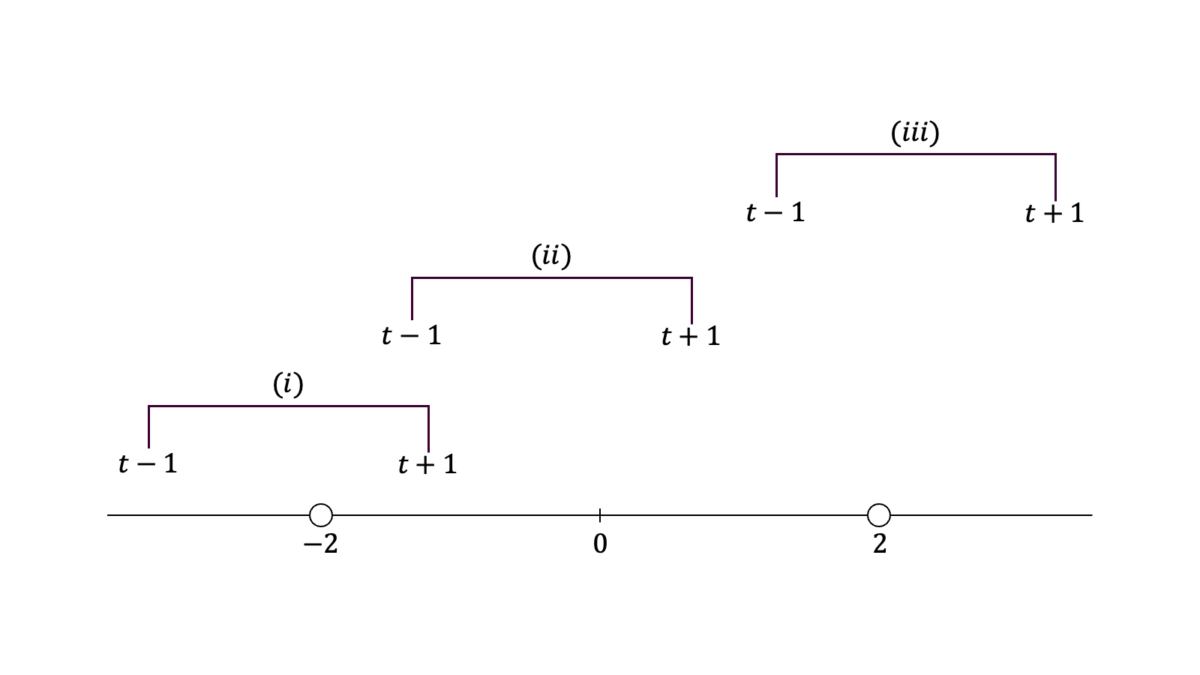
$D_{2}$の上限が$(-2,0)$に含まれているとき,すなわち$-3<t<-1$のとき,
h(t) &= \int_{-2}^{t+1}g(s)g(t-s)ds = \int_{-2}^{t+1}\frac{2+s}{8}ds =\frac{(3+t)^{2}}{16}
\end{align}
となる。$D_{2}$の下限が$(-2,0)$に,$D_{2}$の上限が$(0,2)$に含まれているとき,すなわち$-1<t<1$のとき,
h(t)
&= \int_{t-1}^{0}g(s)g(t-s)ds+\int_{0}^{t+1}g(s)g(t-s)ds\\[0.7em]
&= \int_{t-1}^{0}\frac{2+s}{8}ds+\int_{0}^{t+1}\frac{2-s}{8}ds
= \frac{3-t^{2}}{8}
\end{align}
となる。$D_{2}$の下限が$(0,2)$に含まれているとき,すなわち$1<t<3$のとき,
h(t) &= \int_{0}^{t+1}g(s)g(t-s)ds = \int_{0}^{t+1}\frac{2-s}{8}ds =\frac{(3-t)^{2}}{16}
\end{align}
となる。それ以外の場合は$h(t)=0$となる。
$X,Y$が独立に$\U(0,1)$および$\U(0,2)$に従うとき,$U=X+Y$の確率密度関数を求めよ。
$X,Y,U$の確率密度関数をそれぞれ$f,g,h$とおくと,確率変数の四則と確率密度関数の関係より$h$の被積分関数は$f(x)g(u-x)$となる。$f,g$の定義域より,$x$の取り得る値の範囲は第一項目について$D_{1}{=}(0,1)$であり,第二項目について$D_{2}{=}(u-2,u)$である。$x$の積分範囲は$D_{1}$と$D_{2}$の共通部分である。
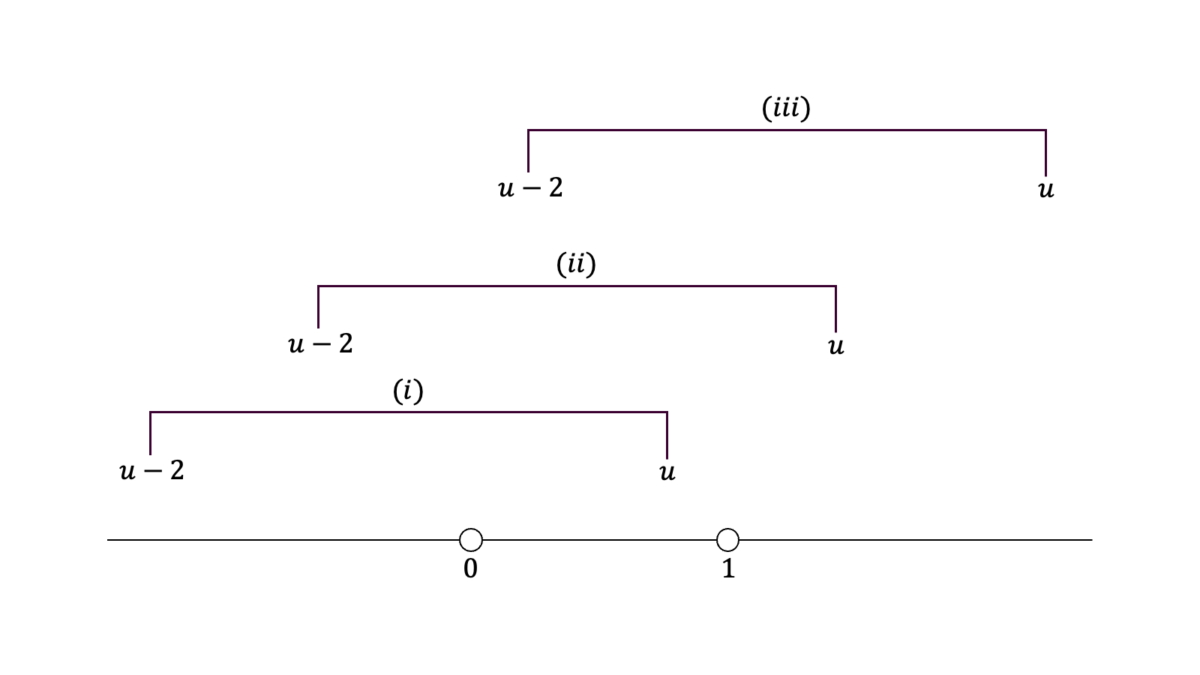
$D_{2}$の上限が$(0,1)$に含まれているとき,すなわち$0<u<1$のとき,
h(u) &= \int_{0}^{u}f(x)g(u-x)dx = \int_{0}^{u}\frac{1}{2}dx = \frac{u}{2}
\end{align}
となる。$D_{2}$に$D_{1}$が含まれているとき,すなわち$1<u<2$のとき,
h(u) &= \int_{0}^{1}f(x)g(u-x)dx = \int_{0}^{1}\frac{1}{2}dx = \frac{1}{2}
\end{align}
となる。$D_{2}$の下限が$(0,1)$に含まれているとき,すなわち$2<u<3$のとき,
h(u) &= \int_{u-2}^{1}f(x)g(u-x)dx = \int_{u-2}^{1}\frac{1}{2}dx = \frac{3-u}{2}
\end{align}
となる。それ以外の場合は$h(u)=0$となる。
$X,Y$が独立に$\U(0,1)$に従うとき$(X{+}Y,2X{-}Y)$の同時確率密度関数と周辺確率密度関数を求めよ。
$U{=}X{+}Y,V{=}2X{-}Y$とおく。逆変換は$X{=}(U{+}V)/3,Y{=}(2U{-}V)/3$でヤコビアンは$|J|{=}1/3$となるため,$X,Y$の確率密度関数を$f$,$U,V$の同時確率密度関数を$g$とおくと,$g{=}f((u{+}v)/3)f((2u{-}v)/3)$となる。$f$の定義域から,$g$の定義域$D$は$\{0{<}u{+}v{<}3\land 0{<}2u{-}v{<}3\}$となり,
g(u,v) &= f((u+v)/3)f((2u-v)/3) = \frac{1}{3}
\end{align}
となる。ただし,$D$の外では$g(u,v)=0$となる。周辺確率密度関数を求めるため,$D$を図示する。
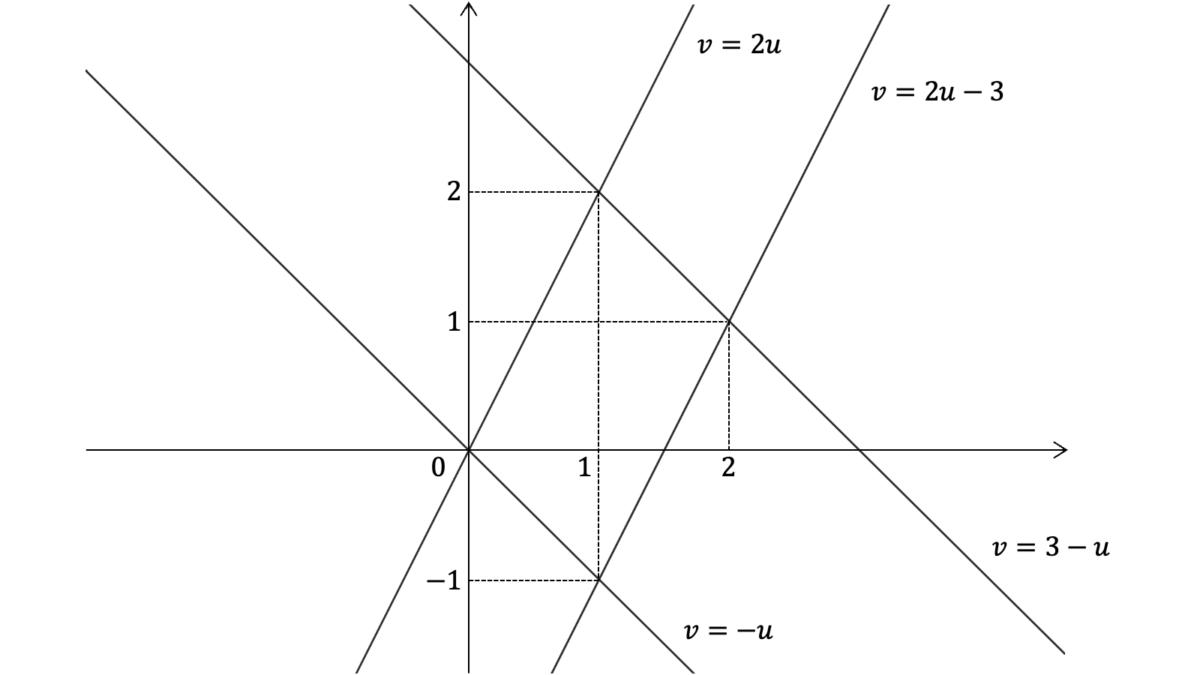
平行四辺形の内部が$D$である。$g(u)$を求める際は$v$を変数として周辺化するため,$u$軸に注目して$v$の取り得る値を$u$で表す。
| $u$の範囲 | $v$の取り得る値 | $g(u)$ |
|---|---|---|
| $0<u<1$ | $(-u, 2u)$ | $g(u)=\int_{-u}^{2u}1/3dv=u$ |
| $1<u<2$ | $(2u-3, 3-u)$ | $g(u)=\int_{2u-3}^{3-u}1/3dv=-u+2$ |
| 上記以外 | 上記以外 | $0$ |
同様に,$g(v)$を求める際は$u$を変数として周辺化するため,$v$軸に注目して$u$の取り得る値を$v$で表す。
| $v$の範囲 | $u$の取り得る値 | $g(v)$ |
|---|---|---|
| $-1<v<0$ | $(-v, (v+3)/2)$ | $g(u)=\int_{v}^{(v+3)/2}1/3du=(1+v)/2$ |
| $0<v<1$ | $(v/2,(v+3)/2)$ | $g(u)=\int_{v/2}^{(v+3)/2}1/3du=1/2$ |
| $1<v<2$ | $(v/2,3-v)$ | $g(u)=\int_{v/2}^{3-v}1/3du=(2-v)/2$ |
| 上記以外 | 上記以外 | $0$ |
$X,Y$が独立に$\U(0,1)$に従うとき,$XY$の同時確率密度関数を求めよ。
$X,Y$の確率密度関数を$f$とおくと,確率変数の四則と確率密度関数の関係より$U{=}XY$の確率密度関数$g$の被積分関数は$f(x)f(u/x)/|x|$となる。$f$の定義域より,$x$の取り得る値の範囲は第一項目について$D_{1}{=}(0,1)$であり,第二項目について$D_{2}{=}(u,1)$である。$x$の積分範囲は$D_{1}$と$D_{2}$の共通部分であるが,$U$の定義より$0{<}u{<}1$であるため,
g(u) &= \int_{u}^{1}f(x)f(u/x)/|x|dx = \int_{u}^{1}\frac{dx}{x} = -\log u
\end{align}
となる。
$X,Y$が独立に$\N(0,1)$に従うとき,$X/Y$の同時確率密度関数を求めよ。
$X,Y$の確率密度関数を$f$とおくと,確率変数の四則と確率密度関数の関係より$U{=}X/Y$の確率密度関数$g$の被積分関数は$f(uy)f(y)/|y|$となる。$f$の定義域より,$y$の取り得る値の範囲は第一項目について$u$を定数と見ることにより$D_{1}{=}(-\infty,\infty)$であり,第二項目についても$D_{2}{=}(-\infty,\infty)$である。$y$の積分範囲は$D_{1}$と$D_{2}$の共通部分であるが,$D_{1}{=}D_{2}$となっているため特に気にする必要はなく,
g(u) &= \int_{-\infty}^{\infty} f(uy)f(y)/|y|dy\\[0.7em]
&= \int_{-\infty}^{\infty}\left(\frac{e^{-(uy)^{2}/2}}{\sqrt{2\pi}}\right)\cdot \left(\frac{e^{-y^{2}/2}}{\sqrt{2\pi}}\right)dy\\[0.7em]
&= \frac{1}{\pi}\int_{0}^{\infty}e^{-(u^{2}+1)y^{2}/2}dy\\[0.7em]
&=\frac{1}{\pi}\left[-\frac{1}{u^{2}+1}e^{-(u^{2}+1)y^{2}/2}\right]_{0}^{\infty}
= \frac{1}{\pi(u^{2}+1)}
\end{align}
となる。
$X_{1},\ldots,X_{n}$が独立に同一分布に従うとき,$X_{(i)}$の確率密度関数を求めよ。
累積分布関数$F_{X_{(i)}}$は$P(X_{(i)}{\leq}x)$と表され,$X_{1},\ldots,X_{n}$のうち$x$以下となる確率変数が$i$個である確率を表している。各$X_{k}$は確率$F(x)$で$X_{k}{\leq}x$となることから,$F_{X_{(i)}}$は二項分布$\Bin(n,F(x))$に従うため,
F_{X_{(i)}}(x)
&= \sum_{k=i}^{n} {}_{n}C_{k}~F(x)^{k}\left\{1-F(x)\right\}^{n-k}
\equiv \sum_{k=i}^{n} g(n,k)
\end{align}
となる。ただし,$g(n,k)$は$0{\leq}k{\leq}n$上で定義される。$g(n{-}1,n)=0$に注意すると,$X_{(i)}$の確率密度関数は
f_{X_{(i)}}(x)
&= \frac{dF(x)}{dx}\frac{d F_{X_{(i)}}(x)}{dF(x)}\\[0.7em]
&= f(x)n\sum_{k=i}^{n}(g(n-1,k-1)-g(n-1,k))\\[0.7em]
&= nf(x)(g(n-1,i-1)-g(n-1,n))\\[0.7em]
&= nf(x)g(n-1,i-1)\\[0.7em]
&= nf(x){}_{n-1}C_{i-1}~F(x)^{i-1}\left\{1-F(x)\right\}^{n-i}
\end{align}
となる。
$X_{1},\ldots,X_{n}$が独立に同一分布に従うとき,第$1$および第$n$順序統計量の確率密度関数を求めよ。
前問の結果に$i=1$を代入することにより,$X_{(1)}=\min(X_{1},\ldots,X_{n})$の累積分布関数は
F_{X_{(1)}}(x) &= \sum_{k=1}^{n} g(n,k) = 1-g(n,0) = 1-\left\{1-F(x)\right\}^{n}
\end{align}
となり,確率密度関数は
f_{X_{(1)}}(x) &= nf(x){}_{n-1}C_{0}~F(x)^{0}\left\{1-F(x)\right\}^{n-1} = nf(x)\left\{1-F(x)\right\}^{n-1}
\end{align}
となる。同様に,$i=n$を代入することにより,$X_{(n)}=\max(X_{1},\ldots,X_{n})$の累積分布関数は
F_{X_{(n)}}(x) &= \sum_{k=n}^{n} g(n,k) = g(n,n) = F(x)^{n}
\end{align}
となり,確率密度関数は
f_{X_{(n)}}(x) &= nf(x){}_{n-1}C_{n-1}~F(x)^{n-1}\left\{1-F(x)\right\}^{0} = nf(x)F(x)^{n-1}
\end{align}
となる。
$X_{1},X_{2},X_{3}$が独立に$\U(0,1)$に従うとき,第$1$〜第$3$順序統計量の確率密度関数を求めよ。
前問の結果より,$0<x<1$上で$f(x)=1$と$F(x)=x$であることに注意すると,$X_{(1)}$の確率密度関数は
f_{X_{(1)}}(x) &= nf(x)\left\{1-F(x)\right\}^{n-1} = 3(1-x)^{2}
\end{align}
となり,$X_{(2)}$の確率密度関数は
f_{X_{(2)}}(x)
&= nf(x){}_{n-1}C_{i-1}~F(x)^{i-1}\left\{1-F(x)\right\}^{n-i}\\[0.7em]
&= 3f(x){}_{2}C_{1}~F(x)^{1}\left\{1-F(x)\right\}^{1}
= 6x(1-x)
\end{align}
となり,$X_{(3)}$の確率密度関数は
f_{X_{(3)}}(x) &= nf(x)F(x)^{n-1} = 3x^{2}
\end{align}
となる。
$X_{1},X_{2}$が$0{<}x{<}1$で独立に$f(x){=}2{-}2x$に従うとき,順序統計量の確率密度関数を求めよ。
前問の結果より,$F(x)=$$X_{(1)}$の確率密度関数は
f_{X_{(1)}}(x) &= nf(x)\left\{1-F(x)\right\}^{n-1}
= 2(2-2x)\left\{1-(2x-x^{2})\right\}
= -4(x-1)^{3}
\end{align}
となり,$X_{(2)}$の確率密度関数は
f_{X_{(2)}}(x) &= nf(x)F(x)^{n-1} = 2(2-2x)(2x-x^{2}) = 4x(x-1)(x-2)
\end{align}
となる。ただし,いずれも$0<x<1$である。
$0{<}x,y{<}1$かつ$x{+}y{<}1$上の$f(x,y){=}120xy(1{-}x{-}y)$に対し,$(X,Y)$の相関係数を求めよ。
$x$の周辺分布は
f(x) &= 120\int_{0}^{1-x}\{-xy^{2}-x(x-1)y\}dy = 20x(1-x)^{3}
\end{align}
であるため,原点周りの一次モーメントは
E[X] &= 20\int_{0}^{1}x^{2}(1-x)^{3}dx = \frac{1}{3}
\end{align}
であり,原点周りの二次モーメントは
E[X^{2}] &= 20\int_{0}^{1}x^{2}(1-x)^{3}dx = \frac{1}{7}
\end{align}
である。したがって,分散は
V[X] &= E[X^{2}]-E[X]^{2} = \frac{2}{63}
\end{align}
となる。対称性より,$V[Y]=2/63$となる。一方,$XY$の期待値は
E[XY] &= 120\int_{0}^{1}\int_{0}^{1-x}\{-x^{2}y^{3}-x^{2}(x-1)y^{2}\}dy = \frac{2}{21}
\end{align}
であるため,相関係数は
\rho(X,Y) &= \frac{E[XY]-E[X]E[Y]}{\sqrt{V[X]}\sqrt{V[Y]}} = \frac{2/21-1/9}{2/63} = -\frac{1}{2}
\end{align}
となる。
$|x{+}y|{<}1$かつ$|x{-}y|{<}1$上の$f(x,y){=}1/2$に対し,独立性と相関の関係を論ぜよ。
$y$の積分範囲は${-}x{-}1{<}y{<}1{-}x$かつ$x{-}1{<}y{<}1{+}x$となる。最小値に関して,$x{>}0$のときは$x{-}1$で$x{<}0$のときは${-}x{+}1$であるため,絶対値を用いて$|x|{-}1$と表される。同様に,最大値は$1{-}|x|$と表される。したがって,$x$の周辺分布は
f_{1}(x) &= \int_{|x|-1}^{1-|x|}\frac{1}{2}dy = 1-|x|
\end{align}
となる。対称性より,$y$の周辺分布$f_{2}$は$1-|y|$となる。$f_{1}(x)f_{2}(y)\neq 1/2$より,$(X,Y)$は独立ではない。一方,$-1<x<1$および$x(1-|x|)$が奇関数であることに注意すると,
E[X] &= \int_{-1}^{1}x(1-|x|)dx = 0
\end{align}
となる。対称性より,$E[Y]{=}0$となる。さらに,$x(1-|x|)^{2}$が奇関数であることに注意すると,
E[XY] &= \int_{-1}^{1}\int_{|x|-1}^{1-|x|}\frac{xy}{2}dydx = \int_{-1}^{1}x(1-|x|)^{2}dx = 0
\end{align}
となるため,$\Cov[X,Y]{=}E[XY]{-}E[X]E[Y]{=}0$となる。したがって,$(X,Y)$は無相関である。一般に独立ならば無相関となるが,無相関ならば独立は成り立たず,$f(x,y)$は後者の反例となっている。
$X,Y$が平均$\mu$分散$\sigma^{2}$の同一分布に独立に従うとき,$\rho(aX{+}bY,cX{+}dY)$を求めよ。
独立ならば無相関であることに注意すると,共分散の定義より,
C[aX+bY,cX+dY] &= E[\{a(X-\mu)+b(Y-\mu)\}\{c(X-\mu)+d(Y-\mu)\}]\\[0.7em]
&= (ac+bd)\sigma^{2}+(ad+bc)C[X,Y] = (ac+bd)\sigma^{2}
\end{align}
が得られる。一方,分散の性質より$V[aX{+}bY]{=}(a^{2}{+}b^{2})\sigma^{2}$と$V[cX{+}dY]{=}(c^{2}{+}d^{2})\sigma^{2}$が得られる。したがって,
\rho[aX+bY,cX+dY] &= \frac{(ac+bd)\sigma^{2}}{\sqrt{(a^{2}{+}b^{2})(c^{2}{+}d^{2})}\sigma^{2}}
= \frac{ac+bd}{\sqrt{(a^{2}{+}b^{2})(c^{2}{+}d^{2})}}
\end{align}
となる。
正規分布のモーメント母関数を標準正規分布のモーメント母関数から求めよ。
一般に,
M_{aX+b}(t) &= E[e^{t(aX+b)}] = e^{bt}E[e^{(at)X}] = e^{bt}M_{X}(at)
\end{align}
が成り立つ。$X{\sim}\N(0,1)$とすると,$\sigma X+\mu$は正規分布に従うため,
e^{\mu t}M_{X}(\sigma t) &= e^{\mu t}e^{\sigma^{2}t^{2}/2} = e^{\sigma^{2}t^{2}/2+\mu t}
\end{align}
が得られる。
$X{\sim}\N(0,1)$に対し,$n$次モーメント$E[X^{n}]$を求めよ。
$e^{x}$のマクローリン展開を用いて標準正規分布のモーメント母関数を展開することにより,
M_{X}(t) &= \sum_{k=0}^{\infty}\frac{t^{2k}}{2^{k}k!} = 1+\frac{t^{2}}{2^{1}1!}+\frac{t^{4}}{2^{2}2!}+\cdots
\end{align}
となる。したがって,
E[X^{n}] &= M^{(n)}_{X}(t) =
\begin{cases}
\displaystyle
\frac{n!}{2^{n/2}(n/2)!}&(n: \text{偶数})\\[0.7em]
0&(n: \text{奇数})
\end{cases}
\end{align}
が得られる。
$\N(\mu,\sigma^{2})$の歪度と尖度を求めよ。
$Y{=}aX+b$とおくと,
\frac{E[(Y{-}\mu_{Y})^{k}]}{V[Y]^{k/2}}
&{=} \frac{E[\{(aX+b){-}(a\mu_{X}+b)\}^{k}]}{V[aX+b]^{k/2}}
{=} \frac{a^{k}E[(X{-}\mu_{X})^{k}]}{a^{k}V[X]^{k/2}}
{=} \frac{E[(X{-}\mu_{X})^{k}]}{V[X]^{k/2}}
\end{align}
となることから,$aX+b$の歪度と尖度は$X$の歪度と尖度と一致する。したがって,正規分布の歪度と尖度は標準正規分布の歪度と尖度と等しく,直前の問題の結果を利用すると,
\frac{E[(Y{-}\mu_{Y})^{3}]}{V[Y]^{3/2}} = \frac{0}{1} = 0,\quad
\frac{E[(Y{-}\mu_{Y})^{4}]}{V[Y]^{4/2}} = \frac{3}{1} = 3
\end{align}
となる。ただし,正規分布の歪度と尖度を$0$とするため,尖度を$-3$して定義する流派もある。
三角分布のモーメント母関数を求めよ。
三角分布は$-1\leq x\leq 1$で定義され,確率密度関数は$1-|x|$であるため,
M(t) &{=} \int_{-1}^{1}e^{tx}(1-|x|)dx
{=} \left(\frac{1}{t}{-}\frac{1-e^{-t}}{t^{2}}\right)+\left(-\frac{1}{t}{-}\frac{1-e^{-t}}{t^{2}}\right)
{=} \frac{e^{t}+e^{-t}-2}{t^{2}}
\end{align}
となる。
$\U(0,1)$に独立に従う$X,Y$に対し,$X-Y$は三角分布に従うことを示せ。
一様分布のモーメント母関数より,
M_{X-Y}(t) &= M_{X}(t)M_{-Y}(t) = \frac{e^{t}-1}{t}\cdot \frac{e^{-t}-1}{t} = \frac{e^{t}+e^{-t}-2}{t}
\end{align}
となり,三角分布となる。
三角分布のモーメント母関数$M(t)$に対し,$M(2t)$が従う分布を求めよ。
前問で示した通り$M_{aX+b}(t){=}e^{bt}M_{X}(at)$となるため,$M(2t)$は$2X$が従う分布と等しくなる。三角分布の確率密度関数において$U{=}2X$と変数変換すると,$-2{\leq}u{\leq}0$および$0{\leq}u{\leq}2$に対して
f(u) &= \left(1\pm\frac{u}{2}\right)\cdot\frac{1}{2} = \frac{2\pm u}{4}
\end{align}
となるため,結局$f(u){=}(2{-}|u|)/4$が得られる。
具体的な確率分布
二項分布$\Bin(n,p)$の確率質量関数$f(x)$を最大にする$x$を求めよ。
\frac{f(k+1)}{f(k)} &= \frac{(n-k)p}{(k+1)q} \geq 1
\end{align}
を変形すると$k+1\leq (n+1)p$となるため,$r\leq (n+1)p<r+1$となる整数$r$をとれば
f(1)<\cdots<f(r-1)\leq f(r) > f(r+1)\cdots>f(n)
\end{align}
となる。したがって,$r$を$(n+1)p$の整数部分とすると,$f(x)$の最大値は,
\begin{cases}
f(r-1)=f(r)&(n+1)p\text{が整数のとき}\\[0.7em]
f(r)&(n+1)p\text{が整数でないとき}
\end{cases}
\end{align}
となる。
ポアソン分布$\Po(\lambda)$の確率質量関数$f(x)$を最大にする$x$を求めよ。
\frac{f(k+1)}{f(k)} &= \frac{\lambda}{k+1} \geq 1
\end{align}
を変形すると$k+1\leq \lambda$となるため,$r\leq \lambda<r+1$となる整数$r$をとれば
f(1)<\cdots<f(r-1)\leq f(r) > f(r+1)\cdots>f(n)
\end{align}
となる。したがって,$r$を$\lambda$の整数部分とすると,$f(x)$の最大値は,
\begin{cases}
f(r-1)=f(r)&\lambda\text{が整数のとき}\\[0.7em]
f(r)&\lambda\text{が整数でないとき}
\end{cases}
\end{align}
となる。
負の二項分布$\NB(r,p)$の確率質量関数$f(x)$を最大にする$x$を求めよ。
\frac{f(k+1)}{f(k)} &= \frac{r+k}{k+1} \geq 1
\end{align}
を変形すると$k+1\leq (r-1)q/(1-q)$となるため,$r\leq (r-1)q/(1-q)<r+1$となる整数$r$をとれば
f(1)<\cdots<f(r-1)\leq f(r) > f(r+1)\cdots>f(n)
\end{align}
となる。したがって,$r$を$(r-1)q/(1-q)$の整数部分とすると,$f(x)$の最大値は,
\begin{cases}
f(r-1)=f(r)&(r-1)q/(1-q)\text{が整数のとき}\\[0.7em]
f(r)&(r-1)q/(1-q)\text{が整数でないとき}
\end{cases}
\end{align}
となる。
負の二項分布を用いた例題とその答えを作成せよ。
勝率が$9$割の雀士が$18$勝するまでに$3$局以上負ける確率を求める。$\NB(r,p)$において$r=18$と大きく,かつ$p=9/10$と$1$に近いため,$p=1/(1+c)$より$c=1/9$であることに注意すると,$\lambda=rc=2$のポアソン分布で近似することができ,
P(X\geq 3) &= 1-\left(\frac{2^{0}e^{-2}}{0!}+\frac{2^{1}e^{-2}}{1!}+\frac{2^{2}e^{-2}}{2!}\right)
\end{align}
となる。
無記憶性をもつ離散型確率分布を論ぜよ。
無記憶性をもつ連続型確率分布は幾何分布である。いま,離散型確率分布が無記憶性をもつならば
P(X=i+k) &= P(X\geq i)P(X=k)
\end{align}
が成り立つ。$i=1$のとき,$P(X\geq i)=q$とおくと$P(X=k+1)=qP(X=k)$が成り立つ。これを逐次適用すれば$ P(X=k)=pq^{k}$が得られる。逆に,$X$がパラメータ$p$の幾何分布に従うとき,
P(X{=}i{+}k{|}X{\geq}i)&{=}\frac{P(X{=}i+k)}{P(X{\geq}i)}{=}\frac{pq^{i{+}k}}{pq^{i}{+}pq^{i{+}1}{+}{\cdots}} {=}\frac{q^{k}}{1{+}q{+}q^{2}{+}{\cdots}}{=}(1{-}q)q^{k}{=}pq^{k}
\end{align}
となり,無記憶性をもつ。
無記憶性をもつ連続型確率分布を論ぜよ。
無記憶性をもつ連続型確率分布は指数分布である。事象が生じる前に時間を$T$とし,時刻$t\geq 0$までに事象が起こらなかった場合に,続く$\Delta t$の間に事象が起きる確率が時刻$t$に依存しない性質を無記憶性という。具体的には,
p(t\leq T<t+\Delta t\mid t\leq T) &= K\Delta t
\end{align}
を満たす性質のことを指す。もしくは,
p(t+\Delta t<T|t<T) &= p(\Delta t<T)
\end{align}
と表されることもある。条件付き確率の定義を用いて変形すると,
\frac{p(t\leq T<t+\Delta t)}{p(T\geq t)}
&= \frac{F(t+\Delta t)-F(t)}{1-F(t)}
\approx \frac{F^{\prime}(t)\Delta t}{1-F(t)} = K\Delta t
\end{align}
となる。したがって,微分方程式を解くことにより$-\log(1-F(t))=Kt+C$となる。$F(0)=0$を代入して整理すると$e^{-C}=1$が得られ,$F(t)=1-e^{-Kt}$となる。両辺を微分することにより$f(t)=Ke^{-Kt}$が得られる。ただし,$t>0$である。逆に,$T$が指数分布に従うとき,$1-F(x)=e^{-Kt}$となることに注意すると,
p(t+\Delta t<T|t<T)
&{=} \frac{p(t+\Delta t<T)}{p(t<T)}
{=} \frac{e^{-K(t+\Delta t)}}{e^{-Kt}}
{=} e^{-K\Delta t}
{=} p(\Delta t<T)
\end{align}
となり,無記憶性をもつ。
$X$がパラメータ$p$の幾何分布に従うとき$p(X>i+k|X>i)=p(X\geq k)$が成り立つことを示せ。
$p=1-q$を用いて無限等比級数の形を出現させると,
p(X{>}i{+}k{|}X{>}i)
&{=}\frac{p^{i{+}k{+}1}p^{i{+}k{+}2}{\cdots}}{p^{i{+}1}p^{i{+}2}{\cdots}}
{=} q^{k}
{=} \frac{p}{p}q^{k}
{=} \frac{p}{1{-}q}q^{k}
{=} pq^{k}{+}pq^{k{+}1}{+}{\cdots}
{=} p(X{\geq}k)
\end{align}
が得られる。
超幾何分布の各標本の平均・分散・共分散と標本和の平均・分散を求めよ。
赤玉$N_{0}$個,白玉$N_{1}$個,合計$N$個とする。$X$を赤玉を取り出す事象に対応する確率変数とするとき,一回の試行はベルヌーイ試行であるから,
E[X_{i}]&=\frac{N_{0}}{N},\quad V[X_{i}]=\frac{N_{0}}{N}\left(1-\frac{N_{0}}{N}\right)
\end{align}
となる。定義より$E[X_{i}X_{j}]=1\cdot N_{0}(N_{0}-1)/(N(N-1))+0$となるため,
C[X_{i},X_{j}]
&= E[X_{i}X_{j}]-E[X_{i}]E[X_{j}]
= \frac{N_{0}(N_{0}-1)}{N(N-1)}{-}\left(\frac{N_{0}}{N}\right)^{2} = -\frac{N_{0}(N-N_{0})}{N^{2}(N-1)}
\end{align}
となる。$X=X_{1}+\cdots+X_{n}$とおくと,期待値の線形性より
E[X] &= \frac{nN_{0}}{N}
\end{align}
となり,分散の性質より
V[X] &= \sum_{i=1}^{n}V[X_{i}]+\sum_{i\neq j}C[X_{i},X_{j}] = \frac{nN_{0}N_{1}(N-n)}{N^{2}(N-1)}
\end{align}
となる。分散に関しては,別解として有限修正項を用いることにより,
V[X] &= \frac{N-n}{N-1}npq = n\frac{N-n}{N-1}\frac{N_{0}}{N}\frac{N_{1}}{N}
\end{align}
と求めることもできる。
5000個の製品から3%の不良品率で10個取り出すときに不良品が高々2個である確率を求めよ。
5000は十分大きいため,母集団の数は関係なく復元抽出とみなすことができ,
\sum_{i=0}^{2}{}_{10}C_{i}\left(\frac{3}{100}\right)^{i}\left(\frac{97}{100}\right)^{10-i}
\end{align}
と求められる。
書類数は$p{=}1/4$の幾何分布,$1$通の決済時間は$\Exp(1/2)$に従うとき,平均待ち時間を求めよ。
$k$通の決済時間の従う確率密度関数$f(x)$は指数分布の和であり,$\Gamma(k,\lambda)$となる。したがって,待ち時間の確率密度関数は$x>0$に対して
g(x)
&= \sum_{k=1}^{\infty}\frac{1}{4}\left(\frac{3}{4}\right)^{k}\frac{2^{k}}{(k-1)!}x^{k-1}e^{-2x}\\[0.7em]
&= \frac{3}{8}e^{-2x}\sum_{k=1}^{\infty}\frac{(3x/2)^{k-1}}{(k-1)!} = \frac{3}{8}e^{-2x}e^{3x/2} = \frac{3}{8}e^{-x/2}
\end{align}
となる。したがって,平均待ち時間は
E[X] &= \int_{0}^{\infty}x\cdot\frac{3}{8}e^{-x/2}dx = \frac{3}{2}
\end{align}
となる。
$i{=}1,\ldots,n$と$T_{i}{\sim}\Exp(1/\lambda_{i})$に対し,$T_{(1)}$の分布を述べよ。
例えば,時間間隔$T_{i}$で到着するタクシーに最初に乗る人の待ち時間が相当する。累積分布関数を考えると,
p(T_{(1)}\leq t)
&{=} 1{-}p(T_{(1)}>t)
{=} 1{-}p(T_{1}>t)p(T_{2}>t)\cdots p(T_{n}>t)
{=} 1{-}e^{{-}(\lambda_{1}+\cdots+\lambda_{n})t}
\end{align}
となるため,$f(t)=\lambda_{1}+\cdots+\lambda_{n}e^{{-}(\lambda_{1}+\cdots+\lambda_{n})t}$となる。
確率分布の関係
負の二項分布$\NB(r,p)$をポアソン分布$\Po(\lambda)$で近似せよ。
$r=\lambda/c$,$p=1/(1+c)$とおいて$c\rarr 0$とする。
f(x)
&= \lim_{c\rarr 0}\frac{(\lambda/c+x-1)!}{x!(\lambda/c)!}\left(\frac{1}{1+c}\right)^{\lambda/c}\left(\frac{c}{1+c}\right)^{x}\\[0.7em]
&= \lim_{c\rarr 0}\frac{1}{x!}(\lambda+(x-1)c)\cdots(\lambda+1)\lambda\{(1+c)^{c}\}^{-\lambda}(1+c)^{-x}\\[0.7em]
&= \frac{\lambda^{x}e^{-\lambda}}{x!}
\end{align}
超幾何分布を二項分布で近似せよ。
${}_{n}C_{k}$を出現させるイメージで変形する。
\frac{{}_{Np}C_{k}{}_{Nq}C_{n-k}}{{}_{N}C_{n}}
&= \frac{(Np)!}{k!(Np-k)!}\frac{(Nq)!}{(n-k)!(Np-n+k)!}\frac{n!(N-n)!}{N!}\\[0.7em]
&= \frac{n!}{k!(n-k)!}\frac{(Np)!(Nq)!(N-n)!}{(Np-k)!(Np-n+k)!N!}\\[0.7em]
&= {}_{n}C_{k}\frac{Np(Np{-}1)\cdots(Np{-}k+1)Nq(Nq{-}1)\cdots(Nq{-}n+k+1)}{N(N{-}1)\cdots(N{-}n+1)}\\[0.7em]
&= {}_{n}C_{k}\frac{p(p{-}1/N)\cdots(p{-}(k{-}1)/N)q(q{-}1/N)\cdots(q{-}(n{-}k{-}1)/N)}{(1{-}1/N)\cdots(1{-}(n{-}1)/N)}\\[0.7em]
&\rarr~{}_{n}C_{k}~p^{k}q^{n-k}\quad(N\rarr\infty)
\end{align}
三項分布の周辺分布は二項分布になることを示せ。
$x_{1}$を固定すると$x_{2}=0,1,\ldots,N-x_{1}$となるため,
p(X_{1}=x_{1})
&= \sum_{x_{2}=0}^{N-x_{1}}\frac{N!}{x_{1}!x_{2}!x_{3}!}p_{1}^{x_{1}}p_{2}^{x_{2}}p_{3}^{x_{3}}\\[0.7em]
&= \frac{N!}{n_{1}!(N-n_{1})!}p_{1}^{x_{1}}\sum_{x_{2}=0}^{N-x_{1}}\frac{(N-x_{1})!}{x_{2}!x_{3}!}p_{2}^{x_{2}}p_{3}^{x_{3}}\\[0.7em]
&= {}_{N}C_{x_{1}}p_{1}^{x_{1}}(p_{2}+p_{3})^{N-n_{1}}
\end{align}
が得られる。したがって,$X_{1}$は$\Bin(N,p_{1})$に従う。
三項分布の条件付き分布は二項分布になることを示せ。
条件付き確率の定義より,
P(X_{2}=x_{2}|X_{1}=x_{1}) &= \frac{P(X_{1}=x_{1},X_{2}=x_{2})}{P(X_{1}=x_{1})}\\[0.7em]
&= \frac{\{n!/\{x_{1}!x_{2}!x_{3}!)\}p_{1}^{x_{1}}p_{2}^{x_{2}}p_{3}^{x_{3}}}{\{n!/(x_{1}!(n-x_{1})!)\}p_{1}^{x_{1}}(1-p_{1})^{n-x_{1}}}\\[0.7em]
&= \frac{(n-x_{1})!}{x_{2}!x_{3}!}\frac{p_{2}^{x_{2}}p_{3}^{x_{3}}}{(1-p_{1})^{n-x_{1}}}\\[0.7em]
&= \frac{(x_{2}+x_{3})!}{x_{2}!x_{3}!}\frac{p_{2}^{x_{2}}p_{3}^{x_{3}}}{(p_{2}+p_{3})^{x_{2}+x_{3}}}\\[0.7em]
&= \frac{(x_{2}+x_{3})!}{x_{2}!x_{3}!}\left(\frac{p_{2}}{p_{2}+p_{3}}\right)^{x_{2}}\left(\frac{p_{3}}{p_{2}+p_{3}}\right)^{x_{3}}
\end{align}
が得られる。したがって,$X_{2}|X_{1}$は$\Bin(x_{2}+x_{3},p_{2}/(p_{2}+p_{3}))$に従う。
$X_{1},X_{2}$が平均$1/\lambda$の指数分布に従うとき,$X_{1}+X_{2}$の確率密度関数を求めよ。
ガンマ分布の定義より,$X_{1}+X_{2}$は$\Gamma(2,\lambda)$に従い,$x>0$に対して
f(x) &= \frac{\lambda^{2}}{\Gamma(2)}xe^{-\lambda x} = \lambda^{2}xe^{-\lambda x}
\end{align}
となる。別解として,愚直に変数変換する方法がある。確率変数の四則と確率密度関数の関係より,$f$の被積分関数は$f(u-v,v)=f(u-v)f(v)=\lambda^{2}e^{-\lambda u}$となる。$f(u-v)$の定義域から$v<u$であり,$f(v)$の定義域から$v>0$であるから,
f(u) &= \int_{0}^{u}\lambda^{2}e^{-\lambda u}dv = \lambda^{2}ue^{-\lambda u}
\end{align}
となる。
$X{\sim}\U(0,1)$のとき,$Y=-(\log X)/\lambda$の確率分布は何か。
$x\in[0,1]$より,$y\in[0,\infty)$である。$|dx/dy|=|{-}\lambda xdy|=\lambda e^{-\lambda y}$より,
f(y) &= 1\cdot \lambda e^{-\lambda y}=\lambda e^{-\lambda y}
\end{align}
となる。したがって,$\Exp(1/\lambda)$と等しくなる。
ポアソン分布の時間間隔が指数分布となることを示せ。
単位時間あたりに事象が起こる回数を$X$,期待値を$\lambda$とおくと,$(0,t]$における回数は
f(x) &= \frac{(\lambda t)^{x}}{x!}e^{-\lambda t}
\end{align}
に従う。事象が初めて起こるまでの待ち時間を$T$に対し,$p(T{>}t){=}f(x{=}0){=}e^{-\lambda t}$は$(0,t]$で事象が起こらない確率を表す。したがって,累積分布関数は
F(t) &= p(T\leq t) = 1-p(T>t) = 1-e^{-\lambda t}
\end{align}
と表され,$f(t)=F^{\prime}(t)=-\lambda e^{-\lambda t}$が得られる。
$X_{1},\ldots,X_{n}$が$\U(0,1)$に従うとき,$X_{(k)}$はベータ分布に従うことを示せ。
前問の順序統計量の確率密度関数より,
f_{X_{(k)}}(x)
&= n{}_{n-1}C_{k-1}x^{k-1}(1-x)^{n-k}\\[0.7em]
&= \frac{n!}{(k-1)!(n-k)!}x^{k-1}(1-x)^{n-k}\\[0.7em]
&= \frac{\Gamma(n+1)}{\Gamma(k)\Gamma(n-k+1)}x^{k-1}(1-x)^{n-k}\\[0.7em]
&= \frac{1}{B(k,n-k+1)}x^{k-1}(1-x)^{n-k}
\end{align}
となり,$\Be(k,n-k+1)$となることが示された。
$X{\sim}F(2n,2m)$に対し$Y{=}m/(m+nX)$のとき,$Y$が従う分布は何か。
$x=(m/n)(1/y-1)$より,ヤコビアンは$|dx/dy|=m/(ny^{2})$となる。したがって,$0<y<1$に対して
g(y)
&= \frac{(2m)^{m}(2n)^{n}}{B(m,n)}\frac{(m/n)^{n-1}((1-y)/y)^{n-1}}{(2m/y)^{n+m}}\frac{m}{ny^{2}}
= \frac{y^{m-1}(1-y)^{n-1}}{B(m,n)}
\end{align}
が成り立つ。すなわち,$Y\sim\Be(m,n)$となる。
$B(m,n)$の下側$100\alpha\%$点$B_{n}^{m}(1-\alpha)$と$F(2n,2m)$の下側$100\%$点$F_{2m}^{2n}(\alpha)$の関係を述べよ。
下側確率の定義より,$\beta=1-\alpha$とおくと,
B_{n}^{m}(1-\alpha)
&{=} p(Y\leq B_{n}^{m}(\beta))
{=} p\left(\frac{m}{m+nX}{\leq}B_{n}^{m}(\beta)\right)
{=} p\left(X{\geq}\frac{m}{n}\left(\frac{1}{B_{n}^{m}(\beta)}-1\right)\right)
\end{align}
となる。直前で示した結果より,
\frac{m}{n}\left(\frac{1}{B_{n}^{m}(\beta)}-1\right) &= F_{2m}^{2n}(\alpha)
\end{align}
となる。
$t$分布は$n\rarr\infty$で標準正規分布に収束することを示せ。
$t$分布の確率密度関数を変形すると,
f(t)
&= \frac{1}{\sqrt{n\pi}}\frac{\Gamma((n+1)/2)}{\Gamma(n/2)(n/2)^{1/2}}\left(\frac{n}{2}\right)^{1/2}
\left\{\left(1+\frac{t^{2}}{n}\right)^{n/t^{2}}\right\}^{-t^{2}/2}\left(1+\frac{t^2}{n}\right)^{-1/2}\\[0.7em]
&\rarr~\frac{1}{\sqrt{2\pi}}e^{-t^{2}/2}\quad(n\rarr\infty)
\end{align}
と示される。
記述統計と標本分布
最小二乗法で$(x_{1},y_{1}),\ldots,(x_{N},y_{N})$を直線にあてはめよ。
最小二乗法の目的関数は
J(a,b) &= \sum_{i=1}^{N}\left\{y_{i}-(ax_{i}+b)\right\}^{2}
\end{align}
となる。$a,b$で偏微分することにより,
\begin{cases}
\displaystyle
\frac{\partial J}{\partial a} = -2\sum_{i=1}^{N}\left\{y_{i}-(ax_{i}+b)\right\}x_{i} = 0\\
\displaystyle
\frac{\partial J}{\partial b} = -2\sum_{i=1}^{N}\left\{y_{i}-(ax_{i}+b)\right\} = 0
\end{cases}
\end{align}
が得られ,これにより,
\begin{cases}
\displaystyle
a\sum_{i=1}^{N}x_{i}^{2}+b\sum_{i=1}^{N}x_{i} = \sum_{i=1}^{N}x_{i}y_{i}\\
\displaystyle
a\sum_{i=1}^{N}x_{i}+bN = \sum_{i=1}^{N}y_{i}\\[0.7em]
\end{cases}
\end{align}
が得られる。ただし,二次式であるため最小値の存在は自明とした。これを$a$について解くと,
a &= \frac{N\sum_{i=1}^{N}x_{i}y_{i}-(\sum_{i=1}^{N}x_{i})(\sum_{i=1}^{N}y_{i})}{N\sum_{i=1}^{N}x_{i}^{2}-(\sum_{i=1}^{N}x_{i})^{2}} = \frac{N^{2}C[x,y]}{N^{2}\sigma^{2}_{x}} = \rho\frac{\sigma_{y}}{\sigma_{x}}
\end{align}
となり,$b$について解くと
b
&= \frac{N(\sum_{i=1}^{N}x^{2}_{i})(\sum_{i=1}^{N}y_{i})-(\sum_{i=1}^{N}x_{i})(\sum_{i=1}^{N}x_{i}y_{i})}{N\sum_{i=1}^{N}x_{i}^{2}-(\sum_{i=1}^{N}x_{i})^{2}}\\[0.7em]
&= \frac{N(\sigma^{2}_{x}+\barx^{2})N\bary-N\barx N(\rho\sigma_{x}\sigma_{y}+\barx\bary)}{N\sum_{i=1}^{N}x_{i}^{2}-(\sum_{i=1}^{N}x_{i})^{2}}
= \bary-\rho\frac{\sigma_{y}}{\sigma_{x}}\barx
\end{align}
が得られる。$y=ax+b$に代入すれば,
\frac{y-\bary}{\sigma_{y}} &= \rho\frac{x-\barx}{\sigma_{x}}
\end{align}
が得られる。$\rho$が正規化された標本の変化量のようなものを表していることも興味深い。
最小二乗法で$(x_{1},y_{1}),\ldots,(x_{N},y_{N})$を放物線にあてはめよ。
最小二乗法の目的関数は
J(a,b) &= \sum_{i=1}^{N}\left\{y_{i}-(ax_{i}^{2}+bx_{i}+c)\right\}^{2}
\end{align}
となる。$a,b,c$で偏微分することにより,
\begin{cases}
\displaystyle
\frac{\partial J}{\partial a} = -2\sum_{i=1}^{N}\left\{y_{i}-(ax_{i}^{2}+bx_{i}+c)\right\}x_{i}^{2} = 0\\
\displaystyle
\frac{\partial J}{\partial b} = -2\sum_{i=1}^{N}\left\{y_{i}-(ax_{i}^{2}+bx_{i}+c)\right\}x_{i} = 0\\
\displaystyle
\frac{\partial J}{\partial c} = -2\sum_{i=1}^{N}\left\{y_{i}-(ax_{i}^{2}+bx_{i}+c)\right\} = 0
\end{cases}
\end{align}
が得られ,これを整理すると
\begin{cases}
\displaystyle
a\sum_{i=1}^{n}x_{i}^{4}+b\sum_{i=1}^{n}x_{i}^{3}+c\sum_{i=1}^{n}x_{i}^{2} = \sum_{i=1}^{n}x_{i}^{2}y_{i}\\
\displaystyle
a\sum_{i=1}^{n}x_{i}^{3}+b\sum_{i=1}^{n}x_{i}^{2}+c\sum_{i=1}^{n}x_{i} = \sum_{i=1}^{n}x_{i}y_{i}\\
\displaystyle
a\sum_{i=1}^{n}x_{i}^{2}+b\sum_{i=1}^{n}x_{i}+cN = \sum_{i=1}^{n}y_{i}
\end{cases}
\end{align}
が得られる。ただし,最小値の存在は自明とした。直線へのあてはめとは異なり,この連立方程式の形で止めておくことが多い。
母平均・母分散と標本平均・標本分散の関係を述べよ。
$X_{1},\ldots,X_{n}$に対し,母平均は$E[X_{1}]=\cdots=E[X_{n}]$で標本平均は$E[X_{1}+\cdots+X_{n}]$である。母分散と標本分散も同様である。
標本分散の分散と不偏分散の分散の求め方を説明せよ。
標本を$Y_{i}{=}X_{i}{-}\mu$と標準化し,$V[S^{2}]{=}E[S^{4}]{-}E[S^{2}]^{2}$を利用する。$E[S^{4}]$を展開する際に,$E[Y_{i}]$を利用して非ゼロの値が出現する項の組み合わせを考える点がポイント。
標本分散の期待値を母分散で表せ。
$E[X_{i}-\mu]=0$と$E[\barX-\mu]=0$を利用して,
E[S^{2}]
&= E\left[\frac{1}{n}\sum_{i=1}^{n}(X_{i}{-}\barX)^{2}\right]
= \frac{1}{n}E\left[\sum_{i=1}^{n}(X_{i}{-}\mu)^{2}-\sum_{i=1}^{n}(\barX{-}\mu)^{2}\right]
= \frac{n-1}{n}\sigma^{2}
\end{align}
と表される。ただし,シグマの各要素について$E[(X_{i}-\mu)^{2}]=\sigma^{2}$と$V[\barX]=\sigma^{2}/n$を利用した。
$E[\barX^{2}]$と$E[(\barX-\mu)^{2}]$を求めよ。
$\mu_{n}^{\prime}=E[X^{n}]$とおく。$E[\barX^{2}]$については,
E[\barX^{2}]
&= \frac{1}{n^{2}}E\left[\left(\sum_{i=1}^{n}X_{i}\right)^{2}\right]\\[0.7em]
&= \frac{1}{n^{2}}\left\{E\left[\sum_{i=1}^{n}X_{i}^{2}\right]+2E\left[\sum_{i<j}^{n}X_{i}X_{j}\right]\right\}\\[0.7em]
&= \frac{{}_nC_{1}~\mu_{2}^{\prime}+2{}_nC_{2}~\mu^{2}}{n^{2}} = \frac{\mu_{2}^{\prime}+(n-1)\mu^{2}}{n}
\end{align}
と求められる。ただし,$i{<}j$なる$(i,j)$の選び方は,$2$つの$(X_{1}{+}{\cdots}{+}X_{n})$から$i$と$j$の選び方として$(i,j)$,$(j,i)$の$2$通り,数字の選び方として${}_nC_{2}$通り,選んだ数字の$(i,j)$への当てはめ方として$X_{i}{<}X_{j}$を満たす$1$通りとなっている。次に,$Y_{i}{=}X_{i}{-}\mu$とおく。
E[Y_{i}^{2}] &= \mu_{2}^{\prime}-2\mu \mu_{1}^{\prime}+\mu^{2} = \mu_{2}^{\prime}-\mu^{2}
\end{align}
および$E[Y_{i}Y_{j}]{=}E[Y_{i}]E[Y_{j}]{=}0$より,
E[(\barX-\mu)^{2}]
&= E\left[\left(\frac{1}{n}\sum_{i=1}^{n}(X_{i}-\mu)\right)^{2}\right]\\[0.7em]
&= \frac{1}{n^{2}}E\left[\left(\sum_{i=1}^{n}Y_{i}\right)^{2}\right]\\[0.7em]
&= \frac{1}{n^{2}}\left\{E\left[\sum_{i=1}^{n}Y_{i}^{2}\right]+2E\left[\sum_{i<j}^{n}Y_{i}Y_{j}\right]\right\}\\[0.7em]
&= \frac{n(\mu_{2}^{\prime}-\mu^{2})}{n^{2}}
= \frac{\mu_{2}^{\prime}-\mu^{2}}{n}
\end{align}
と求められる。
$E[\barX^{3}]$と$E[(\barX-\mu)^{3}]$を求めよ。
$\mu_{n}^{\prime}=E[X^{n}]$とおく。$E[\barX^{3}]$については,
E[\barX^{3}]
&{=} \frac{1}{n^{3}}E\left[\left(\sum_{i=1}^{n}X_{i}\right)^{3}\right]\\[0.7em]
&{=} \frac{1}{n^{3}}\left\{E\left[\sum_{i=1}^{n}X_{i}^{3}\right]+3E\left[\sum_{i\neq j}^{n}X_{i}^{2}X_{j}\right]+6E\left[\sum_{i<j<k}^{n}X_{i}X_{j}X_{k}\right]\right\}\\[0.7em]
&{=} \frac{{}_nC_{1}~\mu_{3}^{\prime}+6{}_nC_{2}~\mu_{2}^{\prime}\mu+6{}_nC_{3}~\mu^{3}}{n^{3}}
{=} \frac{\mu_{3}^{\prime}+3(n-1)\mu_{2}^{\prime}\mu+(n-1)(n-2)\mu^{3}}{n^{2}}
\end{align}
と求められる。ただし,$i{\neq}j$なる$(i,j)$の選び方は,$3$つの$(X_{1}{+}{\cdots}{+}X_{n})$から$i$と$j$の選び方として$(i,i,j)$,$(i,j,i)$,$(j,i,i)$の$3$通り,数字の選び方として${}_nC_{2}$通り,選んだ数字の$(i,j)$への当てはめ方として$2$通りとなっている。同様に,$i<j<k$なる$(i,j,k)$の選び方は,$3$つの$(X_{1}{+}{\cdots}{+}X_{n})$から$i$と$j$と$k$の選び方として$(i,j,k)$,$(i,k,j)$,$(j,i,k)$,$(j,k,i)$,$(k,i,j)$,$(k,j,i)$の$6$通り,数字の選び方として${}_nC_{3}$通り,選んだ数字の$(i,j,k)$への当てはめ方として$X_{i}{<}X_{j}{<}X_{j}$を満たす$1$通りとなっている。次に,$Y_{i}{=}X_{i}{-}\mu$とおく。
E[Y_{i}^{3}]
&= \mu_{3}^{\prime}-3\mu_{2}^{\prime}\mu+3\mu_{1}^{\prime}\mu^{2}-\mu^{3}
= \mu_{3}^{\prime}-3\mu_{2}^{\prime}\mu+2\mu^{3}
\end{align}
および$E[Y_{i}^{2}Y_{j}]{=}E[Y_{i}^{2}]E[Y_{j}]{=}0$および$E[Y_{i}Y_{j}Y_{k}]{=}E[Y_{i}]E[Y_{j}]E[Y_{k}]{=}0$より,
E[(\barX-\mu)^{3}]
&= E\left[\left(\frac{1}{n}\sum_{i=1}^{n}(X_{i}-\mu)\right)^{3}\right]\\[0.7em]
&= \frac{1}{n^{3}}E\left[\left(\sum_{i=1}^{n}Y_{i}\right)^{2}\right]\\[0.7em]
&= \frac{1}{n^{3}}\left\{E\left[\sum_{i=1}^{n}Y_{i}^{3}\right]+3E\left[\sum_{i\neq j}^{n}Y_{i}^{2}Y_{j}\right]+6E\left[\sum_{i<j<k}^{n}Y_{i}Y_{j}Y_{k}\right]\right\}\\[0.7em]
&= \frac{n(\mu_{3}^{\prime}-3\mu_{2}^{\prime}\mu+2\mu^{3})}{n^{3}}
= \frac{\mu_{3}^{\prime}-3\mu_{2}^{\prime}\mu+2\mu^{3}}{n^{2}}
\end{align}
と求められる。
$\N(0,1)$に独立に従う確率変数が$Y$の直交変換で表されるとき$Y$は$\N(0,1)$に独立に従うことを示せ。
直交変換を$T$とおく。$X=(X_{1},\ldots,X_{n})^{T}$および$Y=(Y_{1},\ldots,Y_{n})^{T}$とおくと,$X=TY$と表される。直交行列の行列式は$1$となり,標準正規分布の指数部分について
x_{1}^{2}+\cdots+x_{n}^{2} &= X^{T}X = Y^{T}T^{T}TY = Y^{T}Y = y_{1}^{2}+\cdots+y_{n}^{2}
\end{align}
となるため,直交変換後も標準正規分布で表される。
$X,Y$が独立に$\N(\mu,\sigma^{2})$に従うとき,$X+Y$と$X-Y$は独立であることを示せ。
前問において直交変換として
T &=
\frac{1}{\sqrt{2}}
\begin{bmatrix}
1&1\\
1&-1
\end{bmatrix}
\end{align}
を選ぶことにより,
\begin{bmatrix}
(X-\mu)/\sigma\\
(Y-\mu)/\sigma
\end{bmatrix}
&=
T
\begin{bmatrix}
(X+Y-\mu)/(\sqrt{2}\sigma)\\
(X-Y)/(\sqrt{2}\sigma)
\end{bmatrix}
\end{align}
と表されるため,$X+Y$と$X-Y$は独立になる。
$X,Y$が独立同一分布に従うとき,$X+Y$と$X-Y$が独立とならない例を示せ。
例えば$X,Y$が$\U(0,1)$に従うとする。$U{=}X+Y$は$0<u<2$に対して$g(u){=}1{-}|1{-}u|$に従い,$V{=}X{-}Y$は$-1{<}v{<}1$に対して$h(v){=}1{-}|v|$に従う。$0{<}u{+}v{<}2$と$0{<}u{-}v{<}2$に対して$f(u,v){=}1/2$であるが,明らかに$g(u)h(v)$と一致しないため,$(U,V)$は独立ではない。
$\N(0,1)$の標本に対し$\barX$と$S^{2}$が独立であることを示せ。
恣意的だが,恒等式
X_{1}^{2}+\cdots+X_{n}^{2} &= n\barX^{2}+\sum_{i=1}^{n}(X_{i}-\barX)^{2}
\end{align}
を考える。前問で示した通り,直交変換$T$により左辺は$Y_{1}^{2}+\cdots+Y_{n}^{2}$にうつされる。$T$として第一列の要素がすべて$1/\sqrt{1}$の行列を考える。このとき,グラムシュミットの正規直交化法により$T$が存在することが分かる。さらに,直交行列では全ての列ベクトルが直交しているため,
T &=
\begin{bmatrix}
1/\sqrt{n}&1/\sqrt{1\cdot 2}&1/\sqrt{2\cdot 3}&\cdots&1/\sqrt{(n-1)n}\\
1/\sqrt{n}&-1/\sqrt{1\cdot 2}&1/\sqrt{2\cdot 3}&\cdots&1/\sqrt{(n-1)n}\\
1/\sqrt{n}&0&-2/\sqrt{2\cdot 3}&\cdots&1/\sqrt{(n-1)n}\\
\vdots&\vdots&\vdots&&\vdots\\
1/\sqrt{n}&0&0&\cdots&-(n-1)/\sqrt{(n-1)n}\\
\end{bmatrix}
\end{align}
となっていることが分かる。したがって,$n\barX^{2}$は
nT\barX^{2}
&= n\left\{\frac{1}{n}\left(\frac{Y_{1}}{\sqrt{n}}+\cdots+\frac{Y_{1}}{\sqrt{n}}\right)\right\}
= Y_{1}^{2}
\end{align}
にうつされる。よって,
\sum_{i=1}^{n}(X_{i}-\barX)^{2} &= Y_{2}^{2}+\cdots+Y_{n}^{2}
\end{align}
が示される。前問より,$Y_{1},\ldots,Y_{n}$は独立に$\N(0,1)$に従うため,$Y_{1}^{2}$と$Y_{2}^{2}+\cdots+Y_{n}^{2}$は独立である。すなわち,$n\barX^{2}$と$nS^{2}$は独立となるため,$\barX^{2}$と$S^{2}$は独立となる。
$\N(0,1)$の標本に対し$n\barX^{2}$と$\sum_{i=1}^{n}(X_{i}-\barX)^{2}$はそれぞれ$\chi^{2}(1)$と$\chi^{2}(n-1)$に従うことを示せ。
前問より,$n\barX^{2}{=}Y_{1}^{2}$は$\chi^{2}(1)$に従い,$\sum_{i=1}^{n}(X_{i}{-}\barX)^{2}{=}Y_{2}^{2}{+}{\cdots}{+}Y_{n}^{2}$は$\chi^{2}(n-1)$に従う。
$\barX$と$S^{2}$が独立とならない例を挙げよ。
$n=2$とし,前問と同様に$X_{1},X_{2}$が$\U(0,1)$に従うとする。$\barX$と$S^{2}$が独立であると仮定すると,定義から$(X_{1}+X_{2})/2$と$\{(X_{1}-X_{2})/2\}^{2}$が独立となるが,これは前問の結果より$X_{1}+X_{2}$と$X_{1}-X_{2}$が独立とはならないという結果に矛盾する。したがって,$\barX$と$S^{2}$は独立ではない。
$\N(\mu,\sigma^{2})$の標本に対し$n\sum_{i=1}^{n}(X_{i}-\barX)^{2}/\sigma^{2}$は$\chi^{2}(n-1)$に従うことを示せ。
$Y_{i}{=}(X_{i}{-}\mu)/\sigma{\sim}\N(0,1)$となる。$S^{2}{=}Y_{1}^{2}{+}{\cdots}{+}Y_{n}$に対し,前問の結果より$n\sum_{i=1}^{n}(X_{i}{-}\barX)^{2}/\sigma^{2}{=}S^{2}$は$\chi^{2}(n{-}1)$に従う。
$\N(\mu,\sigma^{2})$の標本に対し$n\sum_{i=1}^{n}(X_{i}-\mu)^{2}/\sigma^{2}$は$\chi^{2}(n)$に従うことを示せ。
$Y_{i}{=}(X_{i}{-}\mu)/\sigma{\sim}\N(0,1)$となるが,$S^{2}{=}Y_{1}^{2}{+}{\cdots}{+}Y_{n}$は$\chi^{2}(n)$に従うというカイ二乗分布の定義そのものである。
$\N(0,1)$の標本に対し$(X_{1}{+}{\cdots}{+}X_{n})^{2}/n$が従う分布を述べよ。
正規分布の再生性より$\sum X_{i}$は$\N(0,n)$に従うため,$\sum X_{i}/\sqrt{n}$は$\N(0,1)$に従う。よって,$(\sum X_{i}/\sqrt{n})^{2}$は$\chi^{2}(1)$に従う。ただし,$n$個の和だからといって$\chi^{2}(n)$に従うと早とちりしないように気を付ける。あくまでも一つの変数の二乗を考えている。
$\N(0,1)$の標本に対し$(X_{1}{+}{\cdots}{+}X_{r})^{2}/r{+}(X_{r+1}{+}{\cdots}{+}X_{n})^{2}/(n{-}r)$が従う分布を述べよ。
前問の結果とカイ二乗分布の再生性を利用すれば,$\chi^{2}(2)$に従うことがわかる。他にも,例えば
\sum_{i=1}^{r}(X_{i}-\barX_{1})^{2}+\sum_{i=r+1}^{n}(X_{i}-\barX_{2})^{2}
\end{align}
が従う分布を考えると勉強になる。ただし,$\barX_{1}=\sum_{i=1}^{r}X_{i}/r$および$\barX_{2}=\sum_{i=r+1}^{n}X_{i}/(n-r)$とおいた。同様に考えれば,第一項目が$\chi^{2}(r-1)$に従い,第二項目が$\chi^{2}(n-r-1)$に従うため,カイ二乗分布の再生性より$\chi^{2}(n-2)$に従うことがわかる。
$\N(0,1)$の標本に対し$T{=}(\barX{-}\mu)/\sqrt{U^{2}/n}$が従う分布を述べよ。
$V=(n-1)U^{2}/\sigma^{2}$とおいて$T$を変形すると
T &= \frac{\barX-\mu}{\sqrt{U^{2}/n}} = \frac{\barX-\mu}{\sigma\sqrt{1/n}}/\sqrt{\frac{V}{n-1}}
\end{align}
となる。分子が$\N(0,1)$に,$V$は$\chi^{2}(n-1)$に従うため,$T\sim t(n-1)$となる。
$\N(0,1)$の標本に対し$T{=}((\barX_{1}{-}\barX_{2}){-}(\mu_{1}{-}\mu_{2}))/\sqrt{(1/n_{1}{+}1/n_{2})U^{2}}$が従う分布を述べよ。
まず,$U^{2}$は
U^{2} &= \frac{(n_{1}-1)U_{1}^{2}+(n_{2}-1)U_{2}^{2}}{n_{1}+n_{2}-2}
\end{align}
と計算されるとする。すると,前問と同様に$V=(n_{1}+n_{2}-1)U^{2}/\sigma^{2}$とおいて$T$を変形すると
T
&= \frac{(\barX_{1}-\barX_{2})-(\mu_{1}-\mu_{2})}{\sqrt{(1/n_{1}+1/n_{2})U^{2}}}\\[0.7em]
&= \frac{(\barX_{1}-\barX_{2})-(\mu_{1}-\mu_{2})}{\sigma\sqrt{(1/n_{1}+1/n_{2})}}/\sqrt{\frac{V}{n_{1}+n_{2}-1}}
\end{align}
となる。分子が$\N(0,1)$に,$V$は$\chi^{2}(n_{1}+n_{2}-2)$に従うため,$T\sim t(n_{1}+n_{2}-2)$となる。
不偏分散の比$T{=}U_{1}^{2}/U_{2}^{2}$は$F(n_{1}-1,n_{2}-1)$に従うことを示せ。
$(n_{1}-1)U_{1}^{2}/\sigma^{2}$と$(n_{2}-1)U_{2}^{2}/\sigma^{2}$は独立で,それぞれ$\chi^{2}(n_{1}-1)$と$\chi^{2}(n_{2}-1)$に従う。したがって,分散比$T=(U_{1}^{2}/\sigma^{2})/(U_{2}^{2}/\sigma^{2})$は$F(n_{1}-1,n_{2}-1)$に従う。
$X{\sim}t(n)$に対し,$X^{2}{\sim}F(1,n)$を示せ。
$T$分布に従う$X$は$Z{\sim}\N(0,1)$と$Y{\sim}\chi^{2}(n)$を用いて$Z/\sqrt{Y/n}$と表されるため,$X^{2}{=}Z^{2}/(Y/n)$となる。$Z^{2}$は$\chi^{2}(1)$に従うことに注意すると,$X{\sim}F(1,n)$であることが分かる。
$X{\sim}F(m,n)$に対し,$1/X{\sim}F(n,m)$を示せ。
$F$分布に従う$X$は$U{\sim}\chi^{2}(m)$と$V{\sim}\chi^{2}(n)$を用いて$(U/m)/(V/n)$と表されるため,$1/X$は$(V/n)/(U/m)$となる。$F$分布の定義より,$1/X{\sim}F(n,m)$であることが分かる。
二項分布下側確率と$F$分布の上側確率の関係を述べよ。
恣意的だが,$p>0,q>0,p+q=1$に対して都合のよい部分積分を考えることにより,
I
&= \frac{n!}{k!(n-k-1)!}\int_{p}^{1}t^{k}(1-t)^{n-k-1}dt\\[0.7em]
&= \frac{n!}{k!(n-k-1)!}\left[\frac{-t^{k}(1-t)^{n-k}}{n-k}\right]_{p}^{1}+\frac{n!}{(k-1)!(n-k)!}\int_{p}^{1}t^{k}(1-t)^{n-k}dt\\[0.7em]
&= {}_{n}C_{k}p^{k}q^{n-k}+{}_{n}C_{k-1}p^{k-1}q^{n-k+1}+\cdots+{}_{n}C_{0}p^{0}q^{n}
\end{align}
のように二項分布の形が出現する。いま,$m_{1}=2(k+1)$,$m_{2}=2(n-k)$,$F=m_{2}p/(m_{1}q)$とし,$t=(m_{1}x/(m_{1}x+m_{2}))$とおくと,
I
&{=} \frac{1}{B(m_{1}/2,m_{2}/2)}\int_{F}^{\infty}
\left(\frac{m_{1}x}{m_{1}x+m_{2}}\right)^{m_{1}/2-1}
\left(\frac{m_{2}}{m_{1}x+m_{2}}\right)^{m_{2}/2-1}
\frac{m_{1}m_{2}dx}{(m_{1}x+m_{2})^{2}}\\[0.7em]
&{=} \int_{F}^{\infty}
\frac{m_{1}^{m_{1}/2}m_{2}^{m_{2}/2}}{B(m_{1}/2,m_{2}/2)}
\frac{x^{m_{1}/2-1}}{(m_{1}x+m_{2})^{(m_{1}+m_{2})/2}}dx
\end{align}
となり,$i{=}0,{\ldots},k$における二項分布の下側確率と$[F,\infty)$における$F$分布の上側確率は等しくなる。
カイ二乗分布の上側確率とポアソン分布の関係を述べよ。
部分積分を次々に行うことでポアソン分布の確率質量関数の形を出現させる。
I
&= \frac{1}{k!}\int_{\lambda}^{\infty}t^{k}e^{-t}dt
= \frac{\lambda^{k}e^{-\lambda}}{k!}+\frac{1}{(k-1)!}\int_{\lambda}^{\infty}t^{k-1}e^{-t}dt
= \cdots = \sum_{i=0}^{k}\frac{\lambda^{ie^{-\lambda}}}{i!}
\end{align}
一方,$I$において$t=x/2$とおけば,
I
&= \frac{1}{(n/2-1)!}\int_{2\lambda}^{\infty}\left(\frac{x}{2}\right)^{n/2-1}e^{-x/2}\frac{dx}{2}
= \int_{2\lambda}^{\infty}f_{n}(x)dx
\end{align}
となるため,$I$はカイ二乗分布の上側確率で表される。
有限母集団の非復元抽出で得られた$X_{1},\ldots,X_{n}$の相関係数を求めよ。
母集団の元を$a_{1},\ldots,a_{N}$とし,母平均を$\mu$,母分散を$\sigma^{2}$とすると,標本平均と標本分散は
\begin{cases}
\displaystyle
E[X_{i}] = \sum_{r=1}^{N}a_{r}p(X_{i}=a_{r}) = \sum_{r=1}^{N}a_{r}\frac{1}{N} = \frac{1}{N}\sum_{r=1}^{N}a_{r} = \mu\\[0.7em]
\displaystyle
V[X_{i}] = \sum_{r=1}^{N}(a_{r}-\mu)^{2}p(X_{i}=a_{r}) = \sum_{r=1}^{N}(a_{r}-\mu)^{2}\frac{1}{N} = \frac{1}{N}\sum_{r=1}^{N}(a_{r}-\mu)^{2} = \sigma^{2}
\end{cases}
\end{align}
と表される。さらに,$p(X_{i}=a_{r},X_{j}=a_{s})=1/(N(N-1))$に注意すると,共分散は
C[X_{i},X_{j}] &= E[(X_{i}-\mu)(X_{j}-\mu)]\\[0.7em]
&= \sum_{r\neq s}^{n}(a_{r}-\mu)(a_{s}-\mu)p(X_{i}=a_{r},X_{j}=a_{s})\\[0.7em]
&= \frac{1}{N(N-1)}\left(\sum_{r=1}^{N}\sum_{s=1}^{N}(a_{r}-\mu)(a_{s}-\mu)-\sum_{r=1}^{N}(a_{r}-\mu)^{2}\right)\\[0.7em]
&= \frac{1}{N(N-1)}\left\{\left(\sum_{r=1}^{N}(a_{r}-\mu)\right)^{2}-\sum_{r=1}^{N}(a_{r}-\mu)^{2}\right\}\\[0.7em]
&= \frac{1}{N(N-1)}(0-N\sigma^{2}) = \frac{-\sigma^{2}}{N-1}
\end{align}
と表されるため,相関係数は$C[X_{i},X_{j}]/(\sqrt{V[X_{i}]}\sqrt{V[X_{j}]})=-1/(N-1)$と表される。
有限母集団の非復元抽出で得られた標本平均の期待値と分散,および標本分散の期待値を求めよ。
標本平均$\barX$の期待値に関して,
E[\barX] &= E\left[\frac{1}{n}\sum_{i=1}^{n}X_{i}\right] =\frac{1}{n} E\left[\sum_{i=1}^{n}X_{i}\right] = \mu
\end{align}
となる。標本平均$\barX$の分散に関して,前問の結果から$C[X_{i},X_{j}]{=}-\sigma^{2}/(N-1)$を用いると,
V[\barX]
&= E\left[(\barX-E[\barX])^{2}\right]\\[0.7em]
&= E\left[\left(\frac{1}{n}\sum_{i=1}^{n}(X_{i}-\mu)\right)^{2}\right]\\[0.7em]
&= \frac{1}{n^{2}}\left\{E\left[\sum_{i=1}^{n}(X_{i}-\mu)^{2}\right]+E\left[\sum_{i\neq j}^{n}(X_{i}-\mu)(X_{j}-\mu)\right]\right\}\\[0.7em]
&= \frac{1}{n^{2}}\left\{V[X_{i}]+n(n-1)C[X_{i},X_{j}]\right\}\\[0.7em]
&= \frac{1}{n^{2}}\left(n\sigma^{2}+\frac{n(n-1)}{N(N-1)}\sigma^{2}\right)
= \frac{N-n}{N-1}\frac{\sigma^{2}}{n}
\end{align}
となる。ただし,復元抽出とみなした場合の標本平均の分散$V[\barX]{=}\sigma^{2}/n$に有限修正項$(N{-}n)/(N{-}{1})$を利用してもよい。標本分散$S^{2}$の期待値について,$E[(X_{i}-\mu)]{=}0$と$E[(\barX-\mu)]{=}0$より,
E[S^{2}]
&= E\left[\frac{1}{n}\sum_{i=1}^{n}(X_{i}-\barX)^{2}\right]\\[0.7em]
&= \frac{1}{n}E\left[\sum_{i=1}^{n}(X_{i}-\mu)^{2}\right]-E\left[(\barX-\mu)^{2}\right]\\[0.7em]
&= \frac{n\sigma^{2}}{n}-V[\barX] = \left(1-\frac{N-n}{n(N-1)}\right)\sigma^{2} = \frac{N}{N-1}\frac{n-1}{n}\sigma^{2}
\end{align}
となる。
点推定
4つの代表的な推定量をまとめよ。
| 基準 | 定義 | 意味 |
|---|---|---|
| 不偏推定量 | $E[T]=\theta$ | 平均すると真の母数に等しい |
| 有効推定量 | 不偏推定量のうち,分散が最小の$T$ | 不偏推定量は分散が小さい方がよい |
| 一致推定量 | 任意の$\varepsilon$に対し$\lim_{n\rarr\infty}P(|T-\theta|<\varepsilon)=1$ | 標本を増やせば精度を上げられる |
| 十分推定量 | $\prod_{i=1}^{n}f(x_{i};\theta)=g(t;\theta)h(x_{1},\ldots,x_{n})$ | 母数の情報をすべて含んでいる |
ただし,十分推定量の定義はフィッシャー・ネイマンの分解定理によるものである。
クラメール・ラオの不等式を説明せよ。
母集団分布$f(x;\theta)$と$\theta$の推定量$T$に対し,微分と積分が交換可能であるという正則条件のもと,
V[T] \geq \cfrac{1}{nE\left[\left(\cfrac{\partial}{\partial \theta}f(x;\theta)\right)^{2}\right]}
\end{align}
が成り立つ。特に,等号が成立するならば$T$は$\theta$の有効推定量となる。$f$が二階微分可能であれば,
V[T] \geq \cfrac{1}{-nE\left[\cfrac{\partial^{2}}{\partial \theta^{2}}f(x;\theta)\right]}
\end{align}
となる。
最尤推定量と有効推定量の関係を述べよ。
有効推定量の存在を仮定するとき,すなわちクラメール・ラオの不等式で等号を満たすような推定量が存在するならば,最尤推定量は有効推定量に一致する。
最尤推定量と十分推定量の関係を述べよ。
十分推定量が存在すれば,最尤推定量は十分統計量の関数となる。
$\sum_{i=1}^{n}a_{i}=1$の条件下における$\sum_{i=1}^{n}a_{i}^{2}$の最小値を求めよ。
シュワルツの不等式
\left(\sum_{i=1}^{n}a_{i}^{2}\right)\left(\sum_{i=1}^{n}b_{i}^{2}\right)\geq \left(\sum_{i=1}^{n}a_{i}b_{i}\right)^{2}
\end{align}
において$b_{1}{=}{\cdots}{=}b_{n}{=}1$とおけば,等号成立条件$a_{1}/b_{1}{=}{\cdots}{=}a_{n}/b_{n}$より$a_{1}{=}{\cdots}{=}a_{n}{=}1/n$のとき最小値$1/n$となる。
$\U(0,\theta)$からの標本に対し,$T{=}\alpha_{n}\max\{X_{1},\ldots,X_{n}\}$が$\theta$の不偏推定量となるような$\alpha_{n}$は何か。
$\max\{X_{1},\ldots,X_{n}\}{=}X$とおくと,$E[\alpha_{n}X]{=}\theta$となる$\alpha_{n}$を求めればよい。順序推定量の確率密度関数より,$f(x){=}nf(x)F(x)^{n-1}{=}nx^{n-1}/\theta^{n}$となるため,
E[\alpha_{n}X] &= \alpha_{n}\int_{0}^{\theta}\frac{nx^{n}}{\theta^{n}} = \frac{n}{n+1}\alpha_{n}\theta
\end{align}
となる。したがって,$\alpha_{n}=(n+1)/n$となる。
$\Exp(1/\mu)$からの標本に対し,$T{=}n\barX^{2}/(n+1)$は$\mu^{2}$の不偏推定量であることを示せ。
期待値の定義を部分積分により計算することにより,$X{\sim}\Exp(1/\mu)$に対し$E[X^{2}]{=}2\mu^{2}$となるため,
E\left[\frac{n}{n+1}\barX^{2}\right]
&= \frac{1}{n(n+1)}\left\{E\left[\sum_{i=1}^{n}X_{i}^{2}\right]+E\left[\sum_{i\neq j}X_{i}X_{j}\right]\right\}\\[0.7em]
&= \frac{1}{n(n+1)}(2n\mu^{2}+n(n-1)\mu^{2}) = \mu^{2}
\end{align}
となる。
$\N(\mu,\sigma^{2})$の標本分散$S^{2}$に対し,$T{=}f(S)$が不偏推定量であることを示す方針を説明せよ。
$X{=}nS^{2}/\sigma^{2}$は$\chi^{2}(n-1)$に従うことを利用し,定義より$E[S]{=}\sigma E[\sqrt{X}]/\sqrt{n}$を計算する。
母平均既知の$\N(\mu_{0},\sigma^{2})$に対し,標本分散$S_{0}^{2}$は$\sigma^{2}$の不偏推定量であることを示せ。
期待値の中身を展開して証明すればよい。
E[S_{0}^{2}]
&= \frac{1}{n}E\left[\sum_{i=1}^{n}X_{i}^{2}-2\mu_{0}\sum_{i=1}^{n}X_{i}+n\mu_{0}^{2}\right]\\[0.7em]
&= \frac{1}{n}\left\{n(\sigma^{2}+\mu_{0}^{2})-2n\mu_{0}^{2}+n\mu_{0}^{2}\right\} = \sigma^{2}
\end{align}
特に,$E[X_{i}^{2}]$はカイ二乗分布を使うか悩むかもしれないが,$X_{i}$が従うのは標準正規分布ではなく正規分布であるため,$V[X]{=}E[X^{2}]{-}E[X]^{2}$を用いる方がよい。もしくは,$\sigma^{2}$の定義を用いてもよい。
母平均既知の$\N(\mu_{0},\sigma^{2})$に対し,$E[|X_{i}-\mu_{0}|]$を求める方法を説明せよ。
カイ二乗分布を用いれば絶対値を綺麗に外すことができる。$Y_{i}{=}(X_{i}-\mu_{0})^{2}/\sigma^{2}$とおくと$Y_{i}$は$\chi^{2}(1)$に従うため,$E[|X_{i}-\mu_{0}|]{=}E[\sigma\sqrt{Y_{i}}]$を計算することができる。カイ二乗分布は$\sqrt{X}$の計算も得意であることも意識しておくとよい。
母分散既知の正規母集団$\N(\mu,\sigma_{0}^{2})$からの標本平均$\barX$は$\mu$の有効推定量か。
対数尤度関数の二階微分は
\frac{\partial^{2}}{\partial \mu^{2}}\log f(x;\mu)
&= \frac{\partial^{2}}{\partial \mu^{2}} \left(-\frac{(x-\mu)^{2}}{2\sigma_{0}^{2}}+C\right)
= \frac{-1}{\sigma_{0}^{2}}
\end{align}
となる。ただし,$C$は$\mu$に依存しない定数を表す。したがって,クラメールラオの不等式における右辺は
\frac{1}{-nE[-1/\sigma_{0}^{2}]} &= \frac{\sigma_{0}^{2}}{n}
\end{align}
となる。一方,クラメールラオの不等式の左辺について$V[\barX]{=}\sigma_{0}^{2}/n$であるため,$\barX$はクラメールラオの不等式の下限を達成している。したがって,$\barX$は$\mu$の有効推定量である。
母分散未知の正規母集団$\N(\mu,\sigma^{2})$からの標本平均$\barX$は$\mu$の有効推定量か。
$\barX$は母分散が既知であれ未知であれ不偏推定量となる。したがって,前問と同様にして$\barX$が$\mu$の有効推定量であることを示せる。
母平均既知の正規母集団$\N(\mu_{0},\sigma^{2})$からの標本分散$S^{2}$は$\sigma^{2}$の有効推定量か。
$\sigma^{2}=\theta$とおくと,対数尤度関数の二階微分は
\frac{\partial^{2}}{\partial \mu^{2}}\log f(x;\theta)
&= \frac{\partial^{2}}{\partial \theta^{2}} \left(-\frac{\theta}{2}-\frac{(x-\mu)^{2}}{2\theta}+C\right)
= -\frac{1}{2\theta^{2}}
\end{align}
となる。ただし,$C$は$\theta$に依存しない定数を表す。したがって,クラメールラオの不等式における右辺は
\frac{1}{-nE[-1/1/(2\theta^{2})]} &= \frac{2\theta^{2}}{n}
\end{align}
となる。一方,クラメールラオの不等式の左辺について,
V[S^{2}]
&= E[S^{4}]-E[S^{2}]^{2} \\[0.7em]
&= E\left[\left(\frac{1}{n}\sum_{i=1}^{n}(X_{i}-\mu_{0})^{2}\right)^{2}\right]-\sigma^{4}\\[0.7em]
&= \frac{1}{n^{2}}\left\{\sum_{i=1}^{n}(X_{i}-\mu_{0})^{4}+\sum_{i\neq j}(X_{i}-\mu_{0})^{2}(X_{j}-\mu_{0})^{2}\right\}-\sigma^{4}
\end{align}
となるが,標準正規分布のモーメント母関数の$4$階微分を用いることにより
E\left[\left(\frac{X-\mu_{0}}{\sigma}\right)^{4}\right]
= M^{(4)}(0)
= \left\{1+\frac{t^{2}}{2}+\frac{1}{2!}\left(\frac{t^{2}}{2}\right)^{2}+\cdots\right\}^{(4)}\Biggr|_{t=0}
= 3
\end{align}
であるため,
V[S^{2}]
&= \frac{1}{n^{2}}\left\{3n\sigma^{4}+n(n-1)\sigma^{4}\right\}-\sigma^{4}
= \frac{2\sigma^{4}}{n} = \frac{2\theta^{2}}{n}
\end{align}
となり,$\barX$はクラメールラオの不等式の下限を達成している。したがって,$S^{2}$は$\sigma^{2}$の有効推定量である。
母平均未知の正規母集団$\N(\mu,\sigma^{2})$からの不偏分散$U^{2}$は$\sigma^{2}$の有効推定量か。
前問と同様に$V[U^{2}]$を計算すると,
V[U^{2}] &= \frac{2}{n-1}\theta^{2} > \frac{2}{n}\theta^{2} = V[S^{2}]
\end{align}
となり,$U^{2}$はクラメールラオの不等式の下限を達成していないため,$U^{2}$は$\sigma^{2}$の有効推定量ではない。
二項母集団$\Bin(m,p)$からの標本平均$\barX$は母比率$p$の有効推定量か。
対数尤度関数の二階微分は
\frac{\partial^{2}}{\partial p^{2}}\log f(x;p)
&= \frac{\partial^{2}}{\partial p^{2}} \left(x\log p+(m-x)\log(1-p)+C\right)
= \frac{(2p-1)x-mp^{2}}{p^{2}(1-p)^{2}}
\end{align}
となる。ただし,$C$は$p$に依存しない定数を表す。したがって,クラメールラオの不等式における右辺は
\frac{1}{-nE[((2p-1)x-mp^{2})/(p^{2}(1-p)^{2})]} &= \frac{p(1-p)}{nm}
\end{align}
となる。一方,クラメールラオの不等式の左辺について$V[\barX]{=}mp(1-p)/n$であるため,$\barX$はクラメールラオの不等式の下限を達成していない。そもそも,$E[\barX]{=}mp$であるため,不偏推定量ではないため有効推定量の議論をするまでもない。代わりに,不偏推定量$\barX/m$を考えれば,クラメールラオの不等式の左辺について$V[\barX/m]{=}p(1-p)/(mn)$となるため,$\barX/m$はクラメールラオの不等式の下限を達成している。以上より,$\barX$は$p$の有効推定量ではないが,$\barX/m$は$p$の有効推定量である。
ポアソン母集団$\Po(\lambda)$からの標本平均$\barX$は母平均$\lambda$の有効推定量か。
対数尤度関数の二階微分は
\frac{\partial^{2}}{\partial \lambda^{2}}\log f(x;\lambda)
&= \frac{\partial^{2}}{\partial \lambda^{2}} \left(x\log \lambda-\lambda+C\right)
= \frac{-x}{\lambda^{2}}
\end{align}
となる。ただし,$C$は$\lambda$に依存しない定数を表す。したがって,クラメールラオの不等式における右辺は
\frac{1}{-nE[-x/\lambda^{2}]} &= \frac{\lambda}{n}
\end{align}
となる。一方,クラメールラオの不等式の左辺について$V[\barX]{=}\lambda/n$であるため,$\barX$はクラメールラオの不等式の下限を達成している。したがって,$\barX$は$\lambda$の有効推定量である。
有効性の比較とはどういうことか。
推定量$T_{1},T_{2}$に対し,$V[T_{1}]$と$V_{T_{2}}$の大小を比較して小さい方が有効であると結論すること。
一致推定量を示す問題の定石を述べよ。
チェビシェフの不等式
P(|X-E[X]|<\varepsilon)\geq 1-\frac{V[X]}{\varepsilon^{2}}
\end{align}
を利用して$P(|T-\theta|<\varepsilon)$を下から評価する。確率の上限は$1$であることから,はさみうちの原理より$1$に収束することがわかる。
標本平均$\barX$は母平均の一致推定量であることを示せ。
$E[\barX]{=}\mu$と$V[\barX]{=}\sigma^{2}/n$とチェビシェフの不等式より,
P(|\barX-\mu|<\varepsilon)\geq 1-\frac{\sigma^{2}}{n\varepsilon^{2}}~\rarr~1\quad(n\rarr\infty)
\end{align}
が得られる。確率の上限が$1$であることとはさみうちの原理より,$\barX$は$\mu$の一致推定量となる。
標本分散$S^{2}$は母分散の一致推定量であることを示せ。
$S^{2}$を変形すると,
S^{2} &= \frac{1}{n}\sum_{i=1}^{n}(X_{i}-\barX)^{2} = \frac{1}{n}\sum_{i=1}^{n}(X_{i}-\mu)^{2}-(\barX-\mu)^{2} = S_{0}^{2}-(\barX-\mu)^{2}
\end{align}
となる。一般に,事象$A,B,C$に対して「$A$かつ$B$ならば$C$」が成り立つときに,$P(C)\geq P(A)P(B)$となる。$|S_{0}^{2}-\sigma^{2}|<\varepsilon/2$かつ$|\barX-\mu|<\sqrt{\varepsilon/2}$ならば$|S^{2}-\sigma^{2}|<\varepsilon$が成り立つため,
P(|S^{2}-\sigma^{2}|)
&\geq P\left(|S_{0}^{2}-\sigma^{2}|<\varepsilon/2\right)P\left(|\barX-\mu|<\sqrt{\varepsilon/2}\right)
\end{align}
となる。ここで,前問より$V[S_{0}^{2}]{=}2\sigma^{4}/n$であること,および$V[\barX]{=}\sigma^{2}/n$に注意すると,チェビシェフの不等式より
P(|S^{2}-\sigma^{2}|)
&\geq \left(1-\frac{(2\sigma^{4}/n)}{(\varepsilon/2)^{2}}\right)\left(1-\frac{(\sigma^{2}/n)}{\left(\sqrt{\varepsilon/2}\right)^{2}}\right)~\rarr~1\quad(n\rarr\infty)
\end{align}
が得られる。確率の上限が$1$であることとはさみうちの原理より,$S^{2}$は$\sigma^{2}$の一致推定量となる。もしくは,大数の法則より$\lim\barX\rarr \mu$を利用することでも簡単に示すことができる。
S^{2}
&= \frac{1}{n}\sum_{i=1}^{n}(X_{i}-\barX)^{2}\\[0.7em]
&= \frac{1}{n}\left(\sum_{i=1}^{n}X_{i}^{2}-2\mu\sum_{i=1}^{n}X_{i}+n\mu^{2}\right)\\[0.7em]
&= \frac{1}{n}\left\{\sum_{i=1}^{n}(X_{i}-\mu)^{2}-2\mu\sum_{i=1}^{n}(X_{i}-\mu)+n\mu^{2}-2\mu\sum_{i=1}^{n}X_{i}+n\mu^{2}\right\} = \sigma^{2}
\end{align}
不偏分散は母分散の一致推定量であることを示せ。
$(n-1)U^{2}/\sigma^{2}$は$\chi^{2}(n-1)$に従うこと,および$\chi^{2}(n-1)$の分散が$2(n-1)$であることから,
V[U^{2}] &= \frac{\sigma^{4}}{(n-1)^{2}}2(n-1) = \frac{2\sigma^{4}}{n-1}
\end{align}
となる。不偏分散の性質$E[U^{2}]{=}\sigma^{2}$とチェビシェフの不等式より,
P(|U^{2}-\sigma^{2}|<\varepsilon)\geq 1-\frac{2\sigma^{4}}{(n-1)\varepsilon^{2}}~\rarr~1\quad(n\rarr\infty)
\end{align}
となる。確率の上限が$1$であることとはさみうちの原理より,$U^{2}$は$\sigma^{2}$の一致推定量となる。
$T{=}(\varphi(X_{1})+\cdots+\varphi(X_{n}))/n$は$\theta{=}E[\varphi(X)]$の一致推定量であることを示せ。
まず,$E[T]{=}E[\varphi(X)]$と$V[T]{=}V[\varphi(X)]/n${\leq}M/nである。ただし,$X_{1},\ldots,X_{n}$は独立であることを用いた。したがって,チェビシェフの不等式より
P(|T-E[\varphi(X)]|<\varepsilon)
\geq 1-\frac{V[\varphi(X)]}{\varepsilon^{2}}
\geq 1-\frac{M}{n\varepsilon^{2}}~\rarr~1\quad(n\rarr\infty)
\end{align}
が得られる。確率の上限が$1$であることとはさみうちの原理より,$T$は$E[\varphi(X)]$の一致推定量となる。
母平均既知の正規母集団$\N(\mu_{0},\sigma^{2})$からの標本分散$S^{2}$は母分散$\sigma^{2}$の一致推定量か。
前問において$\varphi(x){=}(x-\mu_{0})^{2}$とおけば,$T{=}S_{0}^{2}$が$E[\varphi(X)]{=}\sigma^{2}$の一致推定量となることが示される。
正規母集団$\N(\mu,\sigma^{2})$からの標本平均$\barX$は母平均$\mu$の十分推定量であるか。
$T{=}\barX$とおいて正規分布の同時確率密度関数を変形することにより,
\prod_{i=1}^{n}f(x_{i})
&= \frac{1}{(2\pi\sigma)^{n/2}}\exp\left(-\frac{\sum_{i=1}^{n}(x_{i}-\mu)^{2}}{2}\right)\\[0.7em]
&= \frac{1}{(2\pi\sigma)^{n/2}}
\exp\left(-\frac{\sum_{i=1}^{n}x_{i}^{2}-2\mu\sum_{i=1}^{n}x_{i}+\mu^{2}}{2}\right)\\[0.7em]
&= \left\{\exp\left(\frac{-2\mu\sum_{i=1}^{n}x_{i}+\mu^{2}}{2}\right)\right\}\left\{\frac{1}{(2\pi\sigma)^{n/2}}\exp\left(-\frac{\sum_{i=1}^{n}x_{i}^{2}}{2}\right)\right\}\\[0.7em]
&= g(t;\mu)h(x)
\end{align}
となるため,フィッシャー・ネイマンの分解定理より$T$は母平均$\mu$の十分統計量である。
ポアソン母集団$\Po(\lambda)$からの標本平均$\barX$は母平均$\lambda$の十分推定量であるか。
$T{=}\barX$とおいてポアソン分布の同時確率密度関数を変形することにより,
\prod_{i=1}^{n}\frac{\lambda^{x_{i}}}{x_{i}!}e^{-\lambda}
= \left\{\left(\lambda^{\sum_{i=1}^{n}x_{i}/n}\right)^{n}e^{-n\lambda}\right\}\left(\frac{1}{x_{1}!\cdots x_{n}!}\right)
= g(t;\lambda)h(x)
\end{align}
となるため,フィッシャー・ネイマンの分解定理より$T$は母平均$\lambda$の十分統計量である。
二項分布$\Bin(m,p)$の$p$の最尤推定量を求めよ。
対数尤度関数の一階微分は
\frac{\partial}{\partial p}\log\left\{\left(\prod_{i=1}^{n}{}_{m}C_{x_{i}}\right)p^{n\barx}(1-p)^{mn-n\barx}\right\}
&= \frac{n\barx}{p}-\frac{mn-n\barx}{1-p}
\end{align}
となる。ただし,$C$は$p$に依存しない定数を表す。これを$0$とする$\hat{p}$を求めると,$\barx/m$が求める最尤推定量となる。厳密には増減表から$f(p)$が$\hat{p}$で最大値をとることを示す必要がある。
$\U(a,b)$における$a,b$の最尤推定量を求めよ。
同時確率密度関数は$f{=}1/(b{-}a)^{2}$となるが,$f$を最大にするためには$b{-}a$を最小にすればよい。そもそも,
a\leq\min(x_{1},\ldots,x_{n}),\quad \max(x_{1},\ldots,x_{n})\leq b
\end{align}
となるため,$a$はとり得る値の中で最大値である$\min(x_{1},\ldots,x_{n})$,$b$はとり得る値の中で最小値である$\max(x_{1},\ldots,x_{n})$が最尤推定量となる。最尤推定量は標本から決定されることを実感できる問題だ。
超幾何分布の最尤推定量を求めさせる問題の例とその答えを答えよ。
池の中から$m$匹の魚をとり,印をつけて池に戻す。しばらくして$n$匹の魚をとったときに印をつけた魚が$k$匹いた場合,池の中にいる魚の数$N$を最尤推定する。離散型であるため,微分ではなく尤度比を求める。
\frac{L(N)}{L(N-1)}
&= \frac{{}_{m}C_{k}{}_{N-m}C_{n-k}}{{}_{N}C_{n}}\frac{{}_{N-1}C_{n}}{{}_{m}C_{k}{}_{N-1-m}C_{n-k}}\\[0.7em]
&= \frac{(N-m)(N-n)}{N(N-m-n+k)}
= \frac{N^{2}-(m+n)N+mn}{N^{2}-(m+n)N+kN}
\end{align}
分数を展開せず分母と分子を比較する点がポイントだ。$L(N{-}1){\leq}L(N)$ならば$N{\leq}mn/k$となるため,
\hat{N} &=
\begin{cases}
\displaystyle
\frac{mn}{k}-1,~\frac{mn}{k}&(mn/k\text{が整数の場合})\\[0.7em]
\displaystyle
\left[\frac{mn}{k}\right]&(mn/k\text{が整数でない場合})
\end{cases}
\end{align}
となる。ただし,$[x]$は$x$の整数部分を表す。
有限母集団の非復元抽出における$\sigma^{2}$の不偏推定量を求めよ。
復元抽出と同様に,$T{=}\sum_{i=1}^{n}(X_{i}-\barX)^{2}/(n-1)$としてみる。$E[X_{i}-\mu]{=}0$および$E[\barX-\mu]{=}0$に注意して期待値を計算すると,
E[T]
&= \frac{1}{n-1}\left\{E\left[\sum_{i=1}^{n}(X_{i}-\mu)^{2}\right]-E\left[(\barX-\mu)^{2}\right]\right\}\\[0.7em]
&= \frac{1}{n-1}\left\{\sum_{i=1}^{n}V[X_{i}]-nV[\barX]\right\}\\[0.7em]
&= \frac{1}{n-1}\left\{\sigma^{2}-n\frac{N-n}{N-1}\frac{\sigma^{2}}{n}\right\}
= \frac{N}{N-1}\sigma^{2}\\[0.7em]
\end{align}
となる。したがって,
T &= \frac{N-1}{N}\frac{1}{n-1}\sum_{i=1}^{n}(X_{i}-\barX)^{2}
\end{align}
とおくと$E[T]{=}\sigma^{2}$となり,$\sigma^{2}$の不偏推定量となる。復元抽出において標本分散を$n/(n-1)$倍すると不偏分散になる関係性と似ていて興味深い。
非復元抽出で$T{=}a_{1}X_{1}+{\cdots}+a_{n}X_{n}$が母平均$\mu$の不偏推定量となり分散が最小となる条件を述べよ。
まず,$E[T]{=}\mu$より$\sum_{i=1}^{n}a_{i}{=}1$となる。次に,復元抽出では$X_{1},\ldots,X_{n}$の独立性を用いて$V[X_{i}]$の和を考えられたが,非復元抽出では$X_{1},\ldots,X_{n}$が独立ではないため,
V[T]
&= E[(T-E[T])^{2}]\\[0.7em]
&= E\left[\left(\sum_{i=1}^{n}a_{i}(X_{i}-\mu)\right)^{2}\right]\\[0.7em]
&= \sum_{i=1}^{n}a_{i}^{2}E[(X_{i}-\mu)^{2}]+\sum_{i\neq j}a_{i}a_{j}E[(X_{i}-\mu)(X_{j}-\mu)]\\[0.7em]
&= \sigma^{2}\sum_{i=1}^{n}a_{i}^{2}-\frac{\sigma^{2}}{N-1}\sum_{i\neq j}a_{i}a_{j}\\[0.7em]
&= \sigma^{2}\sum_{i=1}^{n}a_{i}^{2}-\frac{\sigma^{2}}{N-1}\left(1-\sum_{i=1}^{n}a_{i}^{2}\right)
= \frac{N\sigma^{2}}{N-1}\sum_{i=1}^{n}a_{i}^{2}-\frac{\sigma^{2}}{N-1}
\end{align}
を得る。ただし,上でみたように$i\neq j$に対し$E[(X_{i}{-}\mu)(X_{j}{-}\mu)]{=}-\sigma^{2}/(N{-}1)$および$\sum_{i=1}^{n}a_{i}{=}1$の両辺を二乗して余事象を利用した。すると,上でみたようにシュワルツの不等式より$a_{1}{=}{\cdots}{=}a_{n}{=}1/n$のとき$V[T]$は最小となる。特に,$i\neq j$のときにシグマの中身が残り続けるために$n(n-1)$のような係数が出現しないことに注意されたい。
ラオ・ブラックウェルの定理を説明せよ。
任意の推定量$\delta(X)$と十分統計量$T$に対し,$\delta^{\ast}(T){=}E[\delta(X)|T]$とおくと,全ての$\theta$に対して
E_{\theta}[(\delta^{\ast}(T)-\theta)^{2}] &\leq E_{\theta}[(\delta(X)-\theta)^{2}]
\end{align}
が成り立つことである。これは,どんな推定量$\delta(X)$に対しても,それが$T$の関数でなければ,$T$を条件付けた統計量を考えた方が平均二乗誤差が改良されることを示している。
ラオ・ブラックウェルの定理の適用例を述べよ。
ベルヌーイ分布$f(\theta){=}\theta^{x}(1-\theta)^{1-x}$からの標本$X_{1},\ldots,X_{n}$を例とする。$E[X_{1}]{=}\theta$であることから,$X_{1}$は$\theta$の不偏推定量である。一方,ベルヌーイ分布の同時確率質量関数とフィッシャー・ネイマンの分解定理より直ちに分かる通り,$S{=}\sum_{i=1}^{n}X_{i}$は十分統計量となる。したがって,
P(X_{1}=1|S=s)
&= \frac{P\left(X_{1}=1,\sum_{i=1}^{n}X_{i}=s-1\right)}{P\left(\sum_{i=1}^{n}X_{i}=s\right)}\\[0.7em]
&= \frac{P\left(X_{1}=1,\sum_{i=2}^{n}X_{i}=s-1\right)}{P\left(\sum_{i=1}^{n}X_{i}=s\right)}\\[0.7em]
&= \frac{P(X_{1}=1)P\left(\sum_{i=2}^{n}X_{i}=s-1\right)}{P\left(\sum_{i=1}^{n}X_{i}=s\right)}\\[0.7em]
&= \frac{\theta {}_{n-1}C_{s-1}\theta^{s-1}(1-\theta)^{n-s}}{{}_{n}C_{s}\theta^{s}(1-\theta)^{n-s}}
= \frac{s}{n} = \barx
\end{align}
が得られ,$E[X_{1}|T]{=}1\cdot P(X_{1}{=}1|S{=}s)+0\cdot P(X_{1}{=}0|S{=}s){=}P(X_{1}{=}1|S{=}s)$に注意すると,ラオ・ブラックウェルの定理より標本平均$\barX$は$X_{1}$よりも平均二乗誤差を小さくできるような推定量であることが示された。
モーメント法を説明せよ。
平均まわりのモーメントの定義は下記の通りである。
\begin{cases}
\displaystyle
\mu_{1} = \int_{-\infty}^{\infty}xf(x;\theta)dx\\[0.7em]
\displaystyle
\mu_{k} = \int_{-\infty}^{\infty}(x-\mu_{1})^{k}f(x;\theta)dx
\end{cases}
\end{align}
左辺を標本値による推定量で表し,右辺を$\theta$の関数として捉えた連立方程式の解は,$j{=}1,\ldots,m$に対し
\theta_{j} &= g_{j}(\mu_{1},\ldots,\mu_{k})
\end{align}
となる。$\theta_{j}$はモーメント推定量とよばれ,$\theta_{j}$を求める方法をモーメント法という。
モーメント法の適用例を述べよ。
ベルヌーイ分布は$\mu_{1}{=}p$となるが,$\mu_{1}{=}\barX$と置き換えることにより,$p$のモーメント推定量は$\barX$となる。
正規分布は$\mu_{1}{=}\mu$および$\mu_{2}{=}\sigma^{2}$となるが,$\mu_{1}{=}\barX$および$\mu_{2}{=}S^{2}$と置き換えることにより,$\mu$のモーメント推定量は$\barX$となり,$\sigma^{2}$のモーメント推定量は$S^{2}$となる。ただし,$S^{2}$は標本分散を表す。
ガンマ分布は$\mu_{1}{=}n/\lambda$および$\mu_{2}{=}n/\lambda^{2}$となるが,$\mu_{1}{=}\barX$および$\mu_{2}{=}S^{2}$と置き換えることにより,$\lambda$のモーメント推定量は$\barX/S^{2}$となり,$n$のモーメント推定量は$\barX^{2}/S^{2}$となる。
線形推定量を説明せよ。
$X_{1},\ldots,X_{n}$の線形和で表される推定量のこと。
線形不偏推定量を説明せよ。
線形推定量のうち不偏性を満たす推定量のこと。
線形不偏推定量の例を二つ上げよ。
線形回帰モデルの係数が挙げられる。$Y_{i}{=}\beta X_{i}{+}\varepsilon_{i}$とおき,$E[\varepsilon_{i}]{=}0$と仮定する。ただし,$X_{i}$は確率的ではない固定された値を表し,$\varepsilon_{i}$は確率的な値を表している。最小二乗法に基づいて$\beta$を推定すると,
\frac{\partial}{\partial \beta}\left\{\sum_{i=1}^{n}(Y_{i}-\beta X_{i})^{2}\right\}
&= -2\sum_{i=1}^{n}(Y_{i}-\beta X_{i})X_{i} = 0
\end{align}
より,$\hat{\beta}{=}\sum_{i=1}^{n}X_{i}Y_{i}/\sum_{i=1}^{n}X_{i}^{2}$となる。$\varepsilon_{i}$に関する期待値を考えると,
E\left[\frac{\sum_{i=1}^{n}X_{i}Y_{i}}{\sum_{i=1}^{n}X_{i}^{2}}\right]
&= E\left[\frac{\sum_{i=1}^{n}X_{i}(\beta X_{i}+\varepsilon_{i})}{\sum_{i=1}^{n}X_{i}^{2}}\right]
= \beta + \frac{\sum_{i=1}^{n}X_{i}^{2}E[\varepsilon_{i}]}{\sum_{i=1}^{n}X_{i}^{2}} = \beta
\end{align}
となり,$\hat{\beta}$は線形不偏推定量となる。他にも,$\hat{\beta}{=}\sum_{ij}X_{i}Y_{j}/\sum_{ij}X_{i}X_{j}$とおくと,$E[\varepsilon_{i}]{=}0$に注意して
E\left[\frac{\sum_{i,j}X_{i}Y_{j}}{\sum_{i,j}X_{i}X_{j}}\right]
&{=} E\left[\frac{(X_{1}{+}{\ldots}{+}X_{n})(Y_{1}{+}{\ldots}{+}Y_{n})}{(X_{1}{+}{\ldots}{+}X_{n})^{2}}\right]
{=} \beta E\left[\frac{(X_{1}{+}{\ldots}{+}X_{n})^{2}}{(X_{1}{+}{\ldots}{+}X_{n})^{2}}\right]
= \beta
\end{align}
となるため,$\hat{\beta}$は線形不偏推定量となる。
BLUE(最良線形不偏推定量)を説明せよ。
線形不偏推定量のうち真の母数との平均二乗誤差,すなわち分散を最小にする推定量のことを指す。不偏推定量のうち有効性を満たす推定量が有効推定量とよばれていたことから,最良線形不偏推定量は有効推定量そのものともいえるだろう。線形不偏推定量が担保しているのは「真の値からの誤差は平均すると$0$となるようにバランスよく散らばっている」ことは担保しているが,その散らばりが大きさは担保できていない。これを数式的に表現したものが,真の母数と推定量との二乗誤差を変形したバイアス・バリアンス分解である。$b(\theta){=}E_{\theta}[\theta]-\theta$とおくと,
E_{\theta}[(\hat{\theta}-\theta)^{2}]
&= E_{\theta}[(\hat{\theta}-E_{\theta}[\hat{\theta}]+E_{\theta}[\hat{\theta}-\theta)^{2}]
= V[\hat{\theta}]+b(\theta)
\end{align}
$b(\theta){=}0$となる推定量が線形不偏推定量で,加えて$V_{\theta}[\theta]$も最小化する推定量が最良線形不偏推定量である。
BLUE(最良線形不偏推定量)の求め方と例を述べよ。
上で計算したようにクラメール・ラオの下限を達成しているかどうかを調べればよい。例も同様。
ガウス・マルコフの定理を説明せよ。
$Y_{i}{=}\beta X_{i}{+}\varepsilon_{i}$の誤差項$\varepsilon_{i}$について,不偏性・等分散性・無相関性を仮定した場合に,最小二乗推定量$\hat{\beta}$が最良線形不偏推定量となる。ただし,
- 不偏性: $E[\varepsilon_{i}]=0$
- 等分散性: $V[\varepsilon_{i}]=\sigma^{2}$
- 無相関性: $i\neq j$に対し$E[\varepsilon_{i}\varepsilon_{j}]=0$
を表している。特に,$\varepsilon_{1},\ldots,\varepsilon_{n}$は独立とは限らず,正規分布等に従うとも限らないため,仮定としては非常に弱いものであることに注意する。
UMVUE(一様最小分散不偏推定量)を説明し,BLUE(最良線形不偏推定量)との関係を述べよ。
最良線形不偏推定量を線形モデルに限らず,一般に拡張した概念が一様最小分散不偏推定量である。
デルタ法を説明せよ。
語弊を恐れずに言うならば,$E[X]{=}\mu$および$V[X]{=}\sigma^{2}$に対し$\mu$まわりのテイラー展開
g(X) &= g(\mu) + \frac{g^{\prime}(\mu)}{1!}(X-\mu) + \frac{g^{\prime\prime}(\mu)}{2!}(X-\mu)^{2}+\cdots
\end{align}
を考えることにより,
\begin{cases}
\displaystyle
E\left[g(X)\right] = g(\mu)+\frac{g^{\prime\prime}(\mu)}{2}\sigma^{2}\\[0.7em]
\displaystyle
V\left[g(X)\right] = g^{\prime}(\mu)^{2}\sigma^{2}
\end{cases}
\end{align}
となることである。つまり,$E[X]$と$V[X]$から$E[g(X)]$と$V[g(X)]$を近似する方法である。厳密には分布収束や確率収束という概念を用いる必要があるが,まずはテイラー展開として近似する方法をおさえるとよい。
デルタ法の適用例を述べよ。
$E[X]{=}\mu$および$V[X]{=}\sigma^{2}$のとき,$E[\sqrt{X}]$と$V[\sqrt{X}]$は
\begin{cases}
\displaystyle
E\left[\sqrt{X}\right] = \sqrt{\mu}-\frac{1}{8}\mu^{-3/2}\sigma^{2}\\[0.7em]
\displaystyle
V\left[\sqrt{X}\right] = \frac{1}{4}\mu^{-1}\sigma^{2}
\end{cases}
\end{align}
と近似され,$E[X^{2}]$と$V[X^{2}]$は
\begin{cases}
\displaystyle
E\left[X^{2}\right] = \mu^{2}+\sigma^{2}\\[0.7em]
\displaystyle
V\left[X^{2}\right] = 4\mu^{2}\sigma^{2}
\end{cases}
\end{align}
と近似され,$E[\log X]$と$V[\log X]$は
\begin{cases}
\displaystyle
E\left[\log X\right] = \log\mu-\frac{1}{2}\mu^{-2}\sigma^{2}\\[0.7em]
\displaystyle
V\left[\log X\right] = \mu^{-2}\sigma^{2}
\end{cases}
\end{align}
と近似される。同様に,標本分散$S^{2}$に対して$E[S^{2}]{=}\sigma^{2}$および$V[S^{2}]{=}2\sigma^{2}/(n-1)$のとき,$E[S]$を近似する。デルタ法において$g(x){=}\sqrt{x}$とおけばよく,$n$が十分大きいときには$n-1{\approx}n$となることに注意して
E[S]
&{=} g(E[S^{2}])+\frac{g^{\prime\prime}(E[S^{2}])}{2}V[S^{2}]
{=} \sigma - \frac{\sigma^{-3}}{8}\frac{2\sigma^{4}}{n-1}
{=} \sigma-\frac{\sigma}{4(n-1)}
\approx \sigma-\frac{\sigma}{4n}
\end{align}
と近似される。
AICの定義とその意味を説明せよ。
\mathrm{AIC} &= -2\sum_{i=1}^{n}\log f(X_{i};\hat{\theta}_{n})+2\dim(\theta)
\end{align}
と定義される。対数尤度の最大化だけではモデルは過学習してしまうため,AICではパラメータの次元数を用いた正則化項を考えている。正則化項の$\dim(\theta)$は,真の分布と事後分布(推定されたパラメータを代入した分布)のKLダイバージェンスを最小化することにより導出される。
推定量の効率と相対効率を説明せよ。
クラメールラオの下限$J_{n}(\theta)^{-1}$に対する不偏推定量$\hat{\theta}$の分散の比率
\frac{J_{n}(\theta)^{-1}}{V[\hat{\theta}]}
\end{align}
を効率という。同様に,不偏推定量$\hat{\theta}_{2}$の分散に対する不偏推定量$\hat{\theta}_{1}$の分散の比
\frac{V[\hat{\theta}_{2}]}{V[\hat{\theta}_{1}]}
\end{align}
を相対効率という。
最尤推定量の一致性・漸近正規性・漸近有効性を説明せよ。
- 一致性: 漸近正規性と漸近有効性が成り立つための必要条件
- 漸近正規性: $\sqrt{n}(\hat{\theta}_{n}-\theta)\xrightarrow{d}\N(0,J_{1}(\theta)^{-1})$
- 漸近有効性: $\lim_{n\rarr\infty}E[{\sqrt{n}(\hat{\theta}_{n}-\theta)}^{2}]=J_{1}(\theta)^{-1})$
ただし,$\xrightarrow{d}$は分布収束を表している。漸近正規性は,$n$が十分大きいときに$\sqrt{n}(\hat{\theta}_{n}-\theta)$の極限分布が正規分布となり,極限分布の分散はクラメールラオの下限を達成していることを表している。漸近有効性は,$n$が十分大きいときに$V[{\sqrt{n}(\hat{\theta}_{n}-\theta)}]$が極限分布の分散と等しくなること,すなわち最尤推定量の分散の極限がクラメールラオの下限を達成していることを表している。
ポイント集
覚えた方が楽になるポイント
多変量正規分布の変数変換
AX+b &\sim \N(A\mu+b,A\Sigma A^{T})
\end{align}
モーメント母関数を変形することにより証明できる。
多変量正規分布の標準化
Z &= \Sigma^{-1/2}(X-\mu)
\end{align}
上で述べた多変量正規分布の変数変換を利用することで証明できる。
多変量正規分布の独立性
$D$次元多変量正規分布$X{\sim}\N(\mu,\Sigma)$において,$X_{1}{\in}\mR^{D_{1}}$と$X_{2}{\in}\mR^{D-D_{1}}$が独立となる必要十分条件は,$\Sigma_{12}{=}O_{D_{1},N-D_{1}}$である。モーメント母関数の一意性より,$M_{X}(t){=}M_{X_{1}}(t)M_{X_{2}}(t)$の恒等式を変形していくことで証明できる。
多変量正規分布の条件付き確率
X_{1}|(X_{2}=x_{2}) &\sim \N(\mu_{1}+\Sigma_{12}\Sigma_{22}^{-1}(x_{2}-\mu_{2}),\Sigma_{11|2})
\end{align}
ただし,$\Sigma_{11|2}=\Sigma_{11}-\Sigma_{12}\Sigma_{22}^{-1}\Sigma_{21}$とおいた。証明は天下り的な行列を与える必要があるため覚えなくてもよい。
偏相関係数
\rho(X,Y|Z) &= \frac{\rho(X,Y)-\rho(X,Z)\rho(Y,Z)}{\sqrt{1-\rho(X,Z)^{2}}\sqrt{1-\rho(Y,Z)^{2}}}
\end{align}
チェビシェフの不等式
任意の確率変数$X$と$\varepsilon>0$に対し,
\begin{cases}
\displaystyle
P\left( \left| X - E[X] \right| \geq \varepsilon \right) \leq \frac{V[X]}{\varepsilon^2}\\[0.7em]
\displaystyle
P\left( \left| X - E[X] \right| \leq \varepsilon \right) \geq 1-\frac{V[X]}{\varepsilon^2}
\end{cases}
\end{align}
大数の弱法則
P\left( \left| \frac{1}{n} \sum_{i=1}^nX_i - \mu\right| \geq \varepsilon \right) \rightarrow 0 \quad (n\rightarrow \infty)
\end{align}
中心極限定理
P\left( \frac{1}{\sqrt{n}}\sum_{i=1}^n \frac{X_i - \mu}{\sqrt{\sigma^2}}\leq x \right)
\rightarrow \int_{-\infty}^{x}\frac{1}{2\pi}e^{-t^{2}/2}dt\quad (n \rightarrow \infty)
\end{align}
大数の弱法則/大数の強法則/中心極限定理の違い
- 大数の弱法則: 算術平均が母平均に確率収束すること
- 大数の強法則: 算術平均が母平均に概収束すること
- 中心極限定理: 算術平均と母平均の差は$\N(0,\sigma^{2}/n)$に分布収束すること
覚えておくと差がつくポイント
条件付き期待値と条件付き分散の性質
\begin{cases}
E_{X}[X] = E_{Y}[E_{X}[X|Y]]\\[0.7em]
V_{X}[X] = E_{Y}[V_{X}[X|Y]]+V_{Y}[E_{X}[X|Y]]
\end{cases}
\end{align}
条件付き期待値は「$Y$で条件付けたなら$Y$の期待値をとりなさい」と覚え,条件付き分散は「$Y$で条件付けた分散の期待値と期待値の分散の和」と覚えてしまう。
共分散の性質
&\Cov [aX_{1}+bY_{1}, cX_{2}+dY_{2}]\notag\\[0.7em]
&\quad\quad= ac\Cov[X_{1}, Y_{1}] + ad\Cov[X_{1}, Y_{2}] + bc\Cov[X_{2}, Y_{1}] + bd\Cov[X_{2}, Y_{2}]
\end{align}
標本分散の分散と不偏分散の分散
\begin{cases}
\displaystyle
V[S^{2}] = \frac{(n-1)^{2}}{n^{3}}\left\{\mu_{4}-\frac{n-3}{n-1}\sigma^{4}\right\}\\[0.7em]
\displaystyle
V[U^{2}] = \frac{1}{n}\left\{\mu_{4}-\frac{n-3}{n-1}\sigma^{4}\right\}
\end{cases}
\end{align}
ひっかけポイント
- 確率変数の定義域は必ず確認して解答にも明示する
- 特に$0$となる区間も明記する
- 満点を逃すとしたら定義域まわりである
- 変数変換した際の逆変換から求められる定義域上で積分する
- 四則演算による変数変換では共通部分を考える区間の幅に注意する
- $(X,Y)\rarr U$は片方の区間が定数になるが$(X,Y)\rarr (U,V)$は両方変数となるため図示する
- 凡ミスしない
- $G^{\prime}(1){=}E[X]$と$G^{\prime\prime}(1){=}E[X(X-1)]$
- $M^{\prime}(0){=}E[X]$と$M^{\prime\prime}(0){=}E[X^{2}]$
- $g(x)$の期待値を計算しているのに被積分関数に$g(x)$を掛け忘れて全確率を計算しない
- 順序統計量の具体的な例の計算で$n,k,i$を残したままにしない
- 一変数の場合にヤコビアンに絶対値を適用し忘れない
- $x$を積分して$x$のままにしない
- $(x_{1}+\cdots+x_{n})^{2}=x_{1}^{2}+\cdots+x_{n}^{2}$としない
- 最尤推定で$n$個の同時確率関数ではなく$1$個の確率関数を考えない
参考文献
本稿の執筆にあたり参考にした文献は,以下でリストアップしております。

コメント
コメント一覧 (2件)
素敵なTips集ありがとうございます。本番前にzukaさんのサイトを見つける事ができて幸運でした。残り1ヶ月ほど、こちらのサイトを参考にしながら頑張りたいと思います。
嬉しいコメントありがとうございます。ご質問・ご指摘があればコメント下さいませ。