本記事は数学の徹底解説シリーズに含まれます。
初学者の分かりやすさを優先するため,多少正確でない表現が混在することがあります。もし致命的な間違いがあればご指摘いただけると助かります。
線型変換の積の次元と次元の和
$G_{1},\ldots,G_{s}$を$n$次元ベクトル空間$V$の線型変換とし,それらの積を$G=G_{1}\cdots G_{s}$とすれば,
\dim (\Ker G) &\leq \sum_{i=1}^{s}\dim (\Ker G_{i})\label{主題}
\end{align}
が成り立つ。
分解定理の証明に利用される定理です。
証明
$s$に関する帰納法を利用します。$s{=}1$のときは,明らかに式($\ref{主題}$)は成り立ちます。いま,$G_{1},\ldots,G_{s-1}$に対して式($\ref{主題}$)が成り立つと仮定します。以下では,$G_{1},\ldots,G_{s}$に対して式($\ref{主題}$)が成り立つことを示します。
簡単のため,$H{=}G_{1}\cdots G_{s-1}$とおきます。$\Im G_{s}{=}V^{\prime}$とし,$H$の定義域を$V^{\prime}$に縮小した$V^{\prime}$から$V$への線型写像を$H^{\prime}$とします。このとき,$G_{s},H,H^{\prime}$を次元定理に基づき可視化すると,
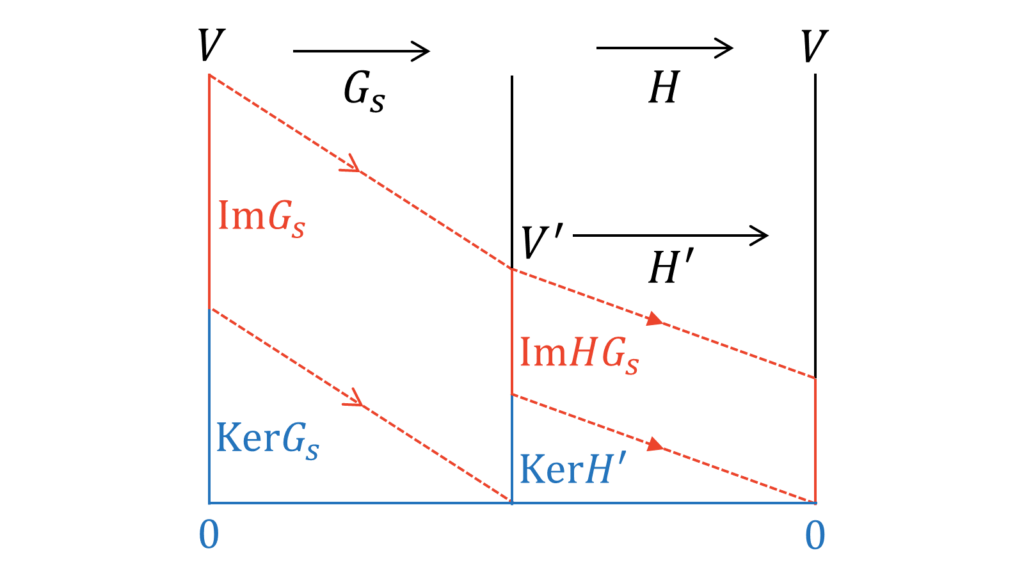
となります。上図より,
\dim (\Im G_{s})-\dim(\Im HG_{s}) &= \dim(\Ker H^{\prime})\label{1}\\[0.7em]
n-\dim(\Ker G_{s}) &= \dim(\Im G_{s})\label{2}
\end{align}
が成り立ちます。また,上図を抽象化すると,
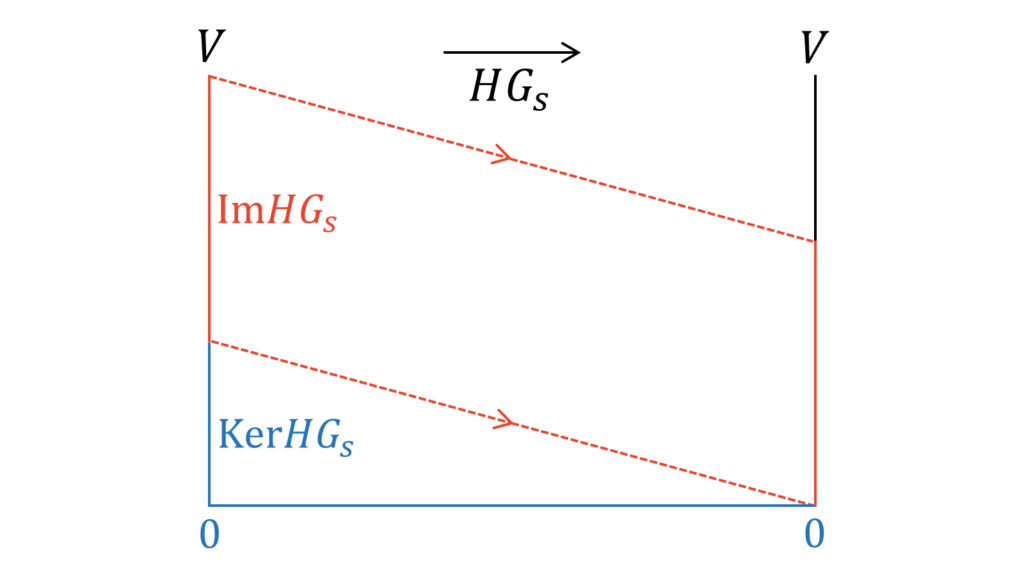
となります。上図より,
\dim(\Im HG_{s}) &= n-\dim (\Ker HG_{s})\label{3}
\end{align}
が成り立ちます。式($\ref{2}$)と式($\ref{3}$)を式($\ref{1}$)に代入すると,
\dim(\Ker HG_{s})-\dim(\Ker G_{s}) &= \dim(\Ker H^{\prime})\label{4}
\end{align}
が得られます。ここで,$H^{\prime}$の定義より
\Ker H^{\prime} &= V^{\prime} \cap \Ker H &&\subset \Ker H
\end{alignat}
となりますので,次元を考えると
\dim(\Ker H^{\prime}) \leq \dim(\Ker H)\label{5}
\end{align}
が成り立ちます。式($\ref{5}$)を式($\ref{4}$)に代入すると,
\dim(\Ker HG_{s})-\dim(\Ker G_{s}) &\leq \dim(\Ker H)
\end{align}
が得られます。すなわち,帰納法の仮定を利用すると,
\dim(\Ker HG_{s}) &= \dim (\Ker G)\\[0.7em]
&\leq \dim(\Ker H)+\dim(\Ker G_{s}) \\[0.7em]
&\leq \sum_{i=1}^{s-1}\dim (\Ker G_{i})+\dim(\Ker G_{s})\\[0.7em]
&= \sum_{i=1}^{s}\dim (\Ker G_{i})
\end{align}
が得られます。したがって,$G_{1},\ldots,G_{s}$に対して式($\ref{主題}$)が成り立つことが示され,帰納法により上の主張の証明が完了しました。


コメント