統計検定1級の過去問解答解説を行います。目次は以下をご覧ください。
不適切な内容があれば，記事下のコメント欄またはお問い合わせフォームよりご連絡下さい。
問題
統計検定1級の過去問からの出題になります。統計検定の問題の著作権は日本統計学会に帰属していますので，本稿にて記載することはできません。「演習問題を俯瞰する」で詳しく紹介している公式の過去問題集をご購入いただきますようお願い致します。
解答
カイ二乗分布と逆関数法に関する出題でした。
(1)
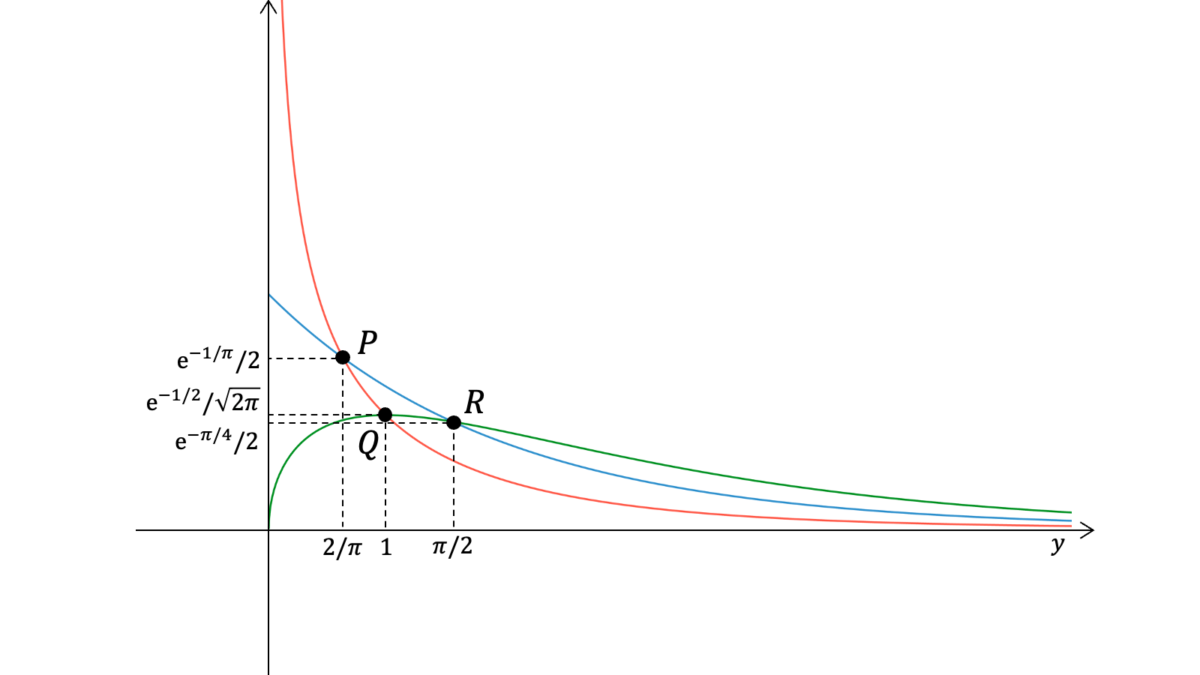
$f_{1}(y)$，$f_{2}(y)$，$f_{3}(y)$のグラフは下記の通りである。ただし，$f_{1}$と$f_{2}$の交点を$P$，$f_{2}$と$f_{3}$の交点を$Q$，$f_{1}$と$f_{3}$の交点を$R$とおいた。
まず，$f_{k}(y)$の定義より$f_{1}(y)$，$f_{2}(y)$，$f_{3}(y)$の確率密度関数を求めておきます。
\begin{cases}
\displaystyle
f_{1}(y)=\frac{1}{\sqrt{2\pi}}\frac{e^{-y/2}}{\sqrt{y}}\\[0.7em]
\displaystyle
f_{2}(y)=\frac{1}{2}e^{-y/2}\\[0.7em]
\displaystyle
f_{3}(y)=\frac{1}{\sqrt{2\pi}}\sqrt{y}e^{-y/2}
\end{cases}
\end{align}
$f_{1}$の形は単調減少関数$y^{-1/2}$と単調減少関数$e^{-y/2}$の積であるため単調減少関数であり，$f_{2}$の形は単調減少関数$e^{-y/2}$となります。一方，$f_{3}$の導関数が$0$となる$\hat{y}$は
\frac{df_{3}}{dy}
&= \frac{1}{\sqrt{2\pi}}\left\{\frac{1}{2}y^{-1/2}e^{-y/2}-\frac{1}{2}y^{1/2}e^{-y/2}\right\}
= -\frac{y^{-1/2}e^{-y/2}(y-1)}{2\sqrt{2\pi}}
\end{align}
を満たすため，$\hat{y}{=}1$となります。$f_{1}{=}f_{2}$を変形すると$\sqrt{2\pi y}{=}2$，$f_{1}{=}f_{3}$を変形すると$y{=}1$，$f_{2}{=}f_{3}$を変形すると$2\sqrt{y}{=}\sqrt{2\pi}$となるため，$f_{1}$と$f_{2}$の交点$P$，$f_{2}$と$f_{3}$の交点$Q$，$f_{1}$と$f_{3}$の交点$R$はそれぞれ
P = \left(\frac{2}{\pi},\frac{e^{-1/\pi}}{2}\right),\quad
Q = \left(1,\frac{e^{-1/2}}{\sqrt{2\pi}}\right),\quad
R = \left(\frac{\pi}{2},\frac{e^{-\pi/4}}{2}\right)
\end{align}
となります。以上より，下記のような増減表を書くことができます。
| $y$ | $+0$ | $\cdots$ | $2/\pi$ | $\cdots$ | $1$ | $\cdots$ | $\pi/2$ | $\cdots$ | $+\infty$ |
|---|---|---|---|---|---|---|---|---|---|
| $f_{1}$ | $+\infty$ | $\cdots$ | $e^{-1/\pi}/2$ | $\cdots$ | $e^{-1/2}/\sqrt{2\pi}$ | $\cdots$ | $\searrow$ | $\cdots$ | $0$ |
| $f_{2}$ | $1/2$ | $\cdots$ | $e^{-1/\pi}/2$ | $\cdots$ | $\searrow$ | $\cdots$ | $e^{-\pi/4}/2$ | $\cdots$ | $0$ |
| $f_{3}$ | $0$ | $\cdots$ | $\nearrow$ | $\cdots$ | $e^{-1/2}/\sqrt{2\pi}$ | $\cdots$ | $e^{-\pi/4}/2$ | $\cdots$ | $0$ |
| 備考 | - | - | $f_{1}{=}f_{2}{>}f_{3}$ | - | $f_{2}{>}f_{1}{=}f_{3}$かつ$f_{3}$は極値 | - | $f_{2}{=}f_{3}{>}f_{1}$ | - | - |
したがって，$f_{1}(y)$，$f_{2}(y)$，$f_{3}(y)$のグラフは下記のようになります。
$y^{-1/2}$に$y{=}0$を代入して$0$と早とちりしないようにしてください。$y$の逆数に$0$を代入するため，正の無限大に発散します。分数表記ではなく$y^{-1/2}$と分数表記して計算すると凡ミスしやすいため注意が必要です。
(2)
与えられた変数変換に$W=Y_{1}$を加えて考える。逆変換は
\begin{cases}
\displaystyle
Z = X\sqrt{W}\\[0.7em]
Y_{1} = W
\end{cases}
\end{align}
となるため，ヤコビアンは
J &=
\begin{vmatrix}
\partial x\sqrt{w}/\partial x & \partial x\sqrt{w}/\partial w\\[0.7em]
\partial w/\partial x & \partial w/\partial w
\end{vmatrix}
=
\begin{vmatrix}
\sqrt{w} & xw^{-1/2}/2\\[0.7em]
0 & 1
\end{vmatrix} = \sqrt{w}
\end{align}
となる。したがって，$f_{k}$と$\varphi$が独立であることから，
g(x)
&= \int_{0}^{\infty}f_{k}(w)\varphi(x\sqrt{w})(\sqrt{w}dw)\\[0.7em]
&= \int_{0}^{\infty}\frac{1}{\sqrt{2\pi}}w^{-1/2}e^{-w/2}\cdot \frac{1}{\sqrt{2\pi}}e^{-x^{2}w}(\sqrt{w}dw)\\[0.7em]
&= \frac{1}{2\pi}\int_{0}^{\infty}e^{-(1+x^{2})w/2}dw\\[0.7em]
&= \frac{1}{2\pi}\left[-\frac{2}{1+x^{2}}e^{-(1+x^{2})w/2}\right]_{0}^{\infty}
= \frac{1}{\pi(1+x^{2})}
\end{align}
と求められる。
$g(x)$はコーシー分布の確率密度関数です。
(3)
$-\pi/2<w<\pi/2$に対し，
h(w) &= \frac{1}{\pi}
\end{align}
となる。この分布は区間$(-\pi/2,\pi/2)$上の一様分布である。
$W{=}\tan^{-1}X$より，$dx/dw{=}1{+}x^{2}$となります。逆変換が$-\pi/2{<}W{<}\pi/2$に対し$X{=}\tan W$となるため，
h(w) &= g(x)\frac{dx}{dw} = \frac{1}{\pi(1+x^{2})}(1+x^{2}) = \frac{1}{\pi}
\end{align}
が得られます。ただし，$(\tan^{-1}x)^{\prime}=1/(1+x^{2})$を利用しました。
(4)
$i{=}1,2,\ldots$に対し，
X_{i} &= \tan\left(\pi U_{i}-\frac{\pi}{2}\right)\label{4-1}
\end{align}
のように$X_{i}$を定めることにより，小問(2)の分布に従う$X_{i}$を生成できる。
一様乱数から逆関数を用いて特定の分布に従う確率変数を生成することを，逆関数法とよびます。
小問(3)より，区間$(-\pi/2,\pi/2)$上の一様分布に従う$W$を用いることで，小問(2)の分布に従う$X$が生成できることが分かりました。本問では，区間$(0,1)$上の一様分布に従う$U$から$X$を生成することが目的です。
ところで，$W$が従う区間$(-\pi/2,\pi/2)$上の一様分布は，区間$(0,1)$上の一様分布に従う$U$を変数変換することによって得られます。具体的には，区間$(-\pi/2,\pi/2)$の長さは区間$(0,1)$の長さの$\pi$倍であるため，$W{=}\pi U$を考えます。これだけでは$W$は区間$(0,\pi)$上の一様分布に従うため，$-\pi/2$だけ並行移動した$W{=}\pi U{-}\pi/2$を考えれば，$W$は区間$(-\pi/2,\pi/2)$上の一様分布に従うことが分かります。したがって，小問(3)より式($\ref{4-1}$)のように$X$を定めれば，小問(2)の分布に従う$X$が生成できることが示されました。
コメント