統計検定1級の過去問解答解説を行います。目次は以下をご覧ください。
不適切な内容があれば,記事下のコメント欄またはお問い合わせフォームよりご連絡下さい。
問題
統計検定1級の過去問からの出題になります。統計検定の問題の著作権は日本統計学会に帰属していますので,本稿にて記載することはできません。「演習問題を俯瞰する」で詳しく紹介している公式の過去問題集をご購入いただきますようお願い致します。
解答
ラプラス分布とベイズ推定に関する出題でした。
(1)
ラプラス分布のモーメント母関数は
M(t)
&= \int_{-\infty}^{\infty}\frac{\lambda}{2}e^{t\mu-\lambda|\mu-\xi|}d\lambda\\[0.7em]
&= \int_{-\infty}^{\infty}\frac{\lambda}{2}e^{t(x/\lambda+\xi)-|x|}\frac{dx}{\lambda}\\[0.7em]
&= \frac{e^{t\xi}}{2}\int_{-\infty}^{\infty}e^{tx/\lambda-|x|}dx\\[0.7em]
&= \frac{e^{t\xi}}{2}\int_{-\infty}^{0}e^{(t+\lambda)x/\lambda}dx+\frac{e^{t\xi}}{2}\int_{0}^{\infty}e^{(t-\lambda)x/\lambda}dx\\[0.7em]
&= \frac{e^{t\xi}}{2}\left(\frac{\lambda}{t+\lambda}-\frac{\lambda}{t-\lambda}\right)
= \frac{\lambda^{2}}{\lambda^{2}-t^{2}}e^{t\xi}
\end{align}
となる。$M(0){=}1$に注意すると,原点周りの一次モーメントは
M^{\prime}(0)
&= \left\{\frac{\lambda^{2}\xi e^{t\xi}(\lambda^{2}-t^{2})-2\lambda^{2}e^{t\xi}t}{(t^{2}-\lambda^{2})^{2}}\right\}\Biggr|_{t=0}\\[0.7em]
&= \left\{\xi M(t)+2M(t)\frac{t}{\lambda^{2}-t^{2}}\right\}\Biggr|_{t=0}\\[0.7em]
&= \xi
\end{align}
と表され,原点周りの二次モーメントは
M^{\prime\prime}(0)
&= \left\{\xi M^{\prime}(t)+2M^\prime(t)\frac{t}{\lambda^{2}-t^{2}}+2M^\prime(t)\frac{(\lambda^{2}-t^{2})+2t^{2}}{(\lambda^{2}-t^{2})^{2}}\right\}\Biggr|_{t=0}\\[0.7em]
&= \xi^{2}+\frac{2}{\lambda^{2}}
\end{align}
と表される。以上より,分散は
V[\mu] &= E[X^{2}]-E[X]^{2} = \left(\xi^{2}+\frac{2}{\lambda^{2}}\right)-\xi^{2} = \frac{2}{\lambda^{2}}
\end{align}
と表される。
平均と分散の定義から計算してもよいですが,モーメント母関数を利用した方が少し計算が楽になります。
(2)
g(\mu|\vy) &= \frac{\lambda}{2(2\pi)^{n/2}}\exp\left\{-\frac{1}{2}\sum_{i=1}^{n}(y_{i}-\bary)^{2}-\frac{n}{2}(\mu-\bary)^{2}-\lambda|\mu-\xi|\right\}
\end{align}
$\vy$の同時確率密度関数は
g(\vy|\mu)
&= \prod_{i=1}^{N}\frac{1}{\sqrt{2\pi}}\exp\left\{-\frac{(y_{i}-\mu)^{2}}{2}\right\}
= \frac{1}{(2\pi)^{n/2}}\exp\left\{-\frac{1}{2}\sum_{i=1}^{n}(y_{i}-\mu)^{2}\right\}
\end{align}
となりますので,条件付き確率の定義より
g(\mu|\vy)
&\propto g(\vy|\mu)g(\mu)\\[0.7em]
&= \frac{1}{(2\pi)^{n/2}}\exp\left\{-\frac{1}{2}\sum_{i=1}^{n}(y_{i}-\mu)^{2}\right\}\cdot\frac{\lambda}{2}e^{-\lambda|\mu-\xi|}\\[0.7em]
&= \frac{\lambda}{2(2\pi)^{n/2}}\exp\left\{-\frac{1}{2}\sum_{i=1}^{n}(y_{i}-\mu)^{2}-\lambda|\mu-\xi|\right\}\\[0.7em]
&= \frac{\lambda}{2(2\pi)^{n/2}}\exp\left[-\frac{1}{2}\sum_{i=1}^{n}\left\{(y_{i}-\bary)-(\mu-\bary)\right\}^{2}-\lambda|\mu-\xi|\right]\\[0.7em]
&= \frac{\lambda}{2(2\pi)^{n/2}}\exp\left\{-\frac{1}{2}\sum_{i=1}^{n}(y_{i}-\bary)^{2}-\frac{n}{2}(\mu-\bary)^{2}-\lambda|\mu-\xi|\right\}\\[0.7em]
\end{align}
と求められます。ただし,後の問題のために$\bary$を用いて変形を進めておきました。
この$\bary$を用いた式変形は不偏分散や正規分布のモーメントの計算時によく利用される方法です。
(3)
\hat{\mu} &=
\begin{cases}
\displaystyle
\max\left(\xi,~\bary-\frac{\lambda}{n}\right)&(\bary>\xi)\\[0.7em]
\displaystyle
\xi&(\bary=\xi)\\[0.7em]
\displaystyle
\min\left(\xi,~\bary+\frac{\lambda}{n}\right)&(\bary<\xi)\\[0.7em]
\end{cases}
\end{align}
対数事後確率の$\mu$に関する項目を$L$とおくと,
\log(\mu|\vy) \propto -\frac{n}{2}(\mu-\bary)^{2}-\lambda|\mu-\xi| \equiv L
\end{align}
となります。したがって,$\mu-\xi>0$のとき,
\frac{\partial L}{\partial \mu} &= -n(\mu-\bary)-\lambda = 0
\end{align}
が得られます。したがって,$\hat{\mu}{=}\max(\xi,\bary-\lambda/n)$となります。同様に$\mu-\xi< 0$のとき,$L$を$\mu$で偏微分して$0$とおくと,
\frac{\partial L}{\partial \mu} &= -n(\mu-\bary)+\lambda = 0
\end{align}
が得られます。したがって,$\hat{\mu}=\min(\xi,\bary+\lambda/n)$となります。$\mu-\xi=0$のとき,$L$は上に凸の二次関数となるため,$\hat{\mu}=\bary$となります。ここで,$\hat{\mu}$の値が未知母数$\mu$によって場合分けされているため,$\bary$を用いて条件を変換します。やや技巧的ですが,
L &= -\frac{n}{2}\left\{(\mu-\xi)-(\bary-\xi)\right\}^{2}-\lambda|\mu-\xi|
\end{align}
と変形します。本質的には小問(2)と同様の式変形になります。$L$を最大化するために,$\mu-\xi$と$\bary-\xi$の符号に着目しましょう。第二項目の符号が常に一定であることを踏まえると,第一項目の二乗の中身が最小化となるときは,$\mu-\xi$と$\bary-\xi$の符号は同符号となることが分かります。つまり場合分けの条件式においては$\mu$を$\bary$とおけばよく,求める答えは上の解答のようになります。
(4)
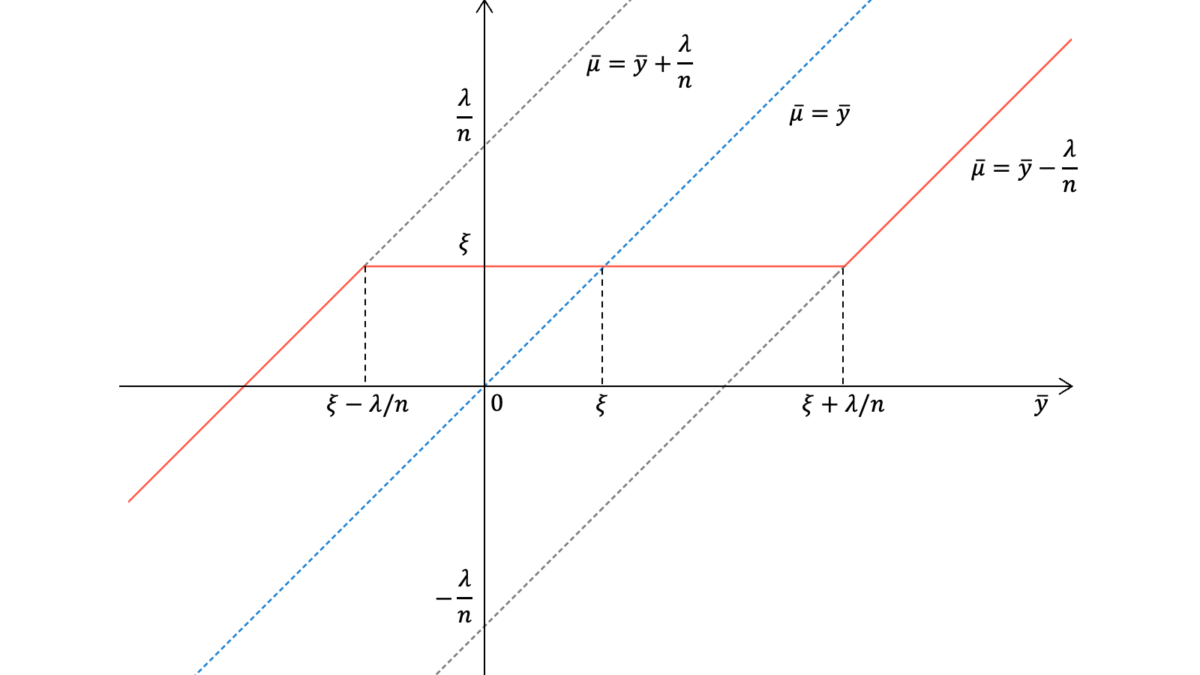
上図の赤線がベイズ推定による推定値であり,青点線が最尤推定による推定値である。$\bary$が$\xi$に近い値を取る場合は,ベイズ推定値と最尤推定値も近い値を取る。逆に,$\bary$が$\xi$から極端に小さな値を取る場合はベイズ推定値は最尤推定値よりも大きいな推定値となり,$\bary$が$\xi$から極端に大きな値を取る場合はベイズ推定値は最尤推定値よりも小さいな推定値となる。これは,ベイズ推定における事前分布が極端な推定値となることを防ぐ正則化の役割を果たすことを示唆している。
ベイズ推定における事前分布は,最尤推定と比較した際には標本値への過学習を防ぐための正則化の役割を果たします。なお,上の解答では本番で使うことのできない「赤線」や「青線」という言葉を使っていますが,これは分かりやすさを優先したためであり,実際の試験ではベイズ推定値の点線を削除し,実線と点線で区別するとよいでしょう。


コメント