本記事は数学の徹底解説シリーズに含まれます。
初学者の分かりやすさを優先するため,多少正確でない表現が混在することがあります。もし致命的な間違いがあればご指摘いただけると助かります。
目次
行列の符号と行と列の入れ替え
行列$A\in M_{n}(\mK)$に対し,$k$行目と$l$行目,$k$列目と$l$列目を入れかえた行列を$\hat{A}$とおく。ただし,$\mK$は複素数空間$\mC$または実数空間$\mR$を表し,$M_{n}(\mK)$は$\mK$上の$n$次正方行列全体の集合とする。このとき,$A$の符号と$\hat{A}$の符号は変わらない。
例えば$A$が正定値ならば$\hat{A}$も正定値になります。
証明
$n$次元内積空間の任意の元を$\vx=[x_{1},\ldots,x_{n}]^{T}$とおきます。双一次形式の行列による表現より,$x_{i}x_{j}$の係数は$a_{ij}+a_{ji}$となります。したがって,エルミート形式
\begin{align}
f(\vx,\vx) &= \overline{\vx}^{T}A\vx\label{エルミート形式}
\end{align}
f(\vx,\vx) &= \overline{\vx}^{T}A\vx\label{エルミート形式}
\end{align}
の符号は集合
\begin{align}
\left\{(a_{ij},a_{ji})\mid 1\leq i\leq n,~1\leq j\leq n\right\}\label{集合}
\end{align}
\left\{(a_{ij},a_{ji})\mid 1\leq i\leq n,~1\leq j\leq n\right\}\label{集合}
\end{align}
によって定まることが分かります。
$\vx$は$n$次元内積空間の元を動き回るので,式($\ref{エルミート形式}$)の符号を定めるのは係数となります。
いま,$A$と$\hat{A}$を比べると,下図の通りある$(a_{kj},a_{jk})$のペアは$(\hat{a}_{lj},\hat{a}_{jl})$ペアに飛ばされます。
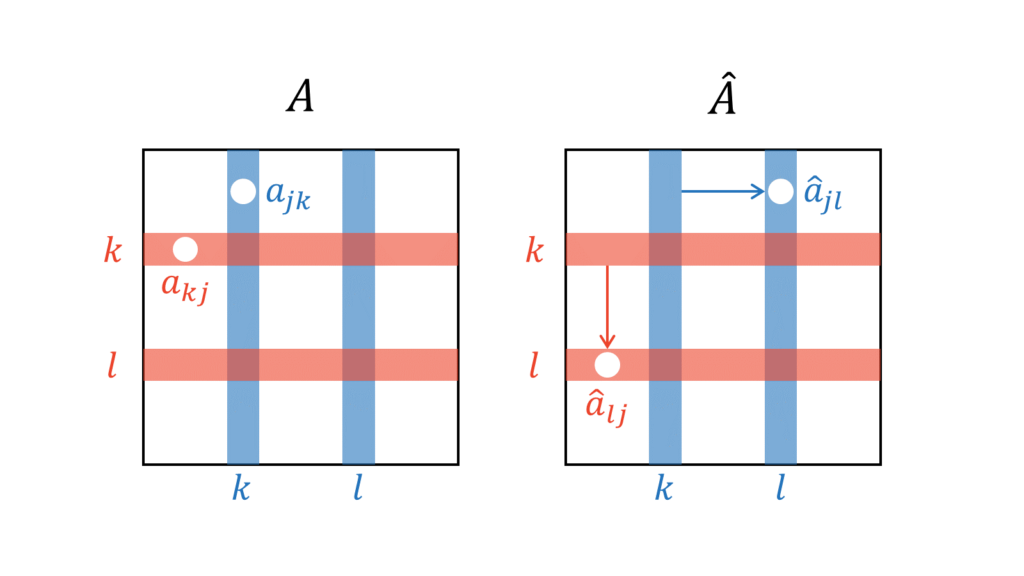
同様に,$(a_{lj},a_{jl})$のペアは$(\hat{a}_{kj},\hat{a}_{jk})$ペアに飛ばされますので,集合($\ref{集合}$)は$A$と$\hat{A}$で変わらないことが分かります。したがって,$A$の符号と$\hat{A}$の符号は変わらないことが示されました。


コメント