本記事は「これなら分かる!はじめての数理統計学」シリーズに含まれます。
不適切な内容があれば,記事下のコメント欄またはお問い合わせフォームよりご連絡下さい。
超幾何分布
f_{X}(x) &= \frac{{}_M \tilde{\C}_{x} \times {}_{N-M} \tilde{\C}_{n-x}}{{}_N \C_n} \\[0.7em]
E[X] &= np \\[0.7em]
V[X] &= \frac{N-n}{N-1} np(1-p)
\end{align}
ただし,$p=M/N$であり,$\tilde{C}$は二項係数を拡張した記号である。
{}_N \tilde{C} _x &=
\begin{cases}
{}_N \C_x & (x=0,\cdots,n)\\[0.7em]
0 & (\text{その他})
\end{cases}
\end{align}
アタリが$M$個,ハズレが$N-M$個入っているくじ引きから$n$個を引くとき,アタリの個数$X$は超幾何分布に従います。超幾何分布に従う確率変数$X$に対し,実現値は
x \in \{0, \ldots, n\}
\end{align}
であり,確率母関数の変数は$|s|\leq 1$とします。超幾何分布は再生性を持たず,ロードマップ上では二項分布を非復元抽出として拡張した場合に相当します。なお,超幾何分布の確率母関数は計算が面倒なので割愛されることが多く,本稿もそれに従います。
確率質量関数
超幾何分布の確率質量関数は,高校数学の場合の数を利用して導かれます。アタリが$M$個,ハズレが$N-M$個入っているくじ引きから$n$個を引くとき,アタリの個数$X$は超幾何分布に従います。分母には,$N$個の中から$n$個選ぶ全事象が入ります。分子には,$M$個のアタリから$x$個選び,$N-M$個のはずれから$n-x$個選ぶ場合の数が入ります。結局,$x=0, \ldots, n$のとき,超幾何分布の確率質量変数は以下のように表されます。
f_{X}(x) &= \frac{{}_M \tilde{\C}_{x} \times {}_{N-M} \tilde{\C}_{n-x}}{{}_N \C_n}
\end{align}
ただし,$x$が赤玉の個数を上回ってしまう場合があるため,二項係数を拡張した${}_n \tilde{\C}_{x}$を導入しました。
{}_N \tilde{C} _x &=
\begin{cases}
{}_N \C_x & (x=0,\cdots,n)\\[0.7em]
0 & (\text{その他})
\end{cases}
\end{align}
確率母関数
超幾何分布の確率母関数は複雑なので割愛します。
平均・分散
超幾何分布の平均と分散を求める方法は2通りあります。
- $i$回目の試行に着目(おすすめ)
- 有限母集団から抽出した標本平均の期待値と分散を利用
- 期待値と分散の定義を愚直に計算
以下で説明しますが,超幾何分布の平均と分散を定義に沿って愚直に計算すると少し厄介ですので,ぜひこちらの「有限母集団から抽出した標本平均の期待値と分散」を利用する方法をおさえておいて下さい。
$i$回目の試行に着目
復元抽出とは異なり非復元抽出における場合の数は順番が無視できませんので,順列を用いて考えます。$N$個のくじから$n$個のくじを取り出し,左から並べ番号を付ける総数${}_{N}P_{n}$が全事象となります。一方,$i$番目のくじがアタリとなるのは$M$通りであり,残りの$N{-}1$個の球から$n{-}1$個のくじを取り出し,$i$番目を飛ばして左から番号を付ける総数は${}_{N-1}P_{n-1}$となります。したがって,
P(X_{i}=1)& \frac{M\cdot{}_{N-1}P_{n-1}}{{}_{N}P_{n}} =\frac{M}{N}\label{試行着目_1}
\end{align}
となります。同様に,$i$番目と$j$番目のくじがアタリとなるのは$M(M{-}1)$通りであり,残りの$N{-}2$個のくじから$n{-}2$個のくじを取り出し,$i$番目と$j$番目を飛ばして左から番号を付ける総数は${}_{N-2}P_{n-2}$となります。したがって,
P(X_{i}=1,X_{j}=1)& \frac{M(M-1)\cdot{}_{N-2}P_{n-2}}{{}_{N}P_{n}} =\frac{M(M-1)}{N(N-1)}\label{試行着目_2}
\end{align}
となります。
$X_{1}{=}1$となるのは$N$個の球のうち$M$個が選ばれる場合であり,求める確率は式($\ref{試行着目_1}$)のようになります。$X_{1}{=}1$かつ$X_{2}{=}1$となるのは$N$個の球のうち$M$個が選ばれ,続いて$N{-}1$個の球のうち$M{-}1$個が選ばれる場合であり,求める確率は式($\ref{試行着目_2}$)のようになります。このように,$i,j$番目に着目する確率と$1,2$番目に着目する確率は等しくなります。
すると,期待値の定義より,
E[X_{i}] &= 1\cdot P(X_{i}=1)+0\cdot P(X_{i}=1) = \frac{M}{N}
\end{align}
となります。同様に,
E[X_{i}^{2}] &= 1^{2}\cdot P(X_{i}=1)+0^{2}\cdot P(X_{i}=1) = \frac{M}{N}
\end{align}
となります。したがって,分散は
V[X_{i}] &= E[X_{i}^{2}]-E[X_{i}]^{2} = \frac{M}{N}-\left(\frac{M}{N}\right)^{2} = \frac{M(N-M)}{N^{2}}
\end{align}
となります。一方,係数が$0$である項を省略すると,
E[X_{i}X_{j}] &= 1^{2}\cdot P(X_{i}=1,X_{j}=1) = \frac{M(M-1)}{N(N-1)}
\end{align}
となるため,共分散は
\Cov[X_{i},X_{j}] &= E[X_{i}X_{j}]-E[X_{i}]E[X_{j}]
= \frac{M(M-1)}{N(N-1)}-\left(\frac{M}{N}\right)^{2} = -\frac{M(N-M)}{N^{2}(N-1)}
\end{align}
となります。以上を踏まえると,$X{=}X_{1}+\cdots+X_{n}$の期待値は
E[X] &= \sum_{i=1}^{n}E[X_{i}] = n\frac{M}{N} = np
\end{align}
となり,$X$の分散は
V[X] &= \sum_{i=1}^{n}V[X_{i}]+\sum_{i\neq j}\Cov[X_{i},X_{j}]\\[0.7em]
&= n\frac{M(N-M)}{N^{2}}-n(n-1)\frac{M(N-M)}{N^{2}(N-1)}\\[0.7em]
&= \frac{nM(N-M)(N-1)-n(n-1)M(N-M)}{N^{2}(N-1)}\\[0.7em]
&= \frac{M(N-M)\{n(N-1)-n(n-1)\}}{N^{2}(N-1)}\\[0.7em]
&= \frac{M(N-M)\{n(N-n)\}}{N^{2}(N-1)}\\[0.7em]
&= \frac{N-n}{N-1}\cdot n\cdot \frac{M}{N}\cdot \left(1-\frac{M}{N}\right)
= \frac{N-n}{N-1}np(1-p)
\end{align}
となります。ただし,$i\neq j$となる総数は,$n$個のインデックスから$(i,j)$の選び方として${}_{n}C_{2}$通り,$(i,j)$の並べ方として$2$通りで,結局$n(n-1)$通りとなることを利用しています。
有限母集団から抽出した標本平均を利用
有限母集団における標本平均の期待値と分散で説明した通り,有限母集団から抽出した標本平均の期待値と分散は以下のように表されます。
E[\overline{X}] &= \mu \\[0.7em]
V[\overline{X}] &= \frac{N-n}{N-1}\frac{\sigma^2}{n}
\end{align}
ただし,有限母集団の母平均を$\mu$,母分散を$\sigma^2$とおきました。この結果を利用しましょう。いま,大きさ$N$の有限母集団を考え,特性値(観測される値)を
a_1 &= \cdots &&= a_M &&= 1 \\[0.7em]
a_{M+1} &= \cdots &&= a_N &&= 0
\end{alignat}
とおきます。ただし,特性値が$1$であることをアタリとしました。この母集団から大きさ$n$の非復元抽出を行うとき,以下の確率変数
X &= X_1 + \cdots + X_n \\[0.7em]
&= n \overline{X}
\end{align}
が従う分布が超幾何分布になります。なぜなら,アタリが$M$個,ハズレが$N-M$個入っているくじ引きから$n$個を引くとき,アタリの個数は超幾何分布に従うからです。
さて,ここからは$E[X]$と$V[X]$を求めることが目標です。しかし,現段階では$\mu$と$\sigma^2$が分かっていないため,$E[X]$と$V[X]$を求めることができません。そこで,改めて$\mu$と$\sigma^2$の定義を確認しておきましょう。有限母集団の母平均と母分散の定義より,$\mu$と$\sigma^2$は以下のように定義されます。
\mu &= E[X_1] \\[0.7em]
\sigma^2 &= V[X_1]
\end{align}
ただし,有限母集団から$1$個の観測値を無作為抽出した確率変数を$X_1$とおきました。
そこで,ここからは$E[X_1]$と$V[X_1]$を求めることが目標になりました。アタリが$M$個,ハズレが$N-M$個入っている有限母集団から無作為に$1$個の観測値$X_1$を抽出するとき,$X_1$が$1$である確率は$M/N$ですので,$X_1$はパラメータ$p=M/N$のベルヌーイ分布に従っていることになります。したがって,$E[X_1]$と$V[X_1]$は以下のように表されます。
E[X_1] &= p \\[0.7em]
V[X_1] &= p(1-p)
\end{align}
さて,ここで有限母集団から抽出した標本平均の期待値と分散の定理を利用します。すなわち,有限母集団から抽出された観測値の標本平均の期待値は母平均と変わらず,分散は無限母集団の場合の結果に対して有限修正項を付け加えた結果となります。したがって,超幾何分布の平均と分散は ,以下のように表されます。
E[X] &= nE[\overline{X}] \\[0.7em]
&= n\mu \\[0.7em]
&= np \\[0.7em]
V[X] &= n^2 V[\overline{X}] \\[0.7em]
&= n^2\frac{N-n}{N-1}\frac{\sigma^2}{n} \\[0.7em]
&= \frac{N-n}{N-1}np(1-p)
\end{align}
「無作為に$1$個の観測値$X_1$を抽出するとき」で少し違和感を覚える方がいるかもしれません。自分も例外ではなく,「なぜ$1$回の抽出に注目するだけでよいのか」という部分で引っかかりました。実際に非復元抽出しているのは$n$個のはずなのに,最初の$1$回だけに着目してベルヌーイ試行とみなすのは「非復元抽出とは言えないのではないか」と思っていました。この疑問に対する答えは,上でも同様のことを述べていますが,「非復元抽出という意味合いは有限修正項によって付け加えられる」というものです。そもそも,母平均$\mu$の定義が$E[X_1]$であり,有限母集団から無作為に抽出された$1$回の観測値に関する期待値を表しています。母分散も同様に,$1$回の観測値に関する分散を表しています。有限修正項は,$1$回の無作為抽出に対して,有限母集団からの非復元抽出という意味合いを付け加えるために利用される概念です。$E[X_1]$の定義自体が,$1$回の無作為抽出に関する結果を表していることに注意してください。$2$回以上の試行を考慮したいのであれば,確率変数を条件付ける必要があります。例えば,$E[X_2|X_1]$は$1$回目の試行の結果を踏まえたうえでの$2$回目の試行の期待値を表しています。
期待値と分散の定義を愚直に計算
通常,離散分布の平均と分散を求める際には「確率母関数の性質」を利用します。しかし,超幾何分布の確率母関数は複雑であるため,平均と分散を求める際は定義を利用します。
新しく導入した二項係数に関して重要な性質を利用します。
{}_N \C_{n} &= \sum_{x=1}^n {}_M\tilde{\C}_{x} \times {}_{N-M}\tilde{\C}_{n-x}\label{equation:拡張二項係数の性質}
\end{align}
この等式の意味は,左辺は$N$個のくじから$n$本を引くという場合の数で,右辺はそれをアタリの本数$x$による場合わけでカウントしています。つまり,全てのアタリの本数$M$から$x$本引く場合と,ハズレから残りを引く場合を考えているだけです。さて,まずは平均から計算していきます。ポイントは,分子の掛け算のうち右側の項は変わらないということです。
E[X] &=
\sum_{x=0}^n x\cdot P(X=x)\\[0.7em]
&= \sum_{x=0}^n \frac{x\cdot {}_M\tilde{\C}_{x} \times {}_{N-M}\tilde{\C}_{n-x}}{{}_N \C_{n}}\\[0.7em]
&= \sum_{x=0}^n \frac{M\cdot {}_{M-1}\tilde{\C}_{x-1} \times {}_{N-M}\tilde{\C}_{n-x}}{{}_N \C_{n}}&\quad&(\because\text{二項係数の定義より})\\[0.7em]
&= \sum_{x=0}^n \frac{M\cdot {}_{M-1}\tilde{\C}_{x-1} \times {}_{N-M}\tilde{\C}_{n-x}}{(N/n)\cdot{}_{N-1} \C_{n-1}}&\quad&(\because\text{二項係数の定義より})\\[0.7em]
&= \frac{nM}{N}\sum_{x=0}^n \frac{{}_{M-1}\tilde{\C}_{x-1} \times {}_{N-M}\tilde{\C}_{n-x}}{{}_{N-1} \C_{n-1}}&\quad&(\because\text{ただの式変形})\\[0.7em]
&= \frac{nM}{N}\sum_{x=0}^n \frac{{}_{M-1}\tilde{\C}_{x-1} \times {}_{(N-1)-(M-1)}\tilde{\C}_{(n-1)-(x-1)}}{{}_{N-1} \C_{n-1}}&\quad&(\because\text{ただの式変形})\\[0.7em]
&= \frac{nM}{N}\cdot\frac{{}_{N-1} \C_{n-1}}{{}_{N-1} \C_{n-1}}&\quad&(\because\text{式(\ref{equation:拡張二項係数の性質})より})\\[0.7em]
&= n\frac{M}{N} \\[0.7em]
&= np
\end{alignat}
ただし,$p=M/N$とおきました。続いて,分散を計算していきます。基本的には平均と同じ方針で計算することができるのですが,二項係数に「階乗」の形が複数含まれていることから,計算を簡単にするために$E[X^2]$ではなく$E[X(X-1)]$を考えることにします。そうです。確率母関数から分散を求めるときと同じアイディアです。
V[X] &= E[X^2]-E[X]^2\\[0.7em]
&= E[X(X-1)] + E[X]-E[X]^2
\end{align}
$E[X]$はすでに求められていますので,以下では$E[X(X-1)]$を計算していきます。途中まで先ほどと同様の計算が現れます。ポイントも先ほどと同じで,分子の掛け算のうち右側の項は変わらないということです。
E[X(X-1)] &=
\sum_{x=0}^n x(x-1)\cdot P(X=x)\\[0.7em]
&= \frac{nM}{N}\sum_{x=0}^n \frac{(x-1)\cdot{}_{M-1}\tilde{\C}_{x-1} \times {}_{(N-1)-(M-1)}\tilde{\C}_{(n-1)-(x-1)}}{{}_{N-1} \C_{n-1}}\\[0.7em]
&= \frac{nM}{N}\sum_{x=0}^n \frac{(M-1)\cdot{}_{M-2}\tilde{\C}_{x-2} \times {}_{(N-2)-(M-2)}\tilde{\C}_{(n-2)-(x-2)}}{\left\{(N-1) / (n-1) \right\}{}_{N-2} \C_{n-2}}\\[0.7em]
&= \frac{n(n-1)M(M-1)}{N(N-1)}\sum_{x=0}^n \frac{{}_{M-2}\tilde{\C}_{x-2} \times {}_{(N-2)-(M-2)}\tilde{\C}_{(n-2)-(x-2)}}{{}_{N-2} \C_{n-2}}\\[0.7em]
&= \frac{n(n-1)M(M-1)}{N(N-1)}\cdot\frac{{}_{N-2} \C_{n-2}}{{}_{N-2} \C_{n-2}}\\[0.7em]
&= \frac{n(n-1)M(M-1)}{N(N-1)}
\end{align}
したがって,分散は以下のように計算できます。
V[X] &= E[X(X-1)] + E[X]-E[X]^2\\[0.7em]
&= \frac{n(n-1)M(M-1)}{N(N-1)} + \frac{nM}{N}-\left(\frac{nM}{N} \right)^2\\[0.7em]
&= \frac{nM}{N^2} \left\{ \frac{(N-n)(N-M)}{N-1} \right\} \\[0.7em]
&= \frac{N-n}{N-1} n\frac{M}{N}\left(1-\frac{M}{N}\right)\\[0.7em]
&= \frac{N-n}{N-1}np(1-p)
\end{align}
再生性
再生性を示すためには,再生性を示したい分布に従う独立な二つの確率変数を考え,その和の確率母関数を計算したときに,パラメータが和の形になっていることを示します。超幾何分布の確率母関数は複雑な形をしており,和の確率母関数を考えてもパラメータが和の形にはならないため,超幾何分布は再生性を持ちません。
ロードマップ
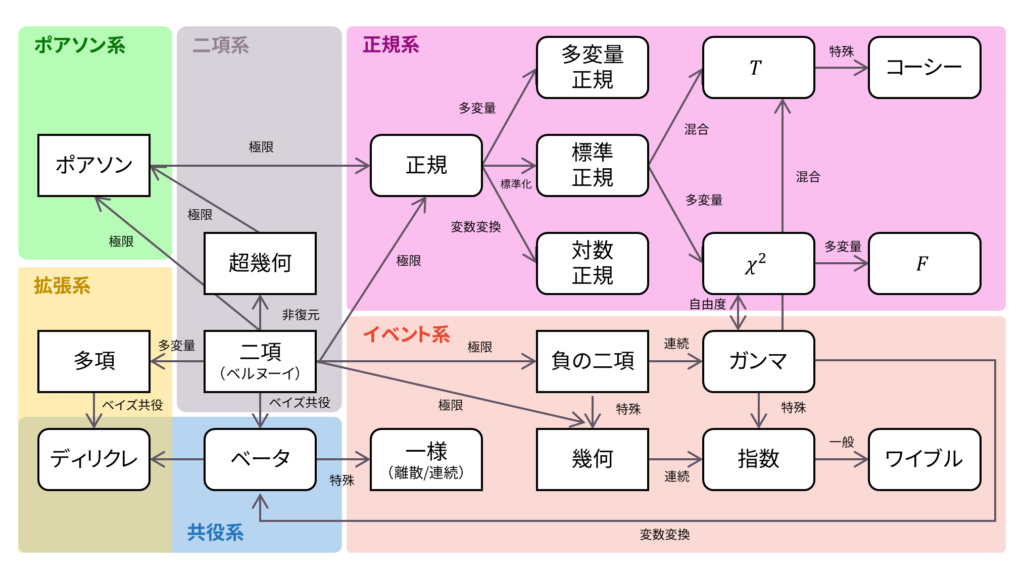
さて,ロードマップに戻りましょう。超幾何分布は,二項分布の非復元拡張として導入されました。以下の内容も参考になるでしょう。
参考文献
本稿の執筆にあたり参考にした文献は,以下でリストアップしております。


コメント