統計検定1級の過去問解答解説を行います。目次は以下をご覧ください。
不適切な内容があれば,記事下のコメント欄またはお問い合わせフォームよりご連絡下さい。
問題
統計検定1級の過去問からの出題になります。統計検定の問題の著作権は日本統計学会に帰属していますので,本稿にて記載することはできません。「演習問題を俯瞰する」で詳しく紹介している公式の過去問題集をご購入いただきますようお願い致します。
解答
経験分布と混合分布に関する出題でした。
(1)
経験分布$F(x)$は,$x$以下となる観測値の割合
F(x) &= \frac{1}{n}(X_{i}\leq x となる i の数)
\end{align}
で定義される。したがって,求める答えは下図の通りである。
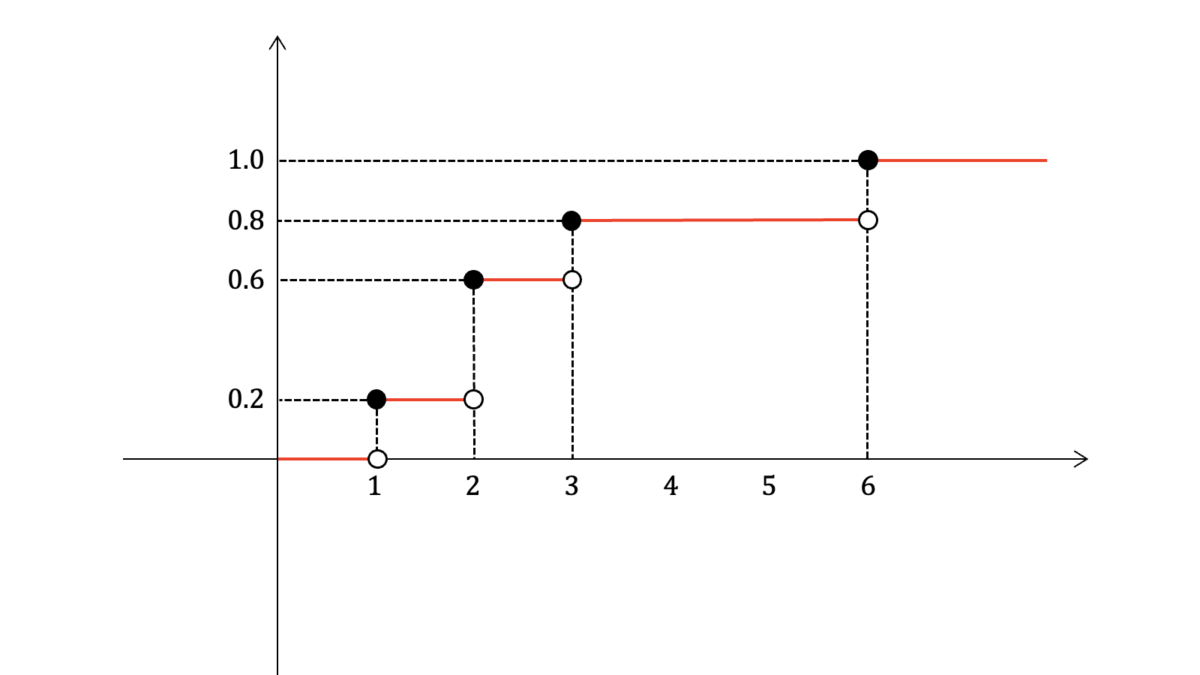
(2)
標本平均は
(1\times 0.2)+(2\times 0.4)+(3\times 0.2)+(4\times 0.2)
\end{align}
であるが,各項を
(横の長さ)\times (縦の長さ)
\end{align}
と捉えると,横長の長方形が縦に積み重なった下図の色付き部分が標本平均に相当する。
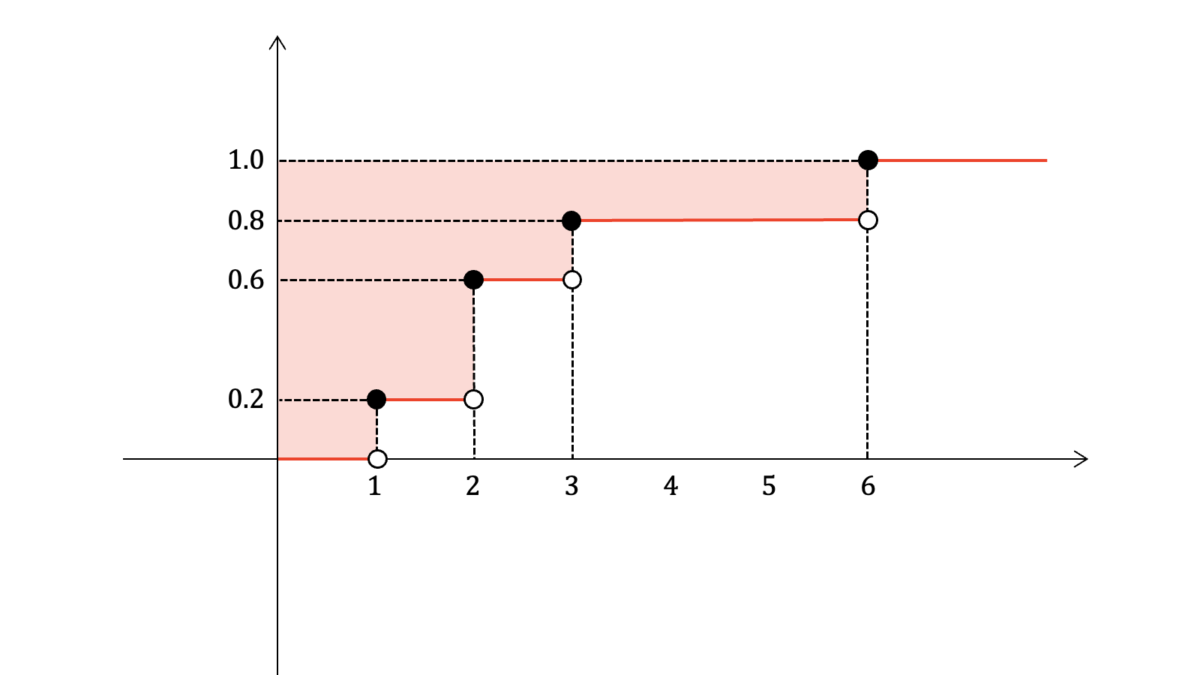
(3)
累積分布関数の定義より,
\int_{0}^{\infty}\{1-F(x)\}dx
&= \int_{0}^{\infty}\left(\int_{x}^{\infty}f(y)dy\right)dx
\end{align}
となる。積分領域は$0\leq x < \infty$,$x\leq y < \infty$であるが,これは$0\leq y < \infty$,$0\leq x \leq y$と等価である。
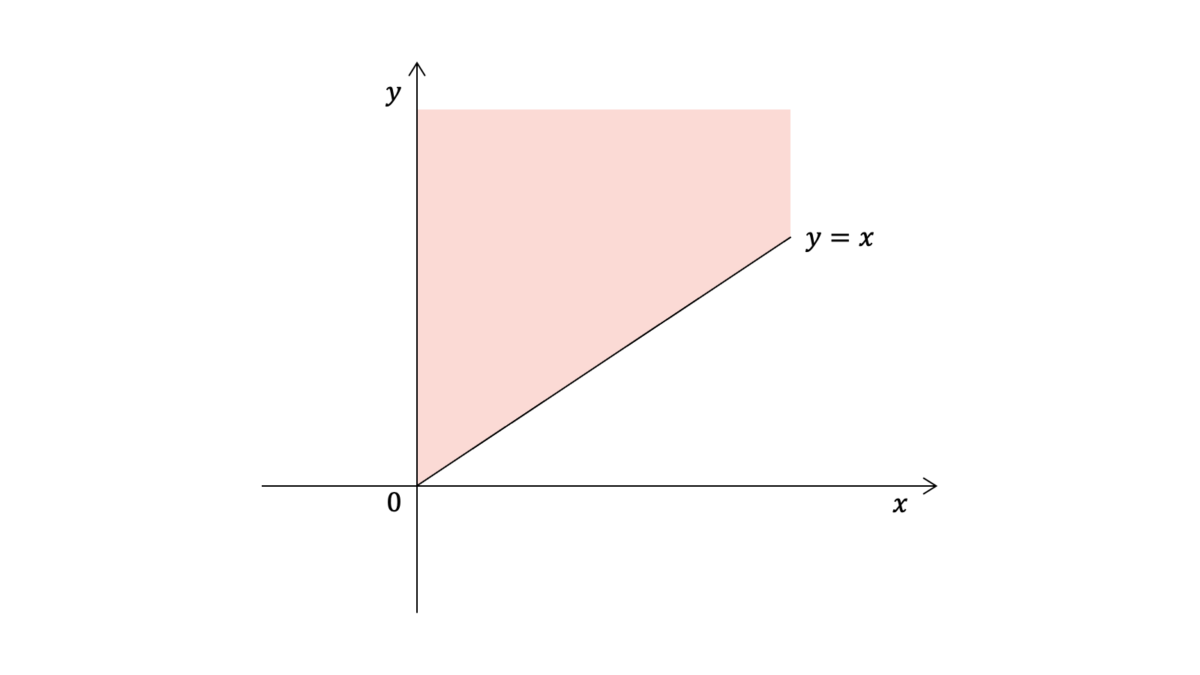
したがって,
\int_{0}^{\infty}\left(\int_{x}^{\infty}f(y)dy\right)dx
&= \int_{0}^{\infty}\left(\int_{0}^{y}f(y)dx\right)dy
= \int_{0}^{\infty}f(y)\left(\int_{0}^{y}dx\right)dy\\[0.7em]
&= \int_{0}^{\infty}yf(y)dy
= \int_{0}^{\infty}xf(x)dx
= E[X]
\end{align}
が成り立つ。
(3)の結果は(2)の図を裏付けています。$1$から経験分布関数の値を引いた値が標本平均になります。
(4)
与えられた混合分布の定義より,
f(x)
&= \int_{0}^{\infty}\lambda e^{-\lambda x}\cdot \frac{\beta^{\alpha}}{\Gamma(\alpha)}\lambda^{\alpha-1}e^{-\beta\lambda}d\lambda\\[0.7em]
&= \frac{\beta^{\alpha}}{\Gamma(\alpha)}\int_{0}^{\infty}\lambda^{\alpha}e^{-(\beta+x)\lambda}d\lambda
\end{align}
と変形できる。ここで,
\lambda^{\alpha}e^{-(\beta+x)\lambda}
\end{align}
は$\alpha^{\prime}=\alpha+1$,$\beta^{\prime}=\beta+x$のガンマ分布の形をしているから,定数項が付いていないことに注意すると
\int_{0}^{\infty}\lambda^{\alpha}e^{-(\beta+x)\lambda}d\lambda
&= \frac{\Gamma(\alpha^{\prime})}{(\beta^{\prime})^{\alpha^{\prime}}}
= \frac{\Gamma(\alpha+1)}{(\beta+x)^{\alpha+1}}
\end{align}
となる。したがって,
f(x)
&= \frac{\beta^{\alpha}}{\Gamma(\alpha)}\frac{\Gamma(\alpha+1)}{(\beta+x)^{\alpha+1}}
= \frac{\alpha\beta^{\alpha}}{(\beta+x)^{\alpha+1}}
\end{align}
が得られる。ただし,$x$の範囲は$g(x)$によって定義されている$x\geq 0$である。
(5)
(4)より,$f(x)$の累積分布関数は
F(x)
&= \int_{0}^{x}\frac{\alpha\beta^{\alpha}}{(t+\beta)^{\alpha+1}}dt
= \alpha\beta^{\alpha}\int_{0}^{x}(t+\beta)^{-\alpha-1}dt\\[0.7em]
&= \alpha\beta^{\alpha}\left[-\alpha^{-1}(t+\beta)^{-\alpha}\right]_{0}^{x}
= 1-\left(\frac{\beta}{\beta+x}\right)^{\alpha}
\end{align}
となる。ただし,$x\geq 0$である。したがって,(3)より,
E[X]
&= \int_{0}^{\infty}\{1-F(x)\}dx
= \int_{0}^{\infty}\left(\frac{\beta}{\beta+x}\right)^{\alpha}dx\\[0.7em]
&= \beta^{\alpha}\int_{0}^{\infty}(\beta+x)^{-\alpha}dx
= \beta^{\alpha}\left[(-\alpha+1)^{-1}(\beta+x)^{-\alpha+1}\right]_{0}^{\infty}
\end{align}
が得られる。$E[X]$は収束するためには$-\alpha+1<0$となるため,求める条件は$1<\alpha$である。このとき,
E[X]
&= \frac{\beta}{\alpha-1}
\end{align}
となる。
別解
(3)の結果を使わずとも,期待値の定義から求めることもできます。$1<\alpha$のとき,
E[X]
&= \int_{0}^{\infty}x\frac{\alpha\beta^{\alpha}}{(\beta+x)^{\alpha+1}}dx\\[0.7em]
&= \int_{0}^{\infty}(\beta+x-\beta)\frac{\alpha\beta^{\alpha}}{(\beta+x)^{\alpha+1}}dx\\[0.7em]
&= \int_{0}^{\infty}\frac{\alpha\beta^{\alpha}}{(\beta+x)^{\alpha}}dx-\int_{0}^{\infty}\frac{\alpha\beta^{\alpha+1}}{(\beta+x)^{\alpha+1}}dx\\[0.7em]
&= \frac{\alpha\beta}{\alpha-1}-\frac{\alpha\beta}{\alpha}
= \frac{\alpha\beta}{\alpha(\alpha-1)}
= \frac{\beta}{\alpha-1}
\end{align}
と計算できます。


コメント